多圆柱体浮标的横摇性能分析

魏晓辉 ，尼建军 ，李宏武 ，刘 宁 *，董 涛

（1. 国家海洋技术中心，天津 300112； 2. 海军装备部驻天津地区第一军事代表室，天津 300131）

波浪测量浮标是观测和收集海浪数据的重要手段之一，在海洋事业各个领域应用广泛[1]。但对于研究一些极端海况，人为投放浮标会极大地增加作业的危险性，因此，利用无人机运输投放浮标，不仅可以减小作业的危险性，还可以快速到达目标海域进行海浪测量。为了适应无人机吊舱的外形，需要设计一种投弃式圆柱体浮标，同时浮标要有较小的横摇角度，降低天线束宽的要求，提高天线增益，增加系统的通信质量[2-3]。

目前，无论基于加速度传感器还是GPS，目前波浪测量浮标大多为球体浮标，直径约为0.5～1.0 m，如表1 所示。虽然球体浮标拥有较好的横摇性，但无法被无人机搭载，而细长形的圆柱浮标则有较差的横摇性能，容易在恶劣海况下被海浪打翻，因此空投波浪测量浮标需要在保持圆柱体的前提下，增强其横摇性能。本文通过分析不同直径和径高比圆柱体浮标的横摇性能，设计了一种多圆柱体的浮标，该浮标中的较大直径的圆柱可以折叠，减小浮标整体径向长度，以适应无人机的吊舱。

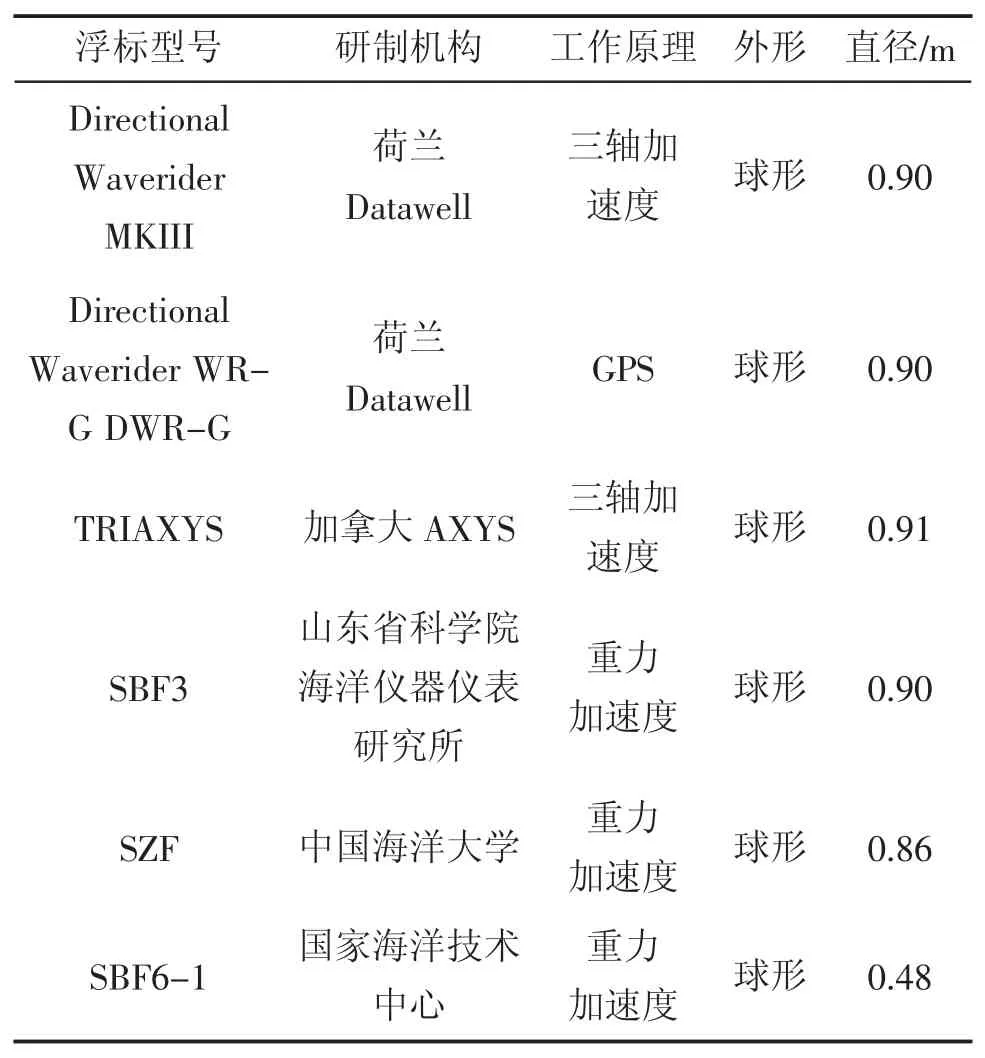
表1 国内外波浪测量浮标工作原理及外形[4-7]

1 浮标的横摇运动理论

1.1 浮标的横摇周期

浮标在静水中作横摇运动的固有圆频率ωφ为[8]：

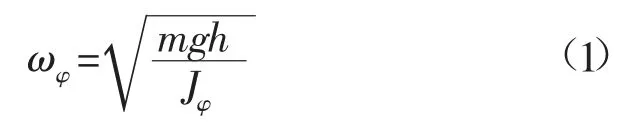
式中：m为浮标的质量；g为重力加速度；h为初稳心高；Jφ为转动惯量。转动惯量Jφ包括整个浮标绕水线面的中心轴的转动惯量J和附加质量引起的转动惯量J＇。实际情况中，横摇阻尼很小，对横摇固有圆频率的影响可以忽略，故式（1）中未考虑阻尼，由此可知，浮标的固有圆频率仅与浮标的质量、初稳心高和转动惯量有关。

在横倾角dφ 不大时，浮心的运动轨迹可以看作是以初稳心为圆心，做小角度的圆轨运行，同时，稳心的位置可以近似看作不变。因此，浮标的恢复力矩为：

式中：h为初稳心高；a为重心和浮心的距离，即a=│Zg-Zb│；Vw为排出水的体积；ρw为海水的密度。

当浮标倾斜且倾角不大时，可看作浮标竖直水线倾斜，此时，产生浮力为楔形体积的排水量，浮心的改变也是由楔形体积排水量不对称所引起的，因而可以求得浮标恢复力矩的另一种形式[9]：

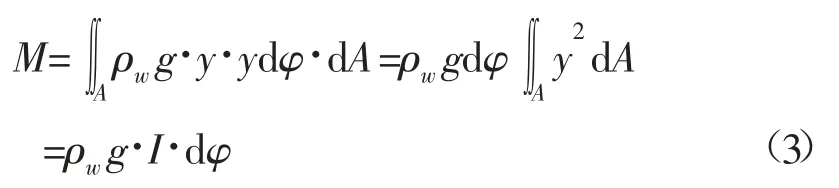
式中：dA为楔形体积水线面A上的微元面积；y为微元面积至水线面上转动中心线的距离；I为水线面对于转动中心线的惯性矩；g为重力加速度。式（1）与式（2）联立可得：

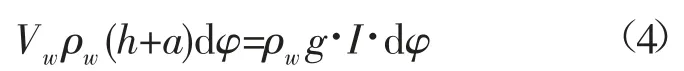
因此，浮标的初稳心高为：

根据实践经验，浮标的总转动惯量可以通过杜埃尔公式估算，浮标的转动惯量为[10-11]：

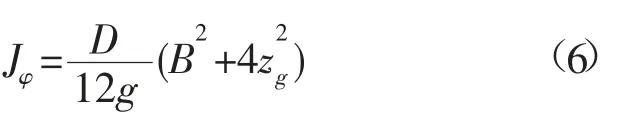
式中：D为浮标排水量；B为浮标的直径；zg为浮标重心到基线的高度。当初稳心高h＞0.15 m 时，浮标的固有周期为：

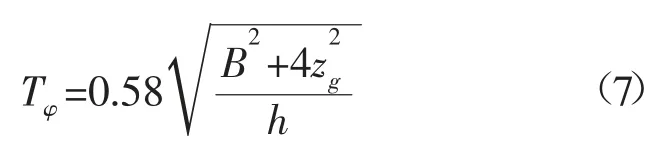
当时，浮标的固有周期为：

式中：φmax为最大横摇角；r为横稳心半径。

当 0.05＜h＜0.15 时，浮标的固有周期为式（7）和式（8）计算结果的平均值。

1.2 浮标在规则波中的横摇运动

浮标在规则波中的横摇运动如图1 所示。

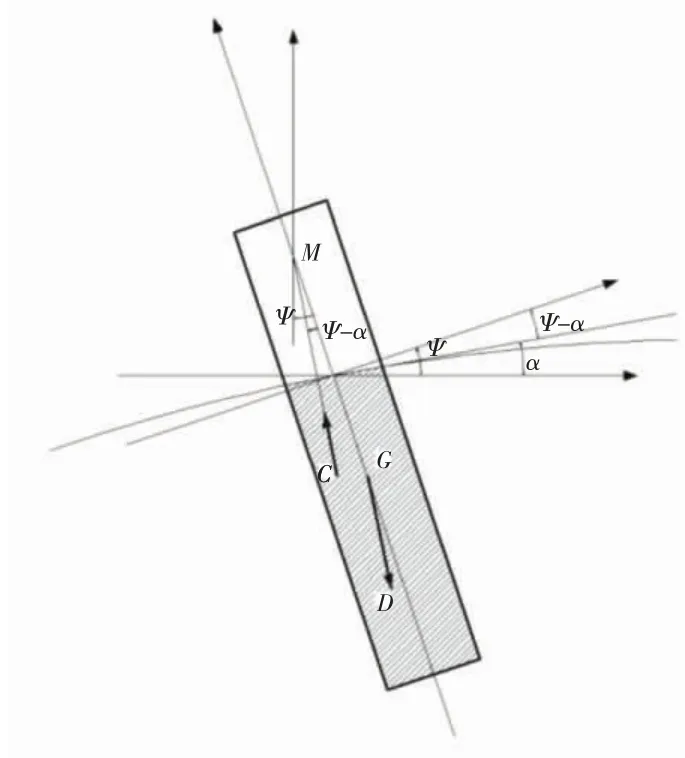
图1 浮标在规则波中的横摇

根据横摇经典理论[12]，在无阻尼状态下，浮标的横摇方程为：

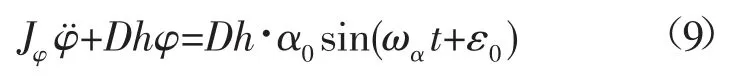
式中：α0为波浪的倾角的幅值；ωα为波浪的圆频率；ε0为波浪角与浮标倾角的初相位差。假设初始条件则式（9）的解为：

式中：Tφ和Tα分别为浮标横摇的固有周期和波浪的周期。

引入横摇的放大因子K=φmax/α0，则K可表示为：

2 圆柱体浮标与球体浮标横摇性能分析

2.1 圆柱体浮标横摇性能分析

假设圆柱体浮标的直径为d，高度为hc，则径高比k=d/hc，密度为750 kg/m3，重心位于浮标的0.25hc处，故重心至水线面的距离zg=0.5hc，浮心至水线面的距离zb=0.385hc。因此，圆柱体浮标的初稳心高为：

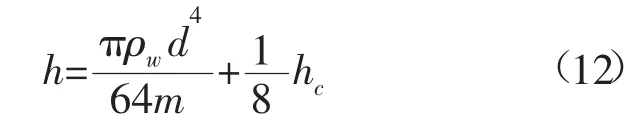
将式（12）代入式（7）可得圆柱体浮标的固有周期为：

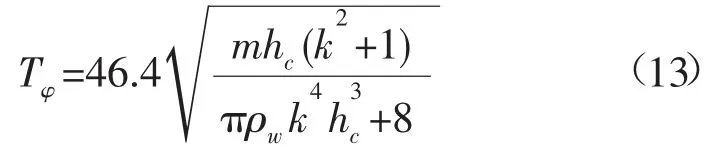
设定波浪的周期Tα=4s，则放大因子K为：

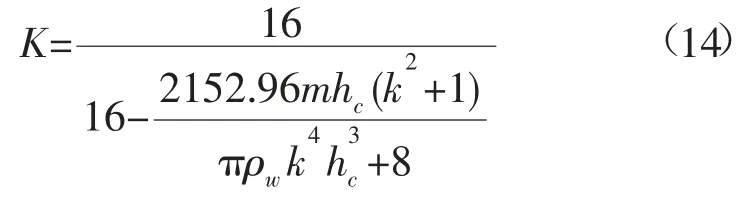
由式（14）可知，在浮标质量确定的情况下，圆柱体浮标的横摇性能仅与高度和径高比有关。分别计算当hc=0.5 m，0.15 m，0.25 m，0.35 m，0.45 m，0.55 m，0.65 m，0.75 m 时，k从 0 到 10 的放大因子，计算结果如图2 所示。

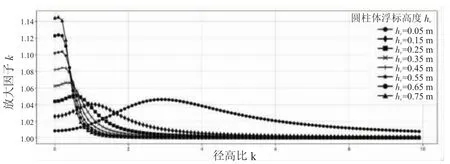
图2 不同高度的圆柱体浮标横摇性能随径高比的变化

由图2 可知，随着径高比增大，圆柱体浮标横摇运动的放大因子先增大后减小，最终趋向于1，即随波漂流；而随着直径的增大，放大因子的峰值变大，并向左移动。当浮标高度大于0.25 m 时，放大因子在径高比为4 处就已达到平稳状态，因此，在设计圆柱形浮标时，尽量选择较高径高比，避开峰值区域。

2.2 球体浮标横摇性能分析

假设球体浮标的直径为d，密度为750 kg/m3，重心位于浮标的0.25d处，故重心至水线面的距离zg=0.403d，浮心至水线面的距离zb=0.25d。因此，圆柱体浮标的初稳心高为：

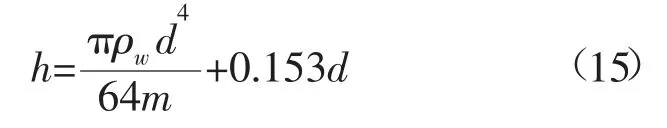
通过式（7）、式（11）和式（15），可以计算得到球形浮标的放大因子随直径的变化趋势，设定波浪周期Tα=4 s，计算结果如图 3 所示。

图3 球体浮标横摇性能随直径的变化

由图3 可见，球体浮标的放大因子均低于1.03，横摇性能优良。对于目前的大部分球体波浪测量浮标，直径约为0.5～1.0 m，既保证体积不会很大，又有良好的横摇性能，如果直径继续增大，放大因子减小不明显，横摇性能并不会明显提高。

3 多圆柱体浮标横摇性能分析

由于无人机吊舱的尺寸限制，用于空投的波浪测量浮标的直径要求小于0.124 m，通过图2 可知，只有径高比大于4 时，才有较好的横摇性能，即高度只有0.03 m，实际上是不可行的。因此，需要设计一个径向可折叠的圆柱体，投放后展开以增大浮标的径高比，如图4 所示。底部圆柱体的直径为0.09 m，径高比为0.18，上部圆柱体直径为0.9 m，径高比为30，通过布置内部配重模块，使水线面位于上部圆柱体的底面偏上0.01 m 处的位置，重心位于下部圆柱体。

图4 多圆柱体浮标结构示意图

海浪被视为为一种随机过程，在风和地形的影响下，海浪的变化是极其复杂的，经典的线性理论无法阐明其特征，故采用频谱对海浪进行描述和预测。在各种海浪频谱中，常用的由Pierson-Moscowitz（P-M）谱和JONSWAP 谱。其中P-M 谱是将北大西洋上已观察的54 个充分成长的海浪，按照风速分为5 组，就各组的谱求一平均谱，然后将这些谱无因次化，并以不同形式的无因次谱进行拟合，最后得到的有因次谱[13]：

式中：无因次常数 α=8.10×10-3；β=0.74；U为海面上19.5 m 高度处的风速。各级海况的平均风速、平均波高和周期如表2 所示[14]。

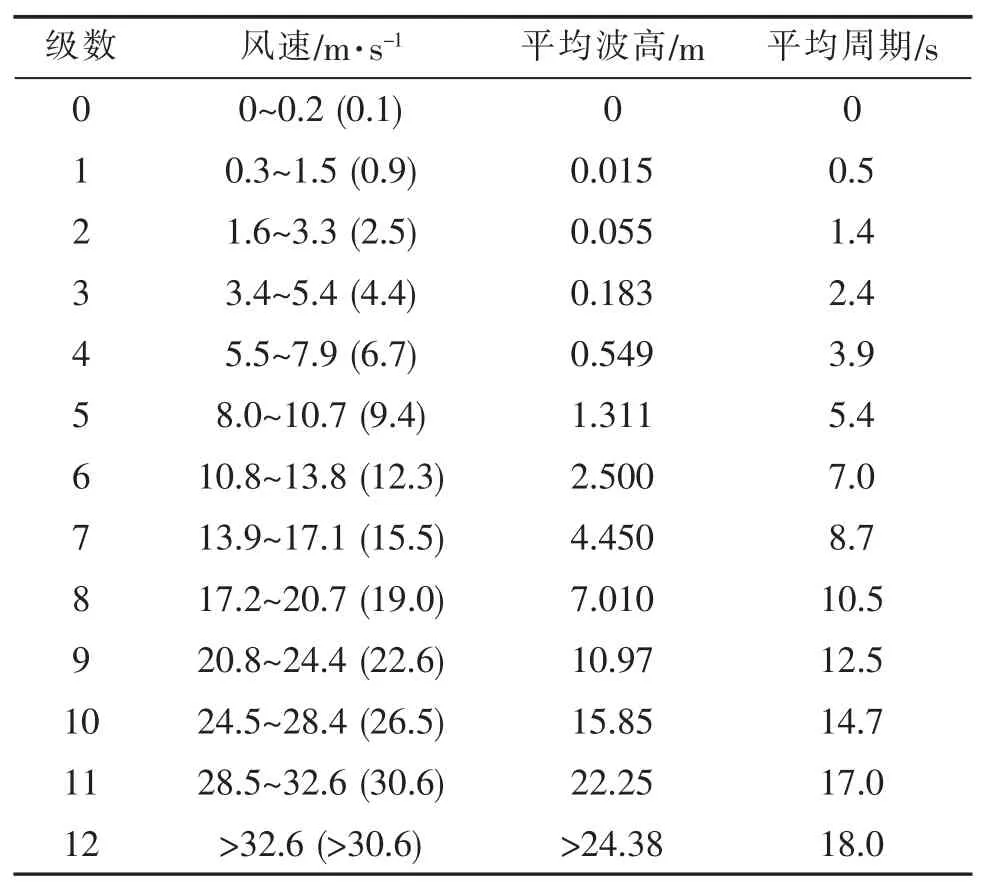
表2 海况等级

为了能够分析实海况条件下多圆柱体浮标的横摇性能，选择表2 中5 级海况下的风速，并假定海水是无旋、无粘的。浮标的横摇运动计算结果，如图5所示。利用Python 绘制浮标的横摇角度随时间的变化图[15]，结果如图 6 所示。

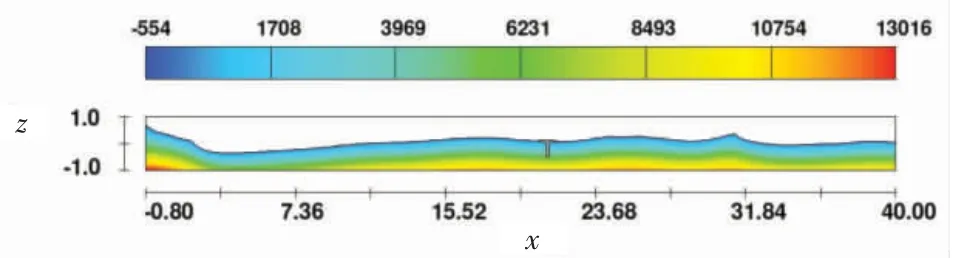
图5 多圆柱体横摇运动仿真

图6 多圆柱体浮标的横摇角度

由图6 可知，在5 级海况下，依据图2 设计的多圆柱体浮标的最大横摇角度小于20°，小于设计要求的30°，说明该形状浮标的横摇性能良好。

4 多圆柱体空投浮标设计与试验

浮标主体结构（下层圆柱体）采用厚度为2 mm的3A21 铝合金圆筒，根据经验这种结构可以满足安全入水的要求，另外3A21 铝合金既可以焊接，也有较好的抗腐蚀性能，还不具有磁性，同时，它的密度比不锈钢、钛合金等材料低。减速板（上层圆柱体）径高比45，是由8 根主梁和544 航空伞布制成，其中主梁是由玻璃微珠复合材料加工制成，密度仅为500 kg/m3，能够极大地增加浮标的储备浮力，提高稳定性。浮标顶部采用ABS 塑料制成，以确保对卫星通讯没有电磁屏蔽，便于数据接收和发送。浮标总长0.887 m，减速板闭合状态时最大直径为0.124 m，展开状态时最大直径为0.89 m，符合无人机搭载要求。

浮标由4 部分组成，从上到下依次为：天线舱、电路模块舱、电池舱和减速板及其启动装置模块。天线舱内部装有北斗卫星天线、陀螺仪、加速度传感器、数据处理电路和北斗天线电路装于电路模块舱，电池舱与电路模块舱通过转接环连接，电池舱的下部是减速板的启动模块，内置304 不锈钢配重块，可根据使用环境配重块的质量，从而改变浮标的重心位置，减速板覆盖于电路模块舱和电池舱表面，如图7 所示。浮标的每个模块舱均为独立结构，通过螺纹与拉杆连接，浮标体表面无螺钉，防止储存和工作过程中发生电化学腐蚀。

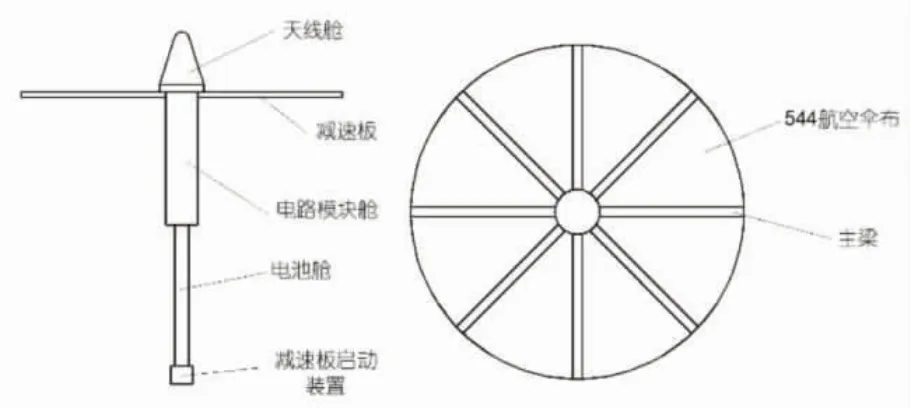
图7 浮标总体布置及外形

为了测试多圆柱体浮标在真实海况中的工作情况，验证浮标的横摇性能在不规则波中是否符合要求，在青岛附近海域进行海上试验，选取海浪较大的区域投放，同时在附近投放国家海洋技术中心研制的SBF7-1 型波浪浮标，记录此区域的波浪参数。

SBF7-1 型波浪浮标为球形锚定式浮标，而空投浮标为投弃式浮标，因此放置SBF7-1 型波浪浮标后，在其3 km 内投放空投浮标，并保持100 m 左右的距离跟随浮标，防止漂远。空投浮标和SBF7-1型波浪浮标的海上漂浮状态分别如图8 和图9 所示。

图8 空投波浪测量浮标漂浮状态

图9 SBF7-1 型波浪浮标漂浮状态

SBF7-1 型波浪浮标测量得试验过程中海浪的有效波高为1.1 m，接近5 级海况。空投浮标的横摇角度通过内置的陀螺仪收集，由于浮标在随机海浪中存在旋转运动，故不规定浮标横摇的方向，计算在各个方向浮标轴线与垂线之间的夹角，记为浮标的倾角，如图10 所示。

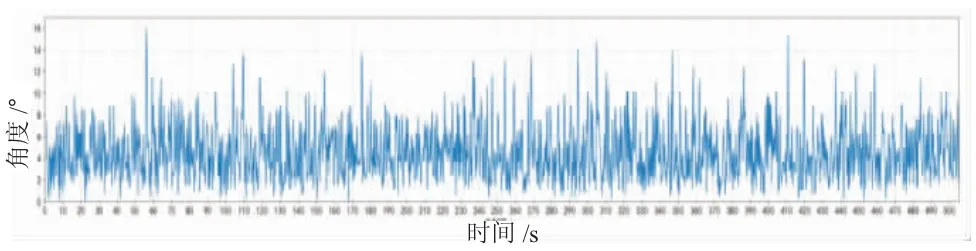
图10 空投波浪测量浮标漂浮状态

由图10 可知，浮标的横摇倾角最大约为16°，与计算模拟结果相似，说明多圆柱体浮标具有较好的横摇性能。

5 结论

本文阐述了浮标横摇运动理论，在此基础上分析圆柱体浮标和球体浮标横摇性能与特征尺寸的关系，根据分析结果设计一种能够被无人机搭载的多圆柱体浮标，计算了该浮标在5 级海况下的横摇角度，数值模拟结果符合设计要求。另外，本文还介绍了空投浮标的布局与结构，完成了海上试验，结果表明浮标在有效波高为1.1 m 的海浪中的横摇倾角最大约为16°。结合计算结果得到以下结论：

（1）圆柱体浮标的横摇特性随径高比增大而先增大后减小，球体浮标的横摇特性随直径的增大而先增大后减小，分析结果能够为浮标外形和尺度的确定提供依据，为浮标的设计提供理论基础。

（2）采用多圆柱体结构设计可以弥补圆柱体浮标横摇性能差的缺点，但要求上部圆柱体的径高比较大。

（3）多圆柱体浮标在5 级海况下的横摇角度小于30°，能够保证较高的卫星通讯质量。