基于高阶累积量的简正波声场匹配场定位效果分析

厉彦一，施 剑，罗 宇，徐 辉

（山东科技大学 测绘科学与工程学院，山东 青岛 266590）

匹配场声源定位（Matched Field Processing，MFP）是在已获取水听器信号和已知声场模型的基础上反演声源位置的一种技术。匹配场处理理论的奠基人M J Hinich 等[1]提出，在海平面下构造垂直阵列，然后进行海洋环境中信源的定位，从理论上推导出模式幅度系数和描述声源深度的最大似然方程，并在之后提出了Cramer-Rao 界并将其下限拓展到对声源距离的估计中[2]。H P Bucker[3]构造了一个可视为空间匹配滤波器的估计器，引入模糊表面的概念，借此描述拷贝场和接收信号之间匹配程度，并证明波场具有足量的信息，这些信息足以进行匹配场定位和匹配场信道参数反演，这对匹配场的发展有重大意义。在理论上符合高斯分布的接收信号中，所需要的信息都可直接在信号的低阶统计量找到对应的描述，但并非所有信号都能完美地符合高斯分布[4]。因此想要具体描述非高斯过程信号，需运用接收信号的高阶统计量。由于高阶累积量不同于高阶矩的性质，出现了大量应用高阶累积量而不是二阶统计量的技术，这些技术主要是得将彩色噪声呐入到了阵列处理技术的考虑范围之内。Dogan M C 等[5]率先阐释累积量是如何增加传感器阵列的有效孔径的，并在加性彩色噪声的不敏感性研究下有显著突破。Boaz Porat 等[6]提出了基于高阶累积量的MUSIC 算法。Chen Y H 等[7]开发了一种四阶算法，其性能在高斯噪声和非高斯噪声环境中比MUSIC 算法都更佳。Gonen E 等[8]利用四阶累积量进行方向定位，来研究比接收器列传感器数量还多的信号的分解。

国内有关简正波声场以及匹配场的相关研究也取得了一些成果：杨坤德[9]在基于环境扰动的匹配场和自适应匹配场领域颇有建树；王奇等[10]分析了浅海环境参数失配问题对匹配场处理的影响；邹士新等[11]进一步比较了在浅海匹配场环境中几种优化算法的性能；何怡等[12]将WKBZ 简正波理论应用于匹配场定位；李建龙等[13]对不确定海洋环境下的匹配场处理做出了相关讨论；李倩倩等[14]进一步研究了在不确定海洋环境下的贝叶斯声源定位法；肖鹏等[15]对模态滤波匹配场定位方法进行了数据验证；李风华等[16]采用水平阵进行海水声速剖面的反演研究并取得一定成果；苏林等[17]针对浅海环境下声速剖面失配引起的匹配场处理器失配问题，提出了一种自适应匹配场定位算法在声速剖面时变环境下的实现方式；陈耀明等[18]提出了多线谱加权匹配简正波处理的声源定位算法；高天赋等[19]提出了简正波分解快速迭代算法；赵闪等[20]针对基于Kraken 模型的海洋声场及相干性进行了分析；姚美娟等[21]人提出了一种基于双引导声源和warping 变换的拷贝声场计算方法。

本文介绍了一种海洋声层析环境下使用高阶累积量消除匹配场处理中高斯有色噪声的算法，基本思路为：利用水听器阵列接收到的信号数据和假设声源通过信道模型传输出的理论数据，根据一定方法计算出声源的位置[22]。选取合适的声场模型，配合先验的海洋声场环境参数，可求得水听器会接收到的模拟信号，将这个计算出来的模拟值称之为拷贝场向量。将拷贝场向量和真实接收信号进行匹配运算得到最匹配的拷贝场向量，进一步得到定位模糊表面，再结合高阶累积量，就可消除海洋声传播环境中高斯有色噪声的影响。如果真实信源位置与假设声源位置一致，则匹配场处理器有最大值输出，拷贝场向量和接收信号有最大相关，可以直接从定位模糊表面上读出信源的距离和深度，借助这两个参数便能描述信源的位置。

1 基于高阶累积量的匹配场定位技术

1.1 声场模型的选取与匹配场处理器设计简述

在声学匹配场定位探索中，最关键的部分便是声场模型的构建和计算拷贝声场的值。根据环境条件的差别，可选用不同的声场模型，相对应的求解方法也不尽相同[22]，表1 中给出了目前常见的几种声场模型的效果比较。

表1 声场模型效果一览表

通过上表的分析，本文选用简正波模型进行建模与数据处理。在选定声场模型后，最关键的是匹配场处理器的设计，采取设计思路如下：

（1）在简正波模型下，对海洋按距离和深度进行网格划分，计算每个格点接收阵列会产生的拷贝声场。

（2）将DOA 估计中的二阶MUSIC 经典算法迁移到匹配场处理中，并拓展为对接收信号求高阶累积量矩阵提高信噪比。

（3）对高阶累积量矩阵进行特征值分解，按照信源个数K取前K大的特征值对应的特征向量张成信号子空间，剩下的N-K个特征值对应的特征向量张成噪声子空间。信号子空间和噪声子空间相互正交。

（4）在子空间划分下，利用噪声子空间的特征向量和接收信号做相关运算，定位模糊表面公式为在下文中将详细给出引入高阶累积量（尤其是四阶）的情况下的定位模糊表面公式的推导过程。

1.2 匹配场处理器的定位模糊表面函数的确定

本文采用信号模型为精度较高的简正波模型，该模型在匹配场定位的应用中更适用于低频、远距离的海洋环境。通常使用距离和深度两个参数来描述分层介质中的单频点源声场。由于这种分层介质满足无水平梯度、传播具有圆柱对称性的特征，可以使用非齐次赫姆霍兹方程进行表示：

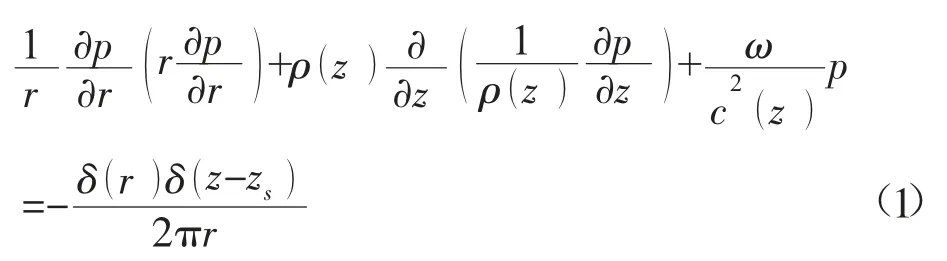
推导成符合远场环境的简正波表达式如下：

式中：kn表示第n个简正波的波数；βn表示简正波的指数衰减因子；un(z)表示正交归一的本征函数。

借助KRAKEN 简正波模型程序包进行数据处理，在程序中输入模型对应的海洋声学参数，利用有限差分求出单频点声源声场分布P(r,z)的离散解，同时利用KRAKEN 程序包处理得出的频率为ω0的单频信号在声场（r,z）处的频幅响应值，视为是该海洋环境下信源频率在ω0的信道响应h（r,z）。

之后对高阶累积量矩阵做特征分解，构造相应的噪声和信号子空间。通常选用四阶累积量来进行计算，其数学表示为：

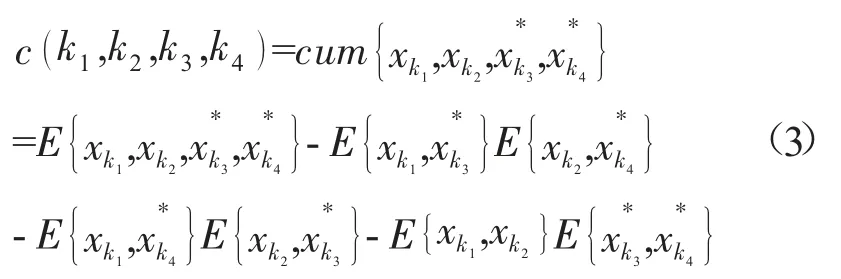
式（3）也可表示为：

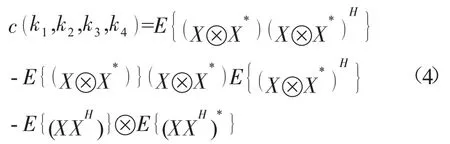
进行公式化简，得：

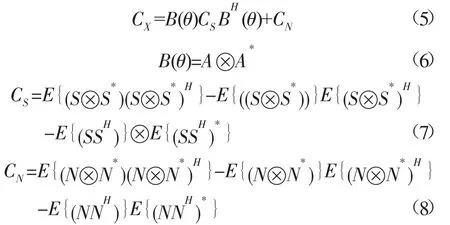
在理想高斯噪声的条件下，噪声子空间CN应为全零矩阵，但现实中噪声环境会在一定程度上偏离高斯分布，所以噪声总空间总是近似为零的小量，上式中CS就是所要求的信号子空间。

与传统的MUSIC 算法相类似，要得到匹配场处理器的定位模糊表面函数[12]，可以根据其满秩为K，H矩阵的秩也为K，HRSHH为半定矩阵，并且协方差矩阵具有K个非零特征值：μ1≥μ2≥…≥μk＞0，那么它的N个特征值为：

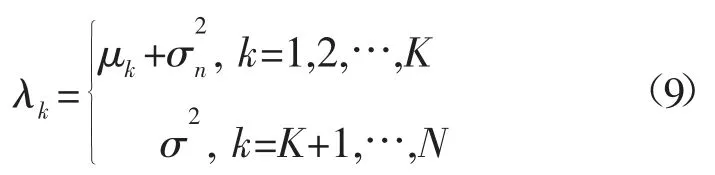
其对应的特征向量记为：e1,e2,…,ek,ek+1,…,eN，

按照特征值分解原理处理矩阵，有：

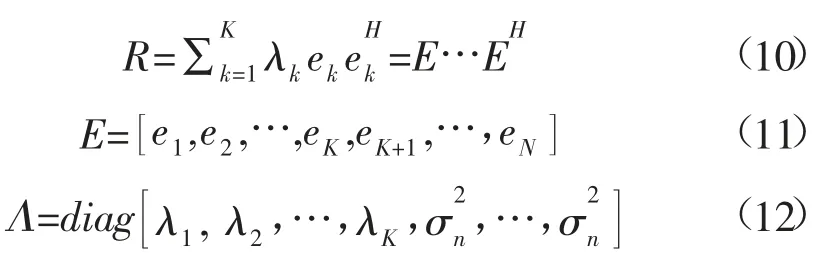
因此当i＞k时，有：

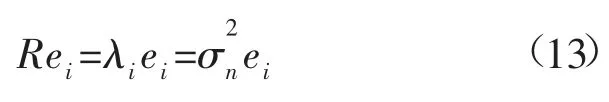
结合公式：

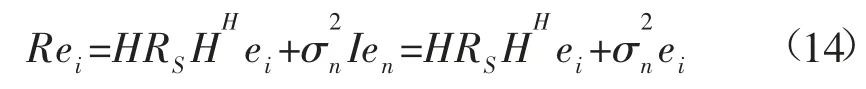
可以得到以下条件：

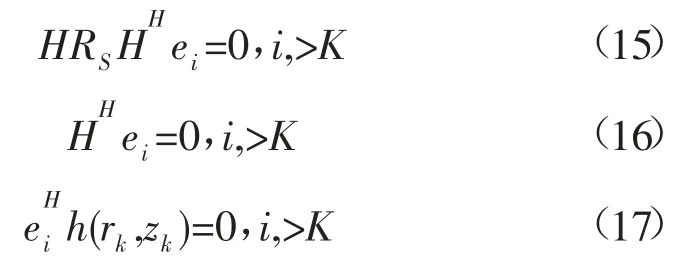
至此可以得出最小特征值对应的特征向量与拷贝声场向量正交，即K维的信号子空间与（N-K）维的噪声子空间内的向量内积为零，最终便可以得到匹配场定位函数：

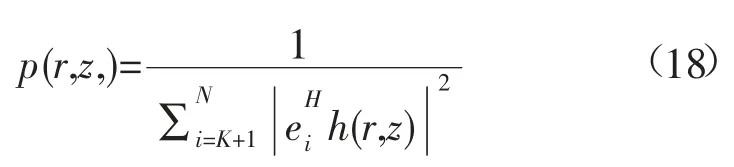
2 实验数据仿真与处理

本节利用KRAKEN 程序是在简正波传播模型的基础上，对海洋声学环境进行建模。该程序包基于Fortan 语言编写，由美国海军研究实验室和美国海军海洋系统中心共同开发，经过二十余年的改善，此程序已经成为具有全球适用性的可用来评估其它新开发的海洋声学模型的国际标准之一，因此利用此程序评估引入高阶累积量的声场算法的可靠性和可信度较高。

2.1 简正波的模态分布

进行仿真的水声场环境参数如表2 所示。

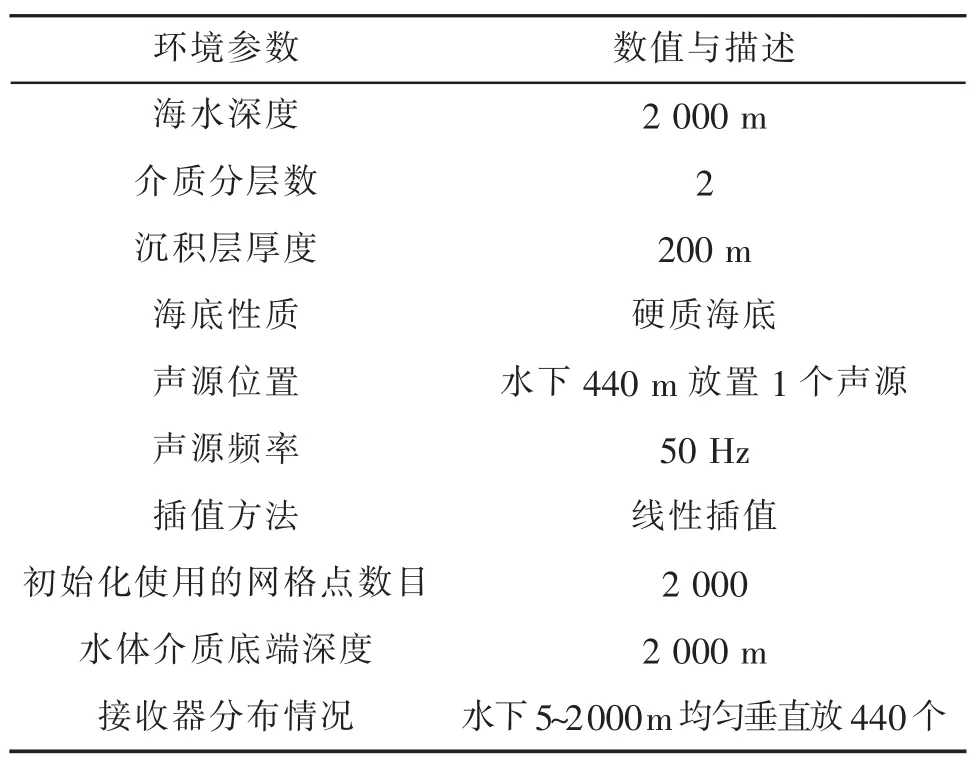
表2 简正波水声场仿真环境参数

所设置的海水中声速与密度分布情况如图1所示。

图1 模拟声场环境示意图

通过设置KRAKEN 程序中的环境文件（后缀名为.env）来生成相应的模式文件MODFIL，使用PLOTMOD 模式绘图功能，绘制出简正波在海洋中的传播与反射的情况如图2 和图3 所示。其中，图2为 1，3，5，7，9，11，13，15，17，19 阶简正波幅度随深度分布图，图3 为所有的简正波模式，共有21 阶。

图2 简正波模态分布图

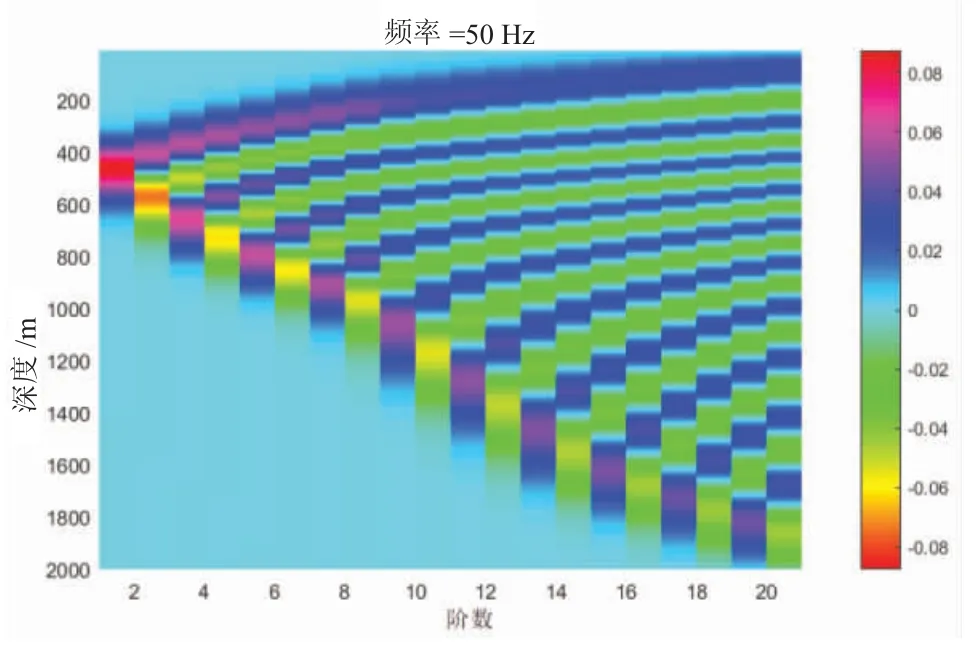
图3 简正波模态分布图

2.2 引入高阶累积量的算法与传统算法的效果比较

为了更有效地说明引入高阶累积量简正波匹配场处理器定位的效果，本文将从两个部分进行阐述，一是通过自行构建海洋环境和信号源发射器，比较传统线性匹配场处理器、自适应匹配场处理器、二阶MUSIC 算法匹配场处理器和基于高阶累积量的简正波声场匹配场处理器的定位效果，二是利用国际海洋声学数据库OALIB 提供的多种模拟测试数据进行比较。上述实验均不考虑参数失配等问题，如果在理想条件下基于高阶累积量的简正波声场匹配场处理器优于其它3 种，对其进行的深入讨论才有价值，因此本部分比较的是在完全匹配的理想条件下引入高阶累积量的方法与其他3 种方法的定位效果。

将上文中提到的四种匹配场处理器在-30～15 dB 的每个信噪比下进行一百组定位实验并观察其定位匹配成功率。假设在海平面下的5～100 m 的地方深度每间隔5 m 均匀放置水听器，之后按照不同的信噪比在信号中掺入白噪声或者自定义的彩色噪声（主要指的是红噪声），利用上述4 种常见的处理器从-30～15 dB 的每一个信噪比下进行100 次信号处理实验并观察匹配定位成功率。进行上述实验模拟的海洋声场环境参数如表3 所示。

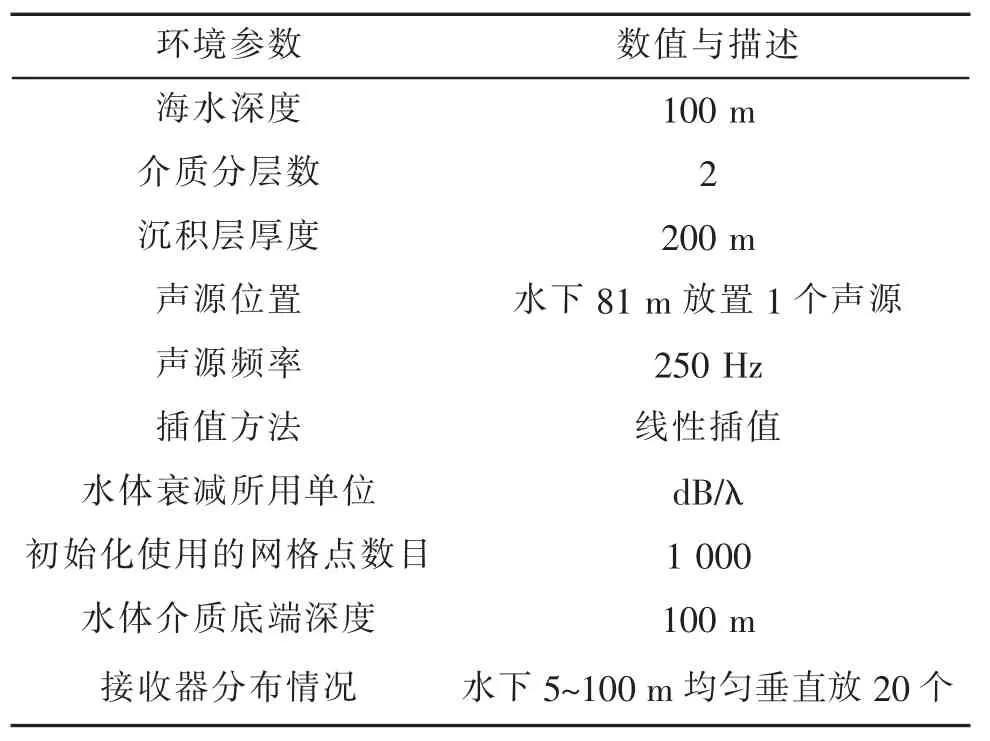
表3 实验仿真的水声环境参数

接收器分布情况为水下5～100 m 均匀垂直放20 个实验所采用的声场模型的声速以及介质密度等信息的情况如图4 所示。

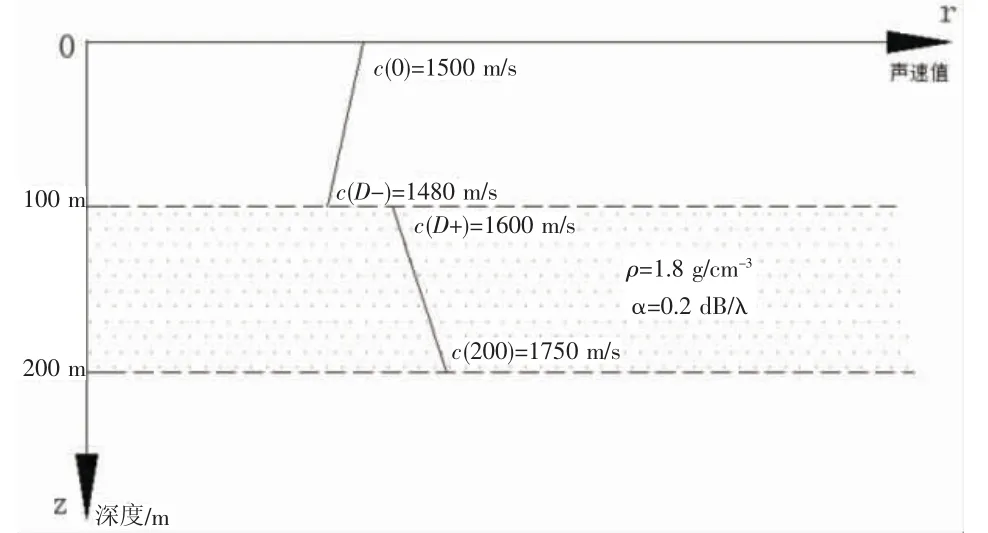
图4 实验模拟声场环境示意图

上述仿真实验的结果如图5 和图6 所示。

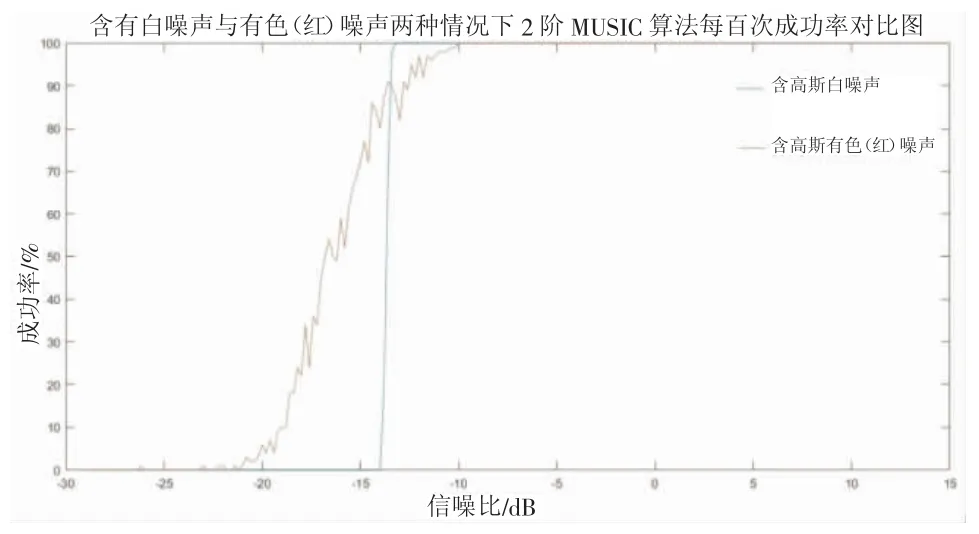
图5 含有高斯白噪声与有色（红）噪声两种情况下的2 阶MUSIC 算法定位成功率统计图

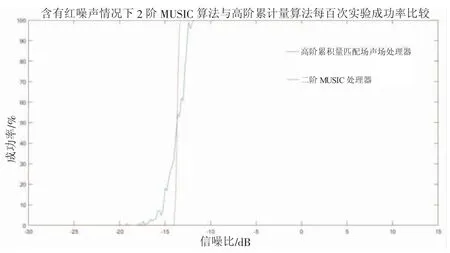
图6 含有色（红）噪声情况下2 阶MUSIC 算法与高阶累积量算法定位成功率比较

实验显示：

（1）在图5 中，在含有有色（红）噪声两种情况下，二阶MUSIC 算法的定位效果相比较含有白噪声的情况下会受到明显影响。

（2）在图6 中，在引入有色（红）噪声的情况下，高阶累积量算法能一定程度上弥补二阶MUSIC 算法的缺陷，提高匹配场定位的成功率。

随后，选择其中一个比较有代表性的信噪比数值进行实验分析，在信噪比为-15 dB 的情况下，四种处理器的定位效果对比如图7 和图8 所示。

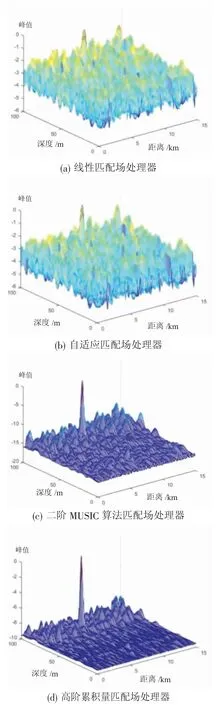
图7 COLNOISE 海洋环境下掺杂白噪声情况下信噪比为-15dB 的匹配场定位模糊表面示意图

图8 COLNOISE 海洋环境下掺杂有色（红）噪声情况下信噪比为-15dB 的匹配场定位模糊表面示意图

实验显示：

（1）当信噪比为-15 dB，在含有白噪声的环境下，对比上述四种算法输出的定位模糊表面三维效果图，可发现高阶累积算法能够更有效的抑制旁瓣，甚至相比于二阶MUSIC 算法的旁瓣更少，定位效果更优。

（2）当信噪比为-15 dB，在含有有色噪声（红噪声）的情况下，对比上述四种算法输出的定位模糊表面三维效果图，可发现基于高阶累积量的简正波声场匹配场处理器仍能有效抑制旁瓣，且在这种情况下二阶MUSIC 算法匹配场处理器输出的定位模糊表面上存在多个峰值点，定位失败，但基于高阶累积量的简正波声场匹配场处理器仍能实现成功定位。

2.3 国际海洋声学数据库（OALIB）数据测试

匹配场处理解决了在海洋波导环境中寻找声源的声学逆问题（也被应用在求解海洋环境参数的问题中），除了最常用的线性处理器和自适应处理器以外，为了鉴别新提出的各种处理器的性能和对环境参数失配的敏感程度，1993 年，Porter M B[23]在文章中提及了一套测试数据并总结了实验中遇到的相关问题，这便是之后国际上通用的海洋声学数据库（OALIB），其用来对匹配场处理器进行效果的评测。因此，为了进一步验证基于高阶累积量的匹配场处理算法在海洋声层析环境下实际应用中的定位效果，本文中主要考虑了海洋环境中存在的高斯白噪声和有色噪声，为了检验算法的抗干扰能力，我们使用了国际海洋声学数据库（OALIB）中的多种模拟测试数据进行测试。

测试所采用的数据为两类，包括标准情况（CALIB）测试数据和含有有色噪声（COLNOISE）测试数据，每类数据取信噪比为40 dB，10 dB 和-5 dB 3 种条件下进行测试，测试的四种匹配场处理器与上文中提到的四种处理器保持一致。设定的测试条件为：垂直接收阵列覆盖纵面上所有海水层，共含有20 个水听器阵元，阵元之间间隔5 m，水下5 m的阵元为最靠近海平面的，声源频率设定为250 Hz。并且只有在标准情况（OALIB）背景的情况下，声源的位置是已知的，深度为50 m，距离为7.5 km。有色噪声（COLNOISE）的情况下，声源位置是未知的。

2.3.1 标准数据（CALIB）测试情况 测试数据采用的声场环境是最为典型的Pekeris 声场模型，同时添加了上文中提到的三类不同信噪比的白噪声。具体环境条件如下：声源频率250 Hz，声速C1=1 500 m/s，深度D=100 m，海洋底部声速C2=1 590 m/s，衰减系数α=0.5 dB/λ，密度ρ=1.2 g/cm3。源距离垂直阵列7.5 km，距离水平面深度50 m。CALIB 所采用的声场模型示意图如图9 所示。

图9 CALIB 采用的Pekeris 声场模型

该流程主要思路是通过上一次处理的前向模型来调整未知参数直至模型提供的数据与采集到的数据成功匹配，在最优匹配的情况下便可认为发现未知参数。上述过程中的TL 曲线如图10 所示。

图10 CALIB 环境下TL 曲线

从模型化声压场中可确定水听器坐标，然后将这些量仅和测量的数据进行比较，比较公式如下：

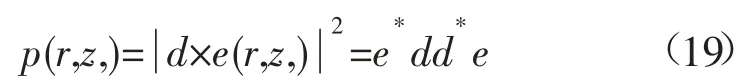
上式中，e(r,z)表示范围r和深度z的归一化预测，（）* 表示求矩阵的共轭转置。为了发现声源点的位置，我们可以寻找功率峰值，而所述的功率图便可以表示定位模糊表面。

三组CALIB 标准数据的实验情况如图11～图13 所示。

2.3.2 含有有色噪声数据（COLNOISE）测试情况 在生成的有色噪声测试数据（COLNOISE）的声场环境中，海洋为分层均匀的环境，在沉积层的上层，声音在该层面传播速度从1 600 m/s 均匀线性增加到1 750 m/s，下层的传播速度恒定，值为1 750 m/s，而在上下层中间是负梯度的声速剖面，具体示意图如图14 所示。

在三组COLNOISE 数据的实验情况如图15～图17 所示。

实验显示：无论在CALIB 还是COLNOISE 的环境下，基于高阶累积量的简正波声场匹配场处理器相比于其他三种处理器，能够更有效的定位峰值，且能有效抑制旁瓣。

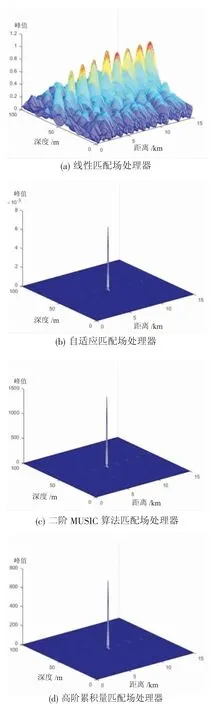
图11 CALIB 第一组数据（信噪比为40 dB）采集情况下三维定位模糊表面

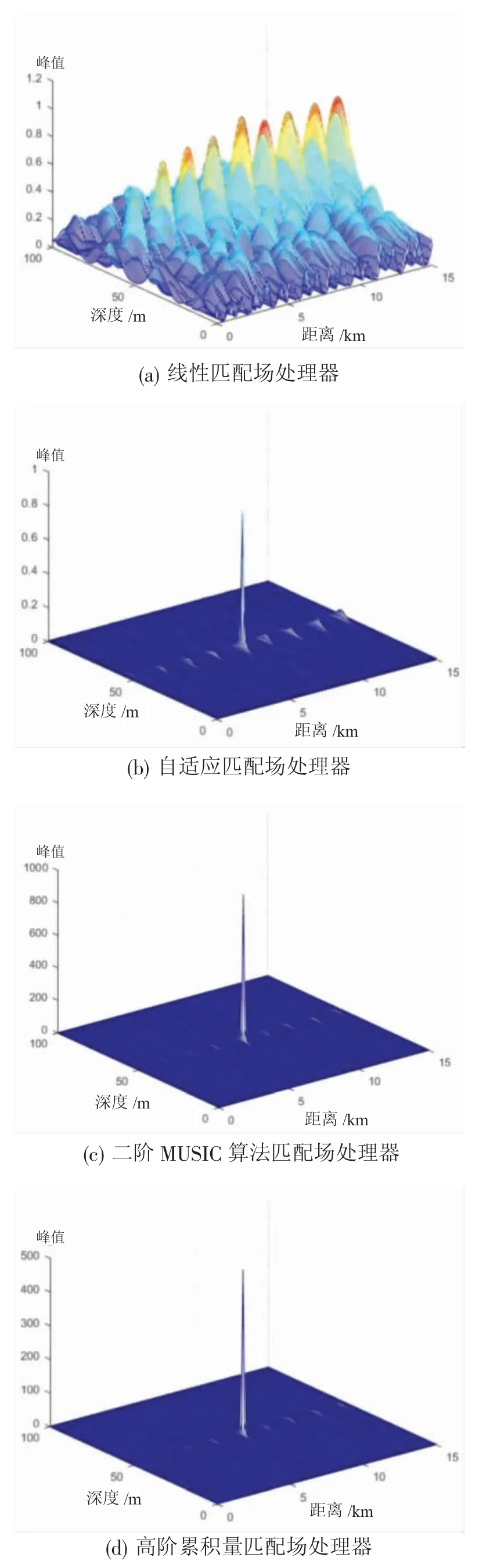
图12 CALIB 第二组数据（信噪比为10 dB）采集情况下三维定位模糊表面

图13 CALIB 第三组数据（信噪比为-5 dB）采集情况下的三维定位模糊表面

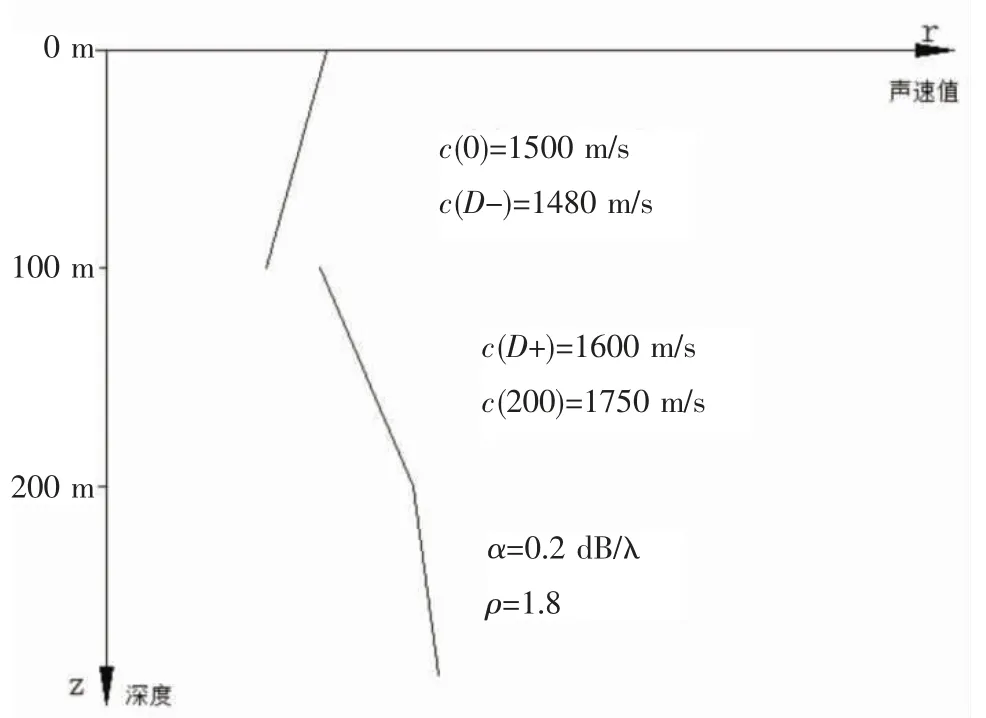
图14 COLNOISE 声场环境

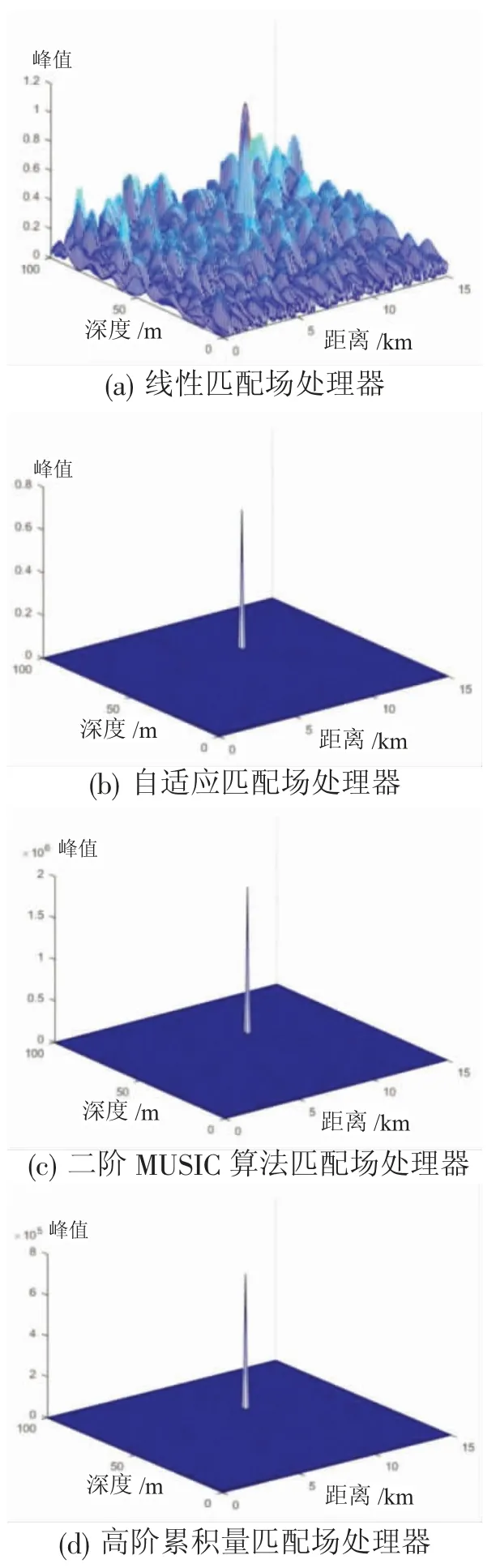
图15 COLNOISE 第一组数据（信噪比为40 dB）采集情况下的三维定位模糊表面

图16 COLNOISE 第二组数据（信噪比为10 dB）采集情况下的三维定位模糊表面

图17 COLNOISE 第三组数据（信噪比为-5dB）采集情况下的三维定位模糊表面

3 实验结论

（1）在从-30～15 dB 的每个信噪比下进行一百组定位实验并观察其定位匹配的成功率的实验中，研究发现：在含有有色（红）噪声两种情况下，二阶MUSIC 算法的定位效果相比较与含有白噪声的情况下会受到明显影响（图5），这主要是因为二阶MUSIC 算法的适用范围有限，因此不能很好地分离有色噪声和白噪声。在引入有色（红）噪声的情况（图6）下，高阶累积量算法能够造一定程度上弥补二阶MUSIC 算法的缺陷，提高匹配场定位成功率。

（2）当信噪比为-15 dB 并且含有白噪声的环境下，通过上述四种算法输出的定位模糊表面三维效果图可以看出，高阶累积算法能够更有效的抑制旁瓣（图7），甚至相比于二阶MUSIC 算法的旁瓣更少，定位效果更优。当信噪比为-15 dB 并且含有有色噪声（红噪声）的情况下，对比上述四种算法输出的定位模糊表面三维效果图，依然可以看出高阶累积量能更有效的抑制旁瓣（图8），值得一提的是在这种情况下二阶MUSIC 算法匹配场处理器输出的定位模糊表面上存在多个峰值点，定位失败，但高阶累积量匹配场处理器则实现了成功定位，这体现出引入高阶累积量的优势所在。

（3）在海洋声学数据库（OALIB）的测试下可以看出，在CALIB 和COLNOISE 环境下，基于高阶累积量的匹配场处理器有着显著高于其他三种处理器的定位精确度（图11～图13，图15～图17），并且有旁瓣低和峰值定位准确的优点，在COLNOISE 第三组数据集下，即有色噪声环境下，可以清楚的看见二阶MUSIC 算法的旁瓣较高，而高阶累积量算法输出的定位模糊表面基本没有旁瓣，这进一步体现了基于高阶累积量的匹配场处理器在有色噪声环境下的优异性能。

鉴于上述实验均是在理想的匹配环境下进行，可证明这种基于高阶累积量的匹配场处理器能够在一定程度上实现对于有色噪声的抑制，提高信噪比，为下一步讨论在更为复杂海洋环境下对该匹配场处理器的方法性能验证奠定了基础。

4 总结与展望

通过实验研究分析，发现基于高阶累积量的匹配场处理器相比于其它处理器具有以下优势：（1）对契合高斯分布的噪声求高阶累积量，其值恒为零，而非高斯噪声求高阶累积量，其结果并不是恒为零，对高斯噪声不敏感。因此使用高阶累积量为解决一般非高斯信号噪声中有色噪声的处理提供了一种借鉴思路；（2）高阶累积量能描绘信号更详细的信息，比如描述信号的相位，因此可以用来解决信号或子波的重构问题；（3）高阶累积量本质上是一种高斯偏离度的度量，可以用于检测系统非线性。

但是，这种基于简正波匹配场的处理技术同时也存在着一些缺点：（1）当高频深水时其计算量大，且不适用非水平分层介质，一旦海洋环境不够理想，对整个基于此模型的处理器效果影响较大；（2）在海洋声学数据库中尚未对处理器进行参数失配的敏感性验证；（3）利用高阶累积量的简正波声场匹配场处理器和基于二阶MUSIC 算法的相比，存在计算量过高的问题，甚至远大于协方差矩阵的计算量，这是后续需要完善的部分。