浅谈数列的极限及其应用

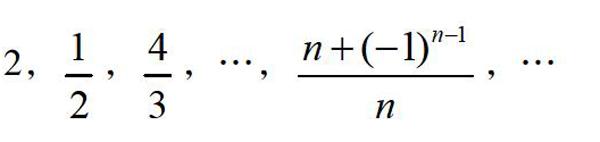
摘  要：本节探讨如何用数学的语言精确地刻画数列无限变化的过程。强调极限是在求解精确解的问题中产生，以及利用极限解决问题的思想与方法。

关键词：数列  函数  极限

高等数学是为大学一年级新生开设的一门数学基础课。而数学课程具有的较强理论性使得学生常常对其形成一种枯燥乏味的感受。如何结合实际背景，在传统的数学课中注入丰富的数学思想与文化是高等数学教与学中一个值得探讨的问题^[1]。

在同济大学第7版的高等数学中，第一章第2节展开了对数列极限的分析^[2]。在前面的课程中我们介绍了函数的概念，这是定义在数集与数集之间的映射。而当输入的数集为自然数集时即为一种特殊的函数：数列。由于数列的这一特殊性，其常常用来描述某些无限变化的过程问题，例如割圆术等。通过无限变化的过程来求解一些问题的精确解。这也是中国古代早期的朴素的極限思想的体现。古今中外的数学家都尝试着描述这个无穷无尽的抽象的变化过程。那怎样给出严格的数学形式的极限定义呢？这就是本节探讨的主题。

一、极限思想的发展

首先，结合引例的分析引导学生感受极限思想的发展。例如《庄子·天下篇》中的“一尺之棰，日取其半，万世不竭”。三国时代数学家刘徽使用割圆术，分割圆为192边形，得：3.141024<π<3.142704。瑞典数学家科赫提出的“不断生长”的科赫雪花。

但是如何给出严格的数学定义来刻画数列的变化趋势却是一个长久未能解决的问题^[3]。这使微积分的发展产生了严重的危机。

二、数列极限的定义

刻画数列在无限变化过程中的趋势是一个比较抽象的过程。接下来，采用逐层深入的方式讨论极限定义的提出过程。结合例题归纳出需要引入的变量。

例如：

三、数列极限的应用

最后，运用数列极限的定义判断数列的敛散性，分析数列在无限变化过程中的精确解。并且，将数列的变化趋势与实际问题的分析相结合^[4]。列举不同类型的函数极限问题。首先讨论学生比较熟悉的等比数列。探讨其在无限变化过程中的变化趋势，强调数列中的参数对数列敛散性的影响。接下来运用这一结论解释与分析实际问题，加深大家对数列极限的理解。在极限的分析中注意启发同学们提出问题，根据学生的想法及时调整讲授内容的侧重点。其次，在极限的证明过程中以板书的形式与学生一起揣摩如何进行不等式的放缩。注意对常用技巧的理解与积累。运用对比的方式让学生感受不同程度的放缩产生的差异性。

本节探讨了数列极限的定义。采用了问题引导式的教学方法，结合极限思想的发展过程感受极限定义的严谨性与必要性。思考函数在无限变化过程的刻画与分析方法。如何将其思想推广到一般的函数情形，这是下一次课的内容。

参考文献

[1]左玲.浅谈人工智能时代的工科数学教育[J].考试周刊，2018.

[2]同济大学数学系.高等数学（第七版上册）[M].高等教育出版社，2018.

作者简介

左玲（1981.8—），女，汉族，籍贯：湖北武汉，博士研究生，副教授，工作年限15年，湖北工业大学，理学院。