军校“信号与系统”课堂教学设计研究
贺寅 徐池 韩东 李利 王永超


摘 要:信号的运算和分解是“信号与系统”课程中的一个重要知识点。在课堂教学中,结合章节的内容要点,设计多个算例,采用MATLAB软件进行编程仿真,将抽象的理论知识与直观的图形演示相结合。由于解题思路和编程逻辑并不唯一,促使学员主动寻找一题多解、举一反三的答案,开阔了学习思路、激发了创新热情,为“信号与系统”课程教学方式改革实践提供了有益参考。
关键词:信号与系统;信号运算和分解;仿真教学
中图分类号:G642.3 文献标识码:A 文章编号:2096-4706(2020)09-0071-05
Research on Classroom Teaching Design of “Signal and System”in Military Academy
——Taking Simulation Teaching of Signal Operation and Decomposition as an Example
HE Yin,XU Chi,HAN Dong,LI Li,WANG Yongchao
(PLA Dalian Naval Academy,Dalian 116018,China)
Abstract:The operation and decomposition of signals are an important knowledge point in the course of “Signal and System”. In classroom teaching,combining the main points of the chapter,designing multiple calculation examples,using MATLAB software for programming simulation,combining abstract theoretical knowledge with intuitive graphical presentation. Because the problem-solving ideas and programming logic are not unique,students are motivated to actively find answers to multiple questions and inferences,which broadens their learning ideas and stimulates enthusiasm for innovation. It provides a useful reference for the reform and practice of the “Signal and System” teaching method.
Keywords:signal and system;signal operation and decomposition;simulation teaching
0 引 言
“信号与系统”课程学习的一个核心问题是对各种类型的信号进行一种或者一系列处理。目前,在绝大多数教材中,信号运算知识的介绍主要包括信号的移位、信号的反褶、信号的尺度倍乘、信号的微分、信号的积分以及信号的相加或者相乘[1];另一个常用的信号运算就是信号的分解,这是进行系统响应分析的基础。采用传统的“理论讲解+公式推导”的方式进行教学,学员感到直观性不强,理解比较困难、过程太抽象,难以深刻记忆。因此,在这部分知识点的课堂教学设计中,可以借助MATLAB软件,将这些抽象的理论知识,通过直观、动态的图形以及动画仿真直观地展现给学员,帮助他们理解信号运算和分解的相关概念和理论知识[2]。
1 信号运算
1.1 信号的移位
信号的移位(时移或延时)是指,让信号f(t)沿着时间轴t整体左移或者右移,信号f(t)是一个三角波信号,通过MATLAB仿真观察信号的移位结果,如图1所示。
从图1中可以觀察到,对于信号f(t),f(t+2)是把信号沿着时间轴t向左平移2个单位,f(t-2)是把信号沿着时间轴t向右平移2个单位。
信号的移位在实际工作中比较典型的一个应用就是雷达系统发现目标的原理,雷达首先利用发射机天线向外辐射一个电磁信号,这个信号在传播的过程中,碰到目标物体,形成一个电磁回波信号返回,这个回波信号将被雷达的接收机准确接收。经过分析,回波信号与发射信号之间在时间上产生了一定的延迟t0,利用这个延迟的时间t0,结合电磁波在空间中的传播速度,就可以通过数学计算得到雷达所在位置与目标物体位置之间的距离。
2.2 信号的反褶
信号的反褶是指,让信号f(t)沿着t=0进行反褶,信号f(t)是一个正弦波信号,通过MATLAB仿真观察信号的反褶结果,如图2所示。
从图2中可以观察到,信号反褶后的结果没有改变信号的大小和形状,f(-t)就像是f(t)沿着t=0对称的镜像。
2.3 信号的尺度倍乘
信号的尺度倍乘(压缩与扩展)是指,对信号f(t)进行压缩和扩展,信号f(t)是一个三角波信号,通过MATLAB仿真观察信号的尺度倍乘结果,如图3所示。
从图3中可以观察到,当变量t的系数大于1时,是对原波形进行压缩,如图3(c)中的波形;当变量t的系数小于1时,是对原波形进行扩展,如图3(a)中的波形。
需要注意的是,信号经过尺度倍乘变换后,其波形完成压缩或者扩展,而波形端点并不是被任意画在时间轴上的,端点的数值变化需要通过数学计算得到准确的结果,通过具体的例题进行说明:
信号f(t)是一个三角波信号,如图4(a)所示,信号f(t)波形的两个端点分别是t01=-2,t02=2,f(t01)=f(t02)=0,求f(2t)和f(1/2t)的波形。
对于f(2t),根据尺度倍乘的变换规则,三角波信号是要压缩的。尺度倍乘后,并不改变f(t)的函数值,计算波形的两个端点:
f(t01)=f(2*t11)
f(t02)=f(2*t12)
t11=1/2*(t01)=1/2*(-2)=-1
t12=1/2*(t02)=1/2*(2)=1
变换后的波形如图4(b)所示。
对于f(1/2t),根据尺度倍乘的变换规则,三角波信号是要扩展的。尺度倍乘后,并不改变f(t)的函数值,计算波形的两个端点:
f(t01)=f(1/2*t21)
f(t02)=f(1/2*t22)
t21=(t01)/(1/2)=(-2)/(1/2)=-4
t22=(t02)/(1/2)=2/(1/2)=4
变换后的波形如图4(c)所示。
信号的尺度倍乘在实际工作中比较典型的一个应用就是播放磁带中的录音,假如将f(t)看成是按照正常的速度播放磁带中的录音;那么,对于f(2t),就是按照双倍的速度播放磁带中的录音;相反,对于f(1/2t),就是按照正常情况下一半的速度播放磁带中的录音。
2.4 信号的微分和积分
在数学中已经介绍过,信号的微分和积分是一对逆运算,通过MATLAB仿真观察信号的微分和积分结果,如图5、图6所示。
从图5、图6可以观察到,信号微分后,将会突出显示信号变化的部分,而信号积分后,效果与微分正好相反,变化的部分逐渐平滑。
信号的微分和积分在实际工作中比较典型的一个应用就是进行数字图像信号的处理,比如图像信号经过微分以后,边缘轮廓会变得更加清晰;同样的图像信号经过积分以后,边缘轮廓会变得模糊不清。
2.5 信号的相加和相乘
信号相加,其实就是对每个时点的幅度逐一进行数学相加(同方向的相加、不同方向的相减);信号相乘,实际是信号的函数相乘,构成一个新的信号,通过MATLAB仿真观察信号的相加和相乘结果,如图7、8所示。
信号的相乘在实际工作中比较典型的一个应用就是通信系统中的线性调制,比如在绝大多数通信中均得到广泛运用的AM调制技术、DSB调制技术、SSB调制技术、VSB调制技术4种,它们都是幅度调制技术,其原理是:将一个基带的承载着有用消息的信号,与一个频率较高的载波相乘,经过这种信号运算,实现了将基带信号的频谱搬移到更高的频段。这种经过调制处理的信号有多种优点,可以使用尺寸较短的天线将信号发射出去;同时,通过这种相乘的调整,还可以让信号主动适应不同类型传输信道的要求。
2.6 信号的综合运算
在实际中,通常碰到的情况是对一个信号进行多种运算处理,信号运算教学中的重点,就是信号的移位、反褶、尺度倍乘三者的综合计算,通过具体的例题进行说明:
信号f(t)是一个三角波信号,求解f(2-2t)。
(1)按照“尺度倍乘→反褶→移位”的顺序进行仿真运算:1)先把信号f(t)进行压缩处理;2)将压缩处理后的信号f(2t)沿着t=0进行反褶;3)将f(-2t)沿着时间轴平移,需要注意“向左还是向右平移”“平移多少个单位”,通过设置问答,进行教学互动,找出答案。仿真运算的过程,如图9所示。
(2)按照“反褶→移位→尺度倍乘”的顺序进行仿真运算:1)先把信号f(t)沿着纵轴进行反褶;2)将反褶后的信号f(-t)沿着时间轴平移,需要注意“向左还是向右平移”“平移多少个单位”,通过设置问答,进行教学互
动,找出答案;3)对信号f(1-t)进行压缩处理。仿真运算的过程,如图10所示。
从图9、图10可以观察到,虽然信号运算的顺序不同,但最终运算结果是一致的。当然,还可以采用其他的运算顺序进行仿真,留给学员作为一次课外练习,自己动手编程仿真。同时需要注意一点:信号所有的运算、变换都是针对变量t来进行的[3]。
3 信号分解
在信号与系统的分析中,经常会把信号分解成一些简单的、基本的信号,达到将复杂的问题进行简化的目标,而且还可以使问题的分析过程变得更加清楚[4]。这里结合MATLAB仿真,以信号的奇偶分解、正交分解和脉冲分解为例做重点讲解。
3.1 信号的奇偶分解
信号可以分解为一个偶分量f1(t)和一个奇分量f2(t),并且偶分量f1(t)=0.5*[f(t)+f(-t)],奇分量f2(t)= 0.5*[f(t)-f(-t)],信号f(t)为一个正弦波信号,通过MATLAB仿真观察分解的结果,如图11所示。
3.2 信号的正交分解
一个矩形脉冲信号可以分解为各次谐波的正弦信号与余弦信号叠加,通过MATLAB仿真观察信号的正交分解结果,如图12所示。
从图12中观察可以看到,随着正交分解的项数从10项到100项逐渐增大,分解的各次谐波项叠加起来以后,越来越逼近于原方波信号。信号的正交分解知识点非常重要,它是学习连续时间系统频域分析的重要基础,常说的傅里叶级数就是以信号的正交分解为核心内容的。
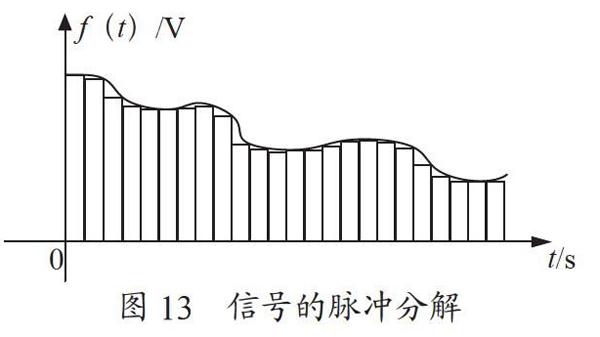
3.3 信号的脉冲分解
一个信号可以分解为N个矩形窄脉冲分量之和,如图13所示。从图13中可以看出,随着矩形窄脉冲分量的个数N逐渐增多,分解后的结果将会越接近于原信号;当脉冲分量的个数趋向于+∞时,可以近似认为等同于原信号[5]。
4 结 论
本文针对“信号与系统”课程教学中“信号的运算和分解”知识点,结合MATLAB编程,详细分析和讲解了信号运算和分解的求解方法。设计的仿真用例,一方面可以作为课堂教学中的多媒体演示素材,直接加以运用;另一方面也可以将这些仿真用例交给学员,作为课外练习使用,强化学员主动思考、分析和解决问题的能力。同时,对比传统教学方式,仿真教学方法的应用,极大地提升了学员对课程的兴趣度,课堂气氛更加活跃,达到良好效果。
參考文献:
[1] 郑君里,应启珩,杨为理.信号与系统:第3版 [M].北京:高等教育出版社,2011.
[2] 王宏伟,张文凯,齐臣杰,等.MATLAB在信号分解与合成实验教学中的应用 [J].科技创新导报,2013(22):165-166.
[3] 谢自梅,段新涛,岳冬利.《信号与系统》中信号运算的教学探讨 [J].教育教学论坛,2015(31):193-194.
[4] 陈后金,胡健,薛健.信号与系统 [M].北京:高等教育出版社,2007.
[5] 吴大正.信号与线性系统分析:第4版 [M].北京:高等教育出版社,2005.
作者简介:贺寅(1986.08—),男,汉族,甘肃庄浪人,助教,硕士,研究方向:军事通信。

