具非正中立项的二阶非自治延迟动态系统的动力学性质研究

李继猛，杨甲山

（1.邵阳学院理学院， 湖南 邵阳422004； 2.梧州学院大数据与软件工程学院， 广西梧州543002）

0 引 言

微分系统的定性理论在物理学、生物种群动力学、机械控制、神经网络及生物制药等领域都具有广泛的应用背景。由于科学技术的迅猛发展，进入20世纪90 年代， 微分系统的一个新分支——时间测度链上的动态系统诞生了。其一出现就引起了国内外广大学者的高度关注， 研究成果也非常丰富， 发表了大量有关时间测度链上动态系统理论的研究论文和专著[1-15]。基于这些实际应用背景， 本文研究了时间测度链T 上具非正中立项的二阶非线性非自治延迟动态系统:

的动力学性质，其中，z(t)=x(t)-p(t)x(τ(t))。系统(1)的解及其动力学性质(振动性)的定义可参见文献[1-11]。假设:

(H1) T 为任意时间测度链，且 sup T= ∞;α＞ 0是实常数;Δ 表示时间测度链T 上的Δ-导数记号，详细叙述可参考文献[1]。

(H2) 函 数r，p，q∈Crd(T，R)， 且r(t)＞ 0， 0 ≤p(t)≤p0＜1(p0是常数)，q(t)＞ 0。

(H3)τ∈Crd(T，T)是延迟函数，且。

(H4)δ∈Crd(T，T)是Δ-可微的延迟函数， 且0＜δ(t)≤t，δΔ(t)＞ 0，limt→∞δ(t)= ∞。

(H5) 函数f∈C(R，R)，且当u≠0时，(常数k＞0)。

考虑系统(1)是正则的情形， 即系统(1)满足条件

最近，中外学者发表了许多有关时间测度链上动态系统理论(特别是振动理论等)的研究成果[1-15]，但在各类一阶及二阶动态系统讨论中，其中立项系数都是非负的[2-6]，对中立项为非正函数的研究成果很少。作为特殊情形，当T=R 时，文献[7-9]研究了一类具非正中立项的二阶微分方程:

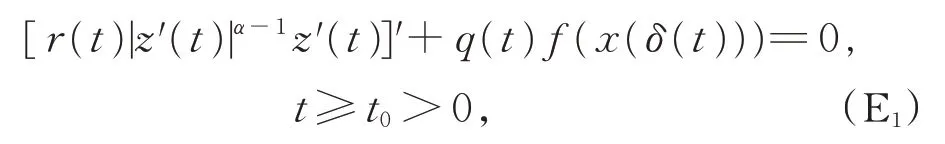
其中z(t)=x(t)-p(t)x(τ(t))， 在 条 件下得到了上述方程振动的若干充分条件。其主要结果如下:

定理 A[7]设r(t)＞ 0，-p≤p(t)≤ 0(常数 0＜p＜1)， 当x≠0时，f(t，x)sgnx≥q(t)|x|α， 并且方程(E1)满足进一步，如果有函数ρ(t)∈C1([t0，∞ )，(0，∞ ))，使得

此为文献[7]中的定理3.1， 此判别准则简单便捷，但不够细腻。之后，文献[8]改进了此定理，结果如下:

定理 B[8]设r(t)＞ 0，r'(t)≥ 0，-p≤p(t)≤0(常数0＜p＜1)， 当x≠0时，f(t，x)sgnx≥q(t)|x|α， 并且方程 (E1)满足且进一步，如果有函数ρ(t)∈C1([t0，∞ )，(0，∞ ))，使得

则方程(E1)的每个解x(t)或者振动或者。

此为文献[8]中的定理3.1， 也是文献[9]中的定理 2。只可惜定理 B 中增加了条件“r'(t)≥ 0”， 使用时会受到一些约束。

当T 为任意时间测度链时， 文献[10]研究了一类具非正中立项的二阶动态系统:

的振动性，得到了上述系统振动的一些充分条件，结论如下:

定理 C[10]设条件(H1)～(H4)及(C)成立，α≥1是2个正奇数之商，δ([t0，∞ )T)=[δ(t0)，∞ )T， 如果

定理C要求“α≥1是2个正奇数之商 ，δ([t0，∞ )T)=[δ(t0)，∞ )T”， 而且条件(C3)验证较麻烦， 当α为任意正实数时得不到系统的振动结果。

以上说明，现有文献中的关于动态系统振动理论的研究成果是不完善的。本文利用Riccati(黎卡提)变换技术及各种分析技巧研究系统(1)， 获得了系统(1)的 2 个新的动力学性质(振动准则)， 改进并丰富了动态系统的振动理论。

1 引 理

引理 1设条件(H1)～(H5)及(C)成立，x(t)是系统(1)的最终正解， 则函数z(t)最终必是下列2 种情形之一:

证明由引理条件知， 存在t1∈[t0，∞ )T，使得x(t)＞ 0，x(τ(t))＞ 0，x(δ(t))＞ 0，t∈[t1，∞ )T。由系统(1)，当t∈[t1，∞ )T时， 有

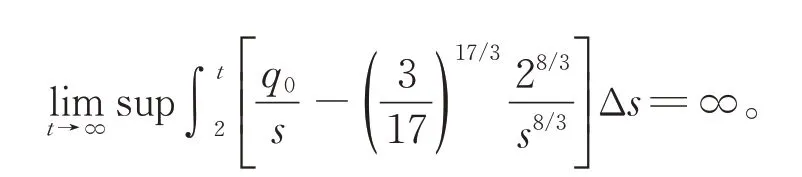
由定理2 知，系统(16)的每个解x(t)或者振动或者。

注 1 由例1 和例2 可知，验证本文所得到的充分条件非常便捷。此外，由于方程(15)和(16)的中立项系数是负的，因此，文献[1-12]中的定理都不适合方程(15)和(16)。

由于本文定理要求 0 ≤p(t)≤p0＜1， 且函数z(t)的符号是无法确定的， 因此，得到的结论只能是“系统的每个解x(t)或者振动或者渐近于0”，此结果在一定程度上具有不确定性。 能否将条件0 ≤p(t)≤p0＜1放宽为0≤p(t)≤p0＜∞、能 否 寻 找到新的条件确保系统(1)的每个解都振动，是值得进一步研究的课题。