关于伯努利多项式和Dirichlet L-函数的均值问题

张艺雪

（西北大学数学学院， 陕西西安710127）

0 引 言

q＞ 1 是一个整数，s=σ+it是一个复数，χ表示任意模q的Dirichlet 特征。著名的DirichletL-函数L(s，χ)由级数形式定义:

事实上，对于模q的主特征χ0，L(s，χ0)除了s=1 时留数为的简单极点之外都是处处解析的，其中φ(q)为欧拉函数。如果χ≠χ0，那么L(s，χ)是一个关于s的整函数。

L(s，χ)函数在解析数论中具有重要地位，许多问题都与其密切相关。例如，哥德巴赫猜想、素数的分布、Dirichlet 除数问题以及其他著名的数论问题。所以，该领域的任何实质性研究进展都将促进数论的进一步发展。正因如此，学者们展开了对L(s，χ)性质的研究，并获得了一系列有趣的结果[1-11]。例如， WALUM[1]证明了等式：

ZHANG[2-3]研究发现，对于任意奇数q≥ 3，有等式

同时， DirichletL-函数与广义伯努利多项式Bn，χ密切相关。事实上，对任意q＞ 1 的整数，χ是模q的 Dirichlet 特征，可得[12-15]

若取x=0，那么Bn(0) =Bn为伯努利数。它们与Riemann zeta-函数ζ(s)密切相关。

最近，BAYAD 等[14]研究了L-函数与伯努利多项式乘积的均方值，并证明了一系列有趣的等式。

受文献[14]启发，本文将考虑涉及伯努利多项式的卷积和的计算问题：

关于此类型和的研究有很多，如斐波那契数列、加泰罗尼亚数、勒让德多项式、切比雪夫多项式、Fubini 多项式、欧拉数和欧拉多项式等[16-24]，但尚未见到有关伯努利多项式的研究结果。

本文用初等方法研究式(4)的计算问题，并在k=3 时给出一个新的有趣的恒等式。在应用方面，给出一系列包含伯努利数的等式。经推广，获得了2 个与DirichletL-函数相关的简单结果。

方便起见，首先介绍经典高斯和的定义。

假设q和m是整数，且q＞ 1。对于任意模q的特征χ，定义[1]

其中，e(y) =ey，如果χ是模q的原特征或(m，q)=1，那么有

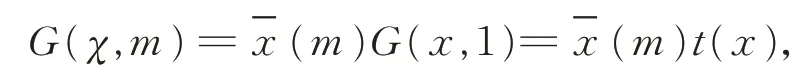
称G(χ，1) =τ(χ)为经典高斯和。

关于经典高斯和的性质，可参考文献[1-3，12-13]。

1 定理及推论

定理1设p为奇素数，对任意非负整数m和n，有等式

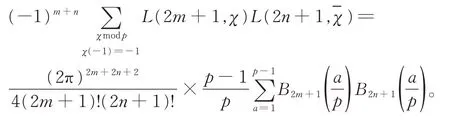
定理2对任意整数n≥0，有等式

取m=n=0，由及定理 1，可以推得文献[1]中的公式。

取m=1，n=0，由定理1及B3(x)=x3-可得到

推论1设p为奇素数，有

取x=0 和对于任意正整数n，有

且

由定理2 还可得到以下5 个推论。

推论2对任意整数n≥0，有

推论3对任意整数n≥2，有

推论4对任意整数n≥1，有

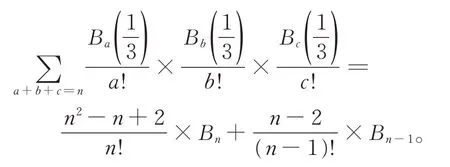
推论5对任意整数n≥2，有

推论6对任意整数n≥1，有

作为推广，本文还获得了与DirichletL-函数相关的2 个简单结果：

定理 3假设q和n是正整数，q＞ 1，n≥ 3，χ为模q的任意偶的原特征，那么有恒等式

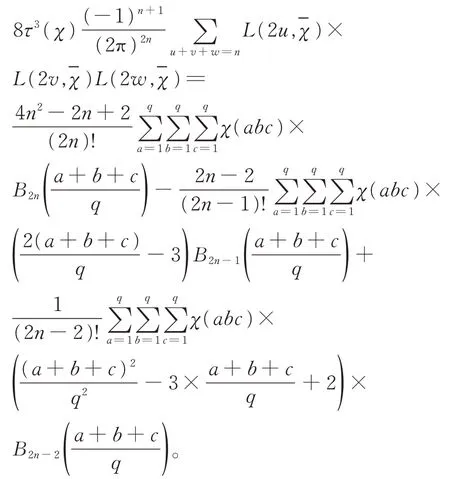
定理 4假设q和n是正整数，q＞ 1，n≥ 0，χ是任意模q的奇的原特征，那么有恒等式

定理3 和定理4 的结果并不完美，它们只是一次尝试。事实上，如果可以将这2 个定理的右边表示为一些特殊的L-函数，那么这2 个定理会更加完美，但需做进一步简化。

2 引 理

为证明本文的定理，需要以下3 个简单的引理。

引理1令则有等式

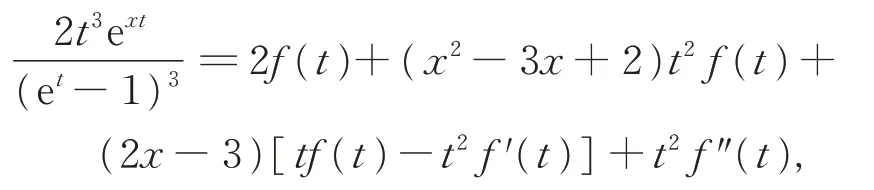
其中f'(t)表示f(t)关于t求导。

证明由f(t) 关于t求导的定义可得

结合式(5)、式(6)以及f(t)的定义，可得等式

引理1 得证。

引 理 2设q＞1为正整数，χ为任意模q的 原特征。若χ为偶特征，即χ(-1) =1，那么有

若χ为奇特征，即χ(-1) =-1，那么有

其中τ(χ)为经典高斯和。

证明由伯努利多项式的生成函数(3)可得

如果χ为模q的原特征，且是偶特征，即χ(-1) =1，则有

对任意整数n，如果n=1且0＜x＜1，或者n≥2，0≤x≤1，那么由文献[1]定理 12.19，可得

由式(9)以及经典高斯和的定义和性质得

由式(10)以及经典高斯和的定义和性质得

若χ是模q的原特征，且是奇特征，即χ(-1) =-1，由式(11)和式(12)的证明方法，可得

如果χ为原特征且是偶特征，那么由式(7)、式(8)、式(11)和式(12)，有

如果χ为模q的原特征且是奇特征，那么由式(7)、式(8)、式(13)和式(14)以及等(15)的证明方法，有

由式(15)和式(16)，便可得到引理2。

引理2 得证。

引理 3设q为正整数且q＞ 1，χ为模q的任意本原特征，那么有等式：

3 定理的证明

先证定理1。对于任意整数n≥0，如果χ是模p的偶特征，那么有

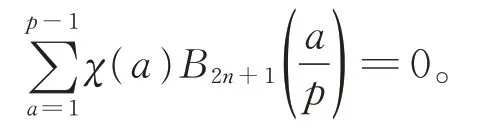
由模p的正交性特征，有

由式(14)、式(22)及式(23)，可得恒等式

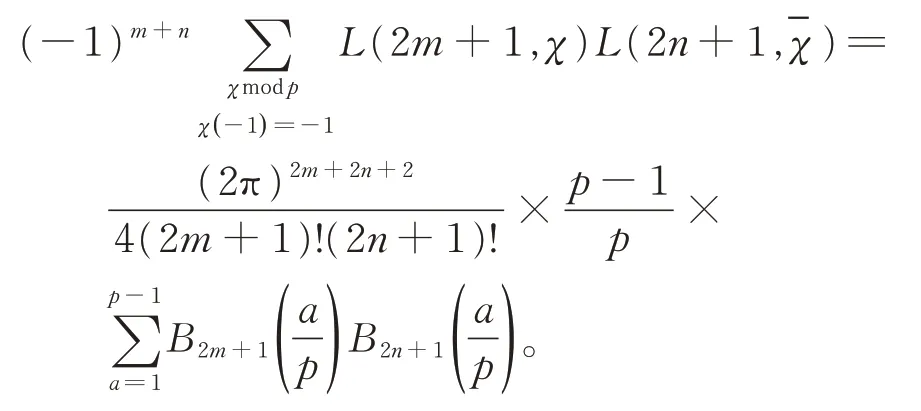
定理1 证毕。

由式(3)和引理1，通过比较幂级数系数，可推得定理2。

下证定理3。如果χ为模q的偶特征，那么由引理 2、式(17)～式(21)，通过比较引理 1 中幂级数的系数，有

定理3 证毕。

再证定理4。如果χ为模q的奇特征，那么由引理 2、式(17)～式(21)，通过比较引理 1 中幂级数的系数，可得

定理4 证毕。

4 结 论

本文的主要结果是4 个定理。定理1 得到一个新的关于素数模p的DirichletL-函数的平方均值公式 ，当m=0，n=1 或m=1，n=0 时 为 DirichletL-函数的一个非常有趣且美观的平方均值公式。定理2 证明了一个包含伯努利多项式的新等式，特别是推论3 和推论5，十分简洁美观，是有关伯努利数或黎曼ζ 函数的新结果。定理3 和定理4 给出了DirichletL-函数卷积和的2 种新表达式，揭示了L-函数之间的关系。但此2 定理看起来并不简单美观，需要进一步简化和改进，如果可以将这些定理中公式的右侧表示为一些特殊的L-函数，定理3 和定理4 就会更加完美。