重型车辆悬架用变丝径螺旋弹簧研究

张军伟，万 芳，吴学雷，佟家慧，齐 鸣，乔 杰

（北京航天发射技术研究所，北京 100076）

车辆悬架用螺旋弹簧是连接车架和车轮的关键部件，可以缓冲路面不平度对车架造成的冲击，关系到整车的行驶平顺性和操纵稳定性。螺旋弹簧具有结构紧凑、质量小、能量密度高、结构灵活等优点，在乘用车领域得到广泛应用[1-3]。

重型特种车辆具有行驶路况复杂、轴荷大、轮跳行程大的特点，用于重型特种车辆的螺旋弹簧在具备高承载能力的同时还要满足轮跳行程的需求，以及考虑压并稳定性及疲劳寿命指标[4]。

本研究针对某重型特种车辆，在布置空间有限、载荷大、轮跳行程大等约束条件下，设计了一种变丝径螺旋弹簧，在达到承载能力的同时还满足了行程需求。推导了变丝径螺旋弹簧压并载荷、等效刚度计算方法，并用台架试验验证了理论计算的准确性。

1 设计输入及要点

重型特种车辆轴荷大，需要匹配的螺旋弹簧刚度也较大，若使用等刚度螺旋弹簧在既满足刚度参数又满足行程需求的约束条件下，必然导致螺旋弹簧自由高度增大和高径比增大，大的高径比会降低螺旋弹簧压缩过程中的抗弯稳定性，从而引起失稳甚至断裂[5]。

基于重型特种车辆对螺旋弹簧大刚度、大行程、低高径比的需求，采用变刚度螺旋弹簧方案。变刚度螺旋弹簧主要有3个影响因素：丝径、中径、节距。为了便于热卷加工，一般采用等内径设计，中径随丝径而变化，则变刚度影响因素减为两个：丝径和节距。当需要刚度较大，且行程不太大时，可采用等丝径变节距方案，当需要刚度较大，且行程也较大时，采用变丝径变节距方案。针对该重型特种车辆载荷大、轮跳行程大的特点，采用变丝径变节距螺旋弹簧方案[6-7]。变丝径螺旋弹簧设计输入见表1。

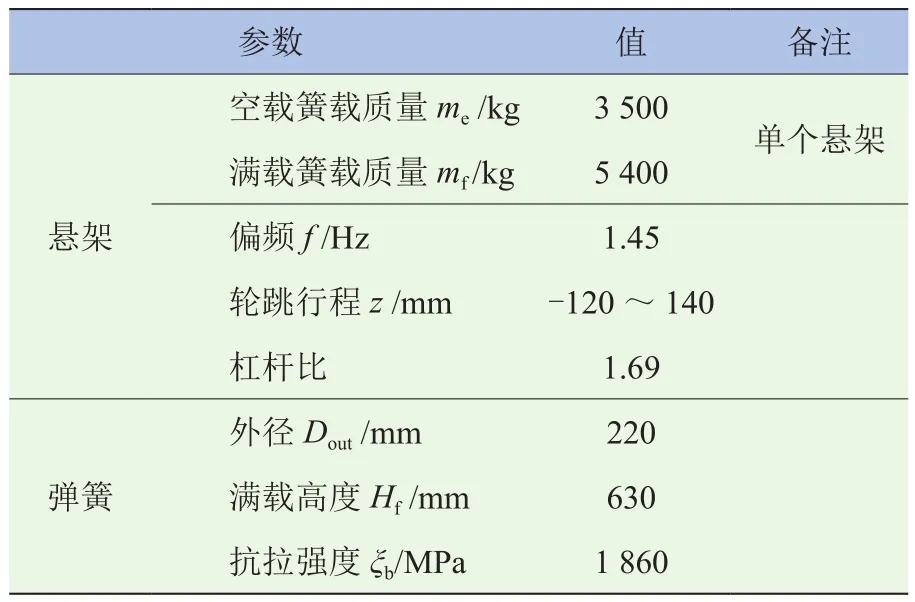
表1 设计输入

由表1可知，用簧载质量和偏频确定螺旋弹簧刚度；用轮跳行程和杠杆比确定螺旋弹簧压缩和伸张行程；用三维布置确定螺旋弹簧外径和满载高度；外径和满载高度是螺旋弹簧参数设计的约束条件；材料抗拉强度用于螺旋弹簧强度校核和疲劳寿命计算。

2 理论计算

变丝径螺旋弹簧物理结构分为3段：上端变丝径段、中间主段、下端变丝径段。其中，上端变丝径段和下端变丝径段以弹簧长度中心对称；中间主段的丝径d、节距t都固定，可认为中间主段为定刚度，可按常规公式计算其参数；变丝径段弹簧丝径从d0变化至中间主段丝径d，节距从t0变化至中间主段节距t，如果两端是磨平并紧结构，则支撑圈与变丝径第1圈有效圈的节距为0。

中间主段可按常规定刚度弹簧公式计算，重点对变丝径段的丝径、节距、压并载荷、压并应力等参数的计算方法给予说明。

变丝径段共n圈，丝径从d0至d为均匀渐变过程，对应的中径从D0至D也是均匀渐变过程，其遵循线性变化规律，第k圈的丝径、中径计算如式（1）所示。

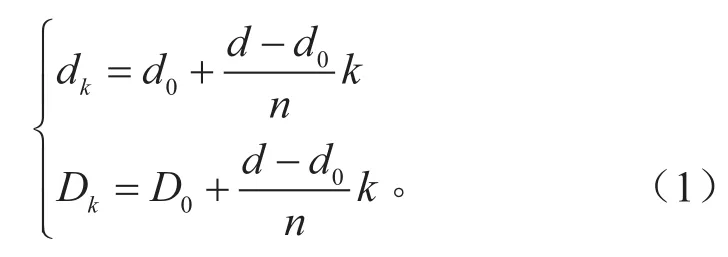
式中：d0为变丝径段起始丝径；d为变丝径段末端丝径，即中间主段丝径；n为变丝径段总圈数，包括有效圈数nc和支撑圈数nz；D0为变丝径段起始中径。

变丝径段第k圈与第k-1圈的节距计算如式（2）所示[8]。

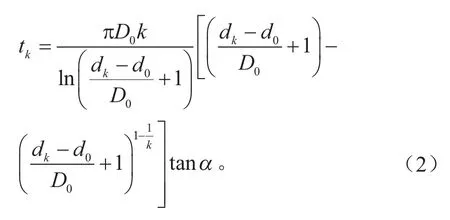
式中：tk为变丝径段第k圈的丝径；α为螺旋角。

变丝径段第k圈的压并载荷计算如式（3）所示[9-10]。

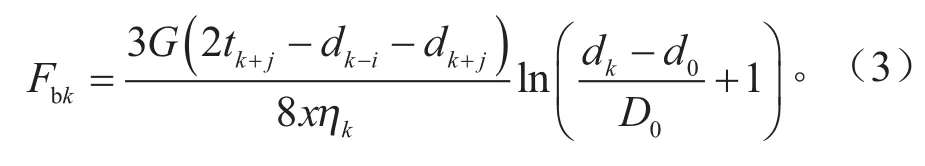
式中：Fbk为变丝径段第k圈的压并载荷；G为材料剪切模量；当圈数k为整数时，i=1，j=0，x=1；当圈数k为非整数，取0.5、1.5、2.5等形式的小数时，i=0.5，j=0.5，x=2；ηk为变形系数。其中，变形系数ηk由式（4）计算得到。

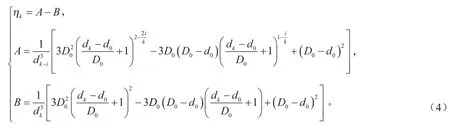
式中：A、B为计算中间变量。

用压并载荷计算变丝径段第k圈在压并载荷下的轴向变形量，如式（5）所示。

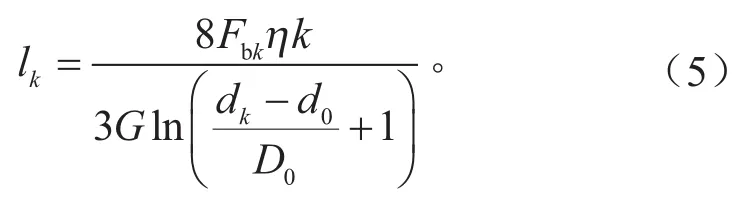
式中：lk为变丝径段第k圈在压并载荷下的轴向变形量。

用压并载荷以及压并载荷下的轴向变形量计算变丝径段压并圈的等效刚度，式（3）和式（5）可得等效刚度计算，如式（6）所示。

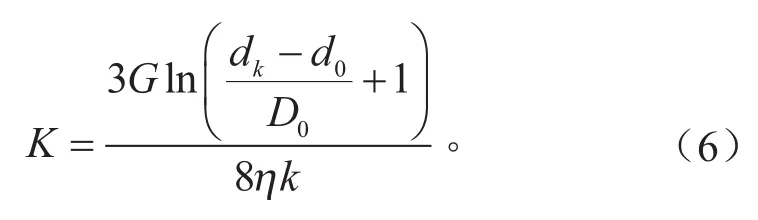
式中：K为变丝径段压并圈的等效刚度。

剪切应力计算如式（7）所示。

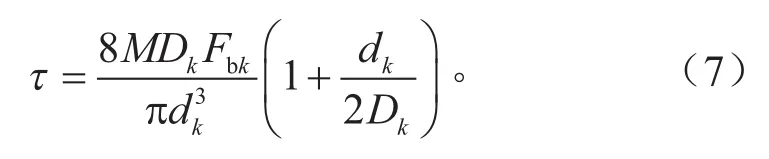
式中：τ为剪切应力；M为载荷系数。

静载荷系数和动载荷系数计算如式（8）所示。

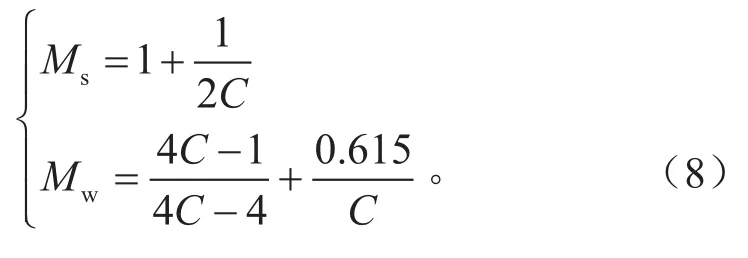
式中：Ms为静载荷系数；Mw为动载荷系数。

根据表1的设计输入，计算变刚度螺旋弹簧设计参数见表2。变丝径段的丝径，从初始值以线性规律变化至中间主段值，变丝径圈每一点的刚度为逐渐增大的过程。在弹簧受压时，变丝径段从有效初始圈（对于两端磨平并紧的结构，有效圈从0.75圈开始算起）每一点逐渐被压并成为支撑圈，被压并成为支撑圈的弹簧将不再承受剪切力。

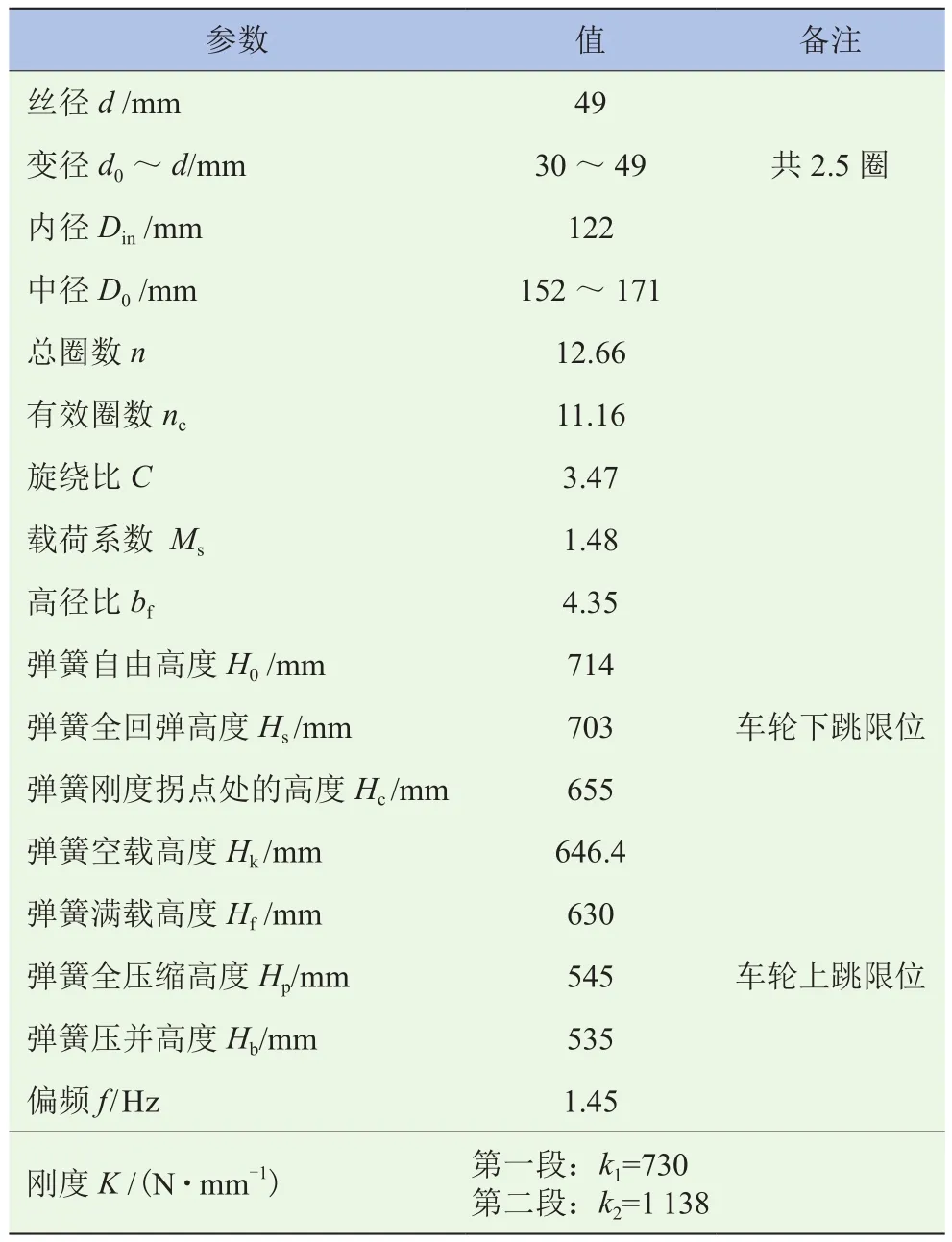
表2 变丝径螺旋弹簧设计参数

由于弹簧设计时将刚度拐点设计在满载之前一定行程的位置，所以在满载、全压并两种状态，不必考虑已压并的变丝径段的应力，只需计算中间主段的应力。变丝径段各圈、中间主段在各种工况下的应力见表3。

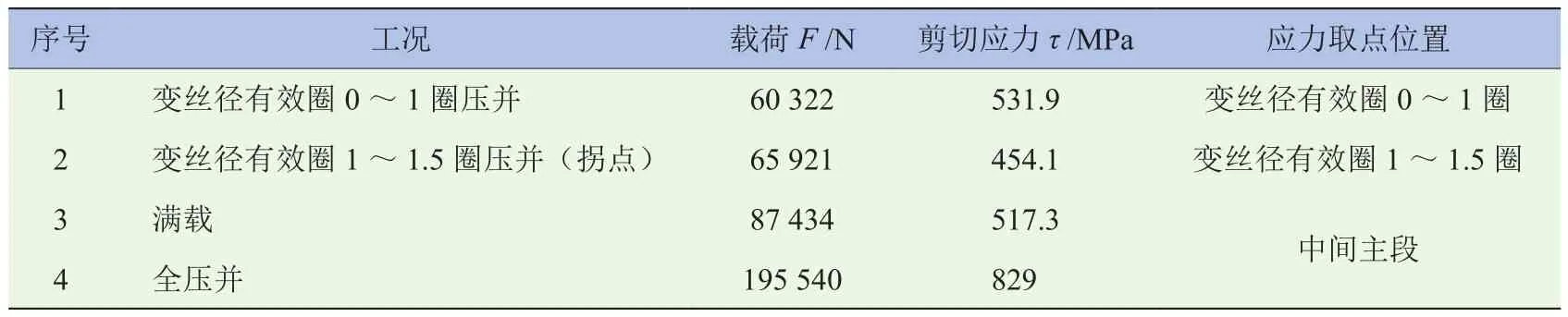
表3 应力计算结果

变丝径螺旋弹簧弹性力与压缩量的关系曲线如图1所示，横坐标为螺旋弹簧在自由状态时的压缩量。弹性力曲线拐点处，变丝径段压并成为支撑圈。拐点之前，变丝径段未全部压并，弹簧拐点之前的刚度（曲线斜率）等于变丝径段刚度与中间主段刚度的串联，因此，弹簧在拐点前的刚度较小一些。拐点之后，变丝径段被完全压并，变成支撑圈，弹簧受外界力再继续压缩时，只有中间主段的弹簧在起作用，弹簧在拐点之后的刚度等于中间主段的刚度，因此，弹簧在拐点前的刚度较小一些。

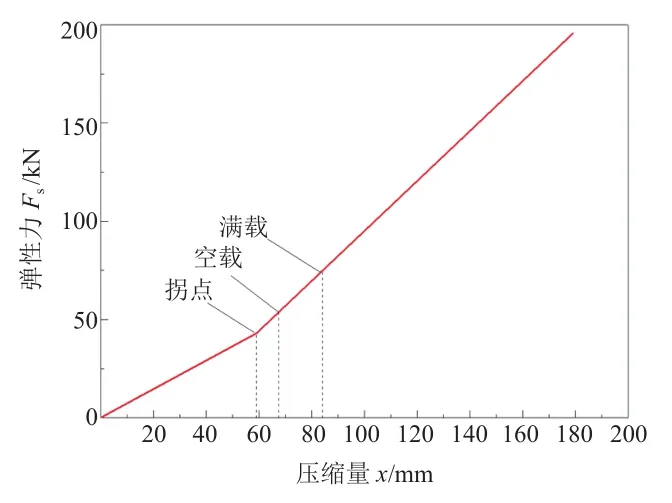
图1 变丝径螺旋弹簧弹性力-压缩量曲线

刚度拐点设计在空载、满载位置之前，拐点与满载位置的行程距离有25 mm，可保证车辆满载状态在较好路面行驶时，弹簧变丝径段一直处于压并状态，避免变丝径段在压并与非压并状态之间频繁转换造成簧丝断裂。

3 台架试验

针对变丝径螺旋弹簧设计刚度特性台架试验，测试弹簧从自由状态至压并状态整个过程中的弹性力与压缩量的关系，用于验证理论计算的准确性[11]。

试验方案如图2所示，作动器固定在龙门架横梁下部，作动器由上而下作动；螺旋弹簧上端支座采用吊耳结构，吊耳内装有关节轴承；螺旋弹簧下端支座固连于地板T型槽。

以位移加载方式，对试验台加入三角波信号，如图3所示。作动器位移为0时，弹簧处于自由状态；当作动器位移缓慢增至179 mm时，弹簧处于压并状态；作动器位移以相同的规律从179 mm减至0，则弹簧从压并状态恢复至自由状态。

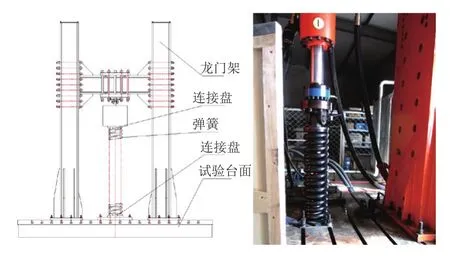
图2 螺旋弹簧台架试验

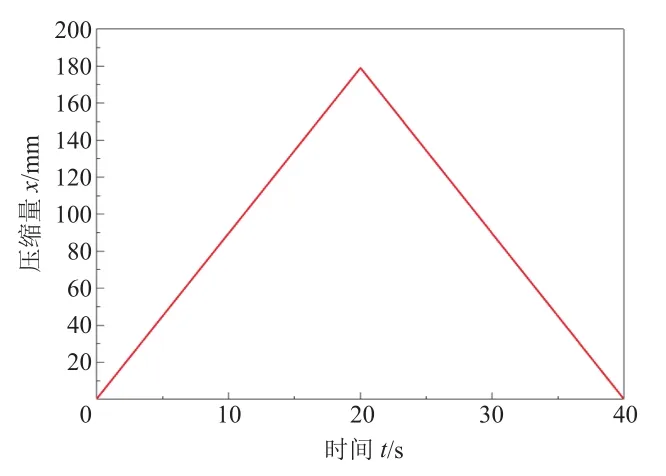
图3 作动器激励信号

在弹簧从自由状态至压并状态再恢复至自由状态的整个过程中，记录弹簧从自由状态至压并状态的作动器位移及输出力，绘制弹性力-压缩量曲线，并与仿真计算结果对比，如图4所示。

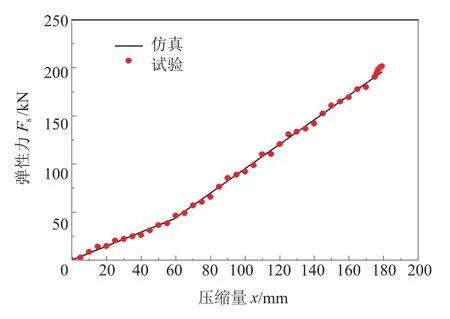
图4 弹性力曲线仿真与试验对比

图4中黑色实线为仿真计算结果，红色点线为试验曲线。由图4可知，仿真计算结果与试验结果整体吻合较好，误差在5%以内，较大的差异点出现在刚度拐点处，这是由于仿真计算是以圈为单位，不能将变丝径段分成无限多的小单元，仿真计算得出的弹性力曲线在刚度拐点处体现出比较明显的转折。

4 结论

本研究通过对重载大行程悬架用变丝径螺旋弹簧的设计，梳理了变丝径螺旋弹簧的设计输入参数与弹簧特性之间的影响关系，总结了在重载、大行程、布置空间有限等约束条件下的设计要点，提出刚度拐点设计在满载位置之前的要点及意义。

针对变丝径部分，将丝径作为线性变化处理，以圈为单位计算了变丝径段每圈的节距、压并载荷、压并应力和等效刚度。

依据总结的设计要点和推导的计算方法，设计计算了一种用于重载大行程悬架的变丝径螺旋弹簧，在布置空间有限的条件下，不仅达到了刚度要求，而且还满足了行程需求，并用台架试验验证了仿真计算的准确性。