基于CFD的变道超车过程气动特性分析

唐洪涛，龙世桀，杨峻程，王 旭

（天津科技大学 机械工程学院，天津 300222）

汽车高速行驶的操作稳定性、安全性和舒适性在很大程度上取决于汽车的气动特性[1]。汽车在路面上行驶的工况越来越复杂，尤其是汽车在高速超车时，车身周围流场不断急剧变化，这不仅严重影响汽车的气动特性，而且会使车辆发生偏移，影响车辆行驶时的稳定性和安全性[2]。

2000年，AZIM等应用实际汽车1/60的模型基于烟雾可视化方法，对超车过程的湍流特性进行了试验[3]，结果表明，干扰车周围的流动结构根据雷诺数的改变而发生显著变化，但是模型比例与真实汽车相差较大，而且可视化方法提供的定量信息很少。2005年，NOGER 等放大了模型尺寸，采用动态试验对两个1/5尺寸的模型进行了超车过程的瞬态模拟[4]，研究表明，纵向间距、横向间距和相对速度都会对车辆的气动力和力矩产生影响，但是模型较为简单，精确程度低。随后在2008年，CORIN等对超车过程进行了数值模拟[5]，发现了相对速度会对超车过程中车辆周围的压力场产生影响，从而使车辆的受力状态发生改变。2013年，BRUZELIUS等基于RANS方法进行了数值模拟[6]，分析了超车过程引起的阻力、侧向力和横摆力矩系数的变化规律。2014年，HOWELL等通过试验的方法研究了小型汽车超越大型卡车时的空气动力学特性[7]，得到了试验数据，并讨论了试验过程的局限性。ALHOMOUD等应用SolidWorks软件设计了小型汽车和大型卡车模型并进行了模拟仿真[8]，探索超车过程中4个不同位置上阻力系数对两车的影响，但是该模拟并不是连续的超车过程，与真实的超车过程有差异。上述研究主要针对直道超车，对实际生活中的直道超车现象具有一定的指导意义。但是，实际生活中更多情况是变道超车，很少有人将变道超车过程中两车的流场变化以及流场中涡的变化与车身受力相结合进行分析。

综上所述，本文基于前人的研究，采用动网格技术[9]和SIMPLE算法[10]对相同车型不同速度、相同车型不同间距、不同车型的变道超车过程进行了数值模拟，得到了相应的压力云图、速度矢量图、流线图以及侧向力等结果，并对侧向力数据进行分析处理，得出变道超车过程不同位置处两车周围流场变化、车身周围束缚涡与流场中自由涡的变化过程，从而解释车身受力状态发生改变的原因，为汽车行驶提供理论建议。

1 基本控制方程

本文选用的汽车行驶速度不超过100 km/h，马赫数约为0.081 7，小于0.3，因此可以认为此时气体是不可压缩的[11]。

连续性方程：

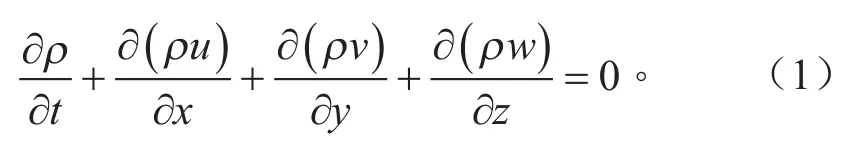
x方向上的动量守恒方程：

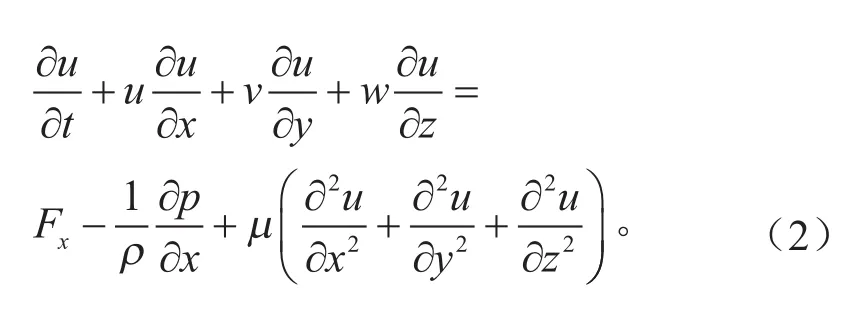
y方向上的动量守恒方程：

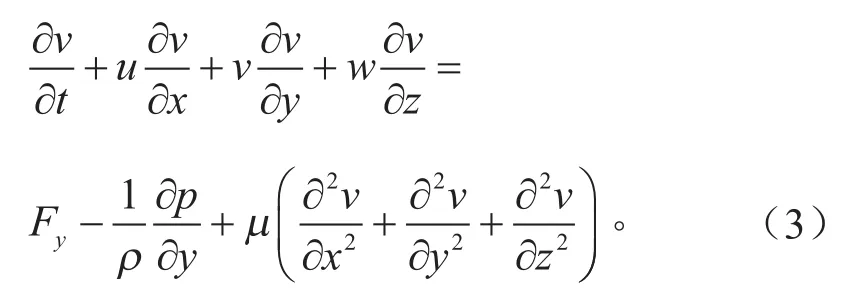
z方向上的动量守恒方程：

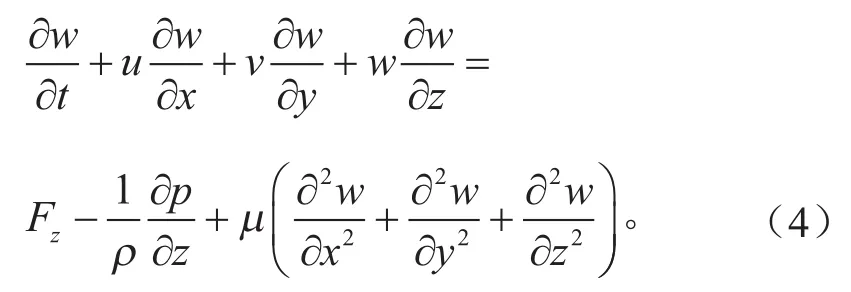
式（2）～（4）中：ρ为密度；t为时间；u、v、w分别表示速度在x、y、z方向上的速度分量；Fx、Fy、Fz分别表示体积力在x、y、z方向上的分量。

标准k-ε模型的湍动能及耗散率运输方程为：

式（5）～（6）中：μi为湍流粘度；Gk是由平均速度梯度引起的湍动能产生项；Gb是由浮力影响引起的湍动能产生项；YM为可压缩湍流脉动膨胀对总的耗散率的影响；C1ε、C1ε、C3ε为经验常数；σk、σε分别为湍动能k和湍动耗散率ε对应的普朗特数，FLUENT中默认值为σk=1.0、σε=1.3；Sk、Sε表示用户自定义源项。

2 数值模拟

2.1 汽车模型的选取和计算域的设定

汽车模型选用某款家用轿车，其基本尺寸为：长4 866 mm，宽1 832 mm，高1 464 mm。按长宽的比例简化为平面矩形，矩形的长用L表示，矩形的宽用W表示，车头与车尾的棱角作光滑处理，两车从右向左行驶，主超车命名为CarA，被超车命名为CarB，两车初始位置距离计算域右边界3L，两车齐头并进。为保证变道超车时两车有足够的行驶距离，且不受两边壁面的影响，计算域尺寸设计为：长30L，宽15W。如图1 所示。

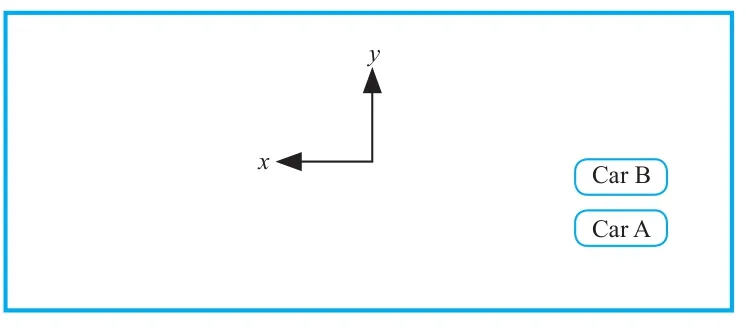
图1 汽车模型和计算域

2.2 网格划分

模拟采用三角形非结构网格，模拟二维变道超车过程，小车车身线的网格尺寸设为0.1，计算域网格尺寸设为0.6。这样的划分方法可以使小车附近的区域网格相对较为密集，而远离小车的区域网格相对较为稀疏，从而可以提高小车周围计算域的精度，更好地完成模拟。如图2所示。

图2 网格模型

2.3 边界条件和初始条件的设定

计算域的右边界设置为压力进口，左边界设置为压力出口，两车车身设置为wall，求解器选用非定常求解器，计算采用k-epsilon湍流模型，定义流体材料中选择ideal-gas（理想气体）。动网格参数的设置选择Smoothing（网格光顺）和Remeshing（网格重划分），Smoothing中的弹性因子设置为0.05[12]。动网格中需要对局部网格进行重新划分，重新划分网格时需要判定网格畸形率和网格尺寸是否符合要求，因此，在Remeshing中选用Must Improve Skewness（改善畸形率）和Size Function（尺寸函数），从而使局部网格完成更好的重新划分，提高网格质量[12]。为了避免动网格计算时出现负体积的问题，网格的最小体积应该大于小车的最快速度与计算步长的乘积。

2.4 变道超车方案设计

记CarA的中心与CarB的中心沿x轴正方向的距离为X，沿y轴正方向的距离为Y，用X/L和Y/W表示两车的位置。变道超车方案见表1。

表1 变道超车方案

3 模拟结果分析

3.1 变道超车压力云图分析

选择Case2的压力云图进行分析。选取超车过程的5个位置，分别是X/L=0.5、Y/W=1.5，X/L=1、Y/W=1.25，X/L=1.5、Y/W=1，X/L=2、Y/W=0.75，X/L=3.5、Y/W=0。单车行驶时，在不考虑侧风的影响下，小车所受的侧向力和旋转力矩几乎为0，但复数车辆变道超车过程中，两车会产生相互影响，图例单位为Pa。

图3 变道超车压力云图

如图3a所示，CarA在x方向上超越CarB半个车身长时，CarA前方的正压区与CarB前方的正压区相互作用，产生不均衡的侧向力。两车之间的区域形成负压区，产生相互吸引的趋势。CarA两侧的气压在短时间内发生剧烈变化，局部受力不均衡，车头内侧压力高于外侧压力，车尾内侧压力低于外侧压力，产生逆时针的趋势，车身发生振动。由于局部受力不均衡，CarB车身内侧压力低于外侧压力，产生逆时针旋转的趋势。此时，CarB的车头有很大几率撞击CarA的车身，属于变道超车过程中的危险位置。

如图3b所示，CarA在x方向上完成对CarB的超越时，CarA内侧气压受到CarB车头处高压的影响，相较外侧呈现高压状态，两侧产生压力差，CarA车身受到内侧指向外侧的侧向力，车尾处内侧区域呈现负压区，受到外侧指向内侧的侧向力，车身产生逆时针旋转趋势，车身振动加剧。CarB内侧气压受到CarA尾部气压的影响相较外侧呈现高压，CarB车身受到内侧指向外侧的侧向力，车头处受到外侧指向内侧的侧向力，车身同样产生逆时针旋转趋势，此时两车容易出现剐蹭现象，因此，两车应该在横向上保持安全距离。

如图3c所示，CarA在x方向上超出CarB半个车身长时，CarA车身内侧仍然受到CarB车头处高压的影响，两侧产生压力差，产生侧向力，随着两车x方向间距的增大，侧向力逐渐减小。同理，CarB的内侧气压受到CarA尾部气流的影响减小，产生的侧向力也随之减小。

如图3d和图3e所示，CarA超越CarB变道至被超车车道的过程中，随着两车x方向间距的增大，两车所受到的侧向力逐渐减小。CarA的尾流对CarB的内侧影响逐渐减小。

3.2 速度矢量图分析

在变道超车过程中，运动的小车周围形成不均衡流动甚至于偏置的流场，两个流场区域相互干涉，不断变化，从而引起小车气动力发生变化。图例单位m/s。

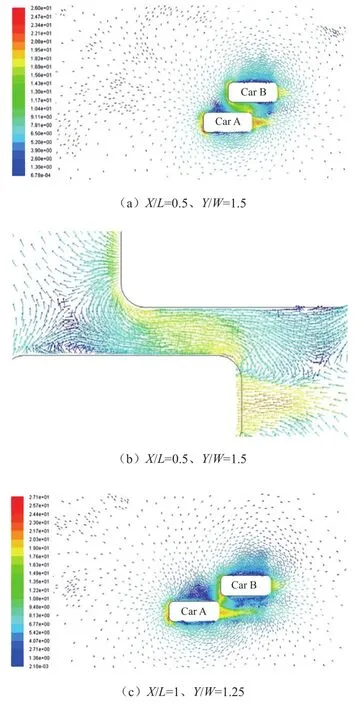
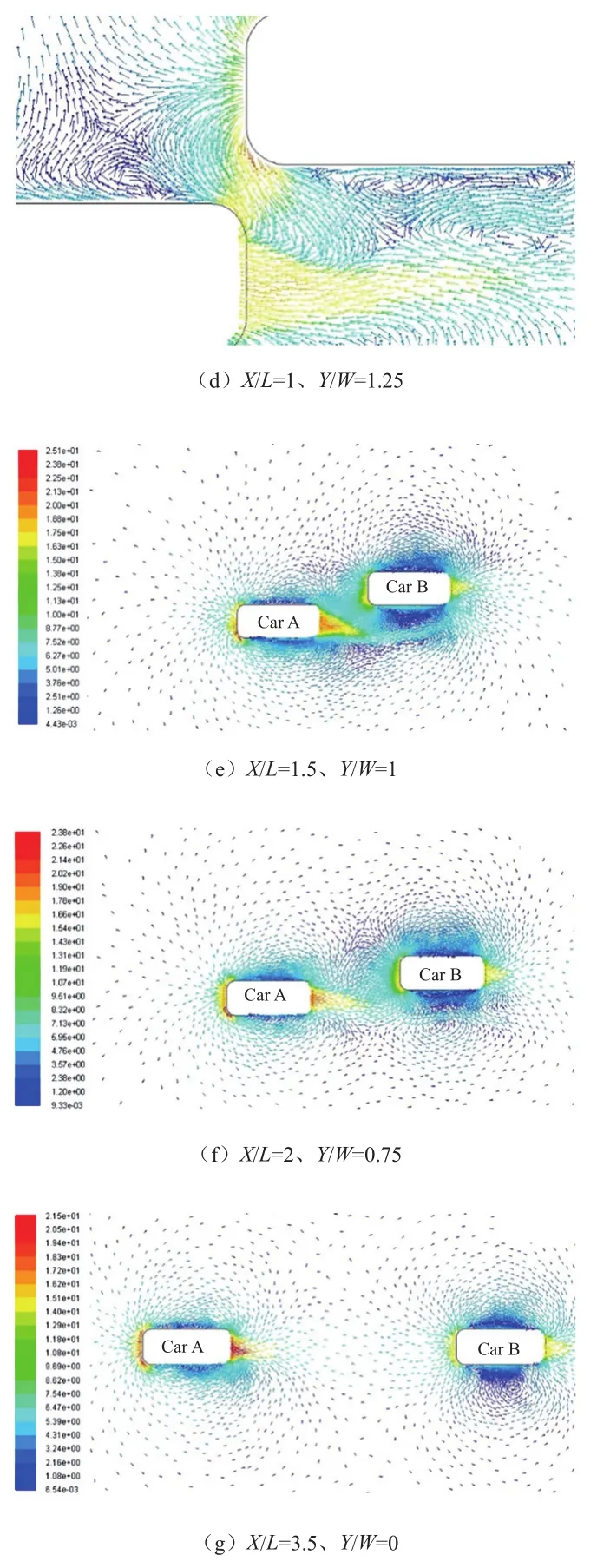
图4 变道超车速度矢量图

图4b为图4a的局部放大图，CarA在x方向上超越CarB半个车身长时，两车之间的区域气流相互干涉，该区域气流明显加速，形成低压区。CarA车身内侧的气流与CarB车头内侧的气流方向相反，相互作用产生排斥力，CarA车头处受到内侧指向外侧的力，车尾处受到低压区的影响，产生外侧指向内侧的力，产生逆时针旋转的趋势，CarA车身发生振动，对驾驶员的操作有很大的影响。CarB车头处受到由外侧指向内侧的力，产生逆时针旋转的趋势。

图4d为图4c的局部放大图，CarA在x方向上完成对CarB的超越，在X/L=0.5到X/L=1的过程中，CarA所受到的侧向力逐渐增大至最大，CarA内侧气流干扰加剧，车身振动加剧。CarB内侧气流受到CarA车尾处气流影响，气流方向、大小都发生了变化，产生涡，由于涡的涡量和位置发生变化，导致CarB车身受力变化明显，对CarB的行驶稳定性造成严重的影响。

如图4e所示，CarA在x方向上超出CarB半个车身长时，随着两车x方向距离的增大，两车的相互干涉减小，CarA受到的侧向力逐渐减小。CarA尾部气流与CarB车头处气流相互干涉，气流加速，在该区域形成低压区。CarB受到的侧向力，同时随着两车x方向的距离增大而减小。

如图4f和图4g所示，CarA超越CarB变道至被超车车道的过程中，随着两车x方向距离的增大，两车流场的相互干涉减小，两车基本恢复单车行驶状态。

3.3 流线图分析

对Case2的流线图进行瞬态流线图采集，时间步长为0.000 1 s，每100个时间步长采集一张图片。通过对比图5所示X/L=0.1到X/L=1.5的瞬态流线图分析发现，从X/L=0.6开始在两车壁面的内外两侧分别出现一对明显束缚涡，随着两车相对位置的变化，束缚涡的涡量发生变化，使两车周围的流场比较紊乱；在CarA的尾流中存在自由涡，这个涡产生、变大、运动、消失的过程，引起两车之间流场相互干涉。

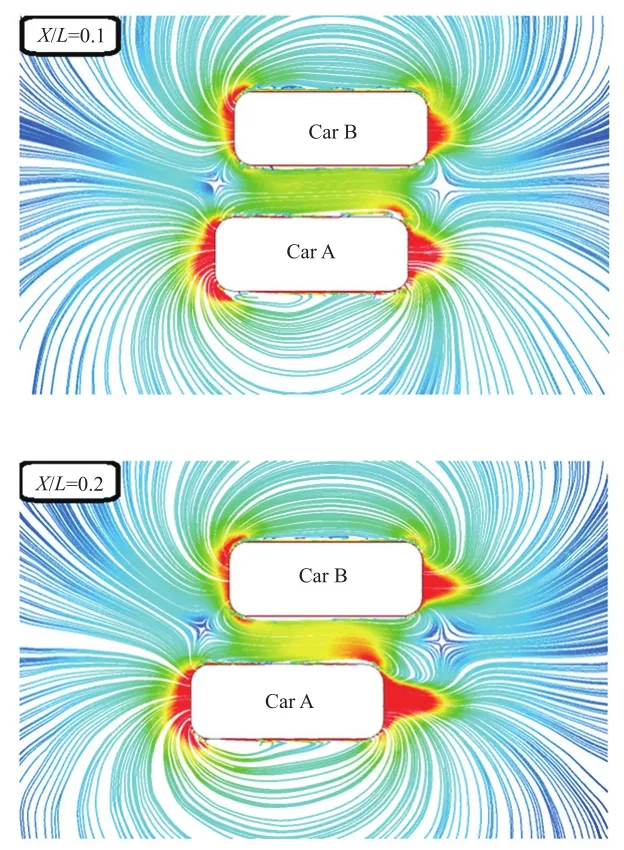
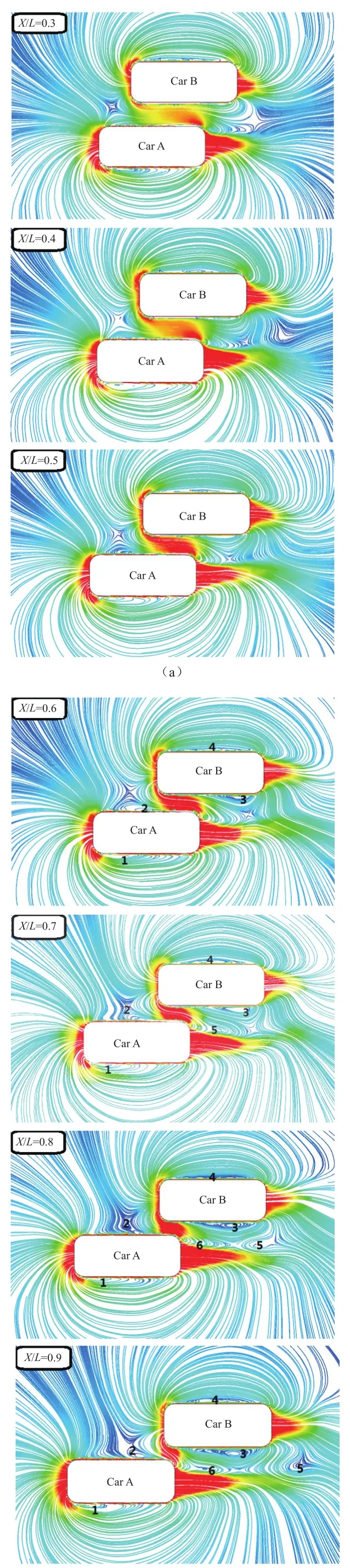
图5 变道超车流线图

在X/L=0.1到X/L=0.5的过程中，两车内侧流线相互作用，气流加速，此处形成低压区，两车产生相互吸引的趋势。随着两车y方向距离减小，两车相互吸引的趋势逐渐增强。在此过程中，两车相互吸引的趋势占主导地位。两车所受到的侧向力逐渐增大，在X/L=0.5时，CarB所受到的侧向力增至最大。

在车身周围循环流动通常发生在车身表面的旋涡称为束缚涡；在车身上形成的循环流动向外侧扩散，并最终消失在大气中的旋涡称为自由涡。

随着两车纵向间距的增大，在X/L=0.6时，存在4个比较明显的束缚涡，分别命名为1、2、3、4涡，其中1涡、2涡在贴近CarA壁面的位置，1涡为逆时针方向旋转，涡尺寸较小，2涡为顺时针方向旋转，涡尺寸较大，3涡、4涡在贴近CarB壁面的位置，3涡为逆时针方向旋转，涡尺寸较大，4涡为顺时针方向旋转，涡尺寸较小。1涡、4涡在CarA、CarB的外侧受到的影响较小，发生的变化也较小。

束缚涡（2涡）的产生、变化消耗流场中的能量，引起周围压强的改变，进而影响CarA的受力状态，同时两车纵向间距增大，低压区范围减小，相互吸引的趋势减弱，因此，CarA受到由内侧指向外侧的侧向力增大。

在X/L=0.7时，2涡涡尺寸增大，3涡涡尺寸增大，5涡是从由2涡脱离车身表面进入大气内形成的自由涡，5涡呈顺时针方向旋转，涡尺寸较小。

自由涡的产生消耗流场中的能量，产生自由涡的位置，压强会发生急剧变化，同时两车相互吸引的趋势减弱，CarB受到由外侧指向内侧的侧向力减小。

在X/L=0.8时，2涡向内侧运动，3涡涡尺寸减小，5涡向后运动，逐渐脱离CarA的尾流流场，涡尺寸增大，呈逆时针方向旋转。

在X/L=0.9时，2涡向后运动，3涡涡尺寸增大，5涡持续向后运动，涡尺寸持续减小，随着5涡从CarA的尾流场中脱离出来，在CarA的尾流场中产生6涡，6涡涡尺寸较小，呈顺时针方向旋转，与5涡旋转方向相反。

在X/L=1.0时，2涡涡尺寸持续增大，3涡向前运动，5涡持续向后运动从捕捉平面消失，6涡向后运动，涡量增大，呈逆时针方向旋转，6涡展现出5涡的特征。

束缚涡涡尺寸、位置的变化过程，引起流场中压强发生改变，束缚涡（2涡）涡尺寸持续增加，位置不断发生变化，对CarA受力状态的影响增大，因此，CarA受到的侧向力不断增加，在X/L=1.0时，侧向力增大至最大。

自由涡产生、变大、运动、消失的过程消耗流场的能量，随着5涡、6涡涡尺寸增大和位置向后运动，对CarB受力状态的影响逐渐增大，在图6b侧向力变化曲线中的表现为CarB所受侧向力的斜率增大。

图6 不同超车速度侧向力变化曲线

在X/L=1.1时，2涡涡尺寸减小，3涡涡尺寸减小，6涡与5涡的运动状态相同，持续向后运动从捕捉平面消失，CarA尾流场中7涡逐渐产生，7涡涡尺寸较小，呈顺时针方向旋转。在X/L=1.2时，2涡涡尺寸增大，3涡向后运动，7涡向后运动，涡尺寸明显增大，呈顺时针方向旋转，7涡呈现出与5涡、6涡相同的特征。在X/L=1.3时，3涡向前运动，涡尺寸增大，7涡持续向后运动，逐渐从CarA的尾流中脱离出来，形成一个独立的呈逆时针方向旋转的自由涡。在X/L=1.4时，3涡消失，7涡持续向后运动，涡尺寸减小，呈逆时针方向旋转。在X/L=1.5时，7涡持续向后运动从捕捉平面消失。随着两车x方向间距增大，CarA的尾流场中不再产生自由涡。

束缚涡（2涡）在X/L=1.1时涡尺寸开始减弱，CarA受到的侧向力逐渐减弱。随着两车纵向间距的增大，两车之间的相互干涉减小，侧向力减小，两车行驶状态逐渐趋于平稳。

自由涡（7涡）在X/L=1.1时产生，X/L=1.2时变大，X/L=1.3时向后运动的过程中，对CarB的影响持续增大。随着自由涡向后运动至车尾处后消失，自由涡对CarB受力状态的影响开始减弱。在图6b侧向力变化图中的表现为：在X/L=1.3附近侧向力趋势发生改变。

通过以上对两车之间流场流线的瞬态仿真分析，在变道超车过程中，高速气流在两车内外两侧壁面位置和两车之间区域变化较为复杂，随着两车相对位置的变化，两对束缚涡的涡尺寸大小持续变化，旋转方向相反。变道超车过程中，CarA尾流场中出现自由涡，自由涡产生、变大、运动、消失的过程，加剧了两车周围流场的相互干涉，因此，研究束缚涡涡量和位置的变化、自由涡从产生到消失的过程对两车受力状态的影响具有重要意义。

3.4 不同车速数据分析

对比分析Case1～3在X/L=0.5、Y/W=1.5位置的压力云图可知，随着两车的速度加快，两车车头处正压值依次增加，相互作用依次加强，两车之间的负压区范围和最大负压值依次增大。因此，在负压区的影响下，主超车和被超车都受到侧向力和旋转力矩的作用，随着两车速度的增加，侧向力和旋转力矩依次增加。

3.5 不同车距数据分析

对比分析Case4、 Case2和Case5在X/L=0.5位置的压力云图可以得出，随着两车的间距增大，两车之间的负压区范围和最大负压值依次减小。随着变道超车的间距变大，主超车和被超车所受到的侧向力和旋转力矩依次降低。

图7 不同超车速度压力云图

图8 不同超车间距压力云图

3.6 侧向力数据分析

3.6.1 不同车速的变道超车数据分析

本文中侧向力的方向是垂直于小车行驶方向的力。在单车行驶状态，不考虑侧风影响的条件下，所受到的侧向力基本为0。在变道超车过程中，小车所受到的侧向力有明显的变化，在超车过程中相对位置不同，所受到的侧向力也不同。当侧向力发生剧烈变化时，小车的行驶稳定性会受到严重的影响。

主超车CarA在Case1、Case2、Case3变道车的超车过程中所受到的侧向力如图6a所示，主超车CarA所受到的侧向力先增大再减小后趋于稳定，在X/L=1时侧向力达到最大。 Case2与Case1、Case3对比发现：控制两车间距不变，两车速度越快，侧向力的变化幅度越大。主超车CarA在Case1的极值比Case2的极值增大了56%， Case1的极值比Case3的极值增大了156%，Case2的极值比Case3的极值增大了64%。

被超车CarB在Case1、Case2、Case3变道车超车过程中所受到的侧向力如图 6b所示，被超车CarB所受到的侧向力先增大再减小后趋于稳定，在X/L=0.5时侧向力达到最大；与主超车CarA相似，随着车速的增加，侧向力的变化幅度增大。Case2与Case1、Case3对比发现：被超车CarB在Case1的极值比Case2的极值增大了68%，Case1的极值比Case3的极值增大了199%，Case2的极值比Case3的极值增大了78%。根据数据可知，改变车速变道超车时，被超车受到的影响大于主超车。

3.6.2 不同间距的变道超车数据分析

主超车CarA在 Case2、Case4、Case5变道车超车过程中所受到的侧向力如图9a所示，控制两车车速相同，改变两车间距对侧向力的影响。随着两车间距的增加，主超车受到的侧向力变化幅度降低。主超车CarA在Case4的极值比Case2的极值增大了42%，Case4的极值比Case5的极值增大了74%，Case2的极值比Case5的极值增大了23%。

被超车CarB在Case2、Case4、Case5变道车超车过程中所受到的侧向力如图9b所示，与主超车相同，随着两车间距的增大，被超车受到的侧向力减小。被超车CarB在Case4的极值比Case2的极值增大了18%，Case4的极值比Case5的极值增大了41%，Case2的极值比Case5的极值增大了18%。根据数据可知，改变间距变道超车时，主超车受到的影响大于被超车。

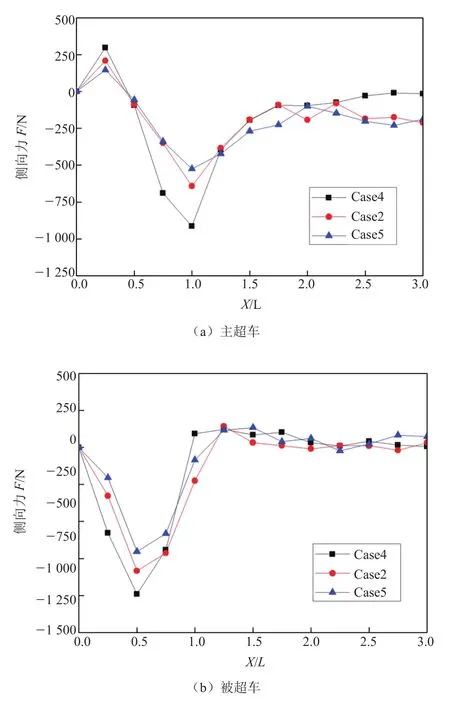
图9 不同超车间距侧向力变化曲线

3.7 不同车型变道超车的分析

3.7.1 小车超越大车

以上是对相似车型变道超车的研究，下面对不同车型变道超车进行探索，对小车超越大车的压力图和侧向力的变化进行分析。该方案命名为Case6，小车命名CarA，大车命名CarB。选取X/L=0.5和X/L=1的位置进行分析。

如图10a所示：不同车型变道超车相较于相同车型变道超车，两车车头处正压区的相互作用明显增大，两车之间的负压区范围和最大负压值有所增大，说明两车相互吸引的趋势增强，侧向力增大。CarB的尺寸和重量较CarA相差较大，侧向力对CarA的影响更为明显，逆时针旋转趋势增强，CarA的操作稳定性受到严重影响，车身出现振动，有很大可能与CarB相撞。

如图10b所示：不同车型变道超车时，两车正压区作用范围明显增强，CarA内侧压力升高，两侧压力差增大，CarA受到的侧向力增加至最大，逆时针旋转趋势增强，CarA的操作稳定性受到影响，车身的振动现象加剧，有一定几率被CarB“吸引”过来，发生车祸。

图10 不同车型变道超车压力云图（小车超越大车）

对比不同车型变道超车的侧向力发现：主超车CarA在变道超车的过程中，所受到侧向力的变化幅度明显增加。主超车CarA在Case6的极值比Case2的极值增大了60%。被超车CarB受到的侧向力也有所增加，被超车CarB在Case6的极值比Case2的极值增大了27%，主超车CarA所受到侧向力的变化幅度更大，对小车的操作稳定性影响更大。

图11 不同车型变道超车侧向力变化曲线（小车超越大车）

3.7.2 大车超越小车

大车变道超越小车的情况，同样对压力图和侧向力的变化进行分析，该方案命名为Case7，大车命名为CarC，小车命名为CarD。同样选取X/L=0.5和X/L=1的位置进行分析。

如图12a所示：不同车型变道超车时，由于CarC的尺寸和质量较大，车头处的正压区范围和正压值较相同车型变道超车明显增大，两车之间负压区范围和负压最大值有所增加。此时CarD所受的侧向力达到最大值，对CarD的操作稳定性有很大的影响，有很高机率与CarC相撞。因此，应控制两车保持安全的距离。

如图12b所示：不同车型变道超车相较于相同车型变道超车，两车的车头处正压区的相互作用明显增强，CarC的内侧压力增大，导致两侧压差增大，此时CarC受到的侧向力也增加至最大，车身振动加剧，对CarC的操作稳定性造成影响。因此，CarD应增大与CarC的间距，降低行车速度，避免发生事故。

图12 不同车型变道超车压力云图（大车超越小车）

当大车超越小车时，两车变道超车过程中，各个位置所受到的侧向力明显增大。主超车CarC在Case7的极值比Case2的极值增大了94%，被超车CarD在Case7的极值比Case2的极值增大了47%，主超车CarC所受到的侧向力变化幅度增大，对大车的操作稳定性影响增大。由于变道超车过程中车型的不同，两车所受的侧向力变化幅度增大。

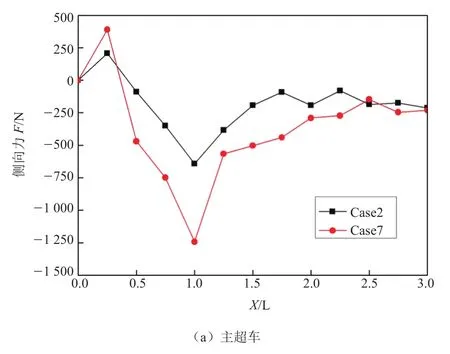
图13 不同车型变道超车侧向力变化曲线（大车超越小车）

4 结论

（1）变道超车过程中压力、速度、侧向力随着两车的相对位置的变化而变化，两车所受侧向力都会先增大后减小，然后趋于稳定，主超车在X/L=1时，侧向力达到最大值，被超车在X/L=0.5时，侧向力达到最大。

（2）变道超车过程中，汽车的行驶稳定性与侧向力的大小有密切的联系，在X/L=0.5到X/L=1的位置的过程中，侧向力较大，此时属于变道超车的危险位置。

（3）变道超车过程相较于直道超车过程流场变化更为复杂，变道超车过程中车身两侧的束缚涡涡量大小持续变化，旋转方向相反；流场中自由涡经历产生、变大、发展、消失的过程，消耗流场中的能量，加剧两车周围的流线发生偏置，从而影响两车的受力状态。

（4）通过方案对比发现：变道超车过程中，两车车速增大，侧向力增大，被超车受到的影响大于主超车；两车间距减小，侧向力增大，主超车受到的影响大于被超车。

（5）不同车型变道超车时，侧向力的变化会有所不同，小车超越大车时，小车受到的影响远大于大车，严重影响驾驶员的操作稳定性，为了避免发生交通事故，应降低超车速度，增加超车间距。