基于散乱点的多元样条拟插值逼近阶估计
黄 芳 张永立 范志勇
(焦作师范高等专科学校数学学院,河南 焦作 454000)
为了处理一元模型中的数据拟合,样条函数的理论首先于1946年由Schoenbrg[1]给出,从而使得一元数据拟合得到了有效处理。Strang和Fix[2]将Schoenbrg的结果推广到了多维情形,并利用紧支撑有限次线性组合做逼近。Dahmen和Micchelli[3]证明了换位子的阶数等价于Strang-Fix条件。后续的许多学者研究了多元样条拟插值[4-6], 并且得到了很好的结论。
整数点上的样条函数逼近已被广泛研究,我们的目的是讨论散乱点上多元样条拟插值的逼近性质。为此,我们将讨论散乱拟插值算子 对 的再生性,并且构造了满足本文要求的线性泛函。最后,我们研究了该散乱拟插值的逼近阶。
1. 预备知识
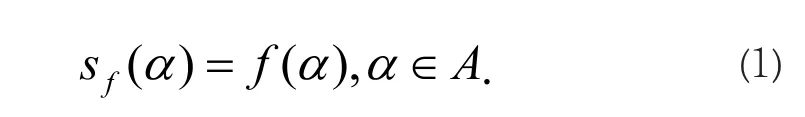

而插值系数 是由插值条件(1)所决定的。这就是说, 需要求解如下线性系统。
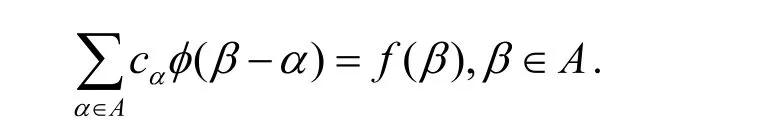
为避免处理大数据时的复杂计算,便引入拟插值:

但是,在许多实际问题中,整数点处的数据是不可得的,或者是存在测量误差的。因此,考虑散乱点上的拟插值问题是很有必要的。给定散乱点集 , 以及对应的函数值表示由 的平移所生成的样条空间,继而给出散乱点上的样条拟插值为

其中,线性泛函为

其中, 是散乱点集 的有限子集。在实际应用中,通常将样条函数 规范化, 即满足:

由于线性泛函仅依赖于 上的点态值,那么拟插值也可写成

考虑 关于连续函数 的换位子

2. 多项式再生性[7]


3. 逼近阶估计
近年来,基于样条函数的拟插值逼近阶估计已被众多学者广泛研究[3,8], 散乱数据的拟插值也在文献[9]中做了一些讨论。在本研究中, 我们借助多元泰勒展开来得到散乱数据多元样条拟插值的逼近阶估计。
为研究多尺度拟插值逼近阶估计的问题, 我们首先考虑由(2)式所定义的拟插值的逼近阶,为此,我们构造最佳近似逼近,事实上:



