基于戴维南等值的系统静态电压稳定极限及稳定裕度快速计算方法研究
安成万 , 郭 星 , 崔曦文
(1.国网山西省电力公司,山西 太原 030012;2.北京科东电力控制系统有限责任公司,北京 100192)
0 引言
20 世纪70 年代后期以来,国际上相继发生多次由于电力系统电压失稳而导致的大停电事故[1-5],这些事故造成了巨大的经济损失和社会影响。随着经济快速发展,电网规模和电能需求与日俱增,快速获得系统电压稳定裕度与稳定极限不仅可以帮助电网运行控制人员及时做出正确的运行控制决策,还对防范电网停电事故和规划电网运行建设有着重大意义。
静态电压稳定分析方法是以系统的潮流方程为基础,通过迭代求解的方法来判别系统的电压稳定性,主要包括连续潮流法、非线性规划法、灵敏度分析法、奇异值分析方法以及潮流多解法等。负荷裕度指标与阻抗模裕度指标均属于静态电压稳定分析指标,可快速有效评估系统静态电压稳定性。
连续潮流法是分析电力系统静态电压稳定的重要方法之一,该算法通过从系统运行的基态点开始不断增加负荷功率来求取最终的电压稳定临界点,由于难以控制增加的负荷步长,使得该算法存在计算效率低且在电压稳定临界点附近难以收敛的问题[6]。戴维南等值方法因其物理概念明确、模型简单且可清晰地表征电压稳定性而成为静态电压稳定性的核心算法之一。文献 [7]定义了阻抗模概念,并基于此提出通过比较负荷节点当前运行状态的阻抗模与其临界阻抗来判断系统电压的稳定性,但并没有提出计算系统阻抗模的计算方法;文献 [8]通过一个具有解析表达式的网络等值电路和方程,对电力系统戴维南等值参数评估问题进行了解析,该方法为解析识别电网中的薄弱节点提供了理论基础;文献 [9]定义了电力系统综合动态阻抗,并基于此提出非解析复变电力系统的动态分析方法,该方法为快速准确计算电力系统极限潮流提供了理论基础;文 献[10]通过基态网络的节点电压和电压灵敏度来求得电网基态和N-1 状态下戴维南等值参数,进而求出节点的阻抗模裕度和最小奇异值,该方法计算过程较复杂;文献 [11]提出戴维南动态等值方法,并基于此提出一种系统临界电压和极限传输功率的计算方法,但可能存在计算过程中迭代次数多而导致计算效率低的问题。
现有的静态电压稳定极限计算与稳定裕度计算的方法存在迭代次数多的问题,且计算效率无法满足当前电网安全稳定运行的要求。为此,本文提出基于戴维南等值的系统静态电压稳定裕度与稳定计算的快速计算方法。以阻抗模裕度指标评判系统电压裕度为基础,提出一种计算送端系统阻抗和受端系统阻抗的快速计算方法,通过比较两种系统阻抗来确定系统电压的稳定裕度;以负荷裕度指标评判系统电压裕度为基础,提出一种基于戴维南等值的系统静态电压稳定极限的快速计算方法。该算法具有计算速度快、准确且直观的特点,对电力系统安全稳定运行控制具有重要意义。
1 静态电压稳定裕度判据
1.1 P—U 曲线
P—U 曲线是一种基本的静态电压稳定分析工具。如图1 所示,P 既可表示某节点的负荷,又可表示某区域的负荷,还可表示传输断面或区域联络线上的传输功率;U 既可表示某负荷节点母线电压,又可表示某区域关键母线电压。通过描绘负荷节点有功功率和电压间的关系,P—U 曲线能够形象地、连续地显示随着负荷增加,系统电压降低乃至崩溃的过程。

图1 负荷节点P—U 曲线
P—U 曲线的上半支是高电压解或可行解,是系统能够稳定运行的平衡点,即联络线输送功率增加会引起负荷节点电压下降,系统能稳定运行;P—U 曲线的下半支是低电压或不可行解,是系统不稳定平衡点,即联络线输送功率减少引起负荷节点电压下降,系统不能稳定运行。基于此,得出的静态电压稳定判据如式(1) 所示。

式中,P 表示负荷节点有功功率或联络线传输功率;U 表示负荷节点母线电压。
当系统负荷逐渐增加,将使得系统运行点从P—U 曲线上半支向下半支过渡,在拐点处系统将失去稳定,为电压稳定的临界点。通过P—U 曲线,可获得评估系统静态电压稳定性的两个重要参量:负荷节点的极限功率和临界电压。
1.2 阻抗模指标
通过潮流有解条件,可得到当负荷节点的等效阻抗等于该节点网络的等效阻抗即系统戴维南等值阻抗时,该网络的输送功率达到极限。因此,可在负荷节点处监视负荷阻抗以及系统的戴维南等值阻抗。当负荷阻抗大于戴维南等值阻抗时,则系统电压稳定;当负荷阻抗小于戴维南等值阻抗时,则系统电压失稳;当二者相等时,则为电压稳定的临界点。
任何复杂电力系统都可通过戴维南等值简化为一个简单的二节点系统,从而快速分析系统的电压稳定性。图2 为戴维南等值电路图,图2 中,USR、ZSR和ZLR分别为系统的等值电势、等值阻抗和负荷等值阻抗,RSR与XSR分别为系统等值阻抗的电阻值与电抗值,RLR与XLR分别为负荷等值阻抗的电阻值与电抗值。

图2 戴维南等值电路图
在系统的运行状态逐渐接近电压稳定临界点的过程中,系统等值阻抗不断增加,负荷等值阻抗不断减小,二者之间的差值将逐渐趋近于0,因此二者的比值可以用来衡量系统的电压稳定性。当负荷增加到使自身的等值阻抗与系统等值阻抗大小相等,就表示系统达到了极限传输功率,当前系统的运行点就对应着电压稳定临界点。
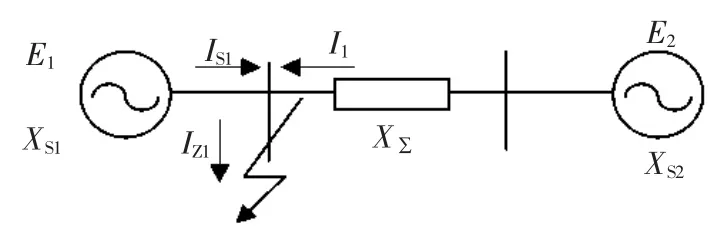
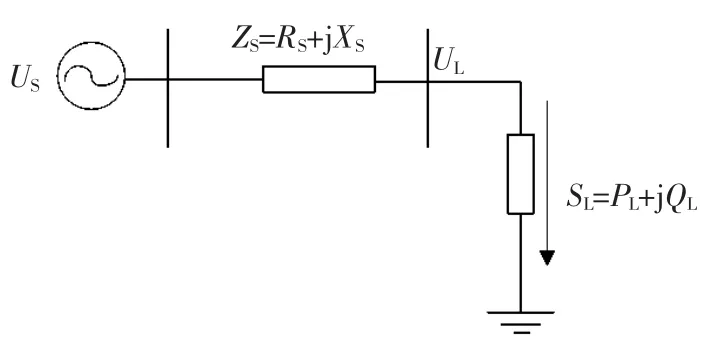
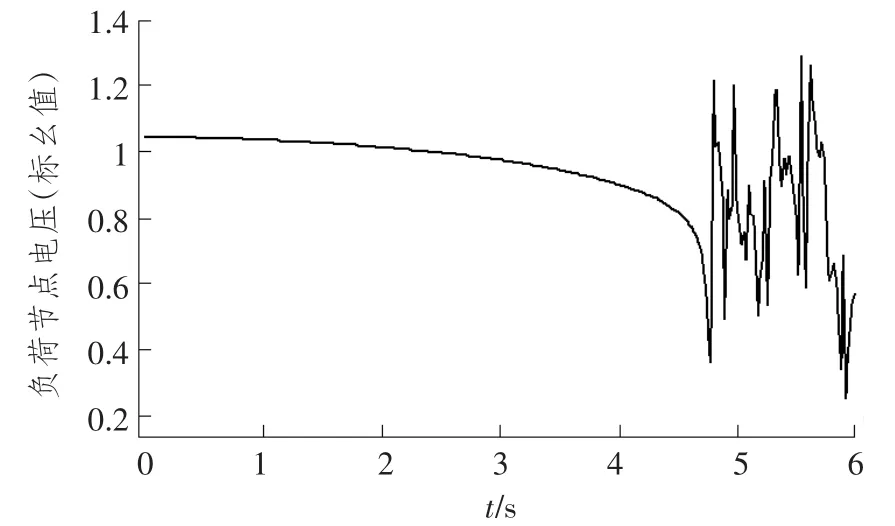
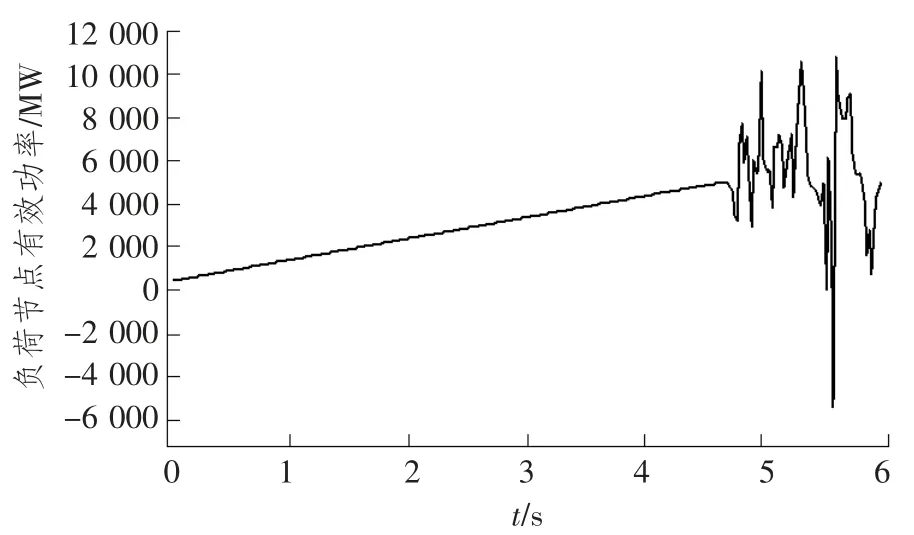
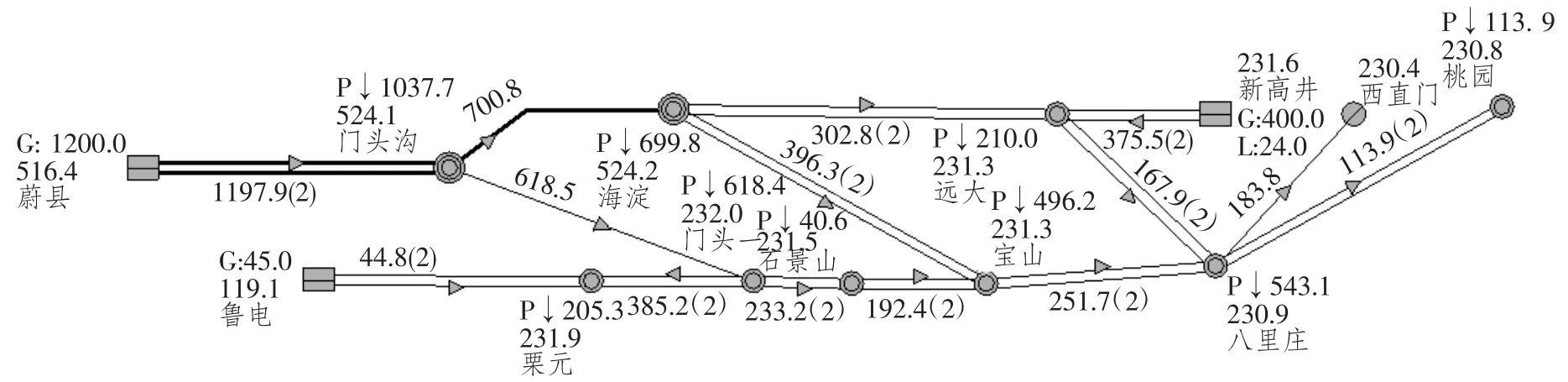
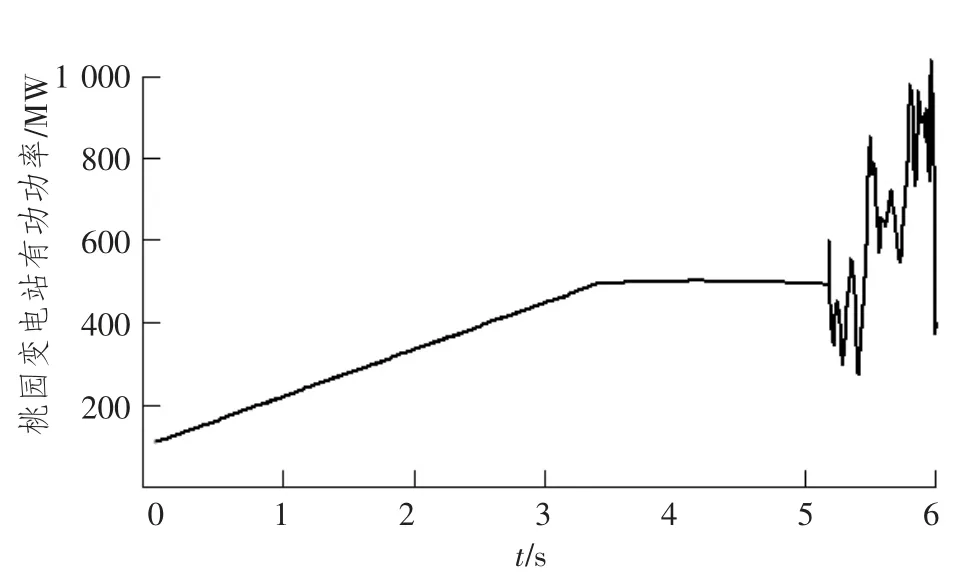
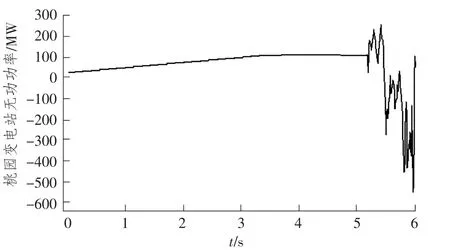
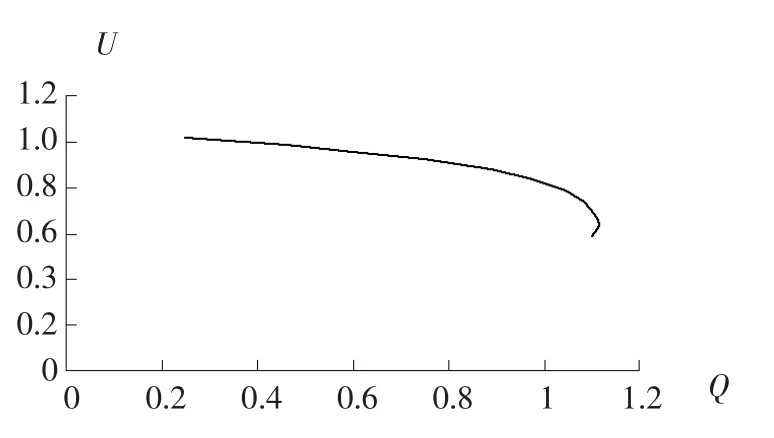
a) 当ZSR b) 当ZSR=ZLR时,即二者的比值等于1,系统的电压是临界稳定的。 c) 当 ZSR>ZLR时,即二者的比值大于 1,系统的电压已经失去稳定。 用阻抗裕度指标来衡量系统的稳定性,其关键是如何获取准确的系统等值阻抗和等值电势。 局部负荷指标是从起始负荷节点功率P0到曲线功率极限值Pmax距离的相对值,如式(2) 所示。 PLmg的值在0 和1 之间,在电压稳定的临界点处负荷裕度为0,即PLmg值越大,该负荷节点的静态电压稳定裕度越大。因此,用负荷裕度指标来衡量系统的稳定性,其关键是如何获取准确的系统负荷节点的极限功率。 戴维南等值原理认为,任意线性系统在任一时间断面都可等值为一个理想电压源经过阻抗向等值负荷节点供电的两节点系统,该两节点系统称为戴维南等值系统。任意时刻j 的戴维南等值系统如图3 所示。 图3 戴维南等值网络 图3 中,ESD和ZSD分别为j 节点等值系统内部的戴维南等值电势和戴维南等值阻抗,统称为戴维南等值参数,RSD与XSD分别为戴维南等值阻抗的电阻值与电抗值;ZLD为负荷侧的等值阻抗,RLD与XLD分别为负荷侧等值阻抗的电阻值与电抗值;SLD为负荷侧的视在功率,PLD为负荷侧的有功功率,QLD为负荷侧的无功功率。 已知两个采样时刻的负荷侧电压相量与电流相量,根据图2 列写的相邻采样时刻的电路方程如式 (3) 所示。 由式(3) 可知相邻时刻内戴维南等值参数如式 (4) 所示。 根据1.2 节所阐述的阻抗模裕度指标可知,系统静态电压稳定裕度计算的关键是获得送端系统的戴维南等值电势与等值阻抗和受端侧等值阻抗,基于戴维南等值原理,利用短路电流来计算送受端系统等值阻抗的快速计算方法。 两个互联区域电网互联等值系统模型如图4所示,设两个等值系统的电压分别为E1和E2,系统的等值阻抗为XS1和XS2(忽略电阻),线路的阻抗为X∑(忽略电阻)。通过对互联系统进行短路计算来获得系统的等值电压与等值阻抗。 图4 区域电网互联等值系统模型 图5 为系统E1侧母线发生三相短路电路图。通过短路电流计算可得到E1侧母线上的短路电流IZ1和联络线上的短路电流I1,由基尔霍夫定律可知等值系统E1侧的短路电流为IS1=IZ1-I1。因此,等值系统E1侧和E2侧的等值电压如式(5) 所示。 图5 系统E1 侧发生三相线路图 图6 为系统E2侧母线发生三相短路电路图。通过短路电流计算可得到E2侧母线上的短路电流IZ2和联络线上的短路电流I2,由基尔霍夫定律可知等值系统E2侧的短路电流为IS2=IZ2-I2。因此,等值系统E1侧和E2侧的等值电压如式(6) 所示。 图6 系统E2 侧发生三相线路图 联立求解式(5) 和式(6),求得两个系统的等值阻抗如式(7) 所示。 基于所提出的送受端系统的等值阻抗快速计算方法,系统静态电压稳定裕度计算步骤如下。 步骤1:根据潮流计算结果,确定互联系统的送受端。 步骤2:利用所提出的送受端系统等值阻抗的快速计算方法求得各系统等值阻抗。 步骤3:比较送受端系统的等值阻抗。若送端系统等值阻抗小于受端系统阻抗,即二者比值小于1,则系统稳定运行,且比值越大,稳定裕度越小;若送端系统等值阻抗等于受端系统等值阻抗,即二者比值等于1,系统临界稳定运行;若送端系统阻抗大于受端系统阻抗,即二者比值大于1,系统不稳定运行。 单机带负荷小系统如图7 所示,US为发电机电势,发电机和输电线路的总阻抗为Zs=Rs+jXs,可记为Zs=|Zs|∠θ;UL为负荷侧电压,SL为负荷侧的视在功率,PL为负荷侧的有功功率,QL为负荷侧的无功功率。绘制的电压向量图如图8 所示。 同一患者的肺部影像表现可出现多种形态、多种分期的结核表现,可出现活动性和非活动性病灶并存的现象,部分复治涂阳患者肺内病灶可有钙化。浸润性病灶及增殖性病灶并存。 图7 单机带负荷小系统图 图8 单机带负荷小系统电压向量图 在图8 中,θ 为发电机和输电线路等效阻抗的阻抗角,φ 为负荷侧等效阻抗的阻抗角。利用电压向量图,根据余弦定理可得式(8)。 将 I=U/|zL|代入式 (8) 可得式 (9)。 根据式(9) 得到的负荷点电压计算公式如式(10) 所示。 根据式(10) 得到的系统送到负荷点的功率如式 (11) 所示。 当dPL/dZL=0 时,负荷点功率 PL为最大值,即 |ZL|=|Zs|时,求得的负荷点最大功率 Pm如式(12) 所示。 根据上述单机带负荷静态电压稳定极限计算方法,结合2.1 节所阐述的戴维南等值定理,本小节提出一种在复杂电力网络内的任意输电线路的静态电压稳定极限快速计算方法。计算方法步骤如下。 步骤一:根据电网网架参数,可知变压器阻抗为Xt,输电线路阻抗为XL,受端负荷SL=PL+jQL,受端电压UL,令基准容量SB与基准电压UB,可计算求出送段送端功率Ss与负荷节点即受端功率因数,计算公式如式(13) 所示。 步骤二:基于戴维南等值定理,对送端变电站进行短路电流计算,可得送端变电站短路容量S,联立的短路容量计算方程与潮流计算方程如式(14) 所示。 式(14) 中,Es与Xs分别表示无穷大电源电动势与内阻抗。 步骤三:根据式(14),可求得送端等效电压源内电势Es与等值系统阻抗Xs,带入式(12),求得的复杂电力网络中所研究输送线路的静态电压稳定极限计算模型如式(15) 所示。 根据1.3 节所阐述的局部负荷指标可知,系统静态电压稳定裕度计算的关键是获得负荷节点的初始有功功率和静态电压稳定极限功率。负荷节点初始有功功率可根据潮流计算结果获得,负荷节点的静态电压稳定极限功率可由2.3 节所提出的快速计算方法获得,再根据式(2),可快速计算出负荷节点的局部负荷裕度指标。负荷裕度指标PLmg值越大,该负荷节点的静态电压稳定裕度越大。 为验证本文所提方法的准确性和适用性,本文以PSD—BPA 为仿真环境,并以单机带负荷小系统和北京地区电网为计算算例来展开仿真研究。 使用PSD—BPA 机电暂态仿真软件,构建的单机带负荷模型系统如图9 所示。发电机1 电抗Xd标公值为0.25,额定功率Pn=5 000 MW,负荷节点初始有功功率P0=500 MW,线路阻抗为0.01。以步长为150 MW 的有功功率增量来增加负荷节点的有功功率,得到的负荷节点的电压与功率随时间变化的仿真计算结果曲线如图10 和图11 所示。根据负荷节点的电压和有功功率仿真结果绘制负荷节点P—U 曲线如图12 所示。由图11 可知,仿真计算所得的负荷节点有功功率极限为5 038 MW。根据2.3 节所阐述的功率极限计算方法,可求得负荷节点的功率极限为5 000 MW,二者的相对误差为0.76%。 图9 单机带负荷系统模型图 图10 负荷节点电压变化曲线 图11 负荷节点有功功率变化曲线 图12 负荷节点的P—U 曲线 以北京地区实际电网为算例,验证所阐述的静态电压稳定极限理论计算方法与仿真计算方法的合理性与准确性。北京地区局部电网潮流图如图13 所示。所选研究区域为八里庄变电站与桃园变电站及其相连线路。根据潮流计算结果,八里庄变电站可视为送端,桃园变电站可视为负荷节点。以桃园变电站初始有功功率的50%为步长来增加桃园变电站负荷有功功率,得到的桃园变电站节点的电压、有功功率与无功功率随时间变化的仿真计算结果曲线如图14、图15 和图16 所示。根据桃园变电站节点的电压、有功功率与无功功率的仿真计算结果,绘制的桃园变电站的P—U、Q—U 以及 S—U 曲线如图 17、图 18 和图 19 所示。 图13 北京电网局部潮流 图14 桃园变电站电压仿真结果曲线 图15 有功功率仿真结果曲线 图16 桃园变电站无功功率仿真结果曲线 图17 桃园变电站P—U 曲线 图18 桃园变电站Q—U 曲线 图19 桃园变电站S—U 曲线 对北京地区电网进行短路计算可知,八里庄变电站的短路容量为S=13 143 MVA,其标幺值S*=S/SB=131.43;根据潮流计算结果可知八里庄变电站送出功率SG=114+j35 (MVA),其标幺值为SG*=1.14+j0.35,亦可知八里庄变电站端电压U=230.9 kV,其标幺值为U*=1.004;根据式(9) 可求得八里庄变电站等效无穷大电源的内电势E=1.056 7 与内阻抗标幺值为XS=0.008 04;根据潮流数据可知桃园变电站的负荷功率SL=112+j24(MVA);其标幺值SL*=1.12+j0.24,亦可知八里庄变电站的变压器阻抗标幺值Xt=0.078 以及线路阻抗XL=0.01;根据式(10) 可求得八里庄变电站与桃园变电站之间线路的静态电压稳定输送极限为标幺值为5.185,由BPA 仿真计算的结果为5 100 MW,其标幺值为5.1,理论计算与仿真计算的相对误差为1.7%,满足工程实践的误差要求。 本文基于戴维南等值原理,考虑阻抗模裕度指标和负荷裕度指标两种静态电压稳定裕度判据,提出系统静态电压稳定极限与稳定裕度的快速计算方法。通过算例分析验证,该方法在计算精度满足工程应用的前提下,能有效提高计算效率,具有一定的工程应用价值。 本文基于戴维南等值原理,首先考虑阻抗模裕度指标提出互联系统送受端的系统阻抗快速计算方法,并基于此提出快速判别系统静态电压稳定裕度的计算方法;其次考虑负荷裕度指标,提出系统负荷节点的静态电压稳定极限快速计算方法,并基于此可迅速计算出负荷节点的负荷裕度指标。该算法具有计算速度快且计算精度可满足工程应用的特点,为电力系统安全稳定运行提供了有力的理论支撑。1.3 局部负荷裕度指标

2 基于戴维南等值的静态电压稳定极限快速计算方法
2.1 戴维南等值原理



2.2 基于阻抗模裕度的系统静态电压稳定裕度快速计算方法


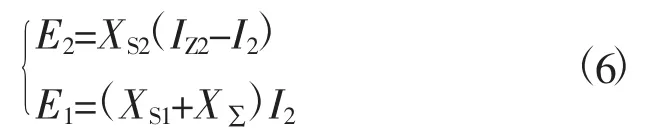

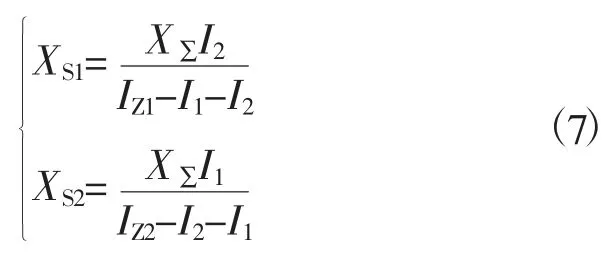
2.3 基于戴维南等值的静态电压稳定功率极限快速计算方法



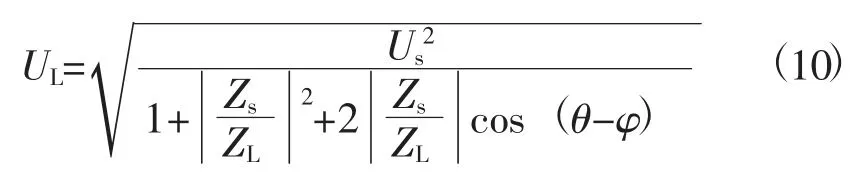
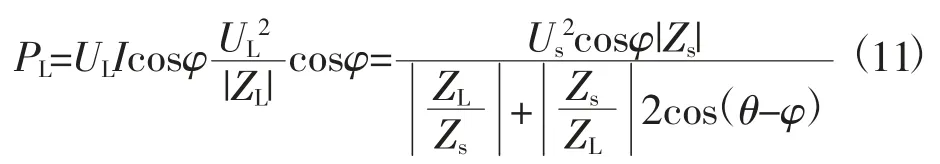

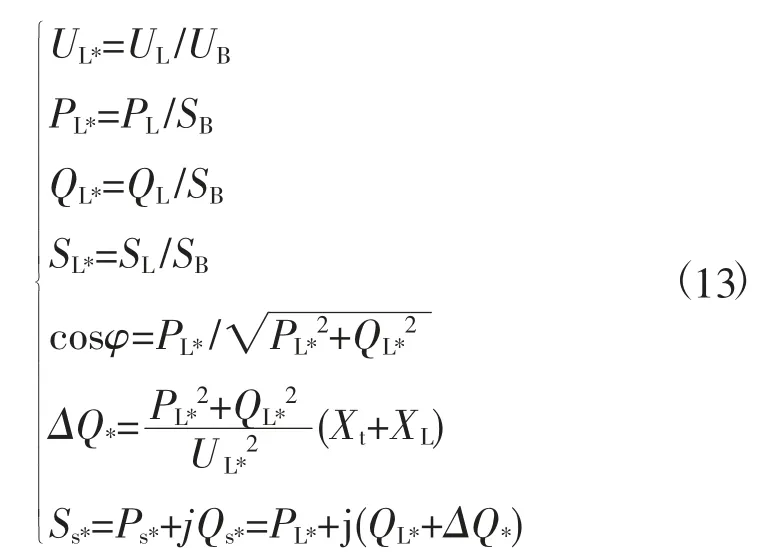
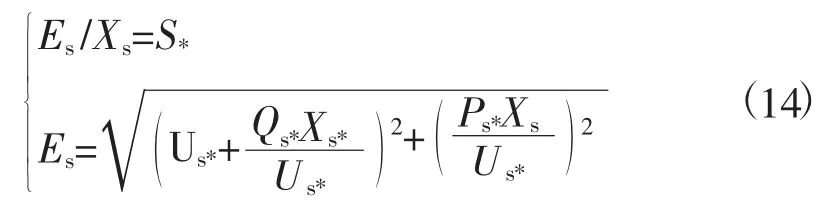

3 算例分析
3.1 单机系统验证


3.2 区域电网算例验证



4 结束语

