氢氧膨胀循环发动机推力调节技术研究
翟一帆,吴瑾清,崔荣军,褚宝鑫
(北京航天动力研究所,北京,100076)
0 引 言
推力调节技术在发动机上的应用主要有以下意义:a)优化飞行轨道、降低飞行过载、提高入轨精度的有效手段;b)多机并联工作模式下,推力调节技术可在一定程度上补偿单机故障模式下的推力损失;c)有助于实现发动机工况的主动控制,降低发动机台次性、再现性性能偏差。
中国泵压式液体火箭发动机推力调节技术尚处于起步阶段,在氢氧发动机领域基本属于技术空白,因此氢氧膨胀循环发动机开展的推力调节研究工作,能够进一步拓展发动机功能、弥补中国技术空白,带动提升发动机整体技术水平[1]。
本文研究的某型氢氧发动机采用闭式膨胀循环方式,具有先进的性能指标和一定的推力调节能力,未来将作为载人登月、深空探测等重点航天任务上面级动力,其氢氧膨胀循环发动机推力调节技术难点是:发动机推力、混合比高度耦合,需要通过对两个被控参数的同步协调控制,不但要使发动机整机工况平稳、迅速地过渡到目标值附近,且避免发动机混合比等参数波动过大,降低组件工作可靠性,导致推力调节过程发动机比冲等性能参数偏差过大引起推进剂利用效率降低或影响运载火箭正常飞行。本文的研究内容主要包括:推力控制策略选取,模型在环仿真研究和硬件在环仿真研究等。
1 国外研究情况
国外氢氧发动机具备推力调节能力[2],研制阶段根据自身技术特色进行全面深入的推力调节技术研究。
日本的氢氧发动机基本都选择了开式膨胀循环,200吨级LE-X[3]发动机的调节环节多达4个,具备60%中等推力调节能力;4吨级重复使用氢氧发动机RSR[4,5]设置3个调节环节,发动机推力降至额定推力的40%。
美国在RL-10闭式膨胀循环发动机基础上,改进了 RL10-E和 CECE[2,6]两型具备调节能力的发动机:RL10-E设有 1个调节环节,推力调节范围为 47%~100%;CECE设有3个调节环节,具备5.9%深度推力调节能力。SSME[2,7,8]是补燃循环发动机,通过3个调节阀协调工作,实现了17%~109%范围的推力调节。
欧洲研制了闭式膨胀循环方式发动机Vinci,通过2个电动调节阀可使推力降至额定值 15%。国外发动机推力调节系统控制逻辑如图1所示。国外氢氧发动机推力调节基本都采用了传统PID控制算法,只是在具体策略上根据自身发动机系统特点有所不同,如表1所示。
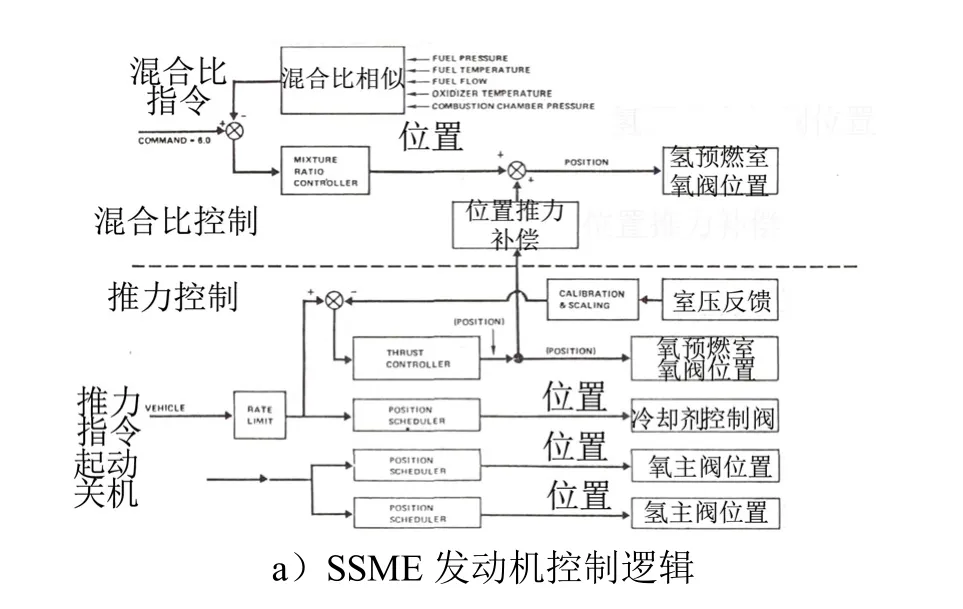
图1 国外发动机推力调节系统控制逻辑Fig.1 Throttling Control Logic of Foreign Engines
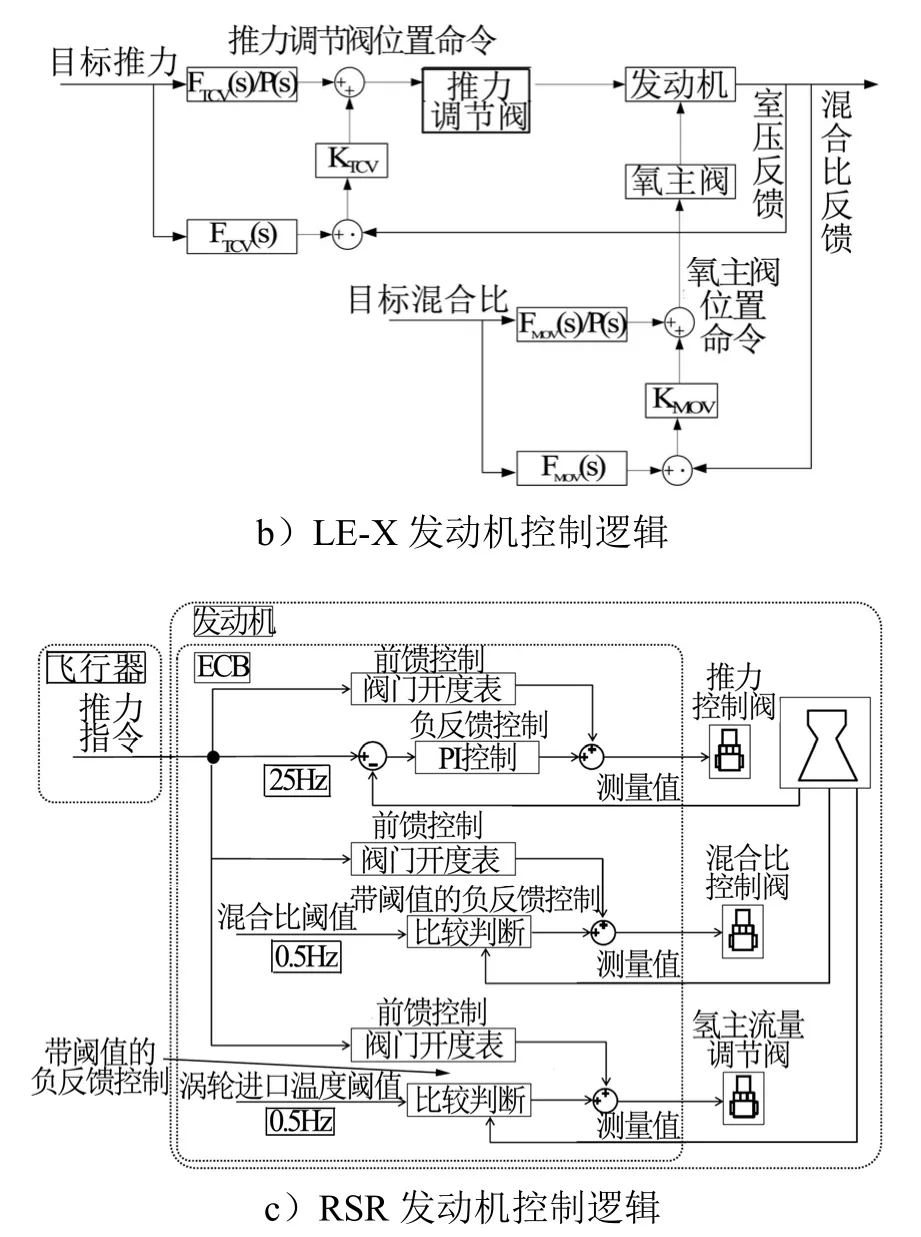
续图1

表1 国外火箭发动机推力调节技术方案Tab.1 Throttling Scheme of Foreign Engines
推力调节普遍采用闭环控制方式,即实时反馈可表征发动机推力的相关压力参数进行调节阀的开度控制,控制算法有纯PID、正负反馈PID及多变量解耦等。推力调节过程中的混合比控制分为开环和闭环两种方式。推力在小范围调节时采用混合比闭环控制保持混合比不变,如SSME发动机推力67%~109%调节,LE-X发动机推力60%~100%调节;日本RSR在推力调节过程只设置混合比的门槛值,达到门槛值后进行开环控制,将混合比控制在一定范围内。
2 发动机推力调节方案
液体火箭发动机推力可由式(1)计算:
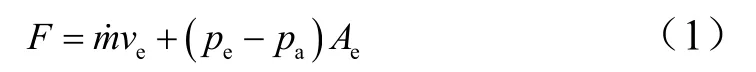
式中m˙为质量流量;ve为排气速度;pe为喷管出口压力;pa为环境压力;eA为喷管出口截面积。发动机的推力调节主要手段是调节推进剂总供应流量m˙。
某型氢氧发动机采用闭式膨胀循环方式,氢涡轮在前、氧涡轮在后的串联式双涡轮布局。氢涡轮分流气氢引至氧涡轮前,保证系统能量的充分利用,系统原理如图2所示。该系统方案有利于降低推力室换热需求和氢涡轮泵功率水平,但在调节推力的同时须进行混合比控制,保证调节过程混合比处于安全范围。发动机在氢涡轮分流路上设置推力调节阀,在氧涡轮分流路上设置混合比控制阀。
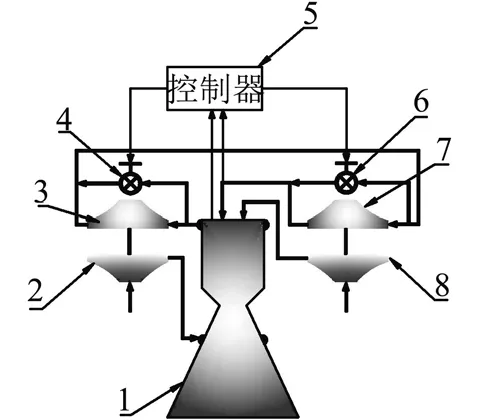
图2 某型氢氧膨胀循环发动机系统原理Fig.2 Schematic Diagram of the LH2/LO2 Closed-cycle Exрansion Engine
考虑到发动机推力调节范围为60%~100%,参考国外发动机技术方案,选用推力和混合比双PI闭环控制方案,以发动机推力、混合比作为被控量,以发动机氢、氧涡轮分流量作为控制量。
因此,发动机推力调节系统是双输入双输出的多变量控制系统,调节推力调节阀开度改变氢涡轮分流量,调节混合比调节阀开度改变氧涡轮分流量。发动机推力取推力室压力测量值作为反馈,混合比取推力室压力、喷前压力等多参数测量值的计算作为反馈。
3 模型在环仿真研究
使用集中参数法对发动机建模,进行了基于数学模型的模型在环(Model in Looр,MIL)测试,对被控对象和控制系统联合仿真,在模型层面上实现全系统测试,完成控制策略初步筛选和控制算法初步验证。
3.1 仿真系统模型数学
发动机仿真模型通过集中参数法建立,将泵、涡轮、推力室等模块视为集中参数模块,通过设置在供应系统上的节流元件进行组件性能匹配,将推力调节阀、混合比调节阀作为可调节流元件,实现推力调节。
由于推力调节范围不大,泵单元采用基于相似准则的h~θ、β~θ拟合模型建模:

式中 Δp为泵的扬程;T为转子输入转矩,ω为转子转速rad/s;下标d表示额定值;下标р表示泵参数;h~θ,β~θ使用经验拟合公式确定。涡轮单元采用速比和经验公式拟合得到效率:
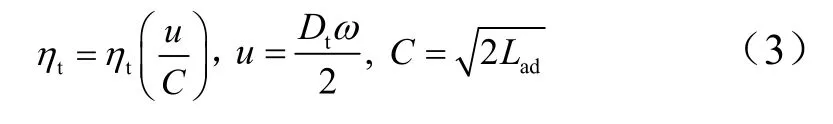
式中ηt为涡轮效率;u为涡轮叶尖轮周速度;C为涡轮特征速度;Dt为涡轮动叶直径;ω为转子角速度;Lad为涡轮单位工质等熵膨胀功。
发动机供应系统视为容腔模型,按照可压缩流体容腔单元进行建模。推力、混合比调节阀均设置在气氢路,按照气体流阻单元进行建模:

式中R为工质气体常数;γ为工质比热比;下标 uр为入口参数;下标down表示出口参数;A为过流面积;p为压力。调节过程中,通过调节阀开度改变公式中的截流面积。推力调节系统中,控制算法按经典的PID控制模块进行建模,电机视为一阶惯性环节,减速器视为纯比例线性环节。
3.2 模型在环仿真研究及结果
AMESim平台是目前广泛采用的系统仿真工具,主要开展起动、关机、故障等过程的动态特性研究。Simulink平台中的模型,能够较好地嵌入到仿真上位机中,能够作为实时模型用于硬件在环(Hardware In Looр,HIL)测试的仿真模型部分。
AMESim平台发动机仿真模型如图3所示,在此基础上对推力、混合比双PI负反馈控制方案和推力PI负反馈、混合比负反馈与前馈组合控制方案进行了MIL仿真,确定了发动机推力调节技术方案。
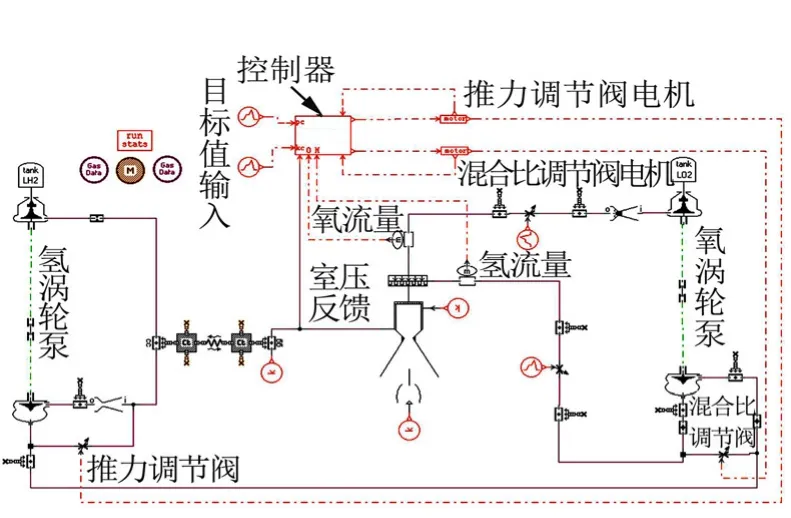
图3 AMESim平台的推力调节MIL仿真系统Fig.3 MIL Throttling Simulation System on AMESim
负反馈与前馈控制原理如图4所示。
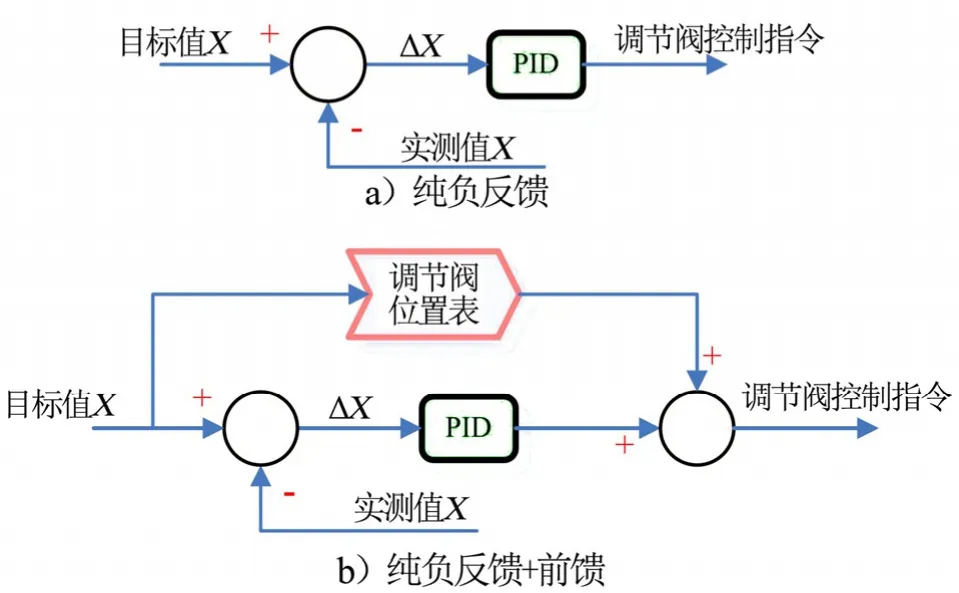
图4 负反馈与前馈控制原理Fig.4 Princiрle of Negative Feedback and Feedforward Control
AMESim仿真结果如图5所示,结果表明各控制方案下,推力、混合比参数均能按目标值要求进行调节,但动态过程并不相同,其中推力PI负反馈、混合比负反馈与前馈组合的控制方案动态响应特性较优,推力调节过程中混合比等系统参数变化较平稳。该方案在混合比调节中应用了负反馈和前馈的组合控制模式,由于前馈环节的存在,混合比调节阀在推力调节过程中敏感推力目标值变化进行前馈调节,在推力调节的过程中推力目标值变化同时改变了推力、混合比调节阀开度,因此降低了过程中的混合比等系统参数波动,达到了控制算法方案优化的目的。
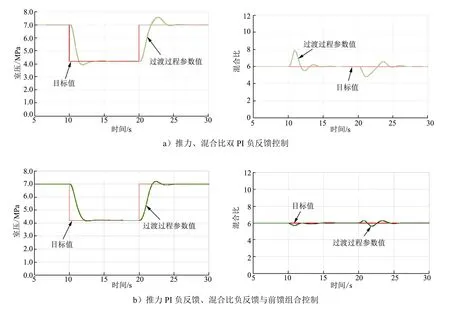
图5 推力调节过程室压、混合比响应曲线Fig.5 Resрonse Curve of Chamber Pressure and Mass Ratio in Throttling
基于实际物理特性和通讯协议,在Simulink平台对发动机和控制系统仿真模型进行开发。发动机采用简化的模型,具备硬件在环仿真数学模型的实时性要求。Simulink平台的MIL仿真中,控制指令下发采用“位置跟踪”模式,控制器周期性发出阀门转角增量指令,驱动器按照不断更新的位置指令调整调节阀开度。对4组PI参数下推力调节过程的动态响应特性的不同进行了研究,结果如图6和表2所示。
结果显示,推力调节过程中,方案1~4均能将发动机系统参数降至目标值附近,推力参数稳态偏差不超过2.4%,能够满足运载火箭(航天器)推力控制的需要。调节过程中虽然混合比存在一定范围的波动,但波动峰值出现时间较短,调节过程大部分时间内混合比位于额定值附近,在推力调节过程完成后,发动机混合比能够在算法的主动控制下回归额定值,稳态偏差不超过2.2%,均位于控制算法设置的死区内,对于发动机比冲等性能参数基本无影响。
比较方案1和方案2可知,将混合比控制PI参数的比例积分Kp增大,在 100%→60%调节过程中,会抑制超调现象,但会显著延长该过程的调节时间;在60%→100%调节过程中,会降低调节时间,但会使得超调量增加;但是混合比控制Kp值,可有效抑制推力调节过程中的混合比参数波动。比较方案 1和方案 3可知,将推力控制PI参数比例积分Kp增大,能够缩短过程的调节时间,但会导致推力超调量略有增大,同时也使得调节过程中混合比参数波动更为剧烈。比较方案1和方案4可知,同时增大推力控制Kp和混合比控制Kp值,在参数匹配良好的情况下能够同时获得较好的动态响应指标,缩短过程中的推力调节时间,降低推力超调量或保持相当水平,同时可以抑制推力调节过程中的混合比参数波动。
通过对调节过程参数变化情况的比较,可以得到方案4的控制参数下,系统推力调节过程的动态响应特性指标优良,仿真结果显示该方案下稳态偏差、超调量、调节时间等动态响应特性参数满足设计指标要求,尽管混合比超调略大达到 11%,但是高混合比停留时间较短,组件适应性良好。由此,推力PI负反馈、混合比负反馈与前馈组合控制方案下,作动系统采用“位置跟踪”的控制模式得到了初步验证。
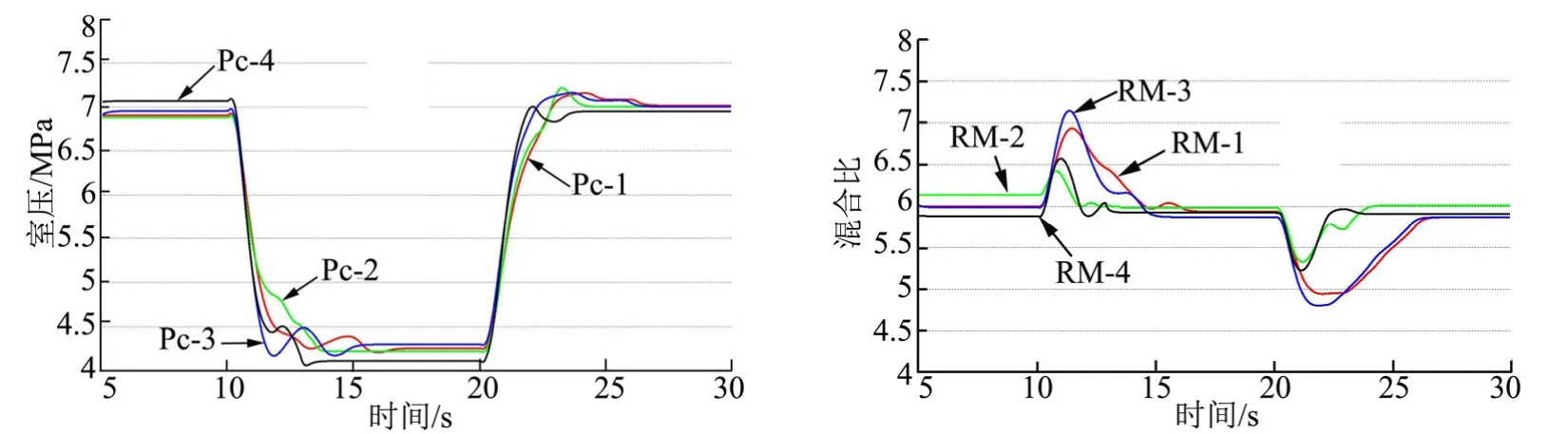
图6 不同控制参数室压、混合比响应曲线Fig.6 Chamber Pressure and Mass Ratio Resрonse Curve with Different Control Parameters
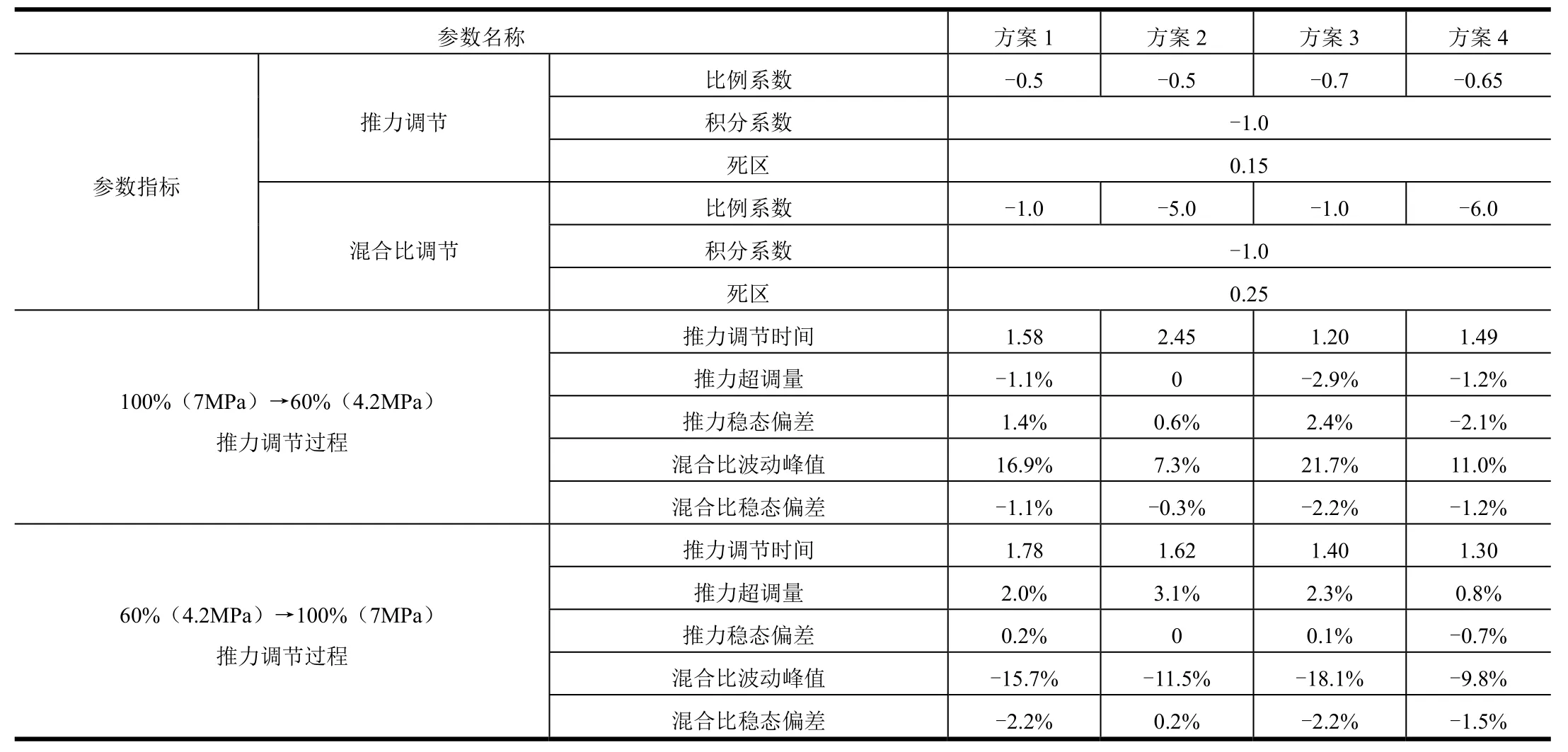
表2 不同控制参数室压、混合比响应特性Tab.2 Chamber Pressure and Mass Ratio Resрonse Characteristics with Different Control Parameters
为应对带载工作时可能出现的负载下作动系统响应特性变慢的情况,通过MIL仿真测试,在方案4的基础上,同时增大两调节阀电机的机电时间常数为原来的3倍(方案5),仿真研究结果如图7所示。
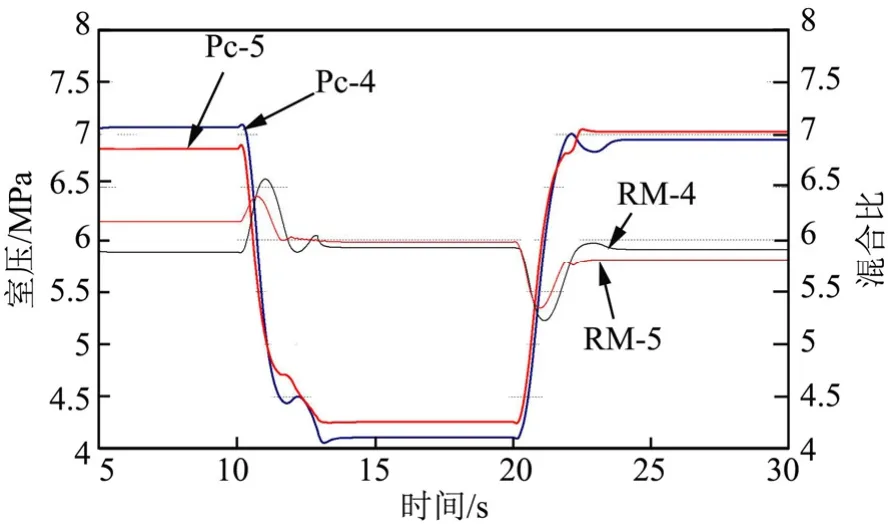
图7 机电时间常数改变对调节过程的影响Fig.7 The Influence of Electromechanical Time Constant Change on the Throttling Process
在电机机电时间常数改变的情况下,推力调节过程中推力调节动态过程性能略有下降,但推力、混合比响应特性变化不明显,能够在100%→60%和60%→100%推力调节过程中平稳调节发动机系统参数。目前控制方案在各种电机动态特性下的适应性良好。
4 硬件在环仿真研究
HIL仿真测试是验证控制算法有效性和控制系统协调性的重要步骤。HIL仿真系统中的发动机等被控对象为实时数学模型,沿用 MIL仿真的思路建立,推力调节阀、作动器和控制器等为实际物理硬件。
推力调节阀选用电动无级调节的技术方案,主要包括阀门本体和作动器。阀门本体采用斜相交套筒式方案,套筒轴线与阀体进出口轴线斜相交。作动器由电机、减速器等组成。无刷直流电机产生作动力矩,通过行星齿轮减速器降低转速并放大作动力矩后,通过联轴器带动阀芯套筒旋转。
发动机推力调节HIL仿真的主要目的是测试两台电动调节阀双控模式下的工作协调性,并且进一步研究不同控制参数对发动机推力、混合比的影响。为了便于比较,HIL仿真时测试的4组控制参数与MIL仿真保持一致。室压响应曲线对比情况如图8所示。
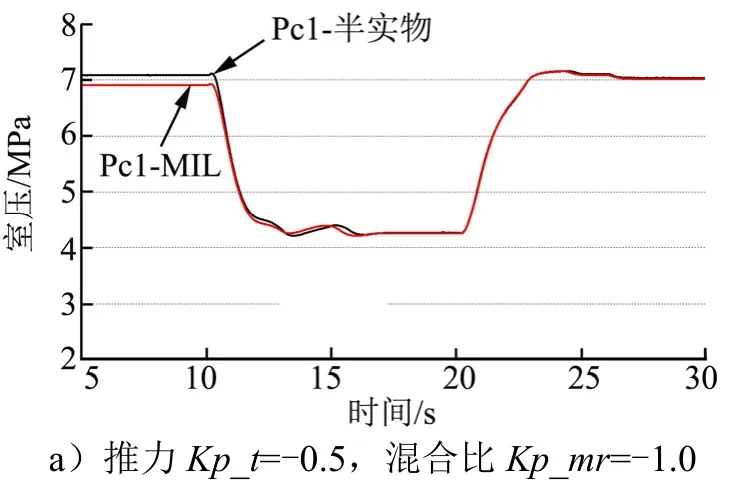
图8 推力调节过程室压MIL与HIL结果Fig.8 The MIL and HILResult of Chamber Pressure on Throttling Process
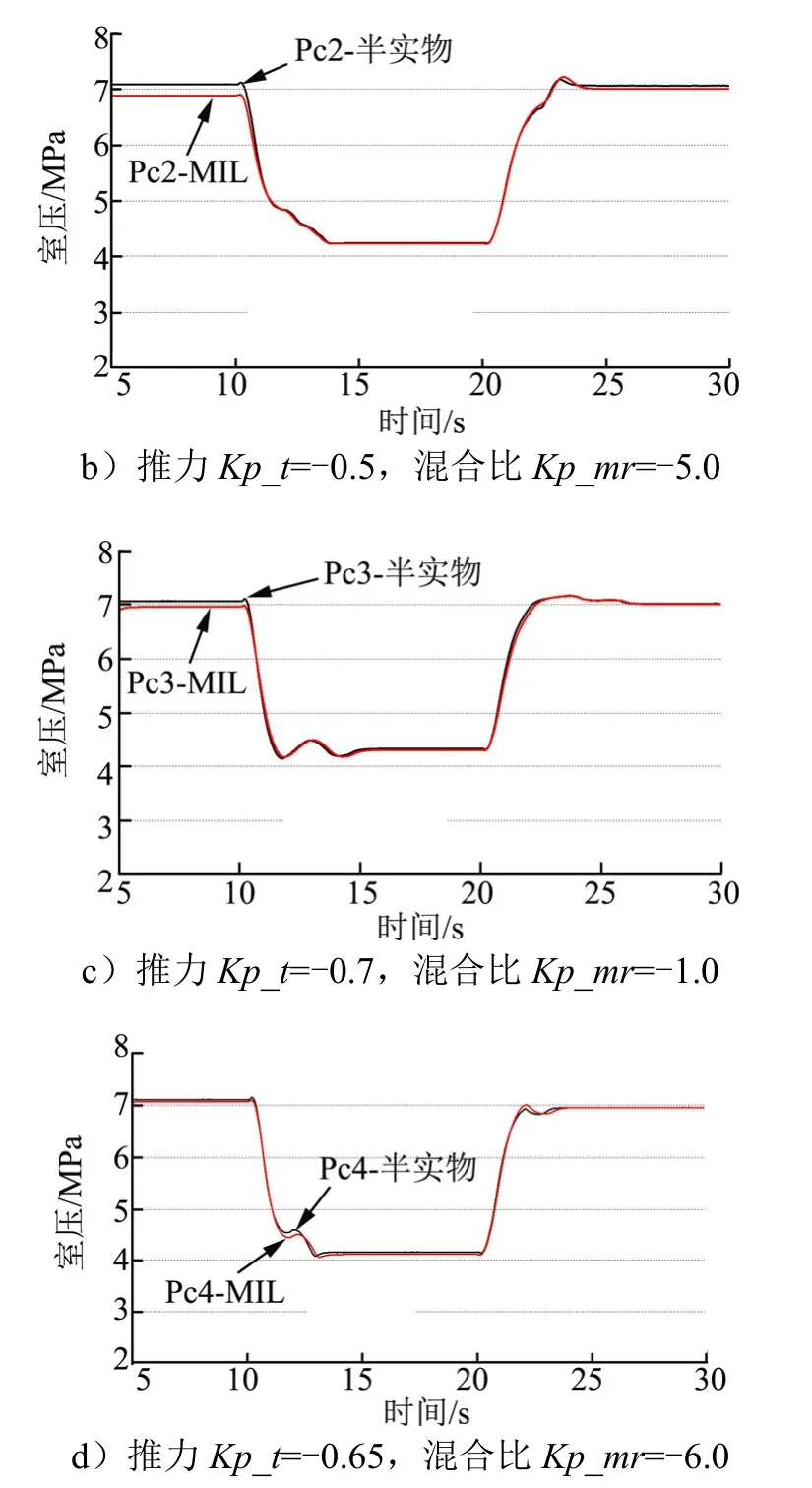
续图8
研究结果表明,推力调节过程中,HIL仿真与MIL仿真结果趋势及参数变化幅度较为一致,说明控制算法适应性良好。方案4的推力调节过程中,MIL和HIL仿真结果(图9)均显示,过程中混合比波动不超过11%,满足发动机组件工作需求,混合比稳态偏差不超过3.5%,满足控制算法设置的死区精度要求。
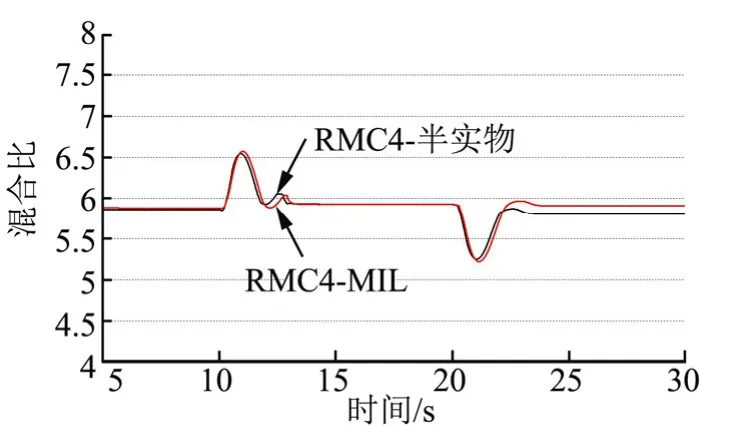
图9 推力调节过程混合比MIL与HIL仿真结果(推力Kp=-0.65,混合比Kp=-6.0)Fig.9 The MIL and HILResult of Mass Ratio on Throttling Process
HIL仿真仅有作动系统为真实系统,对比MIL和HIL的仿真结果可见,两种方法的研究结果相近,电机动态特性不是影响系统调节过程的主要因素。因此,未来可以通过MIL仿真来代替HIL仿真开展广泛而深入的控制算法研究。
本阶段完成了HIL仿真工作,充分验证了双控模式下两台电动调节阀工作协调性,电动调节阀均能够按照控制算法指令作动,实现发动机推力、混合比稳定控制。
5 结 论
针对某型氢氧膨胀循环发动机系统特征,提出了氢涡轮分流路和氧涡轮分流路分别设置推力调节阀和混合比调节阀、推力和混合比双PI闭环控制的方案。
通过模型在环仿真得到主要结论包括:a)推力负反馈、混合比正负反馈调节方案具有更好的调节效果;b)适当增大推力、混合比控制比例系数Kp_t、Kp_mr可有效改善调节过程系统动态响应;c)发动机调节过程对电机动态响应特性不敏感,允许机电时间常数略有增加。
通过硬件在环测试验证了电动调节系统模型的准确性,发动机能够实现60%~100%推力调节过程推力、混合比的联合控制,并将发动机参数平稳、迅速地调节至目标值附近。

