高温高压气井多封隔器管柱完整性分析方法及应用实例

刘洪涛 沈新普 刘 爽 沈国阳 秦世勇 沈国晓

1.中国石油塔里木油田公司 2. 中国石油大学（华东）

0 引言

封隔器是井下完井设备的主要部件之一，是用于致密油气储层改造压裂相关工程以及地层注水等施工措施的配套设施[1-5]。它的作用是将所在深度位置的油管—套管之间环空间隙封闭、隔离，保障具有较高压力的液体能按照预设的通道顺利进入地层。近年来，随着分段开采技术在常规和非常规油气资源开采中的普及，多封隔器的使用及相应的研究工作也越来越多[6-9]。

封隔器强度信封曲线的组成因素有两个，第一个是封隔器对轴向力的承载能力，第二个是对环空压差载荷的承载能力。一般封隔器生产商仅提供封隔器强度信封曲线，给出允许的载荷范围，不提供详细结构设计参数和计算原理。这样有时会导致按照强度曲线设计的封隔器管柱系统，发生意料之外的破坏[6]。中国石油塔里木油田公司迪西1井管柱系统中，使用了双液压封隔器，作为分段压裂的井下完井设施。在压裂施工过程中，双封隔器其中的一个封隔器发生芯轴断裂。为了分析芯轴破坏这个现象的机理，本文文献[10]采用三维有限元方法，分析了芯轴传压孔的应力集中现象。相关研究虽然部分解释了芯轴破坏现象的力学机理，但是由于缺乏对整个管柱的受力分析，所用的力学模型不完整。

单一液压封隔器的受力比较简单：其上受上部油管传递过来的轴向力作用，其下受下部油管传递过来的轴向力作用。下部油管的轴向受力一般为内外压力、浮力及重力。由于下部油管为自由端，它不受温度载荷的影响。在上下油管之间，封隔器受卡瓦等环空封隔零部件的压力和摩擦力。这些封隔零部件的摩擦力沿轴向分布，与咬合在套管表面的卡瓦一起，平衡了正常施工/生产工况下环空压差产生的载荷。但是在卡瓦咬合在套管表面之前，在短暂的坐封过程中，环空压差产生的载荷完全由封隔器芯轴及管柱来承担。

双液压封隔器管柱系统的受力比单一封隔器的受力分析要更加复杂：在温度载荷影响下，上部油管会受热膨胀，产生温度轴向力，下部油管由于不是自由段，也会产生温度载荷引起的轴向力。近10年来，有若干研究文献对多封隔器管柱力学进行了研究[10-15]。张智等[2-3]通过研究高压气井管柱多封隔器复合管柱力学模型，认为封隔器在井筒中的位置对管柱轴向力的影响较大。刘祥康等[1]针对水平井多封隔器高强度分段改造作业的情况，研究了井筒温压场对管柱力学行为的影响。沈新普等[10]分析了封隔器芯轴在水力压裂液体压力载荷作用下的弹塑性变形行为。胡志强等[8]研究了多封隔器在井筒封固段的密闭环空空间压力的温度效应。

本文提出了管柱力学全长分析+封隔器芯轴三维有限元分析的综合分析方法，用于分析计算多封隔器管柱的力学行为并评价封隔器的完整性，给出了相应的计算流程，并将之用于分析塔里木油田迪西1井芯轴破坏现象的分析，得到的变形及应力分布数值结果与观察到的现象能很好地匹配。实例说明了本文方法流程的有效性和实用性。

1 多封隔器管柱力学有限元分析流程

基于有限元数值方法的多封隔器管柱力学行为及封隔器完整性计算分析流程如图1所示。它包括两个部分：其中第一部分为管柱全长的有限元分析，第二部分为封隔器局部结构弹塑性应力分析。

图1 多封隔器管柱的力学行为与完整性计算分析流程图

2 多封隔器管柱力学有限元分析

2.1 迪西1井封隔器破坏问题描述

迪西1井采用了两个双封隔器进行分层压裂。两个双封隔器坐封位置分别位于井深4 612、4 850 m，两个封隔器的型号相同，均为MHR双筒液压封隔器，下部油管柱管柱结构如图2所示，全长4 942 m。压裂的目标储层位于4 808～4 830 m、 4 898～4 975 m。2012年9月17日在压裂施工过程中的压裂阶段观察到套压升高，判断油—套窜通。事后打捞出失效封隔器的零部件，发现两个封隔器中的下部封隔器完好、而上部封隔器的芯轴断裂，断裂位置位于芯轴上的传压孔附近。图3给出了断裂后的芯轴实物照片和结构设计图在断裂附近的局部视图。

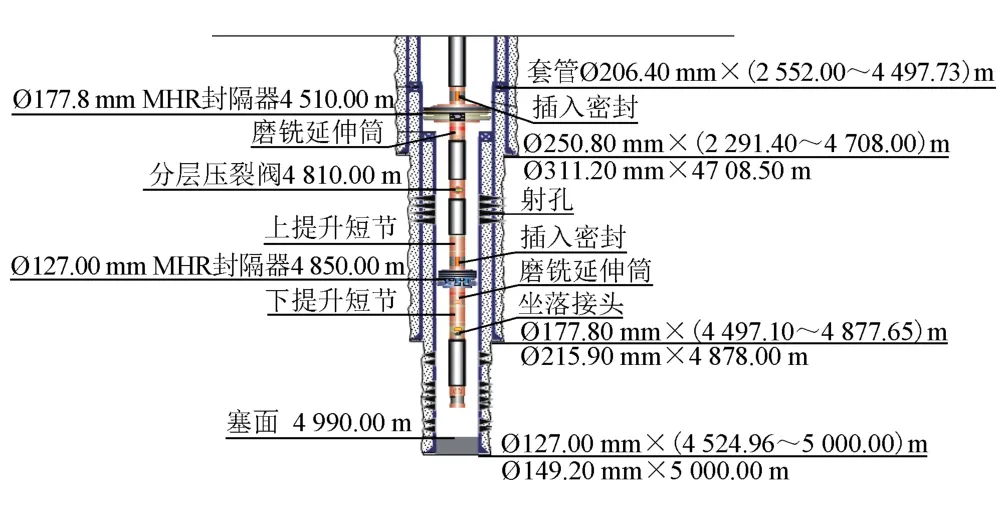
图2 迪西1井管柱结构图

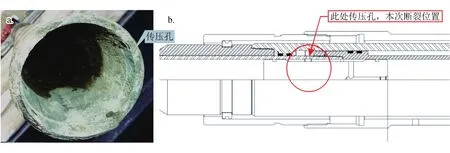
图3 断裂后的芯轴实物照片和设计图在断裂附近的局部视图

笔者从整体结构的管柱力学分析开始，采用三维有限元法分析管柱全长的应力分布，之后分析封隔器芯轴的局部构造中的应力分布与应变分布。下面将先介绍基本参数，然后介绍有限元模型，之后介绍有限元数值计算结果。这里先介绍整体管柱力学有限元模型及结果，之后再介绍封隔器芯轴的有限元模型及分析。

2.2 有限元模型及分析

2.2.1 管柱全长的有限元模型及参数

采用上一节的数据，建立了管柱三维有限元模型，并进行了数值计算分析。管柱力学三维有限元模型中，横截面上没有网格，只在轴向有网格划分。本模型采用1 647个三维一阶管单元pipe31H、1 648个节点模拟油管，1 667个管单元、1 668个结点模拟套管。这个管单元是专门用于模拟油管及套管的有限元模型。采用了1 647个ITT管—管接触单元模拟油管—套管的接触。有限元网格单元尺寸选取的基本原则是：由于采用的管单元是基于梁单元力学模式来进行计算的，单元的网格不是越密越好，一个单元的长度要大于截面直径的10倍，以保证单元的梁的力学属性。模型自顶端开始至油管底部设置了ITT接触单元。图4给出了管柱的4 942 m全长示意图，井口为坐标原点，这口井为直井。将管柱任一深度上的截面壁厚方向上分3层、环向1周共8个应力点，管柱截面上这些应力点1到24，共计24个应力点，如图4所示。双封隔器在坐封之后，双封隔器位移受到约束（图2）。为了表达简洁，本次计算选取了12个应力点进行应力校核和分析，应力点的编号为1～12。

图4 管柱截面应力点示意图

模型的载荷为自重载荷、内外压力、浮力、温度变化以及接触力。由于采用了MHR液压坐封的封隔器，管柱整体上可以不考虑坐封载荷的影响。但是在封隔器局部结构分析的时候要考虑液压的作用。

油管柱及封隔器芯轴材料参数取值分别如下，杨氏模量215 700 MPa，泊松比0.3，最小屈服强度758 MPa，抗拉强度862 MPa，热膨胀系数为1×10－5，钢材密度7 850 kg/m3。表1给出了油管柱和套管柱的几何尺寸、油套间隙以及截面积。

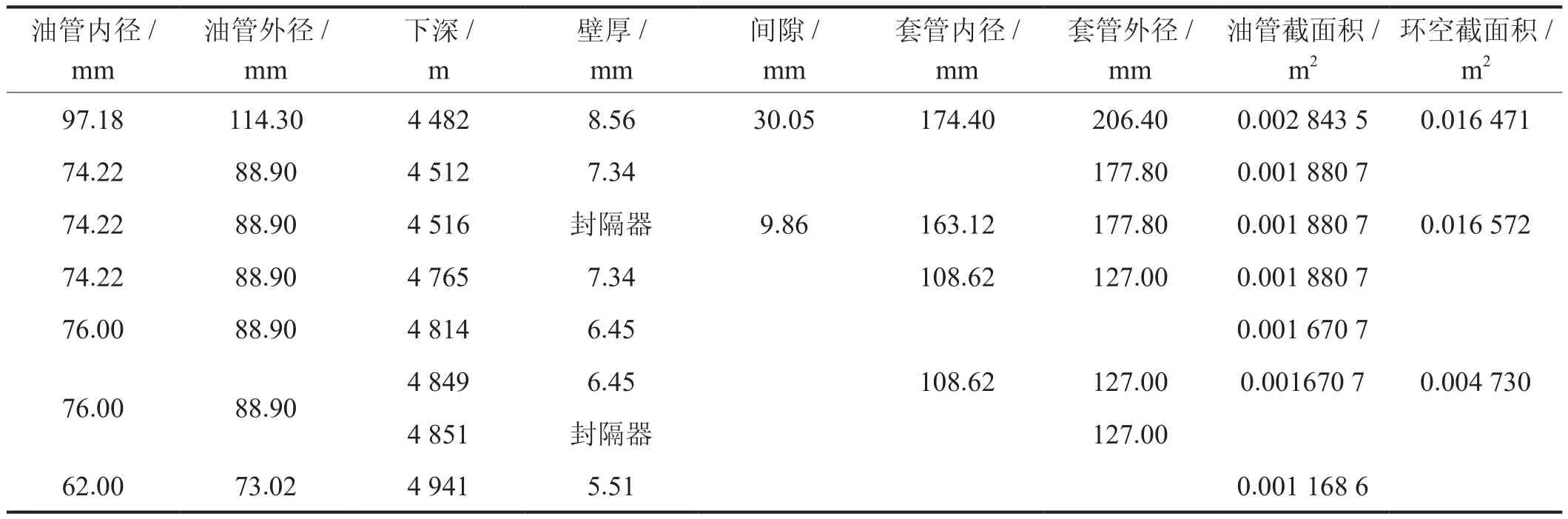
表1 油管柱和套管柱的几何尺寸表

封隔器坐封前环空保护液密度1.30 g/cm3，井口油、套压为0 MPa，井底油、套压为62.95 MPa。压裂施工注入流体密度1.03 g/cm3，施工排量4.3 m3/min，注入流体温度15 ℃，注入量260 m3，油管内油管摩阻8.36 MPa，油管柱载荷如表2所示。

表2 压裂时的载荷参数值表

由于两个封隔器把环空分成3个部分，相应地模型中需要对油管的环空压力分别赋值。

针对实际施工参数，开展酸压过程中的井筒温度场预测，预测得出酸压过程中双封隔器间井筒温度下降105 ℃（略去过程，简化模型的井下初始温度为130 ℃，压裂液进入后冷却，温度下降到25 ℃，温差载荷105 ℃）。

2.2.2 管柱全长的有限元数值计算结果

在重力、施工压力、浮力、接触力及温度变化引起的应力作用下，沿管柱全长的和轴向应力的分布由有限元数值计算得到，von Mises应力最大值为624 MPa，位于油管柱的井口位置，这个值明显低于管柱材料P110钢的屈服极限758 MPa。图5显示了在压裂施工时沿管柱下部的von Mises应力结果，横截面上内壁应力点3、9（这些点的位置参见图4）计算值。横截面上壁厚中间应力点选用2、6、10点计算值。横截面上外壁应力点12计算值。沿管柱壁厚方向各点的应力值有差异。在内外压、温度、重力及弯曲的共同作用下，大多时候内壁上的应力点von Mises应力值最大，外壁上应力点von Mises应力值最小。

图5 压裂施工下部管柱不同应力点 von Mises应力分布图

由图6可知，管柱截面上各点的轴向拉力相同。由于各点的轴向应力相同、曲线重叠，图6仅给出4个应力点的应力分布曲线（应力点10、6、2、12）。

图5和图6中，两个封隔器之间的轴向应力值与邻近区域的管柱段比较有明显升高。这是由于压裂液温度低、给油管柱造成降温收缩而产生的温度应力叠加其他因素造成的。两个封隔器坐封后，封隔器之间的管柱受约束不能移动，这使封隔器芯轴承受附加拉伸。而封隔器芯轴结构具有传压孔等细小构造，应力分布比较复杂。为了弄清芯轴的详细应力分布，必须建立芯轴的局部子模型[16-17]，进行三维有限元分析。根据图6的轴向应力分布图得知，在上部的封隔器的芯轴所受轴向力较大，其值为429 MPa。在结构上，封隔器芯轴位于封隔器上下两端的油管之间。通过螺纹连接，中空的芯轴与上下油管一起形成油气通道。

图6 压裂施工下部管柱横截面不同应力点轴向应力分布图

2.2.3 封隔器芯轴分析模型

图7为MHR双筒液压封隔器实物外形图及芯轴的有限元网格模型图。结合图3，断裂位置为封隔器第1组传压孔的位置。

芯轴所受的载荷包括两端的拉力、重力载荷、液压载荷以及来自卡瓦、橡胶块、液压筒等零件的力。这些作用力当中，两端管柱对封隔器芯轴施加的拉力是主要轴向载荷。卡瓦以及橡胶块等零件对芯轴施加的主要是径向压力。这些径向压力用以在套管上产生坐封所需的静摩擦力。它们产生的轴向力较小，这里可以忽略不计。

芯轴所受的液体压力，由于传压孔的连通关系，其内外表面上的液体压力大小相等，可以看作相互抵消。但是芯轴的凸起台阶处的液体压力能产生轴向载荷，必须计入载荷作用。

综合以上，本次计算中采用的芯轴模型的载荷简化为：①来自两端管柱的拉力；②芯轴台阶处的液体压力及传压孔上的液体压力。其他作用力被忽略不及。在计算管柱轴向拉力时已经计入了温度载荷。因此在计算轴向拉力作用下的封隔器的力学行为时不再重复计算温度应力。

图7 MHR双筒液压封隔器实物及芯轴的有限元网格模型图

由于芯轴的内外直径与管柱的内外径参数不一样，在施加轴向拉力载荷之前需要把整体管柱全长分析所得结果429 MPa的拉伸应力转换到芯轴截面上。表3给出了经过变换的芯轴等效截面应力354 MPa。芯轴的截面积比相连的管柱截面积要大。因此转换过来的轴向应力载荷要小一些。

表3 芯轴上的等效截面应力计算表

需要注意的一点是：在把管柱轴向力转化为封隔器芯轴轴向载荷时，由于管柱内外壁的轴向拉力/压力有可能不同，需要进行整个截面的平均化取值计算，然后才能确定相应的轴向拉力/压力载荷。当存在屈曲现象时引起的弯曲附加应力尤其需要关注。本文计算中的轴向力各点相同，如图7所示，没有这个问题。

2.2.4 封隔器芯轴数值计算结果

图8 封隔器芯轴在前述载荷作用下的塑性应变分布图

图8为封隔器芯轴在前述芯轴台阶处及传压孔上的液体压力及端部轴向拉力载荷作用下的塑性变形分布图。图9为von Mises应力分布图的数值结果。为了清晰展示结构内部的应力分布状况，取剖面展示等效塑性应变及von Mises应力的数值计算结果。由于载荷已经超过了结构的强度极限承载能力，液体压力及轴向拉力载荷加载到73%的载荷量时就达到了塑性屈服极限，以力载荷为加载形式的计算不再收敛。这和实际工程中观测到的芯轴断裂现象十分吻合。

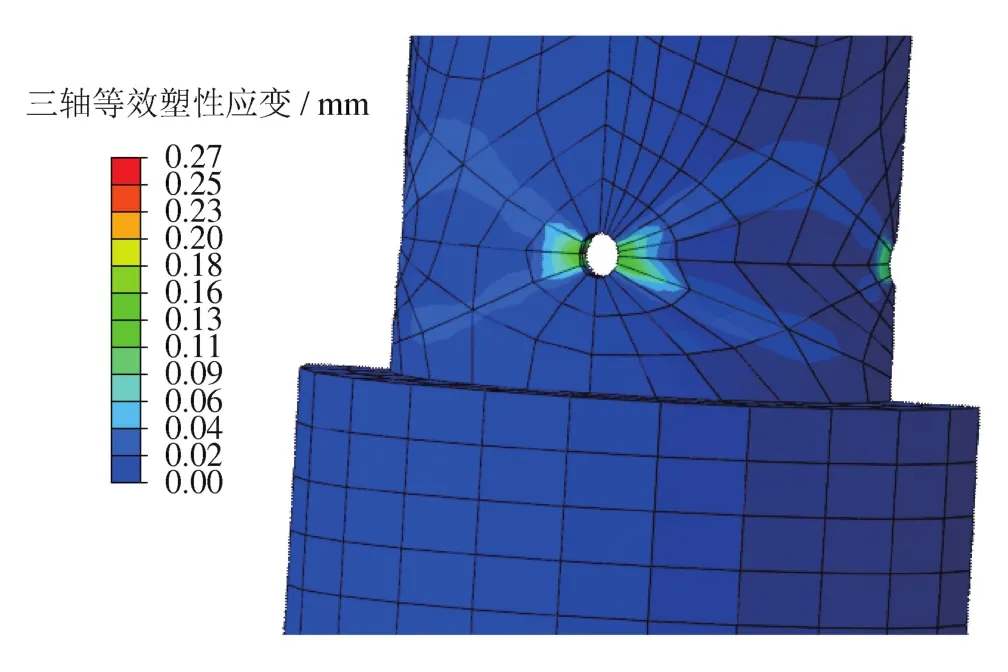
图9 封隔器芯轴外表面上的分布图

从图8看出，当载荷达到73%的总量时，等效塑性应变的最大值达到0.278 1，即27.81%，这属于明显塑性变形。图8还显示出了芯轴结构在第一组传压孔附近的塑性变形区连成了一片，导致结构达到了塑性极限，不能继续承受更多的载荷。通过图8右面的局部放大图看出：塑性变形仅在第1组传压孔处。第2组传压孔附近基本没有塑性变形区。

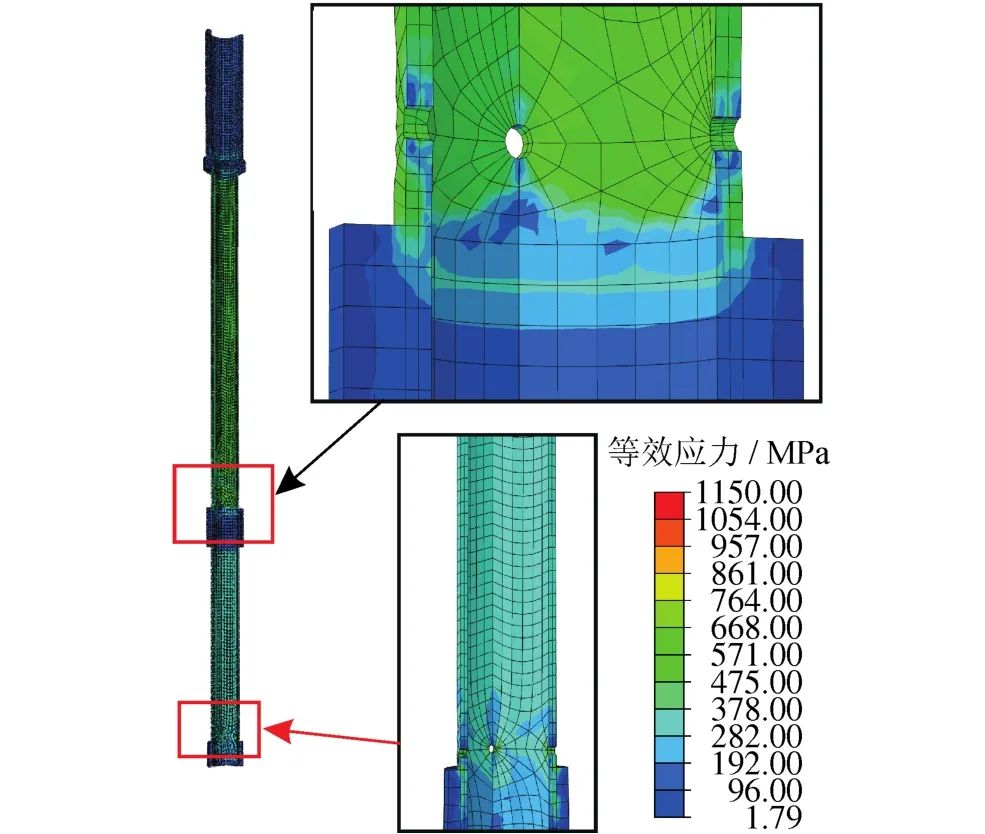
图10 芯轴的von Mises应力分布图的数值结果图

图9为封隔器芯轴在前述载荷作用下塑性变形在芯轴外表面上的分布图。从图10看出，塑性区出现局部化趋势，沿着最大剪应力的方向形成了一条塑性剪切带。图10给出了芯轴结构中的von Mises应力的分布情况。从图10看出，结构中的应力峰值远远超过材料的初始屈服极限757 MPa，满足了塑性变形加载条件。

3 结论

1）提出了一个用于双封隔器管柱系统力学行为分析的三维有限元计算流程。结合塔里木油田迪西1井封隔器芯轴在压裂施工载荷作用下破坏的实例，展示了这个流程的有效性和实用性。

2）计算首先对整体管柱全长进行了三维有限元分析，求得了在压裂施工的载荷工况下管柱各处的应力分布，包括轴向应力和von Mises应力。数值结果显示：在重力、液体压力、和温度应力的作用下，下部封隔器以上至井口管柱各处的轴向应力状态为拉应力。在两个封隔器之间，由于温度应力的影响，拉应力较常温情况明显增大，应力表现异常，但是等效应力峰值为629 MPa，仍然在初始屈服强度758 MPa以下，仍属于弹性应力范围。

3）通过对封隔器局部结构建立有限元模型，采用三维实体单元对芯轴进行弹塑性分析。数值结果表明: 在管柱轴向应力和液体压力共同作用下的芯轴发生了明显的塑性变形。在总载荷73%的载荷量作用能够下，芯轴在传压孔附近发生明显的塑性变形区。且随着载荷增加，塑性变形区连成一片，使结构达到塑性极限而不能继续承受载荷增加。塑性变形发生的位置位于第一组传压孔附近。第二组传压孔附近没有塑性变形区。

4）为了避免以后出现此类封隔器芯轴断裂，在两个封隔器之间，应该设立伸缩节，以缓解温度下降导致的封隔器芯轴所受轴向拉应力过大的现象。另外，采用更高强度等级材料的芯轴，能承受更高的施工压力及温度载荷，也是降低芯轴断裂风险的有效方法。