基于SLM的多内腔结构件自适应分层算法优化

孙玉龙

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

20世纪80年代，3D打印(three dimensional printing)首次被提出，被称为“第三次工业革命的重要工具”[1]。1995年，德国首次提出选区激光熔化成型(selective laser melting，SLM)技术[2]。SLM采用3D打印原理，层叠成型，可设计性好，成形连续，有较好的表面质量和物理性能。因此该技术适合成形具有复杂形状的金属结构件。

目前针对复杂内腔结构的相控阵雷达天线，国内常采用传统机加工进行制造并焊接装配。该方式存在着加工时间长、成品率不高、电性能不足等缺陷。因此本文基于SLM技术，通过对传统分层算法的优化，提出新的自适应分层算法。

目前分层算法研究主要包括两方面：等厚分层和不等厚分层。国内外众多学者对此进行了相关研究。JAMIESON R等[3]规范了等厚分层方法，即直接分层算法(DS)。直接分层是3D打印中最基础的分层方法，其核心参数是分层厚度。当层厚值确定后，所有分层得到的二维轮廓线信息也随之确定。等厚分层方法虽然比较简单，但在STL模型轮廓曲率变化较大处，如果分层厚度过大，会产生明显的阶梯效应[4]。DOLENC A等[5]针对成形过程中出现的阶梯效应，提出了一种自适应分层方法。该方法通过定义分层切片与三角面片交点处的允许切削深度值，来确定分层层厚；虽然该算法能够有效抑制台阶效应带来的表面质量降低问题，但没有针对性，对于内腔结构较少甚至均为实体的区域，会大大降低分层及加工效率。TYBERG等提出了一种针对模型局部特征进行自适应分层的方法。该算法能够有效成形局部特征，但由于SLM成形刮粉时得到的粉层厚度是一致的，因此若要加工的内外层厚不同，对设备的要求非常高，甚至无法有效实现。CORMIER等人基于非统一的切削深度值对成形表面的影响，提出了一种算法，可以允许用户根据零件表面质量需求，定义不同层面的最大切削深度，满足不同区域的分层要求。印度理工学院的CHAKRABORTY D等[6]提出的算法可以直接输出基于表面与平面相交算法的分层文件等。文献[7]提出相邻分层的面积偏差比值来自动调整分层厚度，由于基准面积是不断变换的，很难控制，导致计算的分层厚度不准确。文献[8]提出了在“阶梯效应”中建立体积误差模型，通过控制参数实现自适应分层。但当分层厚度超过某些三角面片时，会导致特征遗失或体积偏差较大，因此很难得到准确的分层厚度。

上述分层算法的原理研究已趋于成熟，并形成了种类繁多的分层算法。但是目前较为成熟的算法，对多内腔结构零件成形时的分层问题依然不能很好地处理，因此本文在相对面积偏差比值的分层算法上提出了优化算法，以满足成形分层要求。

1 特征结构的自适应分层算法

本文以毫米波雷达为对象，其结构剖面如图1所示。该研究对象内部包含了多种不同尺寸的内腔结构。本节将基于相对面积偏差比值的自适应分层算法进行优化。

图1 多缝隙内腔结构天线剖面示意图

1.1 相对面积偏差比值分层算法

相对面积偏差比值定义为：

其中Ai和Ai+1是分层中相邻两个切片的面积。这里参数ε0由需要的表面精度值来确定，一般选择该值为ε0=5%。

每层轮廓有内、外环等多环的情况，因此第i层面积为：

对于沿打印方向有曲率变化的零件，总能找到一个厚度值，使截取的轮廓面积差值在某个范围内。基于该原理，可以先采用最大层厚进行切分，然后判断ε是否小于指定值。若ε超过标准值，则表明当前模型表面特征有较为明显的变化，此时按照一定的规则，使用较小的分层厚度继续进行细分直到满足条件。

基于相对面积偏差比值的自适应算法判别条件简单，易实现。但在某些特殊情况下，其分层的自适应效果并不理想，例如相邻两层轮廓面积差为0的情况。

如图2所示，为毫米波天线轴向的局部剖面图。在该方向可分为7个特征区域，每个区域都由多个内腔组成。

图2 毫米波天线局部剖面图

在这7个区域交接处，切片轮廓面积会发生突变，因此采用面积偏差比值的自适应算法会有很好的分层效果。但在同一区域内，切片轮廓面积差为0，因此采用最大层厚进行切分，会使成形的内腔特征精度不足。

1.2 自适应分层算法优化

上述算法不足之处在于无法有效识别面积偏差比值为0的多内腔结构。通过对大量内腔体结构件的对比分析，发现该类结构的横截面有以下几个特征：

1) 所有截面内环面积之和占外轮廓面积的比值较高；

2) 截面内环的总数量较多。

若不能同时满足以上特征，则不能判断为多内腔结构。如图3所示。

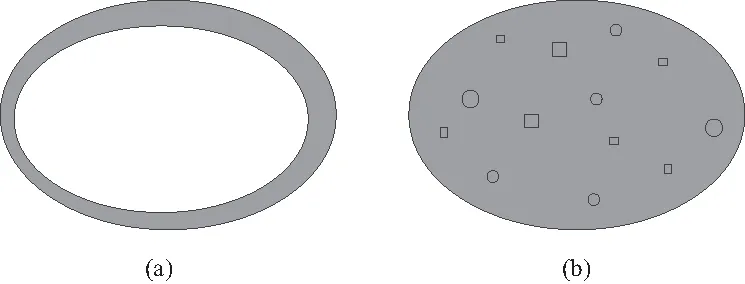
图3 非多内腔结构示意图

在图3(a)中，内腔轮廓总面积很大，但只有一个；图3(b)中，虽然内腔数量较多，但其总面积较小，属于微小孔洞成形。张冬云等人[9]针对薄壁和微孔结构成形过程的工艺进行了研究，因此该情况不在本文讨论范围内。

定义第i层切片内轮廓总面积相对外轮廓总面积的比值σ，即内轮廓面积占比为：

σ0为常量，由用户根据待加工对象的结构特征要求进行定义：若对象内腔数量多、面积大，可以将σ0的数值设置在较高水平，反之较低。

当内轮廓面积占比为定值时，内轮廓数量越多，每个内轮廓面积与外轮廓面积的比值会降低。定义内轮廓面积平均占比μ为：

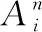
对于多内腔结构，在满足σ≥σ0的情况下，内轮廓面积平均占比μ的值在一定范围内波动，即：μ0≤μ≤μ1。经过计算，在极端情况下，μ0的取值为0.002 5。考虑到孔洞分布不均，外轮廓尺寸变化等因素，给出的判别下限取值余量μ0=0.005。μ1范围上限则由用户根据成形需求进行设置。

为了统一两个判别条件，定义判别系数θ：

其判别效果为：若当前层内轮廓面积占比满足条件，则θ=1，不影响后续内轮廓面积平均占比的计算；若当前层内轮廓面积占比不满足条件，则取值为虚数，直接采用既定的分层算法对当前层进行切分。

综上判别条件可以表示为：

因此，根据基于相对面积偏差比值的自适应分层算法的优化思想，设计出优化算法的代码流程如下：

1) 用户定义可允许的面积偏差比值ε，最小层厚lmin，最大层厚lmax，内轮廓面积占比σ0及内轮廓面积平均占比μ1；

2) 读取STL文件，并对模型数据进行预处理；

3) 获取所有面片顶点中z坐标值的最大和最小值(zmax和zmin)，并用Zslice=zmin水平面切分模型得到的首个轮廓线并存储；

6) 计算ε，判断ε≤ε0，成立跳至步骤9)，不成立跳至步骤7)；

7) 令Zstep=Zstep-lmin，判断Zstep

9) 计算当前层判别系数θ，并计算内轮廓面积平均占比μ。若μ0≤μ≤μ1成立，则Zstep=lmin；若μ0≤μ≤μ1不成立，则Zstep=lmax，之后跳至步骤10)；

11) 结束。

2 算法实现及实验验证

本文基于MFC开发平台，利用面向对象编程技术及OpenGL图形库对模型文件进行读取与显示。由于研究对象原始尺寸较大(φ256mm×16.4mm)，而内部腔体结构呈中心对称分布，因此为了研究方便，仅截取中心φ20mm部分进行数据处理。为了对比研究，算法采用了等厚分层、相对面积偏差比值的自适应分层以及优化后的分层方式。

为了更清晰直观地描述分层效果，这里设置最大分层厚度lmax=0.1mm，远大于实际加工中最大层厚度50μm的尺寸，而最小分层厚度lmin=0.03mm，同时设置每5层的显示效果。

如图4所示，图4(a)为截取的天线局部模型；图4(b)为等层厚分层效果，共得到165层切片信息，包括在区域分界处的11层切片信息。图4(c)为采用相对面积偏差比值的自适应分层算法，共得到179层切片信息；图4(d)为采用优化后的自适应分层的分层结果，共得到264层切片信息。

从切片结果可以明显看出，相对面积偏差比值分层结果与等层厚分层结果效果类似，只有在区域分界处该算法对分层进行了细化，除此之外的区域(包括零件上半部分的多内腔结构)都采用最大层厚的均匀分层方式进行切分。而优化的分层结果则表明，对特征结构进行了有效细分。因此设计对比试验中，为了更好地判断优化分层的加工效果，采用几组等层厚分层与优化算法进行对比。

图4 3种分层算法的结果比较

为了对比本文优化算法下的加工精度可以达到的水平，设置等厚分层下的加工试验作为对比：

1) 等层厚分层成形方案：首先以设备的加工参数库中最优加工层厚l=30μm为参考基准，并以该基准为标准，上下各设置两组层厚，分别为20μm、25μm、30μm、35μm和40μm，共对5组不同厚度分层进行试验。

2) 优化算法分层成形方案：经过对本研究对象内腔结构的计算，取各参数σ0=0.45，μ0=0.005，μ1=0.167，取最大层厚lmax=40μm ，最小层厚lmin=20μm，对模型进行切片，导出SLC格式文件至打印设备进行打印。

成形后采用线切割将样件剖开，取内腔表面5处不同的点进行表面粗糙度测量，并取平均值作为该组试验的表面粗糙度。

为了保持试验条件的一致性，对于内部轮廓填充，两组试验均采用相同的扫描参数：激光功率140W、扫描速度800mm/s、扫描线间距为0.085mm、层间扫描角度偏移量为90°。

在加工前，需要确定不同层厚下成形过程中的激光热影响区，因此对本文设计的5种层厚分别做单道成形试验，结果如图5所示。图5(a)-图5(e)分别为层厚20μm、25μm、30μm、35μm与40μm下的单道成形试验。本文所用设备的光斑半径实测值为70μm。通过对5种成形参数的单熔道尺寸测量，可以得到实际的熔道宽度分别为112μm、116μm、118μm、121μm及126μm，因此本文涉及的试验热影响区宽度分别为：21μm、23μm、24μm、25.5μm及28μm，以此来设置相应的补偿值。

图5 不同层厚的单道热影响区试验结果

试验结果如表1与表2所示。由表1可以看出，等厚分层成形下，最小层厚20μm与最大层厚40μm的成形表面精度差距较大，表面粗糙度值相差约3.5μm。虽然最小层厚20μm下的成形质量较好，但是分层总数明显较多，约为最大层厚的2倍，而成形时间增加1个多小时。

表1 等厚分层成形试验结果

表2 优化的自适应分层成形实验结果

而在表2中，由于采用优化的自适应分层算法成形，其成形质量与等厚分层中最小层厚的加工精度相当，但其加工时间与分层数量约处于等厚分层30μm左右的水平。由于本试验对象仅为天线局部，若对天线整机进行成形，则对于该试验中不同情况的加工时间差距会非常大。从上述试验数据可以得知，采用本文优化的自适应分层算法，能够在保证成形精度的前提下，减少分层厚度，提高加工效率。最终成形局部零件与表面形貌如图6所示。图6(a)为成形样件；图6(b)为线切割样件；图6(c)为放大500倍后的内腔微观形貌图，可以看出其表面除了迸溅点外，其余部分光顺，无凹凸点。

图6 成形件及表面形貌图

3 结语

本文主要基于SLM成形技术，针对具有多内腔结构件的自适应分层算法进行了分析研究。通过研究发现，本文提出的优化算法能够在保证加工精度满足要求的情况下，尽可能减少分层所用时间，提高加工效率。