切削机器人任务空间的动力学优化

夏恩帅，张永贵，刘永平，牛 蓉

(兰州理工大学机电工程学院，甘肃 兰州 730050)

近年来，六自由度机器人由于其具有操作的机动性和灵活性，以及能够代替人类从事一些单调、繁重的工作，越来越受到各方的重视[1]。

六自由度切削机器人动力学建模，采用牛顿-欧拉法可以得到效率很高的模型递归方程，非常适合数值计算，计算复杂程度也相对较低[2]。本文以六自由度串联切削机器人为研究对象，首先运用SolidWorks软件建立其三维模型，获得切削机器人的动力学参数；然后以牛顿-欧拉法为理论方法建立切削机器人的动力学方程，同时分析切削机器人的工作空间，确定任务空间和机器人基坐标系的相对位置[3]；最后通过遗传算法得到切削机器人的最佳位姿。本文的研究成果可为六自由度串联切削机器人的动力学研究奠定理论基础。

1 运动学模型的建立

运用SolidWorks软件建立的六自由度串联切削机器人三维模型如图1所示。

对图1所示的切削机器人，采用后置D-H法建立其连杆坐标系[4]，如图2所示，切削机器人的D-H参数见表1。

图1 六自由度串联机器人三维模型

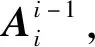
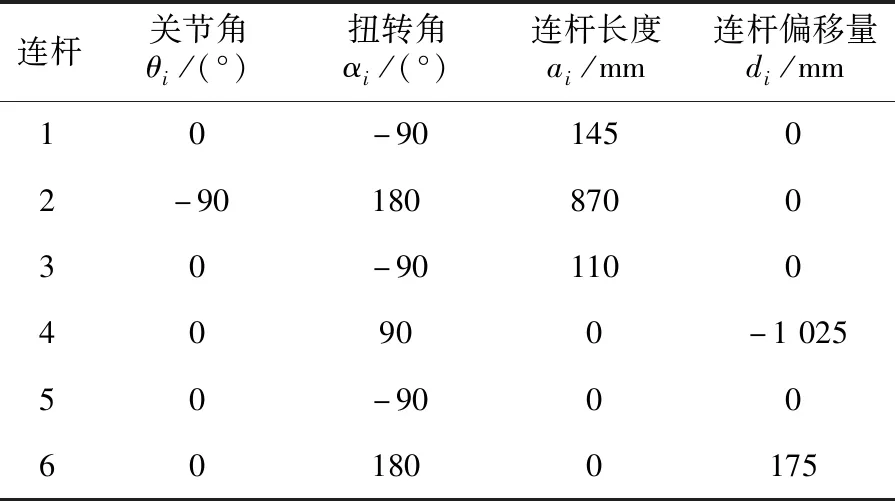
表1 六自由度串联切削机器人的D-H参数

(1)

(2)

通过MATLAB中机器人工具箱的link等函数，计算θ1,θ2,θ3,θ4,θ5,θ6均为0时末端执行器在机座坐标系中的位姿，从而得到式(3)，机器人的MATLAB模型如图3所示。

图3 机器人MATLAB三维仿真模型

(3)

2 动力学模型的建立

为更好地了解机器人运动过程中各关节的速度、加速度和关节力矩等参数，通过建立机器人动力学模型来分析研究机器人的动力学特征[5]。本文运用牛顿-欧拉法建立六自由度串联切削机器人的动力学模型，其力平衡方程(Newton方程)和力矩平衡方程(Euler方程)如式(4)所示：

(4)

式中：fci为作用在杆件i上的外力合矢量；nci为作用在杆件i上的外力矩合矢量；mi,vci,aci,ωi,εi分别为杆件i质心的质量、线速度、线加速度矢量、角速度和角加速度；Ici为杆件的惯性张量；t为时间。对于杆件i则有以下的公式：

(5)

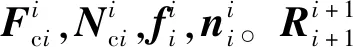
(6)

(7)

3 机器人工作空间与任务空间分析

3.1 确定机器人工作空间

六自由度切削机器人的工作空间如图4所示，图4是根据六自由度切削机器人的相关参数通过MATLAB仿真得到的，图中的点为机器人末端执行器驻留过的痕迹点，总点数N=30 000。切削机器人各个关节的转角范围是：θ1=[-180°,180°],θ2=[-90°，135°],θ3=[-160°,280°],θ4=[-360°，360°],θ5=[-125°，125°],θ6=[-360°，360]。

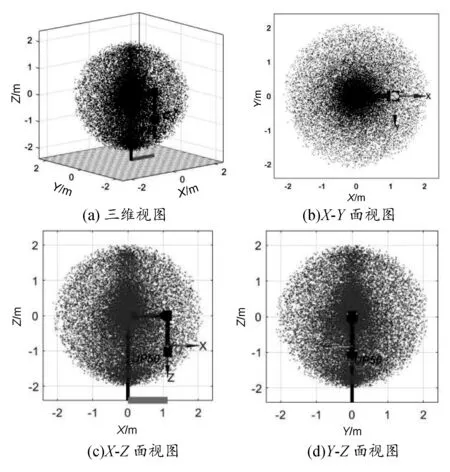
图4 机器人工作空间

根据六自由度串联切削机器人的各杆件参数和MATLAB仿真模拟得到的机器人工作空间示意图可以知道，机器人工作空间上下边界之间的最大距离为3 547 mm，左右边界之间的最大距离为3 802 mm。

3.2 任务空间的描述

对于切削机器人来讲，铣刀安装在机器人执行器末端。根据切削机器人切削加工时的工艺要求，铣刀工作的空间为一个二维平面，因此切削加工时铣刀垂直于工件表面，并保持此姿态按照给定的运动规律来完成对工件表面的切削[6]。本文以一个长1.0 m、宽1.0 m、高0.3 m的长方体的表面作为被切削工件表面为例，机器人任务空间如图5所示，机器人机座坐标系为Σ0，工件坐标系为ΣW，机器人末端铣刀的附体坐标系为ΣQ，上述几个坐标系的变换关系如式(8)所示：

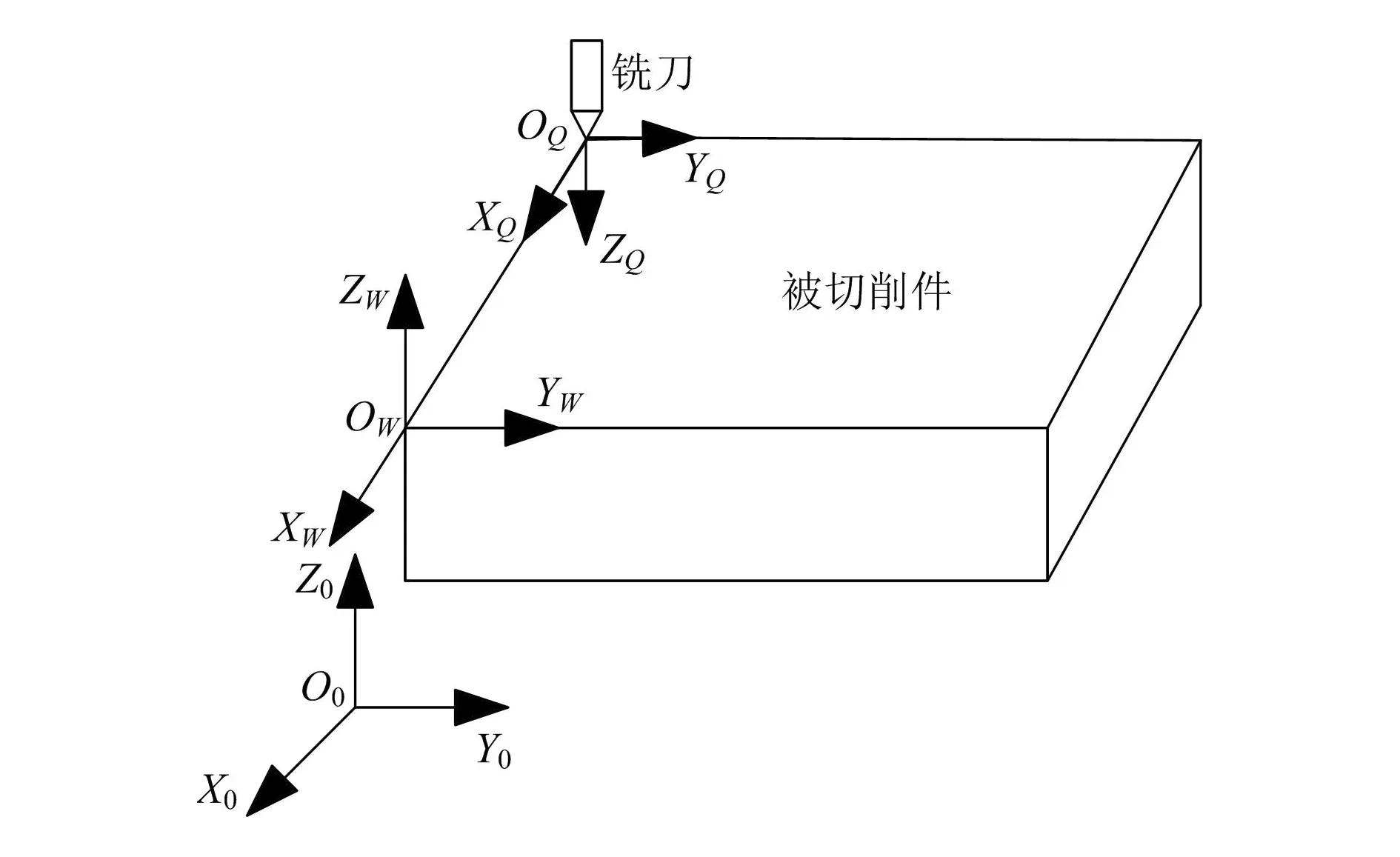
图5 切削任务示意图

(8)

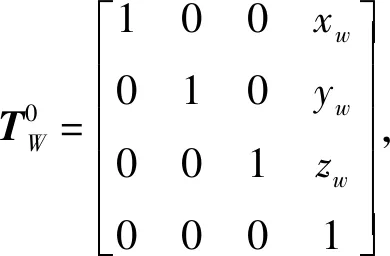
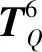
根据式(8)可以将该任务空间转换到在机器人的机座坐标系中，并可求解各任务点对应的关节位置。其任务空间表达式为：

(9)

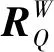
3.3 任务空间在工作空间中的描述

图6为工作空间与任务空间的X-Y面和X-Z面轮廓，图6(a)中的实心方块为被切削工件的X-Y面，图6(b)中的实心图形为被切削工件的X-Z面，取(xw,yw,zw)=(0.5，-0.5,-0.2)。由图6可知，任务空间完全在工作空间内，被切削件的加工表面全部处于六自由度切削机器人的工作空间内。

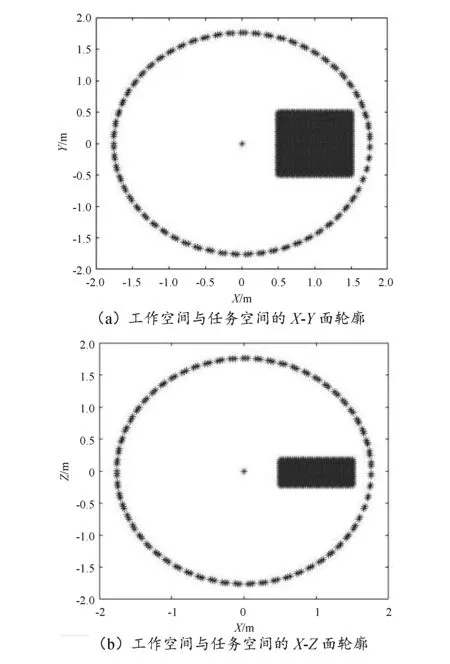
图6 机器人工作空间与任务空间

4 基于动力学的任务空间位姿优化

切削机器人在其工作空间内进行切削加工时，切削加工任务空间在机器人工作空间处于什么样的位姿，会影响到机器人的工作状态[7]。只有机器人自己先达到一个“舒服”的姿态，才可以更好地去完成任务。这个“舒服”的姿态指的就是机器人末端铣刀在任务空间工作时在达到所要求的位姿、速度、加速度的同时，机器人每个关节的驱动力矩τi的和∑|τi|(i=1，2，…，6)为最小。

图7为切削机器人末端铣刀在工件表面工作的示意图。被切削工件表面为边长1 m的正方形，本文选用的铣刀外径D=8 mm，在AD边、BC边各取100个点(图7中a1,d1,a2,…；b1,c1,b2,…)，每两点之间相距10 mm，a1点距AB边4 mm。以铣刀将要接触而未实际碰触工件表面时的位置点为起始点，以铣刀完全离开工件表面时的位置点为终止点，以此过程为一个单次的走刀轨迹(如a1—b1)，之后铣刀从b1横移到c1，进行下一次走刀(c1—d1)，如此往复，按a1—b1—c1—d1—a2—b2…的轨迹顺序走刀，直到铣刀从d50点完全离开，结束整个工件表面的铣削加工。

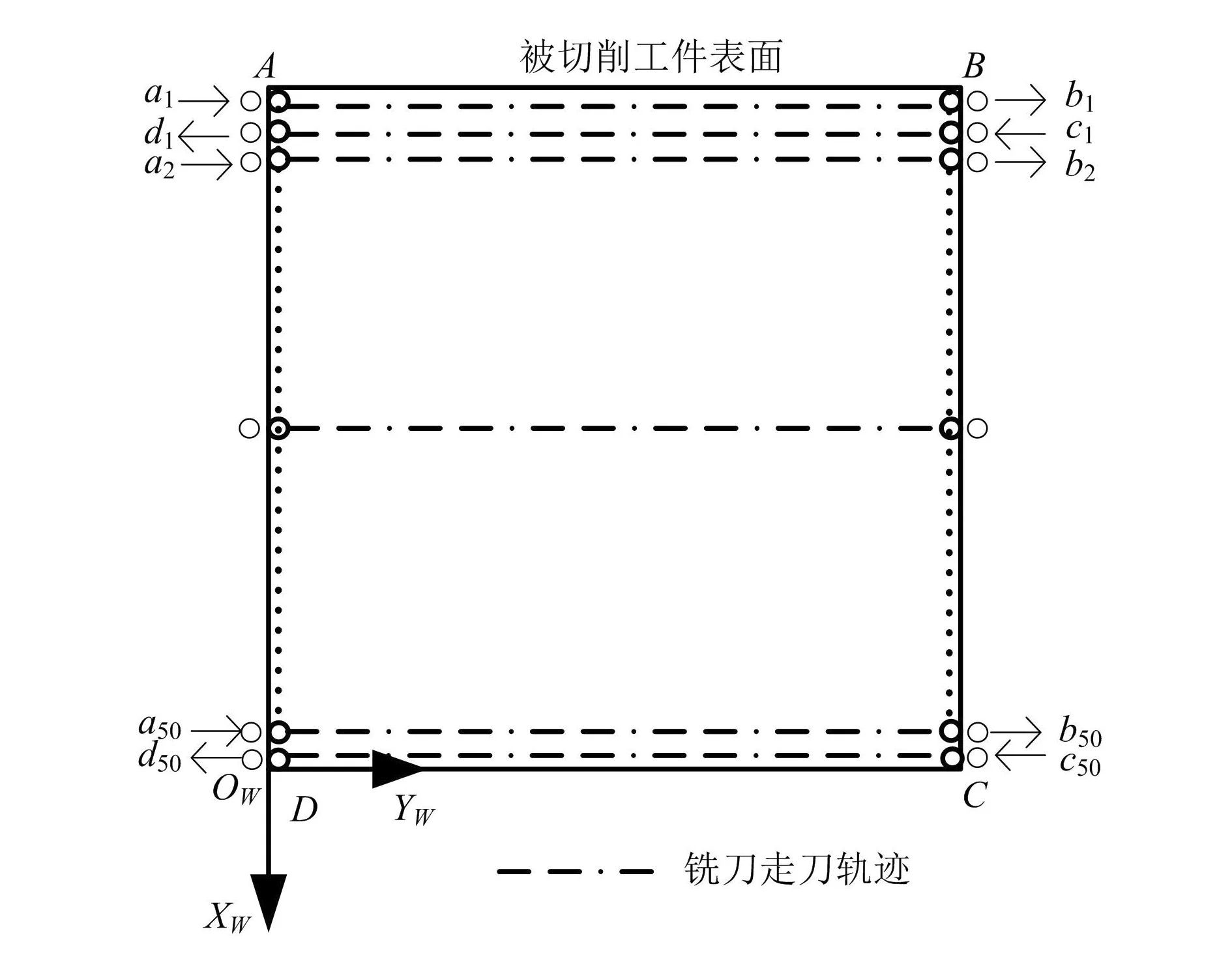
图7 切削加工示意图

在铣削时，温度、刀具材料、铣削液、齿轮进给量、铣削力系数等都影响着铣刀工作时的铣削力。本文铣刀采用高速钢，工件材料为灰铸铁，铣削力系数Cp=30，铣刀外径D=8 mm，铣削深度为t1=6 mm，每齿进给量Sz=0.4 mm/齿，铣刀齿数Z=4，铣刀宽度B=8 mm，铣削力F的计算公式为：

(10)

式中：PZ为铣削力，也是切向力。

由式(10)可以计算得到铣削力F=3 251 N，铣削时采用顺铣。

4.1 优化算法的描述与应用

一般pc取0.25～1.00，本文取0.80，变异概率pm=0.05，运用两人竞赛选择法，每次随机选择得到两个个体，从这两个个体里选出适应度值小的个体作为新种群的个体，一直到新种群被填满为止。为了防止其结果出现收敛于局部最优点的情况，每隔10代对种群重新进行一次初始化，然后将前一代的最优个体放到新的种群中，如果有更优个体出现，则前一个自然会被淘汰[11]。同时为保证最优个体在选择的过程中不被遗漏，采用精英模型将最优个体保存。

在交叉和变异的过程中，利用交叉算子和变异算子对父代种群Pk0进行作用，并通过与给定的交叉概率pc和变异概率pm比较来判定是选择交叉还是选择变异，若随机数<0.8，则对父代进行交叉操作，若小于pm，则进行变异操作。在执行交叉操作过程中使用算数交叉，选择某一个体i,并用另一个选出的个体u与之交叉，交叉算子如式(11)和(12)所示：

pk+1(u,j)=pk0(u,j)ruj+pk0(i,j)(1-ruj)

(11)

pk+1(i,j)=pk0(i,j)rij+pk0(u,j)(1-rij)

(12)

式中：pk+1(i,j)为群体中第i个个体的第j位变量；pk0(·)为第k代群体中选择出的要继续繁殖的个体组成的父代；rij,ruj为随机数。

对每一个体i的每一位取一个随机数，当随机数<0.05时，采用非均匀变异对该位进行变异操作，使用的变异算子pk(i,j)如下：

(13)

或

pk(i,j)=[Tb(j)-pk0(i,j)]×rx×(1-

(14)

式中：Tb(j)和Lb(j)为个体i第j位的上、下边界；k和kmax分别为当前代数和最大进化代数；随机数rx决定了变异算子是采用式(13)还是式(14)，其取值范围为0～1，当rx大于0.5时，采用式(13)，否则采用式(14)，对每一个需要变异的个体，rx都要重新选取。

为保证被切削件整体处于机器人切削工作空间内，各个变量的取值区间分别为：xw∈[-1，1]，yw∈[-1，-0.5]，zw∈[-1，0]。经过300代的优化计算，得到优化结果为：xw=0.521 5 m，yw=-0.468 9 m，zw=-0.256 8 m。需要指出的是，这个优化结果中的(xw，yw，zw)是工件坐标系相对于机器人机座坐标系进行平移后最优的一个位姿矢量。为了工件安装的方便，工件加工面与机器人基坐标系X-Y面相平行。

4.2 优化算法的调试与验证

采用上述遗传算法进行任务空间位姿优化时，为防止切削机器人末端执行器在某一位置时虽所有关节力矩和最小，但其中某一个关节力矩超过允许力矩的情况发生，采取如下措施：当前代最优个体的函数值的绝对值大于设定值K时，停止对遗传种群的选择操作、交叉操作和变异操作，此时以本代最优个体Xa(j)为中心按随机数r进行随机搜索，用算子p(i,j)重新初始化(initialize)种群：

(15)

此时以|f1,Xa|/n为搜索步长，计算每个个体的适应度函数值f1，从而得到满足条件的最优个体。对每一个体取随机数r，当r≥0.5时，式(15)取加号“+”，否则取减号“-”。当f1大于等于设定值K时，整个过程结束。

当任务空间的坐标系原点分别处于(x,y,z)=(0.5，-0.5,-0.2)点和(xw,yw,zw)=(0.521 5，-0.468 9，-0.256 8)点时，以切削机器人的末端执行器从初始位置到距离切削机器人基坐标系最远端的b1点为一铣削过程，对比两个过程中机器人各关节的力矩变化，如图8所示。

六自由度切削机器人关节1,2,3的允许力矩分别为196 N·m、196 N·m和127 N·m，图8中Torque01为任务空间基坐标系原点在(x,y,z)=(0.5，-0.5,-0.2)点时的力矩变化曲线，Torque02为任务空间基坐标系原点在(xw,yw,zw)=(0.521 5，-0.468 9，-0.256 8)点时的力矩变化曲线。由于篇幅有限且其余关节力矩较小，因此其余关节力矩变化曲线不再一一给出。由图8中Torque01变化曲线可知，关节1,2,3的最大力矩分别为17.551 4 N·m、113.872 9 N·m、11.027 0 N·m；由Torque02变化曲线可知，关节1,2,3的最大力矩分别为8.733 4 N·m、79.496 3 N·m、10.152 8 N·m。由此可以知道关节1,2,3的最大力矩都未超出其允许力矩。

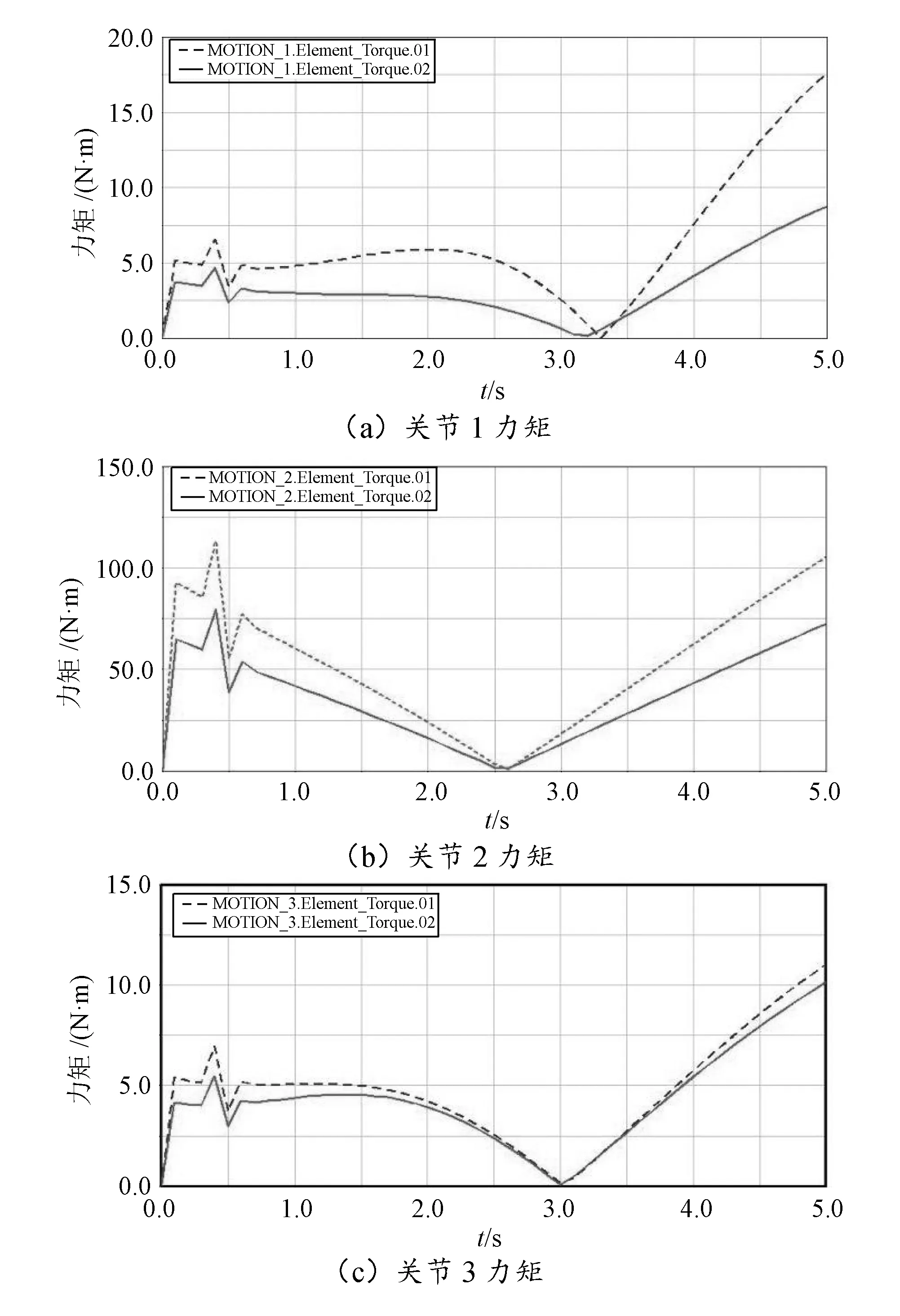
图8 优化前后关节驱动力矩对比

通过对比可知，当机器人末端执行器到达b1点时，优化算法后关节1,2和3的最大力矩相较于任务空间在优化前各减少8.818 0 N·m、34.403 6 N·m和0.874 2 N·m；从整个过程来看，工件坐标系在优化后的坐标系上时，机器人前3个关节的力矩都相对较小，由此可以看出，任务空间的基坐标系在优化后的坐标上时切削机器人的动力学性能更好。

5 优化结果分析

以优化结果(xw，yw，zw)=(0.521 5，-0.468 9，-0.256 8)为工件坐标系原点，铣刀沿y方向移动，切削点在工件坐标系中从(-1,0,0)到(-1,1,0)，在这个过程中，六自由度切削机器人关节角位移、关节角速度和角加速度的变化情况如图9所示。

通过图9(a)可以看出，各关节角位移曲线较为连续，变化幅度较小。图9(b)为关节角速度随时间的变化曲线，曲线较平滑，没有明显拐点。图9(c)为角加速度曲线，图中反映出的各关节角加速度变化较为平稳、连续。从图中可以看出，最大的角速度出现在关节4上，其值为-49.049 2 (°)/s，最大的角加速度为关节6的-58.483 2(°)/s2。最大角速度小于切削机器人关节4允许的最大角速度250 (°)/s，满足六自由度串联切削机器人对各关节的角速度和角加速度要求。

6 结束语

本文在获得六自由度切削机器人三维模型的基础上建立了其动力学模型，以各关节力矩和最小为目标函数，通过遗传算法得到了任务空间相对于机器人基坐标系的优化位姿参数。仿真结果表明，任务空间在优化后的坐标系上时，机器人各关节角位移、角速度和角加速度的曲线平稳、连续，末端执行器在任务空间的最远端b1点时各关节力矩均较小，动力学状态较好，达到了任务空间动力学优化的目的。本文的计算过程适用于多自由度机器人优化位姿的求解，也为多自由度切削机器人的动力学研究提供了一种较好的优化办法。