堆积体三轴试验及离散元模拟研究★

潘鑫鹏 鹿守山 田 海

(1.南昌工程学院，江西省水利土木工程基础设施安全重点实验室，江西 南昌 330099； 2.江西省交通科学研究院，江西 南昌 330200)

在我国很多地区都有广泛的松散堆积体发育，物质成分包括土夹砾石或块石以及块石夹土等，其结构松散、稳定性较差，粒间结合力差、透水性强[1]。堆积体的衍生地质灾害具有随机性和多发性特点，引起了岩土工程、工程地质等学科的广泛关注。目前揭示堆积体地质及整体稳定性的研究成果较多。赵建军、巨能攀等[2]采用二维有限元研究了西南地区某松散堆积体工程边坡开挖变形机理。从细观结构来看，岩土结构可被看作由单粒、粒簇或凝聚等骨架元构成的空间体系，单元状态决定了粒间的传递性能及变形性质；岩土结构强度及稳定性则通过其连接方式和排列方式来确定。松散堆积体的表观变形主要源于粒间位置的变化，而非颗粒本身的压缩而导致。自1979年Cundall.P.A首次提出细观颗粒流方法(Particle Flow Code)[3,6]以来，国内外众多学者已经开展了相当多的岩土应用研究[4，5]。本文以西南绵竹地区地震带广泛发育的松散堆积体为研究对象，通过对其进行系列大型三轴压缩试验研究强度及变形特性。在室内试验结果基础上，利用三维离散元颗粒流理论，基于PFC3D平台建立了典型堆积体三轴试样相对应的细观数值模型，通过内嵌语言二次开发模拟了三轴固结排水试验过程。通过对比颗粒流数值计算结果和室内三轴试验结果，从细观角度解释堆积体的强度和变形机制。

1 颗粒流基本理论

颗粒流理论(PFC)是基于非连续介质力学的细观分析方法，通过离散单元模型来模拟颗粒介质的运动及其相互作用，研究颗粒介质的运动及特性，解决复杂变形和大变形模式下的实际问题[3]。PFC通过中心差分法进行动态松弛，各时步遵循牛顿第二定律和力—位移定律，迭代并遍历整体集合。每个接触点的相对运动则由力—位移定律计算得到，最后通过接触模型来更新每个接触力[11,16]。

1.1 颗粒黏结接触模型

接触通常被两种黏结模型BPM(Bonded-Particle-Model)[6]描述：接触黏结模型(Contact-Bond-Model)和平行黏结模型(Parallel-Bond-Model)[8,14]。堆积体的单元颗粒形状不规则、多棱角、颗粒排列紧密，本文在BPM模型基础上，通过引入Clump颗粒单元来对比颗粒形状对宏观力学性质的影响，不同大小的Clump单元内部的颗粒可以任意重叠，不产生接触力，在Clump产生或颗粒添加到Clump的过程中其颗粒原有的接触力被保存并在计算循环过程中保持不变，此举在一定程度上提高了计算效率[9,12]。

1.2 宏细观参数之间的关系

岩土体宏观与细观力学参数存在高度非线性，宏细观参数之间没有明确的函数关系。因此，PFC细观力学参数的确定主要是通过与试验结果的误差分析实现[8]。在建立的颗粒流数值试样模型里，赋予模型假定的细观力学参数进行数值试样试验，并将计算得到的试样宏观力学参数与真实试验结果对比，当计算结果与试验结果基本一致时，便可将该组试样的细观力学参数推广应用于该类对象体的其他数值计算模型，过程需要按相应方向反复迭代调整细观力学参数最终获取期望的宏观力学参数。

2 堆积体大型三轴固结排水试验

2.1 试验材料及制备

试验松散堆积体为绵茂公路带广泛发育的山坡坡积体，细粒含量相对较少，粗粒石主要为灰岩，颗粒结构存在着大小不同的孔隙，同时颗粒本身存在细微孔隙。

试验采用结合缩尺法进行制样，现场测得原始级配及相似级配处理的级配数据如图1所示，颗分试验结果表明，试样中大于10 mm的粗颗粒物质占60%以上，试样属级配不良的粗颗粒岩土。由于试验条件限制，制样过程采用相似级配法对粒径大于60 mm的大颗粒进行置换。试验所用松散堆积体的天然物性参数见表1。

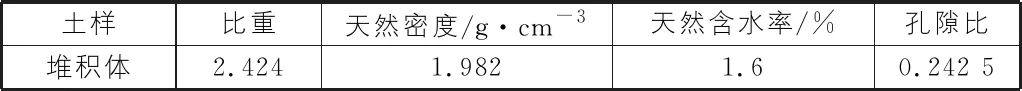
表1 堆积体物理力学参数

2.2 试验仪器与方法

试验采用大型应力式高压三轴仪GSZ501，试样尺寸为30 cm×60 cm。根据试验要求的干密度试验尺寸和级配曲线制样，进行固结排水剪切试验，剪切速率为0.6 mm/min，轴向应变速率为0.1%/min。试样围压分别为0.2 MPa，0.4 MPa，0.8 MPa，1.0 MPa。

3 堆积体三轴试验的数值模拟

3.1 颗粒流数值试样的生成

首先建立确定的空间结构容纳颗粒体，包括内壁光滑无摩擦的柔性圆筒用于施加围压，以及刚性平板对圆筒两端约束并施加轴向荷载，在既定颗粒参数和随机分配算法的前提下生成颗粒体试样[11]。堆积体三轴数值模型试样尺寸(圆柱体)：高60 cm，直径30 cm。将堆积体试样描述为均一介质的球形颗粒集合体，根据试样级配曲线和制样孔隙率，按照各粒组含量逐一生成颗粒，生成的各粒组质量百分比可以等价于体积百分比，得到与室内试验材料级配一致的颗粒集合体。生成集合体过程中，需要注意的是实际堆积体最小粒径为0.1 mm，若直接生成将产生颗粒数目惊人的模型，十分耗费计算资源，而最小颗粒对数值精度的贡献又不太大[11,13]，鉴于此，控制数值模型颗粒集合体最小粒径为1 mm，粒径分布见表2。利用少数球体随机生成两种Clump颗粒单元模拟堆积体中不同形状的颗粒单元，得到的PFC3D颗粒集合体如图2所示。

表2 数值试验的颗粒级配

3.2 细观参数的标定

表3 堆积体细观力学参数

3.3 数值试验的实现

数值模拟过程经由等压固结、控制围压，固定速率加载等环节，使试样在每一步的平衡状态下加载，直至轴向应变达到三轴试验破坏对应应变值，加载过程停止。本文通过用标定的细观参数在各围压工况下进行数值试验，得到各级围压下偏应力—轴向应变(q—εa)以及体变—轴向应变(εv—εa)曲线，结果与室内试验曲线对比如图3所示。

4 数值模拟与试验结果对比分析

4.1 应力—应变特性对比

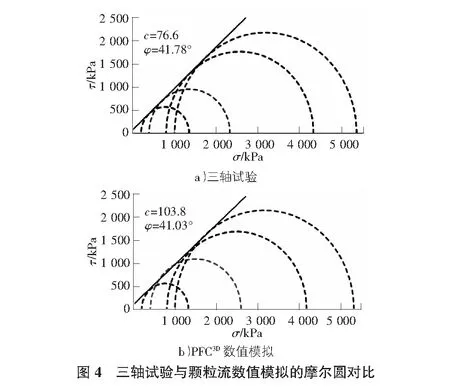
室内大三轴试验结果表明(见图3)，4组试验应力—应变曲线表现出不同的形式，随着围压的增大，堆积体强度特征由应变硬化型逐渐转变为应变软化型，峰值剪应力强度在轴向应变持续增长过程中出现的更晚。对比三轴试验结果相，引入Clump颗粒单元的数值试样近似模拟了堆积体颗粒集合的不规则性，得到的应力—应变曲线和室内试验结果较为一致。其中，数值试样在各围压下的峰值强度相对较高，体现在摩尔应力圆中为粘聚力较室内试验值高，而摩擦角的影响较小，如图4所示。

4.2 体变—轴向应变特性对比

堆积体在排水剪切过程中均出现了明显的剪胀现象，由初始的剪缩发展到剪胀，但随着围压的加大，剪胀程度逐渐变小，这主要是由于高围压下三轴试样径向约束增强，堆积体颗粒间翻越阻力增大，从而体胀能力减弱。对比堆积体三轴试验与数值模拟结果，存在一些不同，数值试样εv—εa曲线中初始段剪缩到开始剪胀的拐点相对于试验曲线在低围压时出现的更早一些，高围压则推迟了，但总体上此数值模拟结果与三轴试验曲线趋势基本一致。

5 结语

1)堆积体三轴排水剪切试验随着围压的增大，堆积体强度特征由应变硬化型逐渐转变为应变软化型，峰值应力强度在轴向应变持续增长过程中出现的稍晚。与试验结果相比较，数值试样在各围压下的峰值强度相对较高，在低围压情形下的初始切线模量Ei相比室内试验结果偏大，偏应力—应变曲线和室内试验结果基本一致。2)堆积体在排水剪切过程φ均出现了明显的剪胀现象，由初始的剪缩发展到剪胀，但随着围压的加大，剪胀程度逐渐变小。数值试样εv—εa曲线中初始段剪缩到开始剪胀的拐点相对于试验曲线在低围压时出现的更早一些，高围压则推迟了，但总体上此数值模拟结果与三轴试验曲线趋势基本一致。3)颗粒流离散数值模型应用于模拟堆积体=三轴试验，有利于扩展试验条件的范围，对比更多工况的试验数据，弥补了实体试验的功能限制。但对于数值试样来讲，通过单一球体单元模拟整体结构，对复杂细观结构的真实岩土材料来说反映机理有待深入研究，需进一步对颗粒流程序算法进行二次开发使其能在模拟过程中建立不规则的颗粒单体。