基于Copula-CVaR的农场利润与经济风险统计方法

党荣

摘要：针对农场的作物产量及农业收入受到多方面因素的影响，提出了一种用于计算农场利润和经济风险的统计模型。该模型在已有统计理论的基础上采用条件风险值（CVaR）来评估地理多样化的有效性。CVaR用于基准化损失，Copula函数用于建模边际收益之间的联合分布。结果表明，地理多样化对于小麦农场投资组合是可行的农业风险管理方法，可以在控制风险的同时实现其最佳预期收益。通过与传统的多元正态分布模型相比，基于Copula的均值CVaR模型更能模拟极端损失，为农业风险管理提供了新的思路。

关键词：农场利润;地理多样化;CVaR;Copula函数;投资组合

Abstract： A statistical model for calculating farm profit and economic risk was presented in view of the influence of various factors on farm crop yield and agricultural income. On the basis of the existing statistical theory， the model used the conditional value-at-risk （CVaR） to evaluate the effectiveness of geographical diversification. CVaR was used to benchmark losses， while the Copula function was used to model the joint distribution of marginal revenues. The results showed that geographic diversification could be a feasible agricultural risk management method for wheat farm portfolio managers， which could achieve the optimal expected returns while controlling the risk. Compared with the traditional multivariate normal distribution model， the average CVaR model based on Copula could better simulate extreme losses， providing an innovative solution for agricultural risk management.

Key words： farm profit;geographical diversification; conditional value-at-risk （CVaR）; Copula  functions; portfolio

气候多变性极大地影响了农业生产以及农业收入。据统计，发展中国家约1/4的农业生产受损与极端气候相关的灾害有关，极端干旱也会导致农作物产量显著下降[1]。为了减轻并尽可能减少极端气候事件引发的农业产量和相关财政损失，需要采取农业适应战略。

经典的均值方差投资组合优化通过对有效投资组合进行优化，以最大程度地减少方差并降低总体财务风险[1]。尽管经典的均值方差方法被广泛应用，但它也有局限性。例如，方差度量是一种不考虑共同运动方向的对称度量[2]。将方差最小化以与投资组合收益分布的上行风险相同的方式惩罚下行风险是一个问题，因为相对于收益低于预期的资产，收益高于预期的资产被认为是一种风险状况。为了解决这个问题，引入了其他基于风险的度量方法，如用风险值（Value-at-risk，VaR）和条件风险值（Conditional value-at-risk，CVaR）来代替经典的均值方差方法。研究推荐CVaR作为替代风险的衡量标准，因为基于CVaR的优化投资组合只会对损失（即下行风险）进行惩罚，而不对收益（即上行风险）进行惩罚[3]。

基于历史数据的模拟方式假设未来收益的分布与过去相似，且在大多数情况下数据点相对较少。因此，使用蒙特卡洛方法，以类似于历史模拟的方式计算CVaR，同时也基于从历史数据中获取参数的模型随机生成方案。与传统方法相比，需要更有效地捕捉边际收益尾部的非线性相互依赖关系，以获得对CVaR的准确估计。传统的方法通常依赖于使用多元正态分布模型（M-normal），该分布假定所考虑的变量是正态的。然而，农产品价格和作物产量已经被证明是非正态分布，因此，任何不考虑这一重要数据限制方面的方法都可能导致错误的结论。Copula函数可以分析多元数据中的非线性，能够提供一种替代的统计方法来建模多元数据集的联合分布，从而允许人们独立地指定被测变量之间的边际分布及其依赖结构。基于Copula的模型因在多元联合分布建模方面的独特优点，已广泛应用于许多领域，如保险和金融风险建模[4，5]、水文与水资源[6]、发电站可靠性分析[7]以及农业和降水预报[8，9]。

虽然Copula方法在一般的金融风险研究和投资组合分析中是一个被广泛应用的工具[10]，但在农业风险管理和农作物保险方面的应用相对较晚。尽管如此，这些研究也特别值得借鉴。例如，赵玉等[11]提出了基于混合Copula模型的水稻保险费率厘定，该方案借助核密度估计方法和混合Copula模型研究了水稻产量和价格风险因子的联合分布，同时还厘定了产量、价格和收入3种保险的纯费率;王国栋等[12]研究了基于Copula函数的经济作物收入保险费率测算方法，该方法以甘肃省苹果为研究对象，运用Copula函数和蒙特卡洛方法测算了不同保障水平下的收入保险费率，提出了包括制定差异化费率、控制高保障水平下保费补贴比例等建议;Larsen等[13]提出了一种Copula的均值CVaR模型，以美国小麦种植业为例，考察采用地理多样化战略降低风险的潜在收益。该文献应用多元阿基米德Copula模型，并将其与传统的多元正态模型作为基准工具进行了比较。从农场边际收益的角度来看，均值CVaR优化结果表明，地理多样化在風险管理策略中是有效的。多元正态分布模型导致在给定的农业盈利水平下低估了农场面临的最低相关风险水平。然而，迄今为止，地理多样化战略在农业中的有效性研究较少。为了解决这一需求，特别是对于农业依赖的国家，本研究调查了地理多样化在小麦种植的投资组合管理中的效用，旨在分析地理多样化战略在降低农业经营风险中的有效性。为了证明基于Copula的均值CVaR模型是一种稳健的统计方法，将其用于量化给定风险水平所需的最佳多样化数量，并比较了传统多元正态分布模型和Copula模型在极端损失模拟中的差异。

1 方法论

由于中国小麦种植范围较广，种植区地理多样化的有效性，包括风险管理策略中的均值CVaR优化，还未在农业环境特别是小麦栽培区域中得到检验。因此，本研究在模拟方法中利用Copula方法来计算相应的CVaR值。该方法允许根据联合分布随机生成农场边际收益的情景。

以某省3个不同地理区域的农场为例（分别命名为KF、ZK、NY），以农场盈利能力衡量的边际收益，即总收入超过总成本占总收入的比例表示。第[i]个区域的边际收益[ri]（[i]=1，2，3）计算如下：

1.1 条件风险值

假设[f（x，y）]表示一个取决于决策[x]的损失函数，该决策将从现实投资组合的可行集合X和随机向量[y]中选择。令[Ψ（x，α）]的损失函数[f（x，y）]不超过某个阈值[α]的概率。VaR函数[αβx]是在置信度[β]处的损耗分布百分位数，定义为：

式中，[p（y）]为随机向量[y]的概率密度函数，可以看出，在相同的置信水平下，CVaR是VaR的一个较大的界。CVaR提供了比VaR更一致的风险度量，并且通常在投资组合优化的环境中能得到更有效的结果。此外，CVaR可以表示为一个凸函数，允许构建投资组合优化问题，该问题可以通过线性规划技术被有效地解决。虽然VaR在最优投资组合方法中起到了一定的作用，但也暴露了一些内在的限制。因此，高损失的风险可以通过最小化CVaR而不是最小化VaR来降低，因为一个低CVaR的投资组合也必须有低的VaR[14]。

1.2 投资组合优化问题

假设1个投资组合由[n]个生产区域组成，边际收益[r1，...，rn]为随机百分比，边际预期收益[E[ri]]是分配给生产区域的总面积，[wi]是决策向量或权重。在农业部门的背景下，农场的投资组合优化问题是在给定的特定风险水平[β]的情况下最大化投资组合的预期收益（所有边际预期收益之和乘以相应权重）。投资组合优化问题可以表述为：

1.3 计算条件风险值

1.4 Copulas函数

如上所述，使用蒙特卡罗模拟法计算CVaR需要了解投资组合中所有边际收益的联合分布[15]。为了满足这一要求，建议将联合分布函数[F（x1，...，xn）]表示为：

2 结果与分析

为解决基于最优Copula统计模型的农业投资组合优化问题而生成的模型结果，下面在应用模型和相关问题的背景下提供了物理解释。与极端气候条件有关的边际收益的波动首先被描述出来。Copula模型选择的结果将用多元Copula函数来描述，并建立了传统的多元正态分布模型，且对二者进行了比较。最后， 讨论了均值CVaR优化和最优投资组合分配结果，这些结果来自不同置信水平的模型。图1显示了每个小麦种植区的历史边际收益。边界收益的增加和降低表明，对应农业区可能有潜在的高收益率，但也可能有潜在的极低收益率。因此，从汇总统计数据分析得出的直观结论是，在ZK种植小麦可能会获得更稳定的效益，并降低一些风险。

2.1 Copula模型

作为模型构建的第一步，将历史边际收益拟合到理论分布曲线上。3种历史边际收益数据都可以用广义逻辑分布进行适当描述，估计参数包括密度、累积分布函数、分位数图、概率图，通过对这些参数的分析来确定边际分布结果。在建立最優Copula统计模型之后， 应用基于Copula的蒙特卡罗仿真，并从选定的每个区域获得了2 700个边际收益的模拟，即对27个样本的样本量进行了100次重复模拟。为了便于比较，研究还使用了传统的多元正态分布模型来生成另一组使用蒙特卡罗模拟技术的模拟数据。在这种情况下，假定边际收益服从多元正态分布，即单个边际收益分布及其依存关系被假定为正态，这3组随机模拟的数据（已转化为真实值）最终用于地理多样化分析和解释。

2.2 平均CVaR有效边界

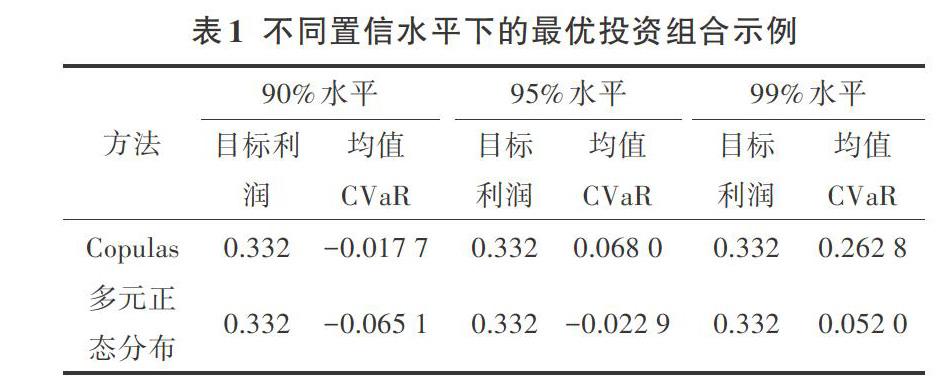
在目标风险约束下，对期望收益最大化的农场投资组合的均值CVaR进行优化。表1显示了3种常见置信水平下的最优投资组合示例（即置信水平分别为90%、95%和99%）。根据定义，CVaR风险度量将结果与0进行比较，因此它可能有正值和负值。

为了比较不同分布假设下均值CVaR的最佳值，为每个置信水平选择了预期收益的相同目标。基于Copula的投资组合比传统的多元正态分布投资组合产生了更高的均值CVaR。因此，表1的结果表明，如果边际收益的联合分布正确地遵循由Copulas建模的非正态分布，则农场主很可能低估了通过均值CVaR衡量的最小风险水平给定的预期收益。由于边际收益明显不符合正态分布，因此应根据Copula模型来衡量风险水平。

从图2可以看出，与多元正态分布模型相比，基于Copula的模型边界值明显更高。这是因为基于Copula的模型能够考虑到尾部的相关性，而多元正态分布假设尾部相关性系数为零，因此忽略了联合分布尾部的共同运动。因此，依赖传统多元正态分布假设的投资组合优化方法可能保护效果较差，而基于Copula的模型更适合那些担心自己的农场盈利能力遭受极端损失的农场。由此可以推断，在所有考虑的置信度水平上，Copula能够比多元正态分布模型更好地衡量风险。这是因为，通过构造方法，Copula比多元正态分布模型更灵活地对每个变量对的依赖关系进行了建模。为了检验这一点，还检验了2种模型的保存能力，以模拟变量对之间的依赖关系。显然，与多元正态模型相比，Copula方法能够保留所有变量对的依赖性。

相对于基于Copula的边界，每个区域的单一投资组合如图3所示。由图3可以看出，目前在KF和NY地区种植小麦的农民的盈利能力低于有效边界水平，而ZK区则处于边界曲线上。在给定的下行风险水平下，地域多元化可能会提高KF和NY区的盈利能力，但不会提高ZK区的盈利能力。因此，在ZK种植小麦可能面临最大的风险，因为它位于边界曲线的最高点，但是也有可能达到最高的获利能力。此外，在这种情况下，生产商可能会决定通过地理多元化来降低利润率，以降低相对较大的下行风险。

3 结论

使用基于Copula的方法计算了均值CVaR，与传统的多元正态分布模型相比，Copula统计方法能够灵活地对包括非正态分布在内的不同类型边缘数据集的联合分布进行建模。使用蒙特卡罗模拟方法中的场景来计算CVaR标准，并通过最大化给定目标水平CVaR的预期边际收益来实现投资组合优化。因此，基于Copula的模型更适合于评估农场盈利能力以及经济风险。

参考文献：

[1] 刘燕武，张忠桢. 基于实际收益率分布的均值-方差-条件风险价值多目标投资优化模型[J]. 系统管理学报，2010，19（4）：444-450.

[2] 张保帅，姜 婷，周孝华，等. 投资组合优化的新方法：Mean-CoVaR模型[J]. 统计与决策，2019，35（11）：67-70.

[3] 石珂琦. 基于预测值-CVaR风险度量的投资组合优化模型[J]. 中南财经政法大学研究生学报，2015（5）：22-29.

[4] 游翔宇. 基于pair-Copula情景生成的CVaR投资组合模型研究[D]. 合肥：中国科学技术大学，2017.

[5] 黄 瑞，吴鑫育. 基于Copula-GARCH模型的最小VaR套期保值比率的估计[J]. 伊犁师范学院学报（自然科学版），2017，11（4）：18-22.

[6] 孔祥铭. 基于Copula分析的水资源系统风险评估与管理方法研究[D]. 北京：华北电力大学（北京），2016.

[7] 王 敏，茅鑫同，王鹤梅，等. 基于Copula理论考虑光伏出力与负荷相关性的含光伏电站发电系统可靠性分析[J]. 科学技术与工程，2016，16（4）：54-59.

[8] 曹伟华，梁旭东，赵晗萍，等. 基于Copula函数的北京强降水频率及危险性分析[J]. 气象学报，2016，74（5）：772-783.

[9] NGUYEN-HUY T， DEO R C， MUSHTAQ S， et al. Modeling the joint influence of multiple synoptic-scale，climate mode indices on Australian wheat yield using a vine copula-based approach[J]. European journal of agronomy，2018，98：65-81.

[10] 董立宽，方 斌，王晨歌. 基于Copula函数的茶园土壤铜锌空间协同效应研究[J]，自然资源学报，2018，33（5）：867-878.

[11] 赵 玉，严 武，李 佳. 基于混合Copula模型的水稻保险费率厘定[J]. 統计与信息论坛，2019，34（8）：66-74.

[12] 王国栋，庞 楷. 基于Copula函数的经济作物收入保险费率测算——以甘肃苹果为例[J]. 金融理论探索，2019（3）：62-70.

[13] LARSEN R， LEATHAM D， SUKCHAROEN K. Geographical diversification in wheat farming： A copula-based CVaR framework[J]. Agricultural finance review， 2015， 75（3）：368-384.

[14] 张 冀，谢远涛. 风险依赖、一致性风险度量与投资组合——基于Mean-Copula-CVaR的投资组合研究[J]. 金融研究，2016（10）：159-173.

[15] 柴尚蕾，周 鹏. 基于非参数Copula-CVaR模型的碳金融市场集成风险测度[J]. 中国管理科学，2019，27（8）：1-13.