变形机翼前缘柔性蒙皮优化设计与分析
王志刚, 杨宇
(中国飞机强度研究所,陕西 西安 710065)
0 前言
随着全球民用航空工业的蓬勃发展,乘坐飞机出行的乘客数量快速增加,导致民用航空对环境的挑战日益增大。为解决该问题,大部分国家及地区对民用飞机的耗油量及噪声等都提出了更高的标准[1-2],设计新一代飞机机翼结构成为满足该要求最有效的手段之一。可变形的机翼前后缘结构能够根据飞机的飞行任务(巡航、起飞和降落等)和外界条件(马赫数和高度等)的不同改变气动外形,实现气动外形实时优化,提高飞机的气动效率,降低燃油消耗率。无缝光滑的气动表面能够降低由于结构尖锐部分和空气摩擦产生的噪声,提高民用飞机的舒适性。此外,高质量的气动表面能够推迟气动的分离,有利于层流飞行。因此,连续无缝的变形机翼前后缘结构是未来民机发展的重要趋势[3-4]。
实际上,变弯度机翼并不是一种全新的概念,1973年莱特兄弟驾驶的有动力固定翼飞机就应用了无缝光滑的变弯度后缘结构。该飞机后缘采用一体化的帆布蒙皮,通过对后缘的拉和推实现了蒙皮的翘曲变形,进而实现对飞机的飞行控制。随着飞机飞行速度和服役环境复杂度的提高,这种直接拉动蒙皮变形的驱动方案无法在金属蒙皮飞机中实现。因此,现代飞机都采用了固定外形的结构方案,它们只能通过前缘和后缘的刚性偏转来实现起飞和降落的控制,并不能实现翼型的实时最优。
随着结构设计方法、材料和控制等技术的成熟,使变弯度机翼的实现成为了可能,越来越多的高校和研究机构再一次关注该领域,并尝试了多种变弯度机翼的结构方案。他们根本的目的在于解决变弯度机翼高承载和可变形的矛盾,实现变弯度机翼前缘无缝光滑的连续变形。1985~1988年,美国空军和NASA联合开展了F-111任务自适应机翼(MAW)的设计与验证技术研究,实现了变弯度机翼的飞行测试,验证了可变形机翼的气动优势。但结构重量的急剧增加限制了该结构方案的应用。1994~2007年,美国国防科技创新计划局(DARPA)发起了智能机翼(Smart Wing)、变形飞机结构(MAS)等项目,开发了变弯度机翼样机,并进行了风洞试验。目前,较为成熟的方案是德国宇航院(DLR)在SARISTU项目中开发的基于连杆机构的自适应前缘下垂(EADN)装置[5-8]和美国Flexsys公司设计的基于柔性结构的自适应柔性后缘(ACTE)[9]。2015年,DLR完成了EADN的地面试验验证,并评估了其综合效益及安全性,效果良好。2017年,Flexsys进行了ACTE Ⅱ的飞行测试,并实现了空中连续的弯度偏转。总体来看,变弯度机翼的实现方案主要分为两类:刚性机构与柔性结构组合方案和全柔性结构方案。基于柔性结构的变弯度机翼方案难以满足大型飞机驱动力要求和气动弹性等要求,成熟度较低。而基于传统刚性机构与柔性结构的组合方案能够较好地解决该问题,易于满足大型飞机的应用要求,是目前较容易满足适航要求的方案。
本文以CAE-AVM远程公务机为应用对象,提出了一种无缝光滑的变弯度前缘结构方案及柔性蒙皮优化设计方法,并提出了一种改进的变形控制问题目标函数描述方法。该方法中柔性蒙皮采用了极限应变较大的玻璃纤维增强复合材料。
1 结构方案
机翼前缘在巡航、起飞和降落等状态下都需要承受较大的气动载荷,因此变弯度机翼前缘在展向应具有较大的承载能力,必须有类似于竹帘式的结构对蒙皮进行展向加强,且外部气动载荷需要可靠地传递至主翼盒结构。同时,为了实现弦向变弯度,蒙皮还应该满足弦向的大变形要求。因此,为达到上述要求,本文提出了一种基于连杆机构的变弯度机翼前缘结构方案。该方案主要由复合材料柔性蒙皮、连接长桁、驱动机构、驱动器等组成(图1)。

图1 基于连杆机构的变弯度机翼前缘结构方案
为实现前缘蒙皮精确变形控制,设计过程中需要解决四大问题:外部柔性蒙皮刚度分布的优化设计;内部驱动机构拓扑的优化设计;变弯度前缘协同控制系统设计;变厚度复合材料蒙皮的加工。
首先,与样条曲线的生成原理类似,柔性蒙皮的目标外形本质上是通过4个控制点进行全局控制,而局部精确外形控制需要通过调节蒙皮刚度的分布来实现,初始的外形则通过复合材料成型时的模具保证。因此在外部柔性蒙皮设计过程中,重点需要解决长桁位置和蒙皮刚度分布的优化设计问题。其次,当长桁位置和蒙皮刚度确定时,蒙皮的实际轮廓由长桁连接铰点的空间轨迹决定。因此为了实现长桁连接铰点的轨迹控制,需要对内部驱动机构的拓扑进行优化设计。再次,对于真实的三维变弯度机翼前缘结构设计时,还需考虑多个驱动翼肋的协同控制问题。最后,变厚度复合材料的蒙皮制造也是此类变弯度前缘结构实现的一大挑战。
2 气动外形的定义
本文的应用对象CAE-AVM为洲际喷气式公务机,采用尾吊式双发动机,巡航马赫数为0.85,并采用了高展弦比超临界机翼。经分析,采用变弯度机翼前后缘,能够有效提高CAE-AVM的巡航能力,并降低噪声。因此本文以CAE-AVM为参考飞机,并取外翼靠近舷窗的翼型剖面(展向离机身约30%处)作为参考翼型。该机翼实际为具有根梢比和后掠角的机翼,但作为方法验证,本文取参考翼型生成的等直机翼,进行无根梢比和无后掠角的变弯度机翼前缘柔性蒙皮优化设计。
与后缘实现变弯度的机理不同,前缘的变弯度是通过蒙皮整体滚动实现的。因此,如果能够进行合理的设计,保证蒙皮在滚动过程中长度始终不变,则可以极大的降低蒙皮的面内应变,提高蒙皮的变形能力。因此,在进行目标气动外形优化设计时,应增加蒙皮长度不变的几何约束,从而实现气动结构协同优化。本文所用翼型的优化设计即考虑了该约束。该优化过程以前述的CAE-AVM飞机巡航状态下的翼型剖面作为初始设计外形,以起飞和降落条件下升阻比最高为优化目标,同时考虑长度不变的几何约束,通过CST参数化方法进行气动外形的描述,并采用基于梯度的优化算法确定了最佳气动外形。图2给出了前缘的初始外形和经过优化后的目标形状。
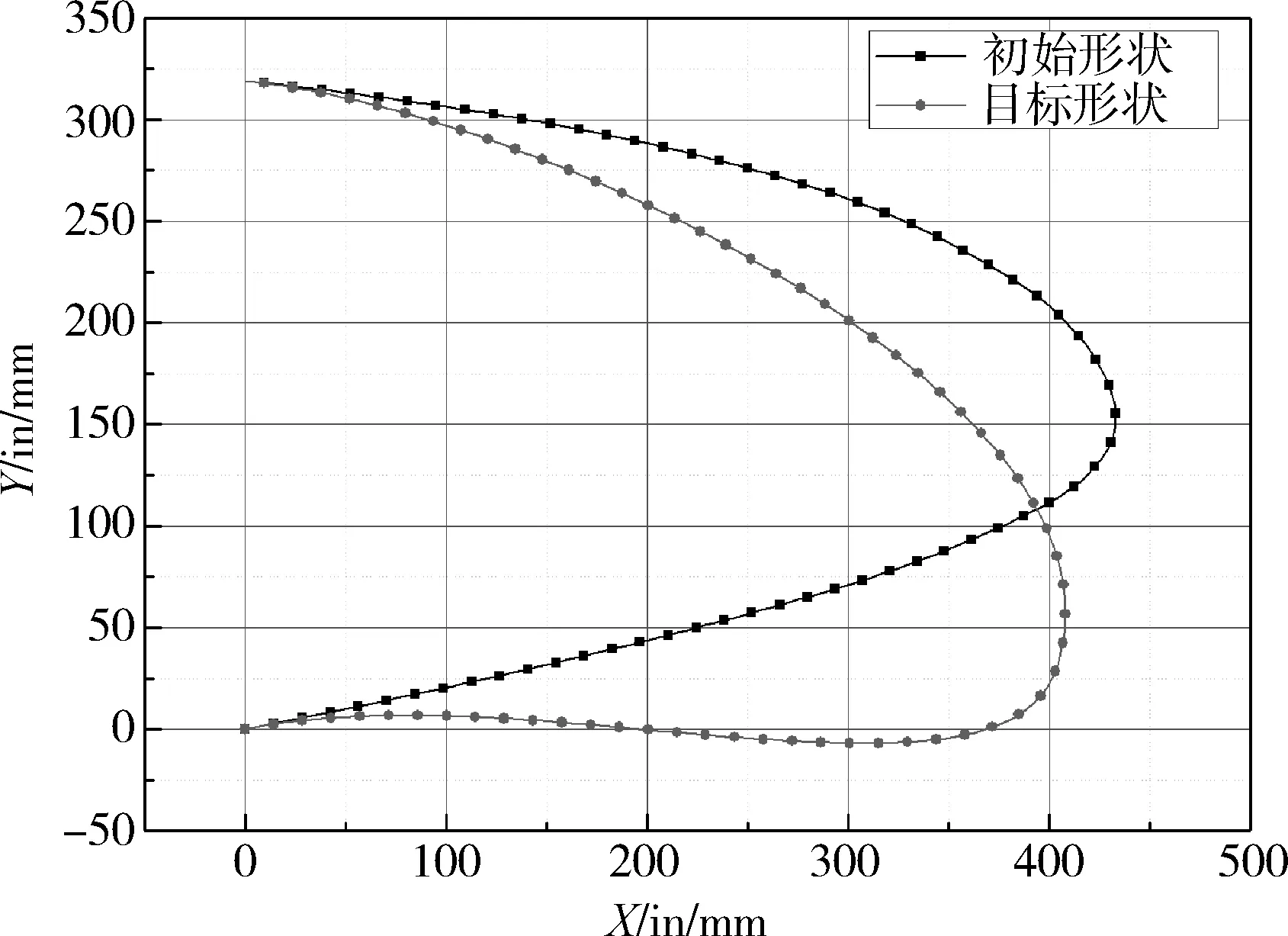
图2 前缘初始形状与目标形状
在长度不变的设计理念下,蒙皮的应变主要由弯曲应变产生,并且弯曲应变与曲率变化和厚度有关。为了保证前缘蒙皮的结构完整性,下垂过程中蒙皮的最大应变不能超过材料的极限应变。根据材料力学可知,蒙皮弯曲变形时,蒙皮表面的弯曲应变最大,最大应变、曲率变化和允许的最大蒙皮厚度三者之间关系如式(1)所示:
(1)
式中:s——蒙皮周向局部坐标;
t——允许的最大蒙皮厚度沿周向分布的函数;
εlim——蒙皮材料极限应变;
Δκ——蒙皮曲率变化沿周向分布的函数。
3 柔性蒙皮优化设计
3.1 目标函数
针对变形控制问题,一般的做法是通过变形前后曲线上的控制点坐标的最小平方差(LSE)进行目标函数的定义[10]。但前缘外形对蒙皮的表面质量要求较高,特别是靠近尖端的位置对气动效率的影响最大。如果简单地用LSE作为目标函数,有可能出现整体LSE较小,但局部误差较大的情况。因此,应该对越靠近尖端的蒙皮控制点进行误差的惩罚。基于此,本文提出了一种加权的最小平方差(WLSE)目标函数定义方法,如式(2)所示。
(2)
式中:n——控制节点数量;
wi——第i个控制点的加权系数;
di——第i个控制点目标位移;
xi和yi——第i个控制点实际坐标;
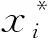
3.2 设计变量
如前文所述,长桁位置和内部驱动机构传递的力大小对蒙皮最终的宏观外形有较大影响。因此,为了实现柔性蒙皮在驱动条件下的精确变形,需要对长桁连接点位置和连接点力大小进行优化。此外,复合材料蒙皮刚度分布对前缘的变形精度也有较大的影响,它主要起到对蒙皮外形进行局部控制的作用,因此需要协同考虑蒙皮厚度与铺层的分布。关于铺层顺序,考虑到弯曲变形时蒙皮表面应具有较大的极限应变能力的要求,应将0 °(沿周向)铺层安排在最外层。同时,应将90 °(沿展向)铺层安排在靠内层,这样能够提高柔性蒙皮展向的弯曲刚度。以该原则为基础,本文事先定义了一组铺层顺序,并将每一个铺层的厚度(或者体积)作为设计变量,后期将进行考虑制造工艺的蒙皮铺层顺序调整。综上,变弯度机翼柔性蒙皮优化设计变量包括:蒙皮与内部机构连接点位置、连接点传递力大小、蒙皮各铺层厚度(图3)。最终,当上述变量确定后,蒙皮的变形则通过长桁连接点上的力驱动变刚度蒙皮从而实现整体的精确变形,相应连接点的位移及运动轨迹则可以作为后续内部驱动机构设计的输入。
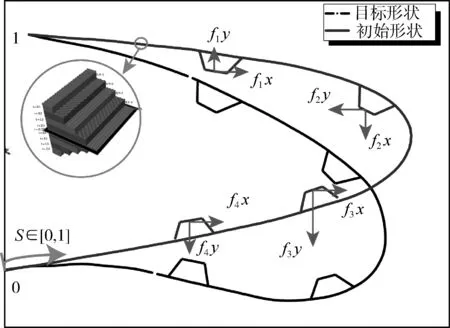
图3 柔性蒙皮优化设计的设计变量
3.3 优化约束
由前述分析可知,沿蒙皮周向,不同位置的蒙皮允许的最大厚度不一样。因此,为保证蒙皮最外层的结构完整性,在蒙皮厚度优化过程中,应针对每一个分区进行最大厚度的约束。其次,考虑到工艺要求,玻璃纤维层合板蒙皮各单层的厚度应该≥0.1 mm,且各方向铺层的总厚度为单层厚度0.1 mm的整数倍。
3.4 求解
综上,本文首先针对CAE-AVM变弯度前缘建立了结构有限元模型。理论上,变厚度柔性蒙皮的厚度分区数量越多,对蒙皮局部刚度的调整越有效,蒙皮的变形精度越高。极端的情况是蒙皮为一个连续的变厚度蒙皮,但这会极大地增加工艺的复杂性和成本,特别是对于复合材料。本文最终采用了10个厚度分区的数量建立蒙皮的有限元模型,如图4所示。考虑到蒙皮在巡航条件下需要抵抗气动载荷的要求,并根据前缘气动载荷分布的特点,本文初步确定采用4个长桁进行蒙皮的展向加强。层合板铺层采用了对称均衡的铺设方法,因此,每一个分区的设计变量减少一半,设计变量总数为68个。
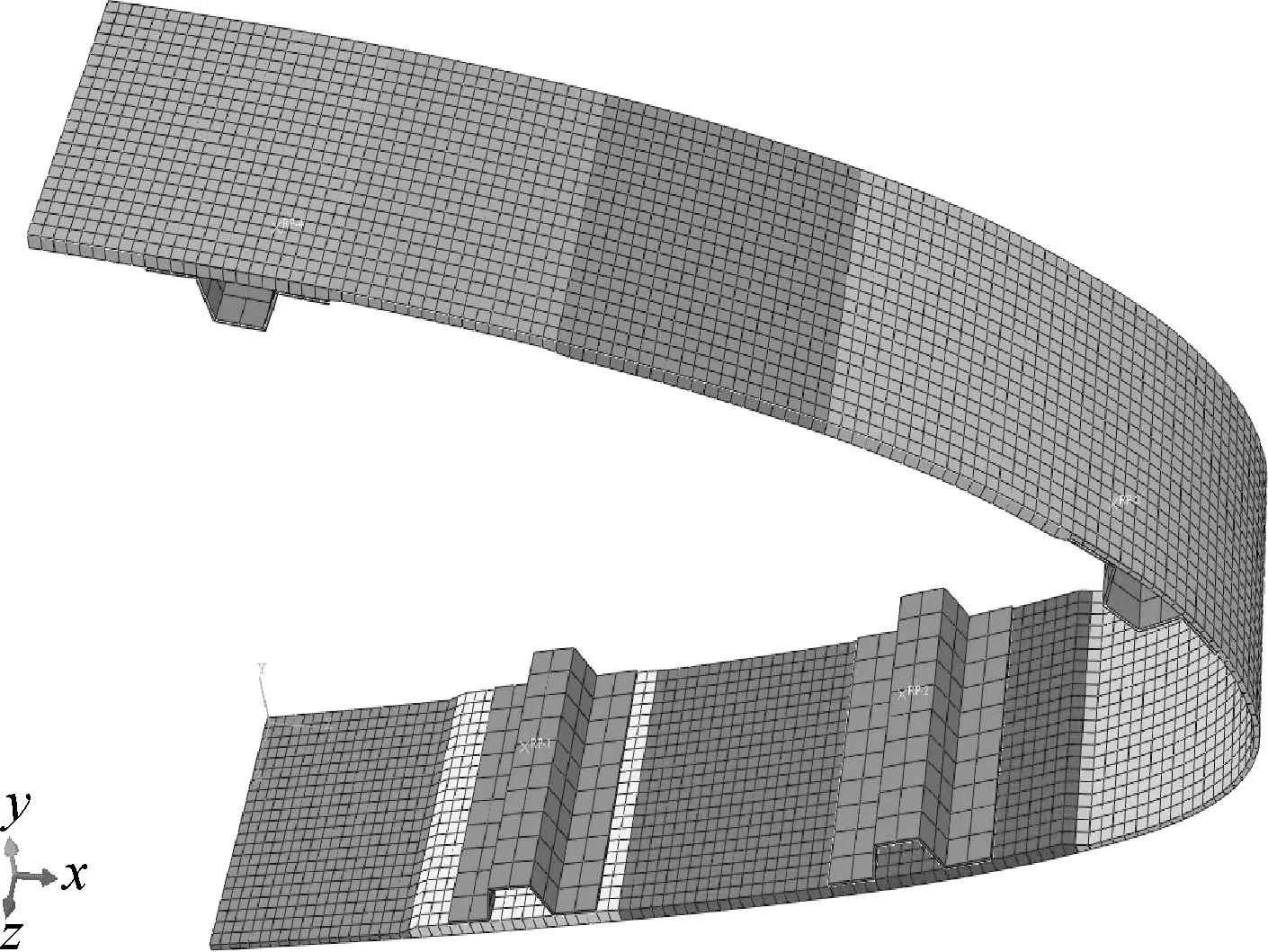
图4 蒙皮铺层的不同分区数量
在此基础上,为确定每一个分区的铺层厚度、长桁位置和长桁连接铰点驱动力的大小,本文针对玻璃纤维复合材料柔性蒙皮的优化设计问题建立了相应的数学模型,如式(3)所示:
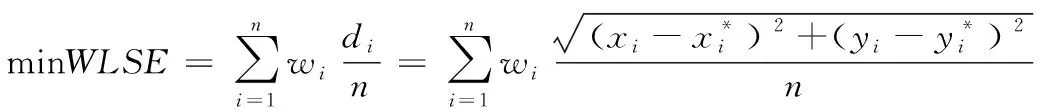
(3)
式中:si——第i个长桁的周向坐标;

fxi——第i个长桁连接点x方向力的分量;

fyi——第i个长桁连接点y方向力的分量;
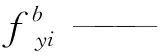

tij——第i个分区第j个铺层的厚度;
该数学问题涉及连续变量和离散变量,且优化问题复杂,基于梯度的优化算法难以求解该数学问题。因此,本文选择先进高效的进化算法进行优化问题的求解,即非支配排序遗传算法(NSGA-Ⅱ,Non-Dominated Sorting Genetic Algorithm Ⅱ)。经过133代的迭代计算,优化问题收敛。最终目标函数值为0.745 4 mm,即控制点的平均误差为0.745 4 mm。
优化结束后,可同时得到蒙皮各铺层厚度、长桁连接点位置和驱动力大小等三类变量的最优值,并且能够给出各长桁连接点的位移及运动轨迹。该运动轨迹可以作为后续内部驱动机构设计的输入。在长桁连接点位置处施加最优大小的传递力后,柔性前缘蒙皮实现了精确的变形,与目标变形吻合较好(图5)。

图5 前缘蒙皮初始形状、目标形状和实际形状对比
4 内部驱动机构设计
柔性蒙皮优化设计确定了蒙皮刚度的分布、长桁位置和长桁连接点的运动轨迹。在蒙皮和长桁确定的条件下,唯一影响蒙皮变形精度的因素是长桁连接点的位移。因此,需要设计一套能够精确实现连接点运动轨迹的内部驱动机构,以保证蒙皮的变形精度不小于蒙皮优化设计得到的结果。为此,本文基于上述优化设计结果,以最少驱动器为原则,并以实现长桁连接点运动轨迹为目标,提出了内部机构的概念,如图6所示。该内部机构由1根主杆和4根连接杆组成。主杆一端通过铰链与固定支撑装置A相连。4根连接杆一端与主杆铰接,另一端分别通过4个耳片与长桁铰接。当主杆受到绕固定点的旋转位移驱动时,主杆带动连接杆运动,并最终实现对蒙皮的变形控制。为了保证长桁4个铰点精确的运动轨迹,设计过程中应对内部驱动机构的连接铰点和固定点A的位置进行优化。作为初步设计,本文只提出内部机构的概念,正在进行其详细设计。
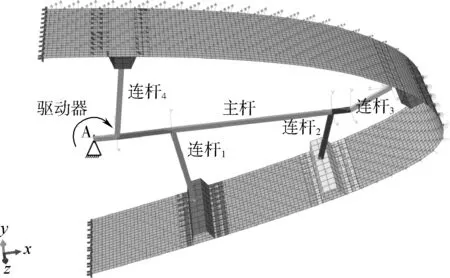
图6 内部驱动机构概念
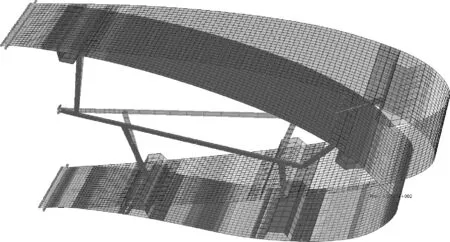
图7 下垂条件下蒙皮的应力分布云图
图7为柔性蒙皮在集成上述机构初步设计结果后的最终变形状态应力云图。分析结果表明,集成内部驱动机构后,在下垂状态下,蒙皮的最大应力集中在前缘尖端,约为378 MPa,但小于材料极限应力。作为机构的初步设计,其最终实现的变形有一定的误差,且集中在尖端的上表面,主要是由于连接点运动轨迹误差造成的。因此,后续将针对内部机构进行详细的优化设计,以提高连接点的运动轨迹精度。
5 结论
无缝连续光滑的变形机翼能够显著地提高民用飞机的综合性能,是未来民用飞机发展的必然趋势。本文以CAE-AVM远程公务机为应用对象,并以实现连续光滑的变弯度机翼前缘为目标,采用了基于连杆机构的变弯度机翼前缘结构方案,提出了四步法的设计流程和基于NSGA-Ⅱ的柔性蒙皮协同优化设计方法,综合考虑了复合材料蒙皮刚度分布、长桁连接点位置和连接点力大小等因素,实现了复杂变量的柔性蒙皮协同优化设计。分析结果表明,本文提出的WLSE目标函数能够有效地提高优化结果的精度,并验证了本文提出的蒙皮厚度自动修正约束的合理性与有效性。最终本文以蒙皮优化设计结果为输入,进行了内部连杆机构的概念设计,并实现了较精确的变形控制。研究结果表明,本文提出的基于连杆机构的变弯度前缘优化设计方法能够实现柔性蒙皮的精确变形控制,具有较高的工程应用价值。但本文目前尚未涉及内部机构的详细优化设计,且蒙皮为无根梢比和无后掠的等直机翼模型。这两类因素都对最终的变弯度机翼工程应用有较大的影响,因此后续将针对此类问题开展进一步研究。

