考虑交叉口情况的公交专用道网络研究

顾悠扬，马晓旦，夏晓梅，叶静茹，李辰皓

（1.上海理工大学 管理学院，上海 200093；2.上海建科造价咨询有限公司，上海 200000）

1 引言

随着城市道路拥堵问题日益严重，如何提高现有交通网络效率已经成为交通专业人员面临的重要问题。虽然已有增加道路建设、扩大路网容量等措施，但现实发展表明，仅靠增加道路通行能力无法应对交通需求的持续增长。因此，实施公交优先策略成为建立高效交通系统的新方向[1]。实施公交优先，首先要保证通行权优先。在路网中布设公交专用道是保证通行权优先的一条有效途径。20世纪30年代，公交专用道的概念首次引入；1960年，法国率先通过设置公交专用道的方式来缓解交通拥堵，并提出“公交优先”[2]；1997年，国内第一条公交专用道布设于北京长安街。到目前为止，专家和学者们关于公交专用道的系统研究越发深入，可将研究分为微观与宏观两部分。

微观方面的研究，主要是对公交专用道的几何设计和相应的公交优先信号进行了详细的讨论。在几何设计方面，公交专用道可以是中心公交车道、偏置公交车道、路边公交车道和反向公交车道[3]，其设置通常是因地制宜、相当灵活。除了几何设计，适当调整的信号相位也被认为不可缺少。对于设置在路段中央的公交专用道，为了避免左转车辆与专用道上行驶的公交车辆的冲突，Kim提出了一种协调非公交阶段与专用公交阶段的三环相位方案，通过将剩余时间分配给公交专用道中位数通道上的非公交阶段，提高公交车辆的平均行驶速度和非公交车辆的通过率[4]。而从宏观方面来看，公交专用道的具体布设是研究重点。SEO等认为当公交车流量在20veh/h-400veh/h之间，车辆流量在1 730veh/h到3 350veh/h之间时，设置公交专用道[5]。Horimoto认为在主干道上设置公交专用道需证明其合理性，即当存在公交专用道时的行程时间小于无公交专用道的行程时间时，可设置公交专用道[6]。

本文提出以总出行时间最小为目标的模型，模型将车道分配和信号相位优化结合为一体，以此选择最合适的公交专用道网络设计。

2 公交专用道网络优化

公交专用道的网络优化问题是城市交通网络设计问题。随着数学设计和网络设计问题的发展，双层规划模型出现在大众视野，上层优化网络，下层从出行者的角度描述。Mesbah等提出了双层规划模型，以系统总出行时间为上层优化目标，下层为静态交通流量分配模型，求解公交专用道的最优布设[7]。Miandoabchi等提出了一个多目标双峰城市交通网络设计问题，包括小汽车和公交车模型以及道路网络和公交网络的同时设计，并考虑了两种模式的流量对彼此的影响[8]。针对公交专用道对路网运行效率的影响，考虑模型选择与公交专用道分配的相关性，Abdelghany等提出了一种动态交通分配和仿真模型，用于评估BRT不同运行特性对客运量和交通流的潜在影响[9]。Uchida等探讨了一个考虑出行者行为的网络设计问题，该问题由基于概率的多式联运分配模型表示，同时考虑了铁路、公交和小汽车三种交通方式，以及小汽车和公交车过饱和的相互作用[10]。

研究表明，公交专用道有助于改善路网运营状况，但无限制增加公交专用道并不可行。目前的公交专用道网络优化研究主要集中于专用道对路网整体的作用，而忽略了专用道在交叉口产生的影响。事实上，大多数交通延误都发生在交叉口。由于公交专用道的设置，其他车道在交叉口的减少可能导致绿灯时间的调整。因此，不仅相应路段上的车辆行驶会受到影响，相邻路段也会受到影响。忽略这种影响可能会低估公交专用道对网络的负面影响，导致网络优化设计结果不理想。

为了克服这一不足，本文提出的优化模型是通过选择最合适的公交专用道网络设计来减少总出行时间，即以系统出行时间最小为目标，将交叉口处的车道重新分配和信号相位优化集成在一个框架内。

3 模型建立

公交专用道的优化设计问题是一个复杂的决策问题，需要在路网系统中综合权衡决策者及出行者双方的利益。其中，决策者是关于公交专用道优化设计的决策部门，权衡的是整个网络系统的效益；而出行者更加关注的是自身的实际出行时间。因此采用双层规划模型。上层模型从系统角度出发，决定哪条路段上建设专用道、交叉口处公交专用道的设置以及形式为路中型还是路侧型，建立上层模型的目标函数，其优化结果保证整个路网系统的总出行时间最短；下层模型从小汽车和公交车两个角度来建立模型，在由上层模型确定出的包含铺设公交专用道的基础，出行者选择相应的出行路径来实现出行时间最少。

3.1 上层模型

上层模型以总出行时间最小为目标来建立目标函数，并给出了相应的约束条件，具体如下：

式中，VaC是路段a上的小汽车流量（人/h）；taC是路段a上的小汽车的阻抗函数（min）；VaB是路段a上的公交车流量（人/h）；taB是路段a上的公交车的阻抗函数（min）；Vriw是交叉口r上岔口i流向w的流量（人/h）；triw是交叉口r上岔口i流向w的阻抗函数（min）。

（1）路段车道功能划分约束条件。双向各功能车道数（公交专用道与社会车道）之和应与路段总车道数相等；同时，双向至少应有一条社会车道。

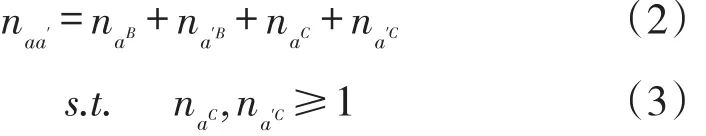
（2）交叉口车道功能约束条件。交叉口属于比较复杂的部分，约束条件也比路段更加多，在此引入进口和出口的概念。主要约束条件如下：进口车道数与各功能车道的车道数之和相等。进口车道数与出口车道数之和等于岔口总车道数之和，且进口与出口车道数之和不小于路段车道数；为了让社会车辆有车道可以行驶，因此进口道和出口道的社会车辆的车道数应不小于1。本文设定十字形交叉口，岔口i=4。

式中，nie是岔口i的进口车道数（条）；niO是岔口i的出口车道数（条）；是岔口i进口的公交车道数（条）；是岔口i进口的小汽车的车道数（条）；ni是岔口i的总车道数（条）；是岔口i出口的小汽车的车道数（条）。

（3）公交专用道几何设置约束条件。交叉口处公交专用道应与路段一致。若路段公交专用道设置为路外侧型，则交叉口处的设置形式也是路外侧型。

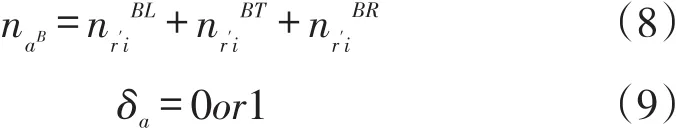
式中，naB是在路段处公交车的车道数（条）；是交叉口在岔口i处公交车左转的车道数（条）；T是交叉口在岔口i处公交车直行的车道数（条）；是交叉口在岔口i处公交车右转的车道数（条）；δa是公交专用道的形式，δa=0表示路中型，δa=1表示路侧型。

（4）交叉口信号控制。采用双环相位设计进行信号配时，图1给出了双环八相位的具体方向。

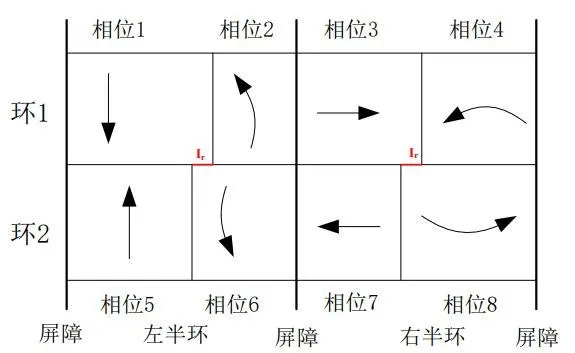
图1 双环八相位具体方向

式中，griw是流向w的绿灯开始时刻（s），其中w=1为左转，w=2为直行，w=3为右转；i=1,2,3,4分别为四个方向的岔口；Griw是流向w的绿灯时长（s）；Ir是交叉口 r的绿灯间隔时间（s）；C 是交叉口信号周期时长（s）。

（5）出行时间（阻抗）计算。本文采用BPR函数作为路段阻抗函数和交叉口阻抗函数，两者区别在于所取得参考系数不同。路段小汽车的阻抗函数记为taC，公交车的阻抗函数记为taB；交叉口阻抗函数记为triw。

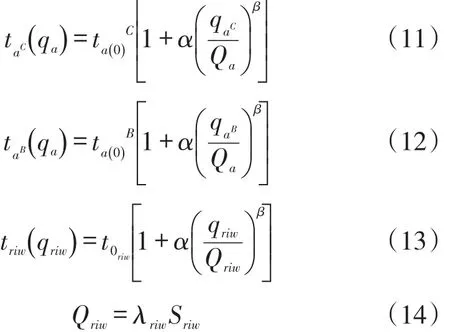
式中，qriw是交叉口r岔口i处w流向的流量（人/h）；Qriw是交叉口r岔口i处w流向的通行能力（人/h）；λriw是交叉口r岔口i处w流向的绿信比；是交叉口r岔口i处w流向的饱和流量是0流量时在交叉口r岔口i处w流向的行驶时间（min）；α，β是模型参数。

3.2 下层模型

下层分配模型采用随机用户均衡，分别对小汽车和公交车进行车流分配，即分为2个子模型，小汽车流量分配模型和公交车流量分配模型。

（1）小汽车流量分配模型。以广义出行时间最小为目标函数，以OD对及路段层次的流量守恒限制、容量限制及为保证路径流量为非负的可行解作为模型约束条件，公式如下：

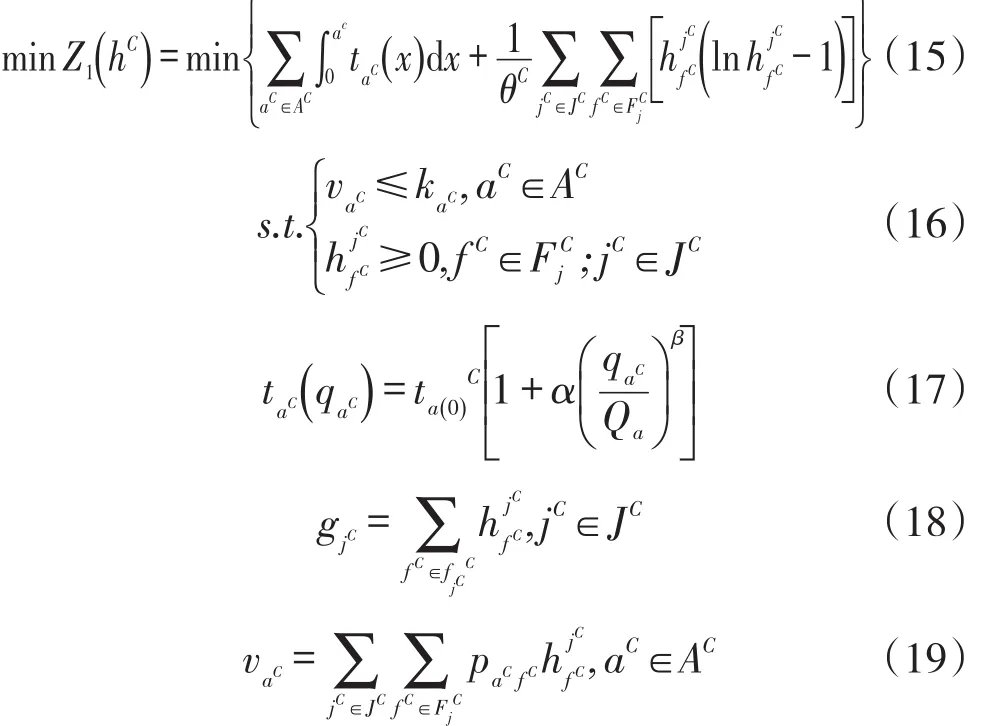
式中，ZC是小汽车网络广义出行费用（min）；AC是小汽车网络所有小汽车路段aC的集合；vaC是小汽车路段aC的乘客数（人）；taC是小汽车路段aC阻抗，即小汽车出行广义费用（min）；是乘客对小汽车网络熟悉度的量度，值越大表示对网络越熟悉，当θC→∞时，模型转换为用户平衡模型；为小汽车OD对的集合；是小汽车OD对之间所有的可行路径；fC是小汽车路径是路径上的流量是流量为时小汽车在路段a上的行程时间是零流量时小汽车在路段a上的行程时间（min）；Qa是路段a的可能通行能力（人/h）；α，β是模型参数是OD对之间的小汽车需求（人/h）；paCfC是0-1标记变量，若为1则表示路段aC在路径上，否则表示不在是路段aC的容量。

（2）公交车流分配模型。采用最优出行策略的分配方法对已知的公交流量进行路径分配，从而实现公交出行者的总出行时间最短。公式如下：

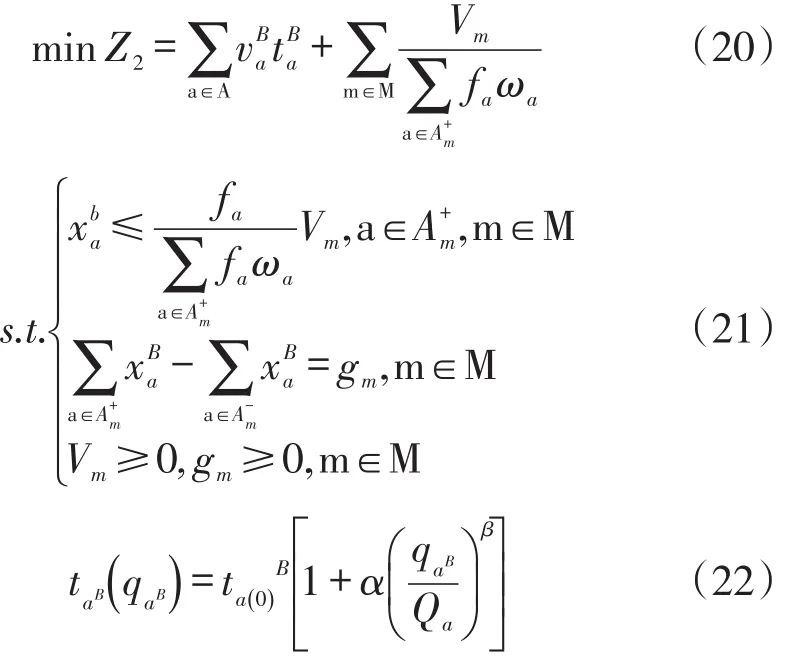
式中，Z2是公交网络广义出行费用（人/min）；m是公交网络中的节点；M是公交网络的节点集；A+m是进入节点m的线路集合；是离开节点m的线路集合；fa是路段a上通过的所有公交线路频率之和；ωa是0-1变量，表示路段a是否属于集合；gm是节点m上产生的客流量；是流量为时公交在路段a上的行程时间（人/min）是零流量时公交在路段a上的行程时间（人/min）；Qa是路段a的可能通行能力（人/h）；Vm是节点m上的客流量；α，β是模型参数。

3.3 模型求解

在模型求解方面，由于遗传算法同时具备随机性、自适应性、收敛性及与其它算法的兼容性等特性，适合求解网络优化问题，本文采用遗传算法求解上层模型，得到公交专用道的布局。下层模型则通过交通规划软件EMME中的公交分配模块及小汽车分配模块实现。

遗传算法具体步骤如下：

步骤1：设置进化代数计数器t=0，设置最大进化数T，随机生成M个个体作为初始群体P(0)。

步骤2：计算群体P(t)中每个个体的适应度。

步骤3：将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。

步骤4：将交叉算子作用于群体。

步骤5：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算后得到下一代群体P(t+1)。

步骤6：若t=T,则输出最优解，终止计算。

通过上层得到的专用道优化布局，下层利用交通规划软件EMME来解决网络流量分配问题。在EMME中，通过模式选择将公交专用道和其他车道设置为不同的路段，以此区分通行车辆的种类。因此，交叉口所有可能出现的交通流，最初应该由16个节点和40个链路来表示，经过道路简化后，改为使用16个节点和24条链路，相比之下减少了40%的链路。

4 验证与分析

4.1 路网参数标定

路网有3条公交线路，3个十字交叉口。公交线路1和2的需求量都为30pcu/h，公交线路3的需求量为10pcu/h。小汽车的OD对（4，8）、（8，4）、（3，11）、（11，3）交通需求量为200pcu/h，其余的OD对的交通需求量为50pcu/h。设定迭代长度为120s；任何一对相冲突的岔口的时间间隔设定值为4s；在交叉点处的所有车道的饱和流量均设置为1 800pcu/h；在路段与岔口处的自由流行程时间分别为10s和20s；公交车的乘客数设定为50人/辆，小汽车的乘客数设定为2人/辆；在BPR函数中，路段上的α取值为1.5，β取值为2；岔口上的α取值为2，β取值为3。

4.2 验证分析

为了更好地说明情况，本文选取东西向路段的公交专用道全部为路外侧型。为了论证交叉口对路网的影响，根据模型可将公交专用道的布局设置为三种进行对比分析，分为考虑交叉口和不考虑交叉口情形下进行，如图2-图4所示。

图2、图3、图4分别对应方案一、方案二、方案三，对比结果见表1。

图2 路网示意图

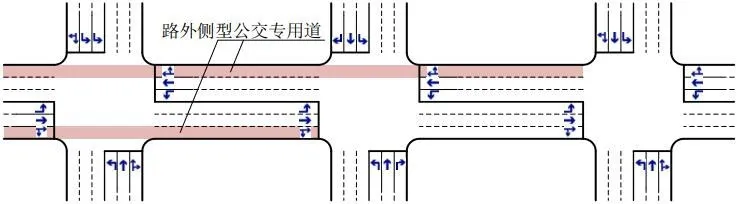
图3 考虑交叉口的公交专用道优化布局

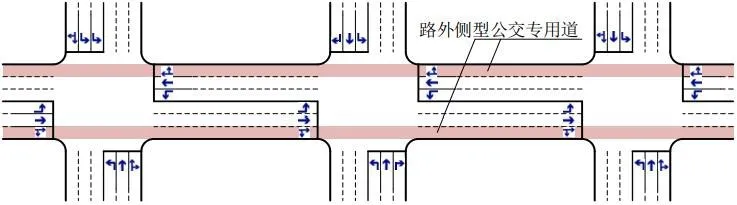
图4 不考虑交叉口的公交专用道优化布局

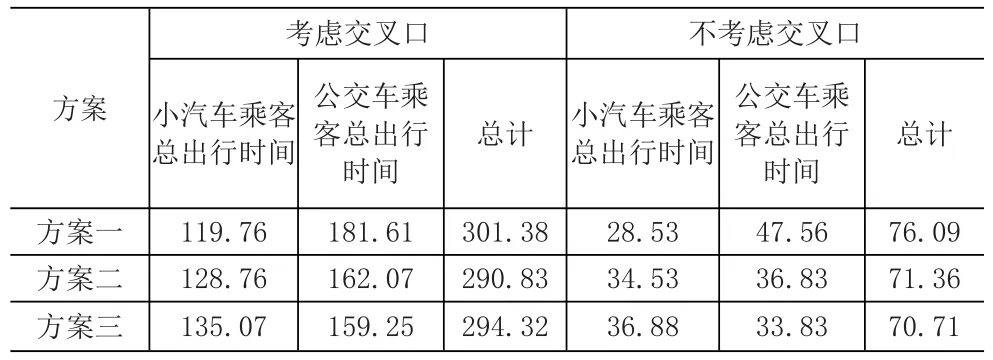
表1 两种情形下的乘客总出行时间（h）

由表1可知，在考虑交叉口的情形下，方案二是最佳方案；而在不考虑交叉口的情形下，方案三是最佳方案。相比之下可以看出，若忽略交叉口，会造成错选最优方案；而考虑交叉口情形下的出行时间总体远大于不考虑交叉口的情形，证明了交叉口是造成延误的重要因素。

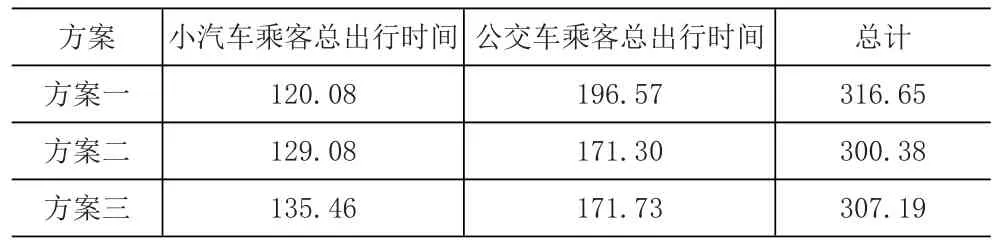
表2 当公交线路3的交通量为30pcu/h的对比

表2是为了论证公交专用道设置是否越多越好，将公交线路3的公交车的需求量增加至30pcu/h。由结果可知，方案二的总出行时间最少，是最佳方案。对比公交车乘客总出行时间，方案二略低于方案三，这表明公交专用道设置增多的情况下，随着路网中公交车的交通量增加，公交车出行时间差距并不大；将小汽车总出行时间进行比较，可以看出方案三的总出行时间最大。因此，当路网中公交车流量增加时，过多设置公交专用道会占用原有车道，造成小汽车延误增加，交叉口的通行效率降低，即使公交车在路段行驶时间减少但在交叉口的行驶时间可能反而增加。

5 结语

本文为减少总出行时间，提出了公交专用道网络设计的双层优化模型。基于建立的双层规划模型，提出采用遗传算法求解上层模型，下层采用EMME软件中的公交分配模型及小汽车分配模型进行求解。对模型进行验证，通过不同方案的比较，得出以下结论：

（1）本文基于网络优化，提出了基于系统最优与出行者最优的双层规划模型，将系统人均总出行时间最少作为上层模型的目标函数，并给出相关的约束条件；在下层模型中，以人均总出行时间最少为目标，采用随机配流分配模型，包括公交车及小汽车的分配模型。该模型考虑了公交专用道与公交车辆在交叉口的相互作用，优化了公交专用道的布局，避免产生错选最优方案的后果；

（2）实验证明，本文建立的模型减少了所有乘客的总出行时间和小汽车乘客的出行时间。这表明，公交专用道设置的不合理可能会对小汽车出行造成负面影响。