考虑碳排放的煤炭铁海联运路径优化

陈红梅,宋浩贤,田 然

（燕山大学，河北 秦皇岛 066000）

1 引言

随着环境污染的日益加剧和可持续发展的要求，全球对“低碳化”的关注度越来越高，许多国家已经开始对碳排放实施碳税政策。作为碳排放大国，我国承诺到2020年单位国内生产总值二氧化碳排放量相比2005年降低40%-45%，“低碳化”已成为我国经济发展的必然趋势。作为我国重要的战略能源，煤炭在运输途中消耗能源的同时，也会产生大量的碳排放，因此，实现煤炭的“低碳化”运输对发展低碳经济具有重要意义。由于我国煤炭产地与消费地相距较远，单一的运输方式难以满足最优化运输的要求，因此需要多种运输方式的组合（即多式联运）。研究表明，铁海联运是最适合煤炭的运输组织方式，较单一运输方式，铁海联运最多可减少77.4%的碳排放和43.48%的燃油，大力发展铁海联运可以有效减少煤炭运输中的碳排放，缓解煤炭物流对环境的污染[1]。

国内外学者对多式联运进行了富有成效的研究。Wang等建立考虑物流资源计划（LRP）和多模态的多式联运路径优化模型，并通过GAMS软件和CPLEX求解器求解[2]。Saeed等综合考虑了多式联运节点选址和路径优化问题，以成本最小建立优化模型，并设计相应的遗传算法求解，该算法能有效解决GAMS和CPLEX求解器无法在合理时间内找到最优解的问题[3]。Xiong等基于图论建立了考虑运输时间和成本的多式联运双层路径寻优模型，并设计了相应的多目标Taguchi算法来寻找帕累托最优解[4]。生鲜货物较一般货物具有较强的特殊性，对运输的要求也更高，Pawel等从货物安全最大化和运输成本最小化角度研究了易腐生鲜商品的运输路径优化问题[5]。考虑到多式联运中的拥塞效应，Sushil等建立了考虑拥塞效应的两阶段路径规划模型，通过嵌套分解算法和PH算法求解[6]。在考虑碳排放的多式联运中，Cecília等建立了考虑碳排放的多模态单程TRIPS优化模型，并采用经典的标量化方法进行求解[7]。Lam等通过建立以运输成本和时间为目标、碳排放为约束的优化模型，研究了碳排放约束下的多式联运路径优化问题[8]。Gocmen等建立了考虑社会风险和生态风险的路径优化模型，设计改进后的模糊算法对模型求解[9]。在煤炭铁海联运的研究中，蔡文结合我国煤炭调运实际情况与铁海联运特征，建立了基于成本最小的煤炭调运模型，并通过Lingo软件进行求解[10]。田怀秀通过构建多商品流模型研究了铁海联运下的煤炭路径优化问题[11]。

现有研究多从运输时间、成本等方面考虑多式联运路径优化问题[12-16]，较少考虑碳排放因素，一些学者虽然将碳排放加入优化目标中，但多为建立多目标优化模型，将碳排放作为其中一个优化目标，未能有效评估碳排放的经济成本[17-18]。此外当前研究多集中于集装箱领域，关于煤炭等大宗散货的研究相对较少。因此，本文通过引入碳税机制，构建以运输成本和碳排放成本最小为目标的铁海联运路径优化模型，研究了碳税机制下的煤炭铁海联运路径优化问题。

2 问题描述与建模

2.1 问题描述

煤炭铁海联运过程如下：供应商根据客户需求，委托铁海联运经营人将煤炭由产地发运至需求地，期间首先将矿区生产的煤炭汇聚到集货点集货，然后通过铁路将煤炭运送至下水港，在下水港中转换装后由海运发运至上水港，上水后配送至客户手中。在煤炭铁海联运网络中，各运输弧段与节点都存在运能约束。成本包括运输成本和碳排放成本两部分，其中运输成本主要包括各运输弧段的运输费用、节点的中转换装费用、港口的作业费用以及堆场的堆存费用；碳排放成本为在征收交通运输业碳税的背景下，煤炭运输途中和转运时产生的碳排放所需缴纳的碳税金额。对铁海联运经营人而言，需要决策的问题是：如何安排运输路径，使得整个铁海联运网络的总成本最小。

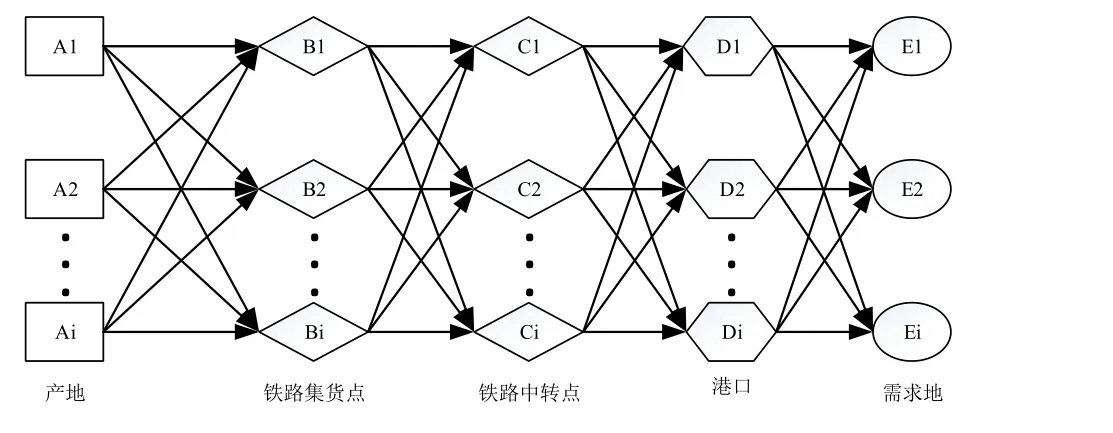
图1 煤炭铁海联运概念图

上述问题可归类为网络配流问题，不仅需要考虑运输网络的路径规划问题，还需要考虑运输网络中各线路的配流问题。针对上述问题，建立煤炭铁海联运路径优化的多商品流模型，该模型将每一股不同的货物流视为一种商品，根据多股货物流在运输网络上的空间叠加特征进行建模，从而寻找最优的运输路径。

2.2 符号和变量

Nv：煤炭产地集合，v={1,2...,V}；

Nw：铁路节点集合，w={1,2...,W}

Ns：港口节点集合，s={1,2...,S}；

Ne：煤炭消费地集合，e={1,2...,E}；

Pi：产地i的煤炭产能，i∈Nv；

Yj：消费地j的煤炭需求量，j∈Ne；

Qij：节点 i到 v通道的运能约束，i∈Nv⋃Nw,j∈Nw⋃Ns；

Qi：节点i的转运能力约束，i∈Ns；

Cij：节点 i到 j的单位运输成本（元/t·km），i∈Nv⋃Nw⋃Ns,j∈Nw⋃Ns⋃Ne；

Cs：港口单位中转成本（元/t）；

Cp：港口单位堆存成本（元/t）；

Hi：港口最大煤炭吞吐量（t），i∈Ns；

T：煤炭在港平均堆存时间；

Cz：交通运输业碳税税率（元/kg）；

dij：节点i到j运输里程（km），i∈Nv⋃Nw⋃Ns,j∈Nw⋃Ns⋃Ne；

F1：铁路运输单位碳排放量（kg/t·km）；

F2：水路运输单位碳排放量（kg/t·km）；

F3：港口中转作业单位碳排放量（kg/t）；

（2）决策变量

xij：节点 i到 j的煤炭运量，i∈Nv⋃Nw⋃Ns,j∈Nw⋃Ns⋃Ne。

2.3 模型构建

2.3.1 模型假设

（1）交通运输业所征收的单位碳税是已知的。

（2）网络中各运输弧段运能不得超过能力限制，且各运输弧段的运能均为已知。

（3）煤炭的中转换装只能发生在节点城市处。

（4）煤炭在节点处可拆分成多股分别运输，将每一股不同的煤炭流视为一种不同的商品。

（5）在运输过程中，煤炭质量不会增加或减少，不考虑随机事件等因素的干扰。

（6）将上水港视为煤炭需求地，总成本中不考虑上水港作业费用。

2.3.2 模型建立

根据符号说明和模型假设建立考虑碳排放的铁海联运路径优化模型：

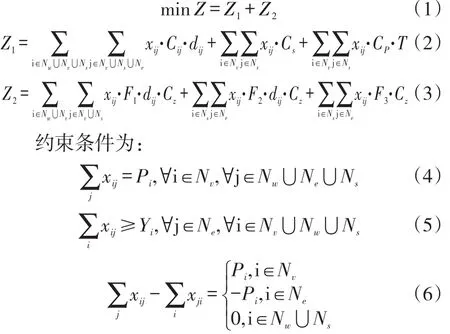
式（1）由运输成本和碳排放成本组成，表示整个网络总成本Z最小；式（2）由节点间的运输成本、中转成本和堆存成本三部分构成，表示整个网络的运输成本；式（3）由节点间运输、中转产生的碳排放成本构成，表示整个目标网络的碳排放成本；式（4）表示煤炭产地流量守恒约束；式（5）表示运输至消费地的煤炭数量满足需求；式（6）表示网络中各节点间流量守恒约束；式（7）表示铁路运输通道运能约束；式（8）表示港口煤炭吞吐能力约束；式（9）为决策变量非负约束。

3 求解算法

遗传算法采用遗传机制不断更新种群，具有较强的健壮性和全局搜索能力，但传统遗传算法的进化速度较慢，容易收敛到局部最优解，同时当问题复杂时，算法耗时较长。因此，在遗传算法的基础上引入精英保留策略，对算法进行改进，设计改进后的算法对模型求解，改进后算法求解步骤如下：

（1）染色体编码。采用单层染色体自然数编码方式，编码时，用“0”（产地）作为染色体的头部，如“0，2，6，8”，此染色体表示煤炭从产地0出发，依次经过节点2、6，最后到达需求地8。

（2）种群初始化。随机产生个体数为N的种群P0，设定最大遗传代数T，交叉概率Pr，变异概率Pm。

（3）适应度值评估。根据模型中的目标函数对种群中的染色体进行排序，得出其所属的Pareto前沿等级。

（4）选择操作。采用轮盘赌选择策略，对于规模为n的群体P={a1,a2，…,an}，个体aj的适应度值为f(aj)，则其选择概率为：

（5）交叉、变异操作。交叉采用正态分布策略，变异采用改进的自适应调整变异方式。

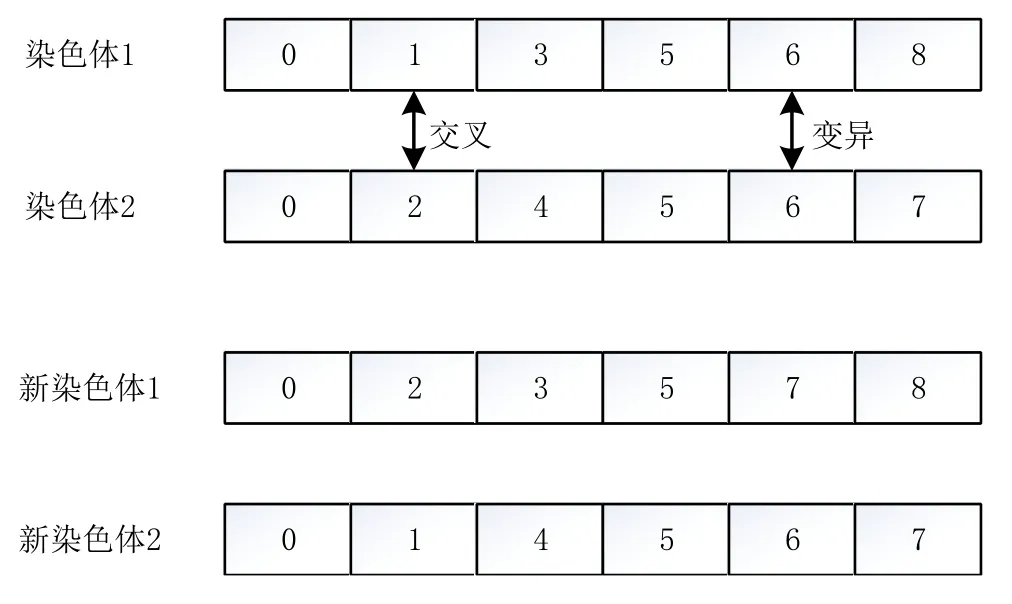
图2 染色体交叉变异示意图

（6）精英保留策略。在进化过程中，把每代的优秀个体保留下来作为下一代的父代，降低计算复杂度，加快算法的全局收敛速度，同时保证精英个体不被遗漏。

（7）终止条件。若运行代数达到最大遗传代数T时，终止运行，否则转到步骤（3）。

（8）得到目标函数的Pareto最优解集。

改进后的遗传算法流程如图3所示。

4 算例分析

4.1 背景设计

图3 改进后的遗传算法流程

以鄂尔多斯煤炭调运为例进行分析，2018年鄂尔多斯市煤炭产量为6.16亿t，居全国第一位。假设鄂尔多斯市每年有3.5亿t煤炭需要通过铁海联运运输至广州、上海、宁波、福州，四地煤炭需求量分别为1亿t、1亿t、1亿t、0.5亿t。下水港为北方煤炭港口中的秦皇岛港、唐山港、天津港和黄骅港。运输网络如图4所示，要求在该运输网络内，选择最优的运输路径。为方便对各节点进行编号：鄂尔多斯为A1；准格尔、神木、呼和浩特、大同、朔州、集宁和迁安依次为B1-B7；秦皇岛港、唐山港、天津港、黄骅港依次为C1-C4；广州、上海、宁波、福州依次为D1-D4。

图4 鄂尔多斯煤炭铁海联运网络图

铁路运输通道运距及运能见表1。由于铁路煤炭运费计价方式不尽相同，为了方便研究，本文选取国铁煤炭运费计价进行分析。国铁整车煤炭运输费用由基价1、基价2和铁路建设基金组成，其中基价1为16.3元/t，基价2为0.098元/t·km，铁路建设基金为0.033元/t·km，国铁煤炭运价计算公式为Ct=TJ+J1*d+J2*d，TJ—基价1(元/t)；J1—基价2(元/t)；J2—铁路建设基金(元/t·km)。

参考秦皇岛港、唐山港、黄骅港和天津港煤炭年设计通过能力与近年吞吐量数据，本文假设津冀四港煤炭最大年吞吐能力为：秦皇岛港2亿t、唐山港3亿t，天津港1亿t，黄骅港2亿t。由于海运价格受季节波动较大，且随船型和距离不同而存在差异，因此本文将4-5万DWT海运价格平均值作为各港口间的单位海运费用，港口间海运里程及单价见表2，该数据参考自中华航运网和中国煤炭信息网。我国北方煤炭港煤炭装船费用为20-30元/t，煤炭的搬运、分拣等中转费用约18-28元/t，因此设定煤炭中转费用总和为50元/t。煤炭在港口内堆存时间取北方煤炭港口平均堆存时间，设定为6d，港口堆存费取0.2 元/(t·d）[19]。

征收碳税已经被证明是最具成本效益的碳减排手段之一，目前部分国家已经开始征收碳税，英国规定各行业每吨碳排放征收6.28英镑；日本对消费化石燃料的企业，每吨碳排放征收655日元；荷兰对一定经济范围内的企业每吨碳排放征收21欧元。结合国外碳税征收情况与国内相关研究，假设我国未来征收碳税成本Cz=0.1元/kg。设定煤炭铁路运输单位碳排放为0.022（kg/t·km)、水路运输单位碳排放为0.016（kg/t·km）、铁水中转单位碳排放为4.28（kg/t）[11]。

4.2 结果分析

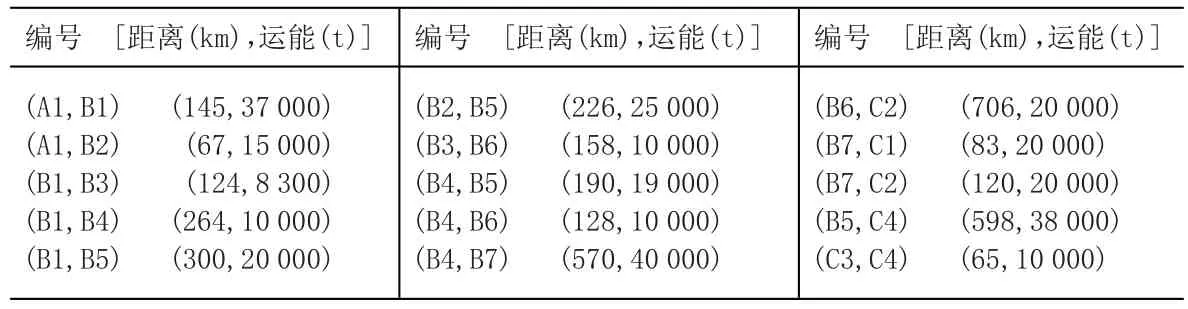
表1 运输通道运距及通过能力

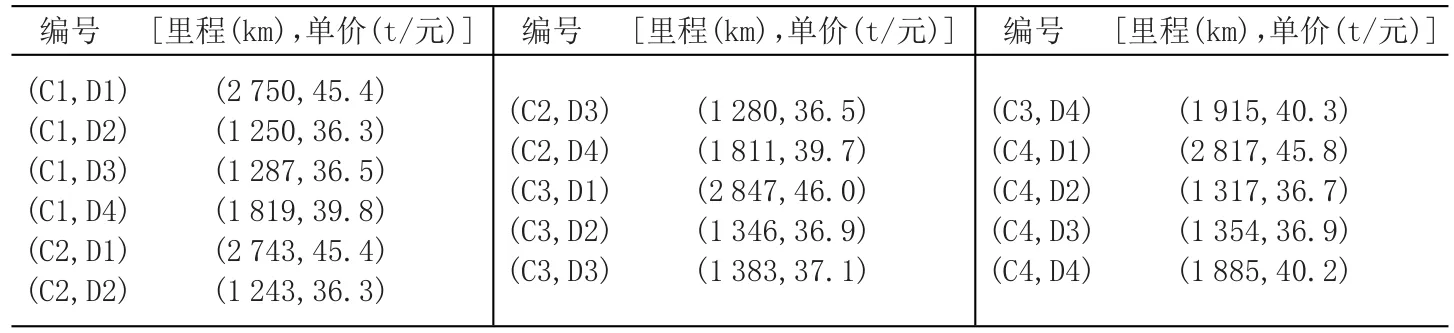
表2 海运里程及单价

采用MATLAB对该路径进行模拟仿真。进行实验的计算机配置为英特尔(R)酷睿(TM).i5-4210U2.7GHzCPU,2.0内存。设定种群规模为100，最大遗传代数300，变异概率0.01，交叉概率0.9。

得到最优化的调运方案见表3。

即3.5亿t煤炭拆分成五部分进行运输，第一部分1.5亿t煤炭经包神线由鄂尔多斯运输至神木，再经神朔线运输至朔州，由朔州运输至黄骅港进行下水，最后1亿t煤炭经水路发运至广州，0.5亿t煤炭经水路发运至宁波；第二部分1亿t煤炭经巴准/准东线由鄂尔多斯运输至准格尔，再经大准线运输至大同，由大同经大秦线运输至秦皇岛港进行下水，0.7亿t煤炭经水路发送至上海，0.3亿t煤炭经水路发运至宁波；第三部分0.5亿t煤炭经巴准/准东线由鄂尔多斯运输至准格尔，再经准朔线运输至朔州，由朔州运输至黄骅港进行下水，最后经水路发运至宁波；第四部分0.2亿t煤炭经巴准/准东线由鄂尔多斯运输至准格尔，再经准朔线、北同蒲线中转至大同，由大同运输至秦皇岛港进行下水，最后经水路发运至宁波；第五部分0.3亿t煤炭经巴准/准东线由鄂尔多斯运输至准格尔，再经呼准线、京包线运输至集宁，由集宁运输至唐山港进行下水，最后经水路发运至上海。最优化方案的目标函数值为843.05亿元，运输过程中碳排放总量为0.192 5亿t。

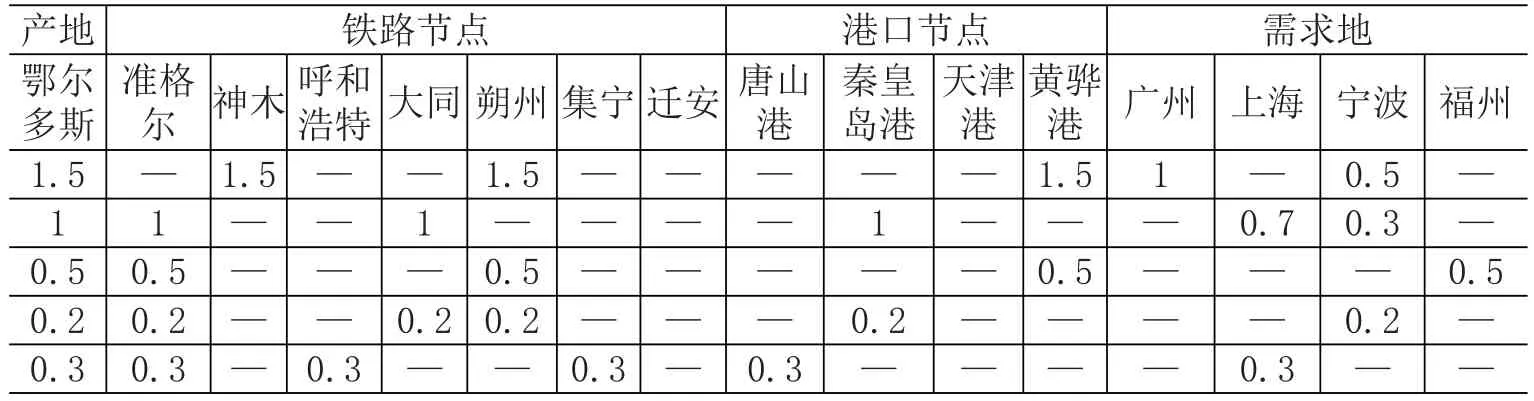
表3 煤炭调运优化计算结果 (亿t）

5 结论

在国家大力倡导“低碳化”经济发展的背景下，本文研究了考虑碳排放的煤炭铁海联运路径优化问题。在结合煤炭铁海联运实际情况的基础上，通过引入碳税机制，构建了相应的路径优化多商品流模型，使得在煤炭运输过程中同时考虑运输成本和碳排放成本，从而引导煤炭铁海联运经营人选择碳排放水平较低的路线进行运输。在求解算法方面，设计了一种带精英策略的遗传算法，通过引进精英策略，使得优良的种群个体在迭代过程得以保留下来，从而提高了优化结果的精度和算法求解速度。最后以鄂尔多斯地区煤炭调运为例验证了模型和算法的有效性。

由于煤炭等能源类货物较一般货物具有较强的特殊性，在今后的研究中，需要进一步研究能源类货物运输中碳税等参数的选择，继续探讨碳税成本对煤炭铁海联运路径优化的影响，使得研究结果更加符合我国的实际国情。