弧形折纸模式薄壁结构的压缩变形与能量吸收*

张天辉，邓健强，刘志芳，李世强

（太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024）

薄壁结构作为吸能装置被广泛应用于吸能缓冲、抗冲击领域，近年来，折纸图案在管状薄壁结构上的应用越来越受到关注[1]。研究发现，如果在管件表面预制不同模式的折痕，可调控在轴向外力作用下结构的屈曲模式和能量吸收性能。在圆管表面引入波纹，可以产生较低的初始峰值力和更均匀的压缩过程[2]。Zhang 等[3]通过数值模拟研究了两种具有金字塔形状的方形管，发现其能量吸收比传统方管分别提高了(15～33)%和(54～93)%。Zhao 等[4]在折纸管中引入具有有限厚度和长度的铰链区域，并利用3D 打印技术进行设计，这种设计充分展示了3D 打印技术为增强折纸结构的承载能力和可控的变形模式提供了设计灵活性与制造效率。Ma 等[5]提出了一种新的装置，该装置是根据一种特别设计的折纸图案，在方形管的表面预折而成。和传统方管相比，在该设计中，初始峰值力降低了20%以上，能量吸收增加了50%以上。Song 等[6]应用了一种折纸图案做成方形管，使初始峰值力最小化。Zhou 等[7]提出一种梯形折纸薄壁结构，其表面根据可展开的折纸图案预先折叠，并在方管表面引入一种梯形折痕以降低峰值力，将设计中最优的梯形折纸管与传统的等质量方管和八边形管比较，发现梯形折纸薄壁结构在吸能方面优于传统薄壁结构。周昳鸣等[8]针对这种折纹管进行了优化设计。郝文乾等[9]采用LS-DYNA 软件研究了6 种折纹管在轴向冲击载荷下的屈曲模式和能量吸收性能，发现折痕的引入有效地降低了初始峰值力，并且部分折纹管的压缩力效率和比总体效率高于方管的。Hou 等[10]和Ma 等[11]基于风筝形折纸模型，提出了一种截面为风筝形的管状结构，与传统方管相比，其峰值载荷降低了67.2%，能量吸收提升了36%。与传统的方形管相比，在保证能量吸收能力一定的情况下，具有初始折痕的薄壁管具有较低的初始峰值力和更均匀的压缩载荷。

本文中，将折纸艺术与3D 打印技术相结合，设计并制备了面外方向具有初始折叠角度的弧形折纸薄壁管件单胞及其阵列结构，基于准静态轴向压缩实验，利用ABAQUS 对弧形折痕薄壁管件在轴向压缩下的力学行为和吸能特性进行了数值模拟分析，探讨了结构的变形模式，分析了预折角的大小、单胞、面内阵列个数以及不同的冲击速度对其压缩行为的影响。由于压缩行程、质量是吸能结构设计与评价的主要参量，所以本文中将高度相等、质量近似相等（结构最大质量差为0.07 g，最小质量差为0.01 g）的方管及其阵列结构进行对比，发现弧形折痕的引入能够有效地降低初始压溃载荷峰值并减小冲击载荷作用下冲击力位移曲线的振荡幅值，可以作为一种变形可控的吸能结构。

1 几何模型

本文中所研究的模型主要由一个矩形薄板沿着预定的折痕折叠而成，如图1(a)所示。其中，DE 长度记为c，AD=DG=GK= h0，折痕倾角∠ABE 记为α，折痕BE=CF=HL=IM=a，可得：

将基本单元沿折痕BE、EH、HL 折叠成图1(b)所示的几何形状，其中，倾斜翼缘BCFE 和水平面的夹角β、腹板DEHG 和腹板FEHI 的夹角ξ 以及BE 与水平面的夹角θ 由以下几何关系进行计算：

因此，几何模型可根据c、a、α、ξ 来确定。为保证折纸管单胞的可周期阵列性，设计折痕时，令EF=2DE，OF=4DE，腹板DEHG 和腹板FEHI 的夹角ξ=60°。将2 个沿折痕折叠成的单元对称连接，得到弧形折纸薄壁管件，如图1(c)所示。长、宽、高分别用l、w、h 表示（图1 中弧形实折线（CFIM）为向外的峰线，弧形虚折线为向内的谷线），其中：

本文中所研究的模型均使用3D 打印机打印制造，在建立3D 打印模型时，连接面DEHG与其他竖直腹板的厚度一致。

图1 弧形折痕薄壁管建模过程Fig. 1 The modeling process of an origami thin-walled tube with the arc-shape pattern

2 实验研究

本研究中所有样品均采用Volunex Mars Plus+ 3D 打印机打印。使用的材料为PolyMaxTMPLA，成型后材料密度为1 200 kg/m3，泊松比为0.35，弹性模量为1.97 GPa。利用SHIMADZU AG-25TB/SFL-5AG 材料试验机，参照拉伸测试规范ASTM D638-10 测试了拉伸试样在准静态（应变率为10−4s−1）拉伸时的力学参数，初始屈服强度为40 MPa，断裂应变约为0.3。拉伸试样的几何参数及真应力应变曲线如图2(a)所示。

3D 打印试件力学性能与其打印工艺关系密切，对于熔融堆积法打印工艺，试件拉伸力学响应与打印角度相关性较大。本文研究的管状结构打印模式为沿着结构轴线向上铺层打印，为保证基体材料力学性能测试的可靠性，试件打印选取沿长度方向铺层打印，如图2(b)所示。

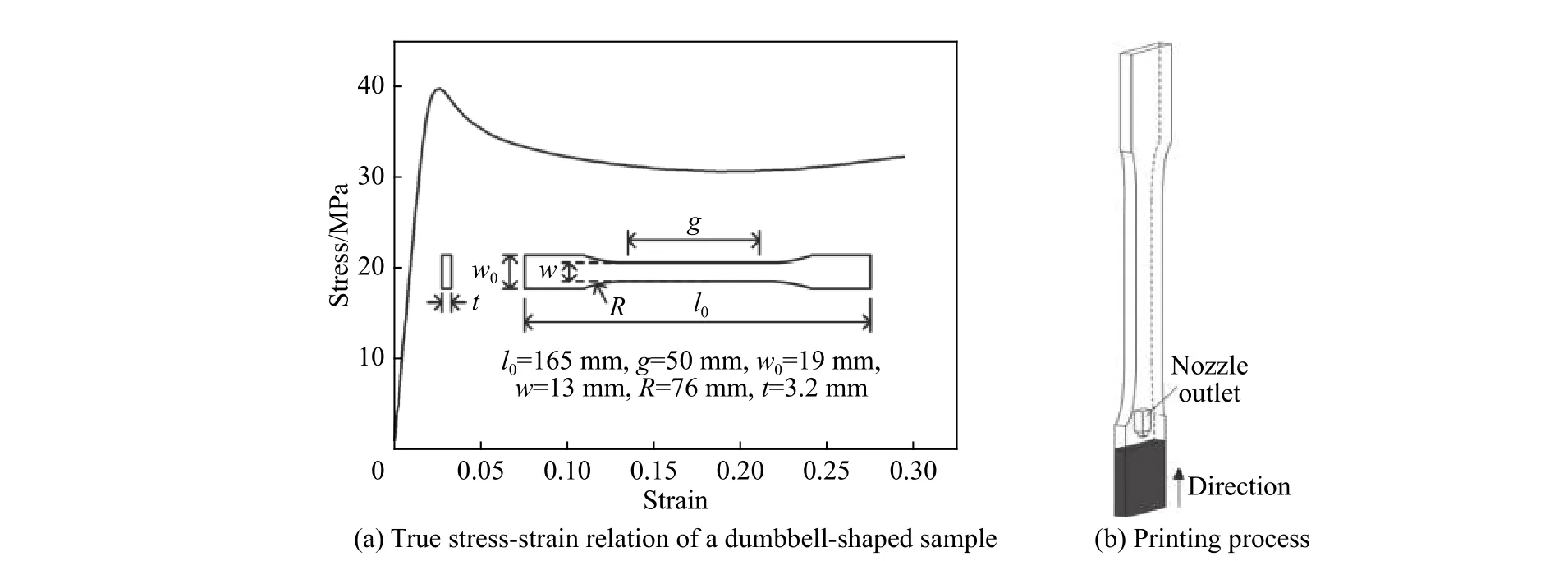
图2 利用PolyMaxTM PLA 打印的哑铃形试件的拉伸真实应力应变关系及打印工艺Fig. 2 True stress-strain relation of a dumbbell-shaped sample printed with PolyMaxTM PLA and the corresponding printing process

根据前文所述几何模型，利用Volunex Mars Plus+3D 打印机制造表观尺寸（l×w×h）为80 mm×80 mm×60 mm、预折角α=60°、壁厚τ=1 mm、在面内方向阵列个数n 为2×2 的薄壁管状结构，在ABAQUS 中建立了相应的有限元模型。实验中，采用SHIMADZU AG-25TB/SFL-5AG 压缩试验机，压缩速度为1 mm/min；压头为钢制平板，与结构自由接触。结构在准静态压缩载荷下的实验和数值模拟对比结果如图3 所示，两者吻合较好。数值模拟的模型尺寸与实验相同，有关单元类型、材料模型及接触关系的详细信息见第4 节。由于数值模拟中未考虑摩擦效应的影响，结构的压缩力略低于实验值。

图3 模拟与实验压缩载荷-位移曲线对比Fig. 3 Comparison of compressive load-displacement curves between simulation and experimentl

从图3 可以看出，结构变形可定性地分为4 个阶段。初始压溃阶段：当结构受到初始压缩载荷时，压缩力迅速上升至峰值载荷，约为7.5 kN。之后，结构进入预折角塑性旋转阶段：预折角开始发生塑性旋转变形，同时伴随有局部破坏，此时结构压缩力呈非线性下降趋势。随着预折角的进一步旋转，结构压缩力逐渐上升，当腹板两侧倾斜部分旋转至水平位置时，压缩力主要有腹板承担，在力-位移曲线上出现第2 个峰值载荷，约为10 kN，这个过程为腹板塑性屈曲阶段。当腹板受力发生屈曲后，压缩力下降，随后整个结构逐步进入压缩密实化阶段。

3 数值模拟

针对不同几何参数的弧形折纸模式薄壁结构开展准静态和动态压缩数值模拟。弧形折纸薄壁管单胞根据其预折角α 的不同取3 种，分别记为A50°、A60°、A70°，与之对比的方管记为SQU。由于常用的多孔夹芯抗冲击防护结构芯层厚度在15～40 mm 之间[12-13]，因此本节中所涉及的弧形折纸模式单胞结构（实验组）和方管单胞模型（对照组）的相关参数如表1 所示。

表1 模型参数Table 1 The parameters of the models

3.1 有限元模型及算法验证

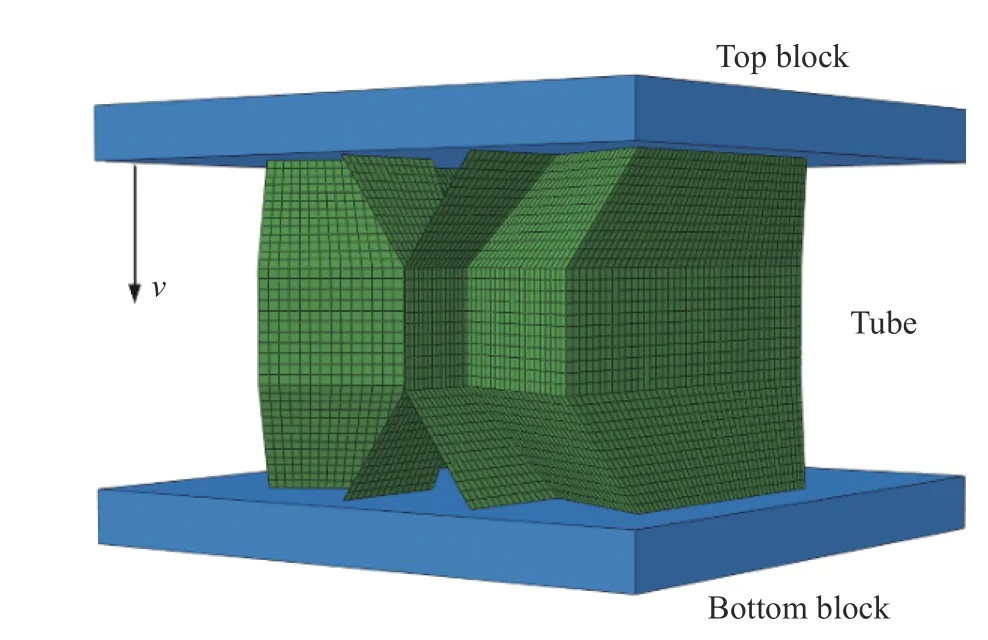
图4 弧形折痕薄壁管状结构单胞有限元模型Fig. 4 The finite element model of a curved origami thin-walled tube

结构单胞有限元模型如图4 所示，折纸管采用S4R 壳单元，上下板为刚体。对于2×2 阵列模型，在建模时直接把所有的单胞合并为一个整体。经过网格敏感性和有限元算法验证后（图5～6），数值模拟中的模型网格尺寸确定为1 mm，上下板和折纸管采用自接触，忽略摩擦的影响，上板采用1 m/s 的压缩速度来模拟准静态加载过程(总动能必须比压缩过程的总内能小得多，压缩力位移响应必须与所施加的速度无关[14-15])。

从图5 可以看出：折纸管在①处产生初始压溃应力峰值，随后进入预折角塑性旋转阶段（①～②），该阶段称为第1 平台段；预折角塑性旋转阶段结束后，应力值开始上升，此时主要承载部分为折纸管的竖直腹板，在折纸管出现第2 个压溃应力峰值（③）之后，折纸管进入腹板塑性屈曲阶段（③～④）该阶段称为第2 平台段；当竖直腹板完全压溃之后（④之后），整个模型进入密实化阶段。

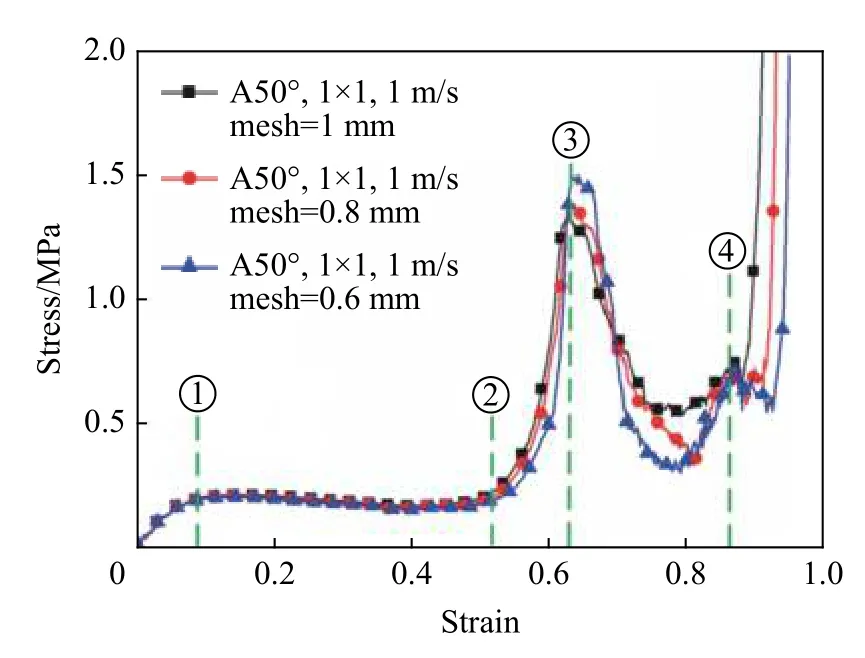
图5 网格敏感性验证Fig. 5 Validation of mesh sensitivity

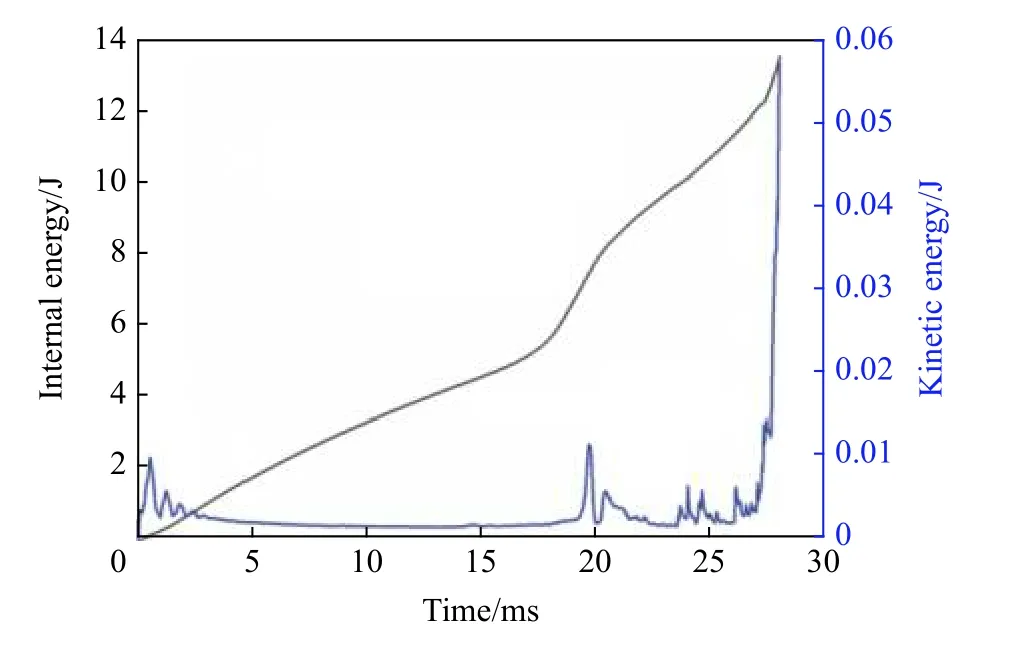
图6 有限元算法验证Fig. 6 Verification of the finite element algorithm

3.2 参数分析

3.2.1 预折角及面内方向阵列个数的影响

本文中所涉及的应力应变曲线均为名义应力-名义应变曲线。名义应力σ 为压板与薄壁管件接触面上的力与模型初始横截面面积之比，名义应变ε 定义为模型沿压缩方向的整体压缩与原长度之比，即：

式中：f 为压缩载荷，Δl 为压缩位移。

弧形折纸薄壁管和方管的单胞在准静态压缩作用下的应力-应变曲线如图7 所示。由图7 可知，随着预折角α 的增大，折纸管在初始压溃应力峰值越大，折纸管的第一平台段应力应变曲线的变化趋势一致且应力值的大小基本保持恒定，在ε=0.62 时，模型的主要承载部分由预折部分变为竖直的方管，折纸管产生第2 个应力峰值，进入腹板塑性屈曲阶段。由于竖直管部分发生坍塌失效后，模型失去承载能力，折纸管的应力应变曲线会出现下降趋势。在此过程中，A50°单胞模型发生整体坍塌，模型承载能力急剧下降；A60°、A70°单胞模型产生渐进压溃模式，在压缩过程中，每个竖直板发生坍塌失效都会对应产生一个峰值应力，因此，A60°、A70°单胞模型的应力应变曲线会发生波动。方管的单胞模型在模拟中的初始压溃应力峰值最大。与只具有一个平台阶段的方管相比较，折纸管的第1 平台段应力值与方管平台阶段的应力值相近，折纸管的第2 平台段应力值高于方管平台阶段的应力值。

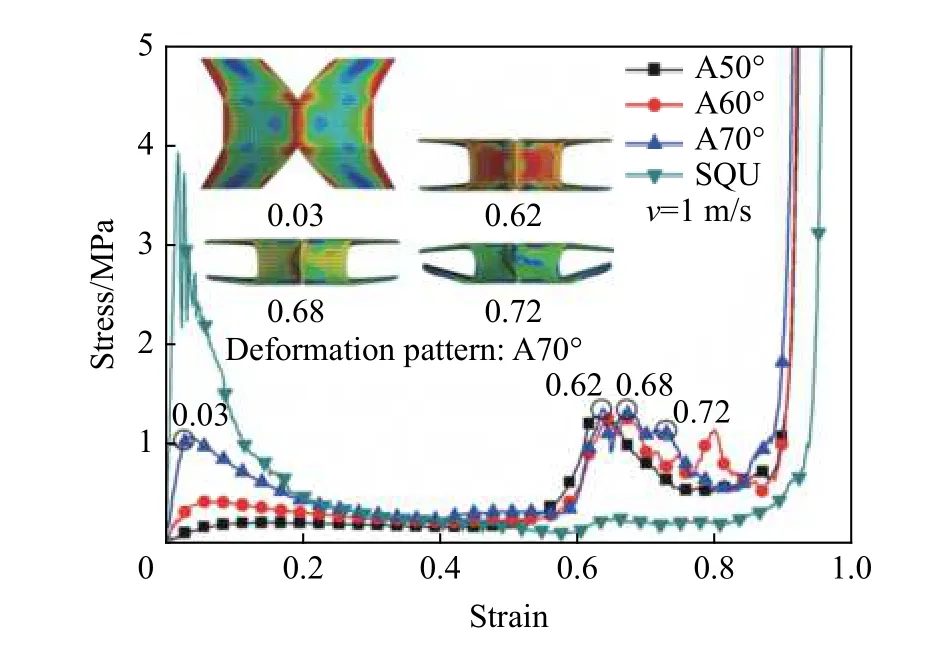
图7 不同单胞模型的应力-应变曲线Fig. 7 Stress-strain curves of different single-cell models

弧形折纸薄壁管和方管面内方向阵列个数n 为2×2 模型的应力-应变曲线如图8 所示（方管阵列采用密排结构，相邻单胞方管间紧密接触，接触位置的壁厚为2 倍的单壁厚（τ），在有限元模型中设置该处壳单元壁厚为2τ），腹板塑性屈曲阶段，A50°、A60°阵列模型在出现第2 个峰值应力之后发生整体坍塌，应力急剧下降，A70°阵列模型竖直管发生整体失稳，第2 平台段应力值变小，由于方管阵列模型中间连接部分腹板壁厚为侧边壁厚的两倍，在压缩过程中，当中间腹板发生整体坍塌时，应力有明显增高，屈曲失稳后失去承载能力，应力迅速下降。所有的弧形折纸薄壁管的第2 平台段应力值均大于方管。图9 为A60°单胞、面内方向阵列个数n 为2×2、4×4 的阵列模型在准静态作用下的应力-应变曲线，由图可知，2×2、4×4 阵列模型的应力应变曲线基本相同，增加面内方向阵列个数对折纸管的应力应变关系没有明显的影响。由于阵列后胞元之间存在一定的横向约束，多胞阵列模型的第一平台段应力明显高于单胞模型，且随着单胞阵列个数的增加，折纸管的第2 平台段应力值明显提高。

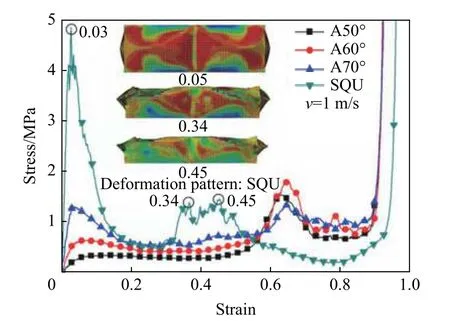
图8 面内方向阵列个数为2×2 的阵列模型的应力-应变曲线Fig. 8 Stress-strain curves corresponding to the models with the number n of in-plane arrays equal to 2×2

图9 面内方向阵列个数不同的A60°模型的应力-应变曲线Fig. 9 Stress-strain curves of different in-plane arrays number of A60° models

3.2.2 冲击速度的影响

图10 为折纸管面内方向阵列个数n=2×2 的阵列模型在冲击速度为10、20 m/s 载荷作用下的应力-应变曲线。从图10 可以看出，折纸管在冲击速度为10 m/s 载荷作用下的初始压溃应力峰值均低于方管的，预折角的变化对折纸管的第1 平台段应力-应变曲线变化趋势及其应力值影响较小。在腹板塑性屈曲阶段，所有折纸管在出现第2 个峰值应力之后发生整体坍塌，应力急剧下降，但第2 平台段应力值均大于方管的。当冲击速度为20 m/s 时，A70°阵列模型在压缩过程中表现出逐层压溃模式，在ε=0.42 时，折纸管上部预折部分首先达到密实化，产生第2 个应力峰值，在ε=0.65 时，折纸管预折部分全部密实化，产生第3 个应力峰值，折纸管的第1、2 平台段应力值均小于方管的。

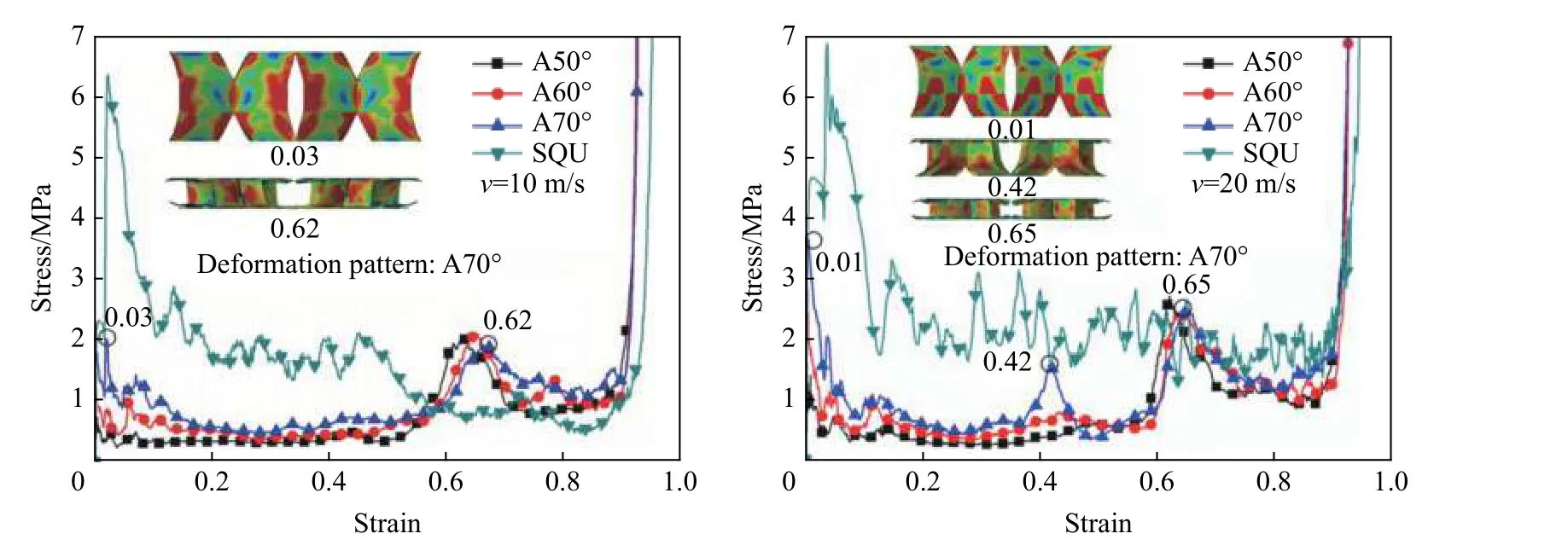
图10 不同冲击速度下，不同阵列模型的应力-应变曲线Fig. 10 Stress-strain curves of different models under different impact velocities

3.2.3 弧形折纸薄壁管和方管的吸能效率

图11～12 为方管和弧形折纸薄壁管的单胞、n=2×2 阵列模型在准静态、冲击速度为10、20 m/s的比吸能对比。从图11～12 可以看出：在准静态压缩作用下，对于单胞模型，A70°在压缩位移约22 mm 之后，比吸能高于方管的，面内方向阵列个数n=2×2 的阵列模型中，方管比吸能优于折纸管；在冲击速度为10、20 m/s 的载荷作用下，n=2×2 的阵列模型中，弧形折纸薄壁管中A70°模型具有较高的比吸能，但方管的比吸能均优于弧形折纸薄壁管。

图11 准静态压缩下不同的单胞薄壁管比吸能随位移的变化Fig. 11 Specific energy absorption varying with displacement for different single-cell thin-walled tubes under quasi-static compression

图12 不同冲击速度下面内方向阵列个数相同的不同薄壁管结构比吸能的对比Fig. 12 Comparison of specific energy absorption for different thin-walled tubes with the same number of in-plane arrays under different impact velocities

对准静态，冲击速度为10、20 m/s 的单胞、面内方向阵列个数n 为2×2 模型的数值模拟采用压缩力效率η 和比总体效率δ 作为薄壁管吸能特性的两种评价指标，压缩效率越大，模型的吸能效果越好。压缩力效率为平均载荷与初始压溃载荷峰值的比值，平均载荷是结构吸收的总能量与最后压缩量之比，比总体效率是单位长度下管的比吸能与初始压溃载荷峰值的比值，所有模型的初始压溃载荷峰值如表2所示。

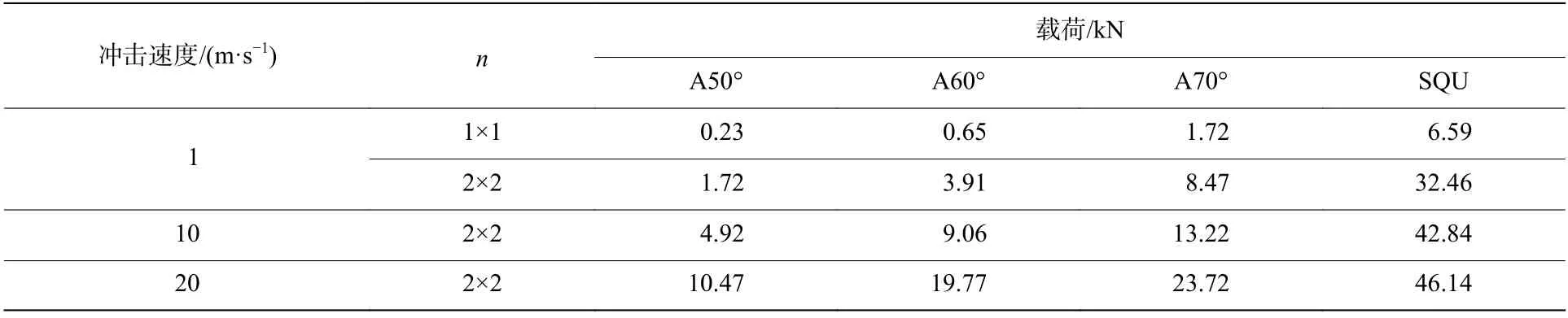
表2 不同模型的初始压溃载荷峰值Table 2 Initial peak crushing loads of different models

图13～14 为弧形折纸薄壁管和方管的压缩力效率-压缩位移曲线，从图中可以看出，在准静态压缩作用下，折纸管单胞及面内方向阵列个数n=2×2 阵列模型的压缩力效率优于方管。在冲击速度为10 m/s 的载荷作用下，A50°阵列模型具有较高的压缩力效率，且所有的弧形折纸薄壁管的压缩力效率均高于方管，如图13 所示。在冲击速度为20 m/s 的载荷作用下，当压缩位移d＜19.73 mm 时，方管阵列模型的压缩力效率高于折纸管，当压缩位移d＞19.73 mm 时，A50°折纸管阵列模型的压缩力效率高于方管，如图14 所示。

图15～16 为弧形折纸薄壁管和方管的比总体效率的比较。从图15 可以看出，在准静态压缩及冲击速度为10 m/s 的载荷作用下，折纸管单胞及面内方向阵列个数n=2×2 阵列模型的比总体效率均优于方管。从图16 可以看出，在冲击速度为20 m/s 的载荷作用下，当压缩位移d＜19.67 mm 时，方管的阵列模型比总体效率高于折纸管，当压缩位移d＞19.67 mm 时，A50°折纸管阵列模型的比总体效率高于方管。

图13 不同薄壁管模型压缩力效率的对比Fig. 13 Comparison of crush force efficiencies for different thin-walled tube models

图14 压缩力效率随压缩位移的变化Fig. 14 Crush force efficiency varying with compressive displacement

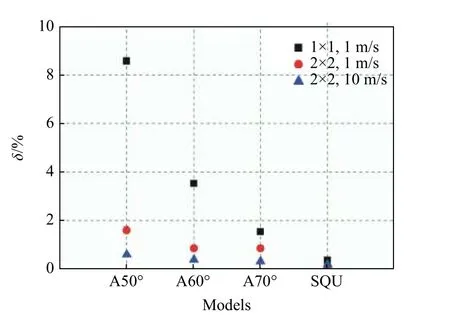
图15 不同薄壁管模型比总体效率的对比Fig. 15 Comparison of specific total efficiencies for different thin-walled tube models

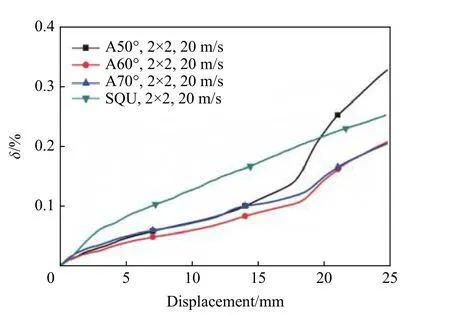
图16 比总体效率随压缩位移的变化Fig. 16 Specific total efficiency varying with compressive displacement

4 结 论

利用3D 打印技术制备了弧形折纸薄壁管件，基于准静态轴向压缩实验，并利用ABAQUS 有限元软件对弧形折纸薄壁管件在准静态，冲击速度10、20 m/s 下的压缩行为进行了数值模拟，探讨了结构的变形模式，分析了不同预折角以及单胞的阵列个数对其变形过程及承载能力的影响，并与高度相等、质量近似相等的方管作对比，得出以下结论。

（1）薄壁管件的变形过程可分为4 个阶段，分别为初始压溃阶段、预折角塑性旋转阶段、腹板塑性屈曲阶段和完全压溃密实化阶段。

（2）设计的弧形折痕能够有效降低初始压溃阶段的载荷峰值，减小压缩载荷-位移曲线在预折角塑性旋转阶段、腹板塑性屈曲阶段的振荡幅值，使结构压缩过程可控、按照预定的弧形折痕发展。

（3）在准静态压缩下：对于单胞模型，A70°模型的比吸能优于方管的；对于多胞管件阵列模型，方管的比吸能均优于折纸管的；折纸管的压缩力效率和比总体效率均优于方管的，且A50°模型的压缩力效率和比总体效率最高。

（4）在本文涉及的动态冲击载荷下，分别通过比吸能、压缩力效率和比总体效率3 个评价指标对比了不同结构的吸能特性：阵列方管的比吸能均优于阵列折纸管的；当冲击速度为10 m/s 时，折纸管的压缩力效率和比总体效率均优于方管的，其中A50°模型的压缩力效率和比总体效率最高；当冲击速度为20 m/s 时，仅有A50°模型的压缩力效率和比总体效率优于方管的。