披上思维的外衣，化“零”为整——整体换元法在高中数学中的应用

徐少珊

(江西省南昌市第二十三中学 江西 南昌 330029)

1.何为整体换元法

顾名思义，整体换元法，是指在具体的数学问题中将有相同规律的某一部分数学表达式当成一个整体，用一个自设的新变量(元)去代替它，放入到原数学关系式中，使原数学问题转化成简单、熟悉的基础数学模型，使问题更加直观化。但是选择换元时的整体要合理且恰当，才能达到简化问题的目的。

2.整体换元法在解题时的应用

整体换元法的应用范围主要是各种复合问题中的求值、求参数范围、解不等式等问题。整体换元法在应用过程中，需要对问题有整体把握和实质了解，才能准确的将问题拆分成多个部分，逐个击破。

例2:已知对任意x，都有sin2x+2kcosx-2k-2<0成立，求k的取值范围。在这道数学题中，出现了多个变量x,sinx,cosx,k为使问题简化，减少变量，可以将其中的sin2x恒等替换成1-cos2x，只要将重复出现的cosx当成整体，令t=cosx(-1≤x≤1)，原不等式简化为1-t2+2kt-2k-2<0，原问题就转化为求t2-2kt+2k+1>0在[-1,1]上恒成立时，求参数k的取值范围，利用一元二次不等式解法，分类讨论就可求参了。在这个整体换元过程中，对二次不等式、同角三角函数之间的关系有一定掌握，才能恰当分解结构，合理进行整体代换。

例3:定义域为R的函数f(x)，对任意实数x都满足：f[f(x)-x2+x]=f(x)-x2+x，并且仅有一个实数x0，使f(x0)=x0成立，求函数f(x)的解析式.

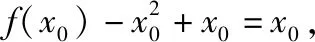
除了以上所举的三个例子，整体换元法在高一学生刚学习二次函数、指数函数、对数函数、三角函数等基本初等函数的图像和性质时，会遇到很多与其相关的复杂函数，求值域、单调区间、参数值等数学问题。在面对这些数学问题时，也都是拆分结构，将某些式子当成整体，采用整体换元的方法来解决。

对式子结构分析，通过运算性质，去掉多余枝节后，将重复出现的结构log2x当成整体，令t=log2x,则原函数转化为“y=t2-2at+a2-1在[a-1,a2-2a+2]上值域为[-1,0]，求实数a的取值范围。”这个二次函数问题，那么只需要知道在对称轴和给定的定义域区间不确定时，值域的最小值和最大值在对称轴和定义域区间的左中右三种位置关系讨论下，分别在区间端点和顶点处取得，检验这三点的值，就可以解决问题了。

3.整体换元法的小结

在整个高中数学学习过程中，还有很多像数列问题：已知数列{an}a1=1,an=2an-1+3n,求通项，圆锥曲线问题等等诸多内容都有整体换元法的应用，整体换元法的应用多而广。掌握好整体换元法最大的好处就是极大限度的降低了解题难度，使复杂数学问题简单化，将原问题划归为更易于求解的一般问题，达到解决问题的目的。

基于整体换元法在数学问题中的重要性，希望教师和同学们在自己的解题实践中有意识归纳和总结，不断完善和更新自己和知识体系，增强化归意识，做到化难为易、化繁为简，使诸多难题迎刃而解。