钢框架连续倒塌分析中全焊接刚性节点的组件模型

谢甫哲，周广杰，顾 斌，雷丽恒

(江苏大学 土木工程与力学学院，江苏 镇江 212013)

当今建筑在服役期内遭受偶然事件(如汽车撞击、炸弹袭击等)的概率不断升高，建筑结构的安全面临着前所未有的挑战.由于偶然事件可能会引起结构发生连续倒塌，造成重大的人员伤亡事件，因此，结构的抗连续倒塌性能越来越受到各国重视.我国GB 50017—2017《钢结构设计标准》和GB 50010—2010《混凝土结构设计规范》都对结构的抗连续倒塌性能提出了要求.自911事件后，国内外学者从结构的破坏机理[1]、设计与评估方法[2]和仿真分析模拟[3]等诸多方面对钢结构的抗连续倒塌性能进行了广泛的研究.大量的研究成果表明节点对钢结构的抗倒塌性能有至关重要的影响[4]，因此，很多学者针对钢框架倒塌过程中节点的受力性能展开研究.陈俊岭等[5]基于理论推导和数值分析，对比了3种节点型式在结构连续倒塌过程中的受力性能，结果表明盖板式节点的抗连续倒塌性能更优越.WANG W.等[6]对采用自锁式单向螺栓连接的H型钢梁与矩形钢管柱节点开展了试验研究，分析了节点在结构倒塌过程中的传力机制、破坏模式和受力性能，结果显示端板连接节点中自锁单向螺栓的性能未能充分发挥.YANG B.等[7]对7种类型的节点开展了试验研究，分析了每种节点在大变形情况下的破坏模式和受力机理，提出了新的拉结承载力表达式.

在对采用刚性连接节点的钢框架结构进行连续倒塌分析时，传统的理想刚性连接节点模型与实际情况不符，因为结构在濒于倒塌时，节点一般处于弹塑性或塑性受力状态[8]，此时节点受力不符合理想刚性连接假定的要求.为考虑节点受力的影响，很多学者基于EN1993-1-8：2005《欧洲规范3：钢结构设计—节点的设计》中的组件法建立节点模型[9-10]，以对钢框架结构抗连续倒塌性能进行更高效、准确地分析.但目前的节点组件模型通常不考虑结构大变形时框架梁内可能产生的轴拉力(即悬链线效应)对节点受力的影响[11]，这不利于对钢结构抗连续倒塌性能进行准确地设计与评估.

在准确模拟全焊接刚性节点试验的基础上，分析梁内轴拉力对节点受力性能的影响；根据全焊接刚性节点在弹塑性阶段的受力机理和变形特点，对传统组件模型进行改进；在此基础上，对节点为理想刚性连接模型、壳单元模型和改进组件模型的钢框架子结构进行静力和动力非线性分析，研究不同节点模型对钢框架结构抗连续倒塌性能的影响，为钢结构抗连续倒塌性研究提供参考.

1 节点试验及分析

1.1 全焊接刚性节点试验

以文献[12]开展的T形梁柱刚性节点试验为基础进行分析研究.试验模型与加载方式如图1[12]所示.试件固定于反力架上，柱两端为铰接连接，梁柱节点为全焊接刚性节点(即文献[12]中的SP4试件).试验中，首先在框架柱顶施加500 kN的压力，再通过往复千斤顶在梁端施加反复荷载.梁和柱的截面尺寸及相关材料特性如表1-2所示，材料的弹性模量均为2.06×105MPa.

图1 试验模型与加载方式示意图(单位：mm)

表1 梁和柱的截面尺寸 mm

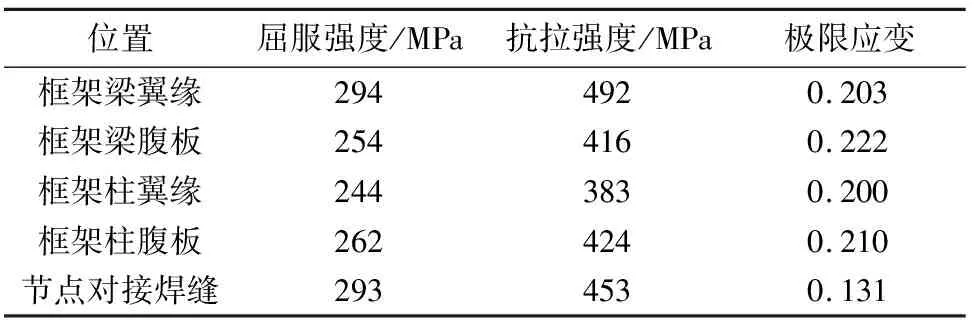
表2 梁、柱及焊缝的材料特性

1.2 壳单元模型及分析

依据试验模型尺寸及边界条件，在Abaqus中建立壳单元模型.图2为壳单元的有限元模型及节点区划分情况.壳单元的类型为S4R和S3，节点区划分的单元尺寸约为25 mm.

图2 壳单元模型及节点区划分情况

图3为壳单元的有限元模型分析结果与试验结果比较.在梁端设置反复位移荷载，对图2中的模型进行静力非线性分析，得到滞回曲线如图3a所示；文献[12]的试验结果如图3b所示.图中Δ为加载点竖向位移，p为梁端反复荷载.

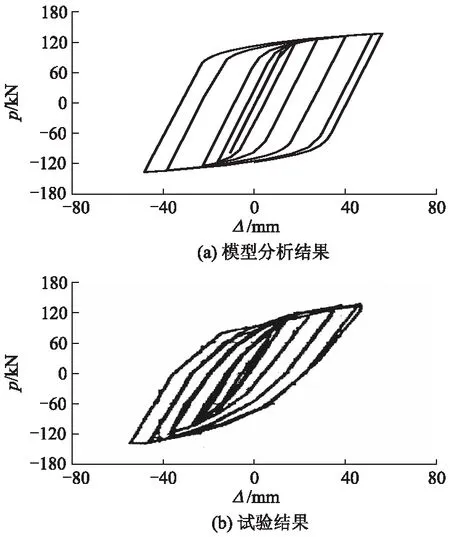
图3 有限元模型分析结果与试验结果比较

由图3可知：由于曲线在弹塑性阶段的倾角比试验结果大，因此有限元模型的刚度略高于试验结果，并且模型滞回曲线比试验滞回曲线更饱满，这主要是由于试件存在初始缺陷(如残余应力)，在实际加载过程中又不可避免地存在偏心等因素造成的.总体上，有限元模型的滞回曲线与试验结果比较吻合，表明壳单元模型可以较真实地反映该节点的受力特性.

1.3 梁内轴拉力对节点受力的影响

为考察结构大变形时框架梁内因悬链线效应产生的轴拉力对节点受力的影响，笔者基于壳单元有限元模型，对节点同时承受不同梁内轴拉力的情况进行分析.图4为考虑框架梁轴拉力影响的节点计算简图，图中Fx为梁端轴向拉力；Fy为梁端竖向荷载.分析结果如图5所示，图5中Fyb为框架梁全截面屈服拉力.

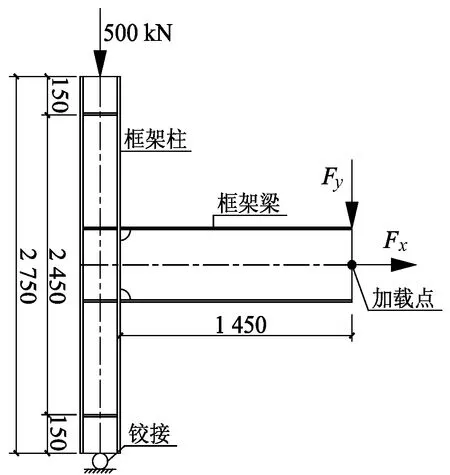
图4 考虑框架梁轴拉力影响的节点计算简图(单位：mm)

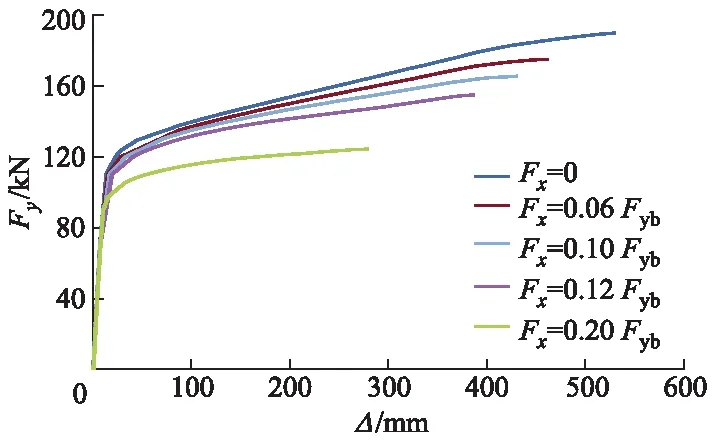
图5 框架梁内不同轴力水平对节点承载力的影响

由图5可知：在弹性阶段，梁内轴拉力对节点受力性能的影响很小；在弹塑性阶段，梁内轴拉力的增大不仅减小了节点的极限承载力，还降低了节点的延性.

2 节点组件模型

节点组件模型是由杆系单元和弹簧单元根据节点的构造和受力组合形成的节点模型,它能够较准确地反映节点受力状态，同时具有较高的计算效率.目前，节点组件模型广泛应用于结构的连续倒塌分析评估.

2.1 全焊接刚性节点组件模型

文献[13]基于H型钢梁柱全焊接刚性连接节点试验，提出了一种简单实用的组件模型.该模型由4根刚性杆和4个转动弹簧组成.图6为全焊接刚性节点组件模型.节点的受力特性主要由4个非线性转动弹簧来模拟.转动弹簧为三折线模型，如图7所示.

图6 全焊接刚性节点组件模型

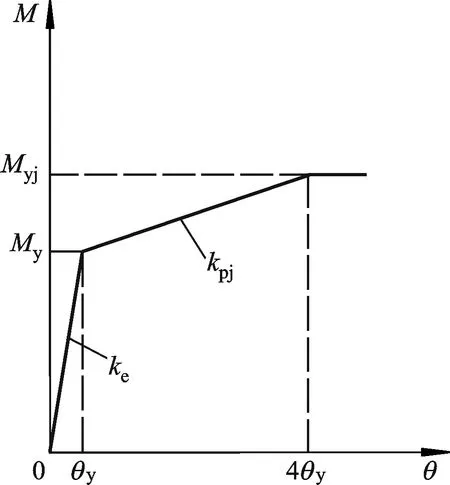
图7 非线性转动弹簧本构模型

图7的节点本构模型中参数的计算公式如下：

(1)

My=0.55dbdctfy，

(2)

(3)

式中：k为转动刚度；My为屈服弯矩；Myj为极限弯矩；dc为框架柱截面高度；db为框架梁截面高度；t为节点域的厚度；tcf为框架柱的翼缘厚度；bc为框架柱的翼缘宽度；θ为弹簧转角，θ=γ，其中γ为节点域的剪切应变；θy为弹簧屈服转角，θy=γy；ke为弹簧单元弹性阶段刚度；kpj为弹簧单元塑性阶段刚度；fy为钢材的抗拉屈服强度；G为钢材的剪切模量；E为钢材的弹性模量.

为检验该节点组件模型分析结果的准确性，笔者基于图1的试验模型，建立节点为组件模型的梁单元模型，如图8所示.根据式(1)-(3)计算得到组件模型的弹簧单元本构参数：ke=18 807 kN·m；kpj=1 243 kN·m；My=32.3 kN·m；Myj=38.8 kN·m；θy=1.71×10-3rad.

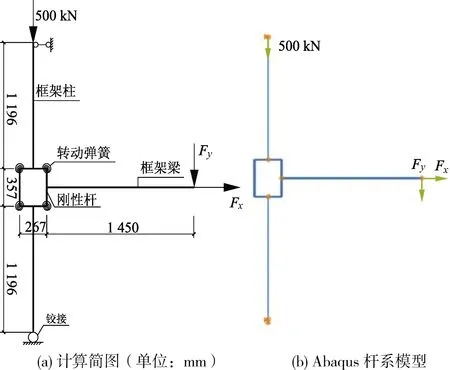
图8 梁单元模型示意图

梁单元和壳单元模型的材料特性参数如下：弹性模量E=206 GPa；屈服强度fy=235 MPa；屈服应变εy=1.14×10-3；极限强度fu=450 MPa；极限应变εu=0.2.

分别对图2壳单元模型和图8b梁单元模型进行静力非线性分析，得到不同轴拉力Fx下的竖向荷载与加载点竖向位移关系曲线，如图9所示.由图9可知：该组件模型(对应图9中的“原节点组件模型”)能够较好地模拟全焊接刚性节点在弹性阶段的受力；在弹塑性阶段，组件模型相对壳单元模型的结果偏高，且节点屈服后变形很小时即达到极限承载力，不能反映结构大变形的情况.

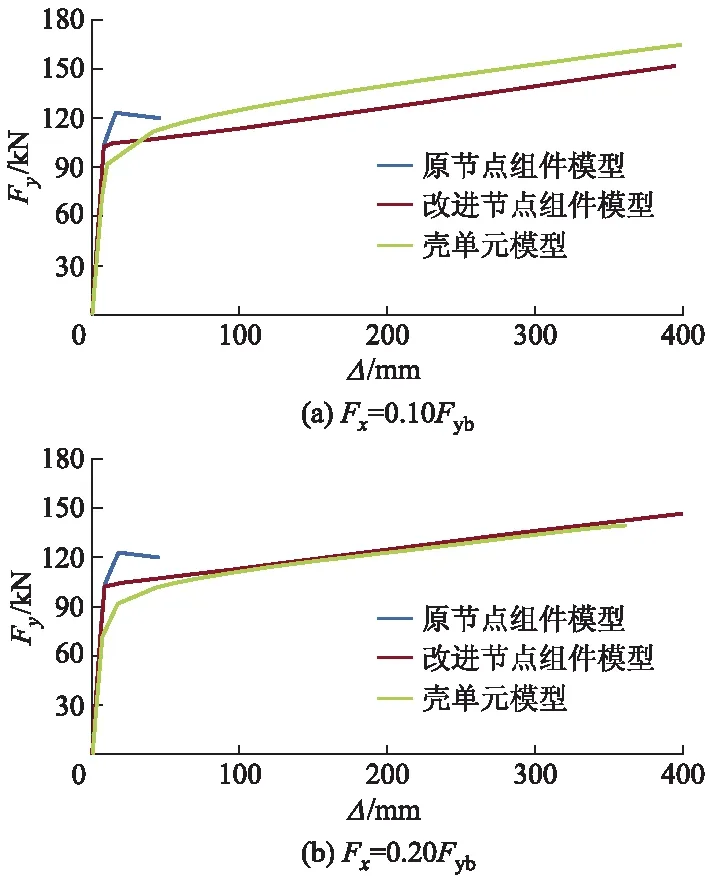
图9 壳单元模型与梁单元模型的荷载-位移曲线

图10为梁柱节点区的变形示意图.原节点组件模型在弹塑性阶段误差大的主要原因如下：① 图7中的弹簧本构模型假定节点在弹塑性阶段的变形和刚度是由4个角点提供(见图10)，而4个角点仅考虑了节点转角达到4γy的情况，这导致节点组件模型在进入弹塑性阶段后仅能反映节点小转角的情况.实际节点的变形除了4个角点的转动外，还有很大一部分是节点域的剪切变形(节点域的剪切角约为角点转角的10倍)；② 实际节点的刚度是考虑节点域的抗剪刚度与角点转动刚度的综合结果，而式(1)在计算刚度kpj时仅基于4个角点的转动刚度，不考虑节点域的剪切刚度，导致节点在弹塑性阶段刚度值偏大.

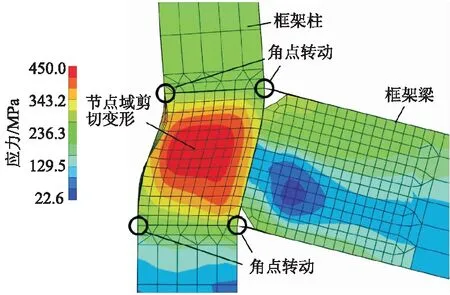
图10 梁柱节点区的变形示意图

2.2 节点组件模型的改进

针对原节点组件模型未能准确反映结构大变形时的受力状态的情况，笔者对图7中的转动弹簧本构模型进行了改进：① 弹性阶段的转动刚度ke及屈服弯矩My与原模型相同；② 弹塑性阶段的刚度kp为角点转动刚度kpj与节点域剪切刚度kpz的并联结果，即

(4)

kpz=0.385(dc-2tcf)tEt，

(5)

式中：Et为切线模量.

根据式(4)和(5)计算得到改进节点组件模型的弹簧参数如下：ke=18 807 kN·m；kp=84 kN·m；My=32.3 kN·m；θy=1.71×10-3rad.基于改进节点组件模型的弹簧参数，对图8模型进行分析，得到结构的荷载-位移曲线(见图9).由图9可知，改进节点组件模型的分析结果与壳单元模型的结果接近，表明节点组件模型能较好地模拟全焊接刚性节点的弹塑性受力状态.

3 梁柱子结构静力与动力非线性分析

3.1 静力非线性分析

基于图1的计算模型，建立钢框架子结构模型，如图11所示.边柱上下两端铰接，柱顶作用压力为500 kN.分别对壳单元模型和梁单元模型进行静力非线性分析(包括理想刚性连接节点模型和改进节点组件模型两种)，考虑中间框架柱失效，在其顶部施加逐渐增大的竖向荷载Fy.子结构模型中构件的材料特性与图8模型中构件的材料特性相同；改进节点组件模型的弹簧参数取值与前文2.2节中弹簧参数值相同.

图11 静力分析的子结构模型(单位：mm)

静力非线性分析结果表明子结构的变形主要有两个阶段：① 开始时主要为节点区域的剪切变形；② 在失效柱竖向位移达到约0.6 m后，结构的变形主要为框架柱的弯曲变形.图12为3种模型在最大竖向位移相近时的弹塑性阶段变形情况.由图可见，节点组件模型可以较好地反映节点区的剪切变形，而节点为理想刚性连接的子结构模型则仅为梁、柱构件自身的变形.

图12 子结构模型静力分析的变形情况

壳单元和梁单元子结构模型的静力分析竖向荷载与失效柱竖向位移关系曲线如图13所示，图中Fx为失效柱竖向位移Δs对应的梁内轴拉力.由图13可知，3种模型在弹性阶段的受力基本相同，因此，理想刚性连接节点可用于对钢框架抗倒塌性能的弹性分析评估；在弹塑性阶段，理想刚性连接节点由于未能反映节点的弹塑性受力，使得结构的承载力偏高(使失效柱产生相同竖向位移，理想刚性连接模型比壳单元模型的竖向荷载大15%～25%)，分析结果偏不安全.由图13还可知，即使梁内因悬链线效应而产生轴拉力，改进节点组件模型仍能够较准确地反映钢框架子结构在静力荷载作用下的受力状态.相对于壳单元模型，采用改进节点组件模型的梁单元模型的刚度稍微偏大：竖向荷载相同，改进节点组件模型的竖向位移偏小，减小约8%；竖向位移相同，改进节点组件模型的竖向荷载偏大，增大约5%.这主要是由于节点组件模型的四周均为刚性杆，忽略了节点周边板件(如加劲肋、柱翼缘等)变形的影响.

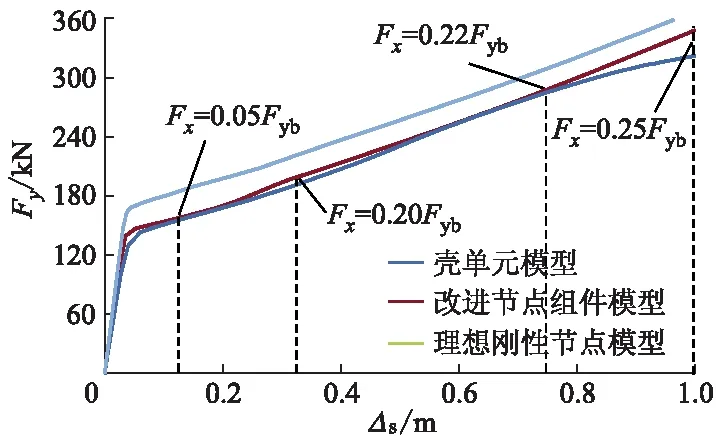
图13 子结构模型的静力荷载-位移曲线

3.2 动力非线性分析

图14为动力非线性分析的子结构模型及失效时间.进一步对子结构进行动力非线性分析，计算模型如图14a所示.计算过程分两个分析步：① 结构初始受力状态分析.在中间失效框架柱顶施加竖向压力160 kN，同时在中间框架柱底施加反作用力F0(由静力分析得到)，钢材特性及边界条件等均与图11的模型相同.采用准静态分析法分别对壳单元模型和梁单元模型进行非线性分析，得到结构在中间框架柱失效前的初始受力状态.② 中间框架柱突然失效后剩余结构受力状态分析.为得到结构的最大动力效应，将中间框架柱的柱底反作用力在0.001 s内减小至0，如图14b所示，Δt=0.001 s，通过显式动力法对结构进行计算分析，得到失效柱竖向位移的时程曲线，如图15所示.

图14 动力非线性分析的子结构模型及失效时间

图15 失效框架柱竖向位移时程曲线

由图15可知：节点为理想刚性连接的梁单元模型最大竖向位移为170 mm，明显小于壳单元模型，误差约为53%；节点为改进组件模型的梁单元模型最大竖向位移为334 mm，与壳单元模型的结果(360 mm)接近，误差约为7.2%，表明改进节点组件模型适用于模拟节点在结构受瞬时动力作用下的弹塑性受力状态.

4 结 论

1)框架梁内的轴拉力不仅削弱节点的承载力，还会降低节点的延性，在对结构进行连续倒塌分析时，应考虑梁内轴拉力的影响.

2)全焊接刚性节点在弹塑性阶段的变形主要有4个角点的转动变形和节点域的剪切变形，并且以剪切变形为主.

3)传统全焊接刚性节点的组件模型可以较好地模拟节点弹性阶段的受力，但不能准确反映结构大变形时节点的弹塑性受力状态；理想刚性连接节点可用于对钢框架抗倒塌性能的弹性分析评估，但用于结构的弹塑性分析时，其结果误差较大，且偏不安全.

4)采用全焊接刚性节点的钢框架结构在倒塌过程中的变形主要有两个阶段：第1阶段以节点区的变形为主；第2阶段以梁、柱构件自身的拉伸与弯曲变形为主.

5)改进节点组件模型，能够较准确地反映全焊接刚性节点在结构连续倒塌分析时的受力状态.