基于实测数据的混凝土曲线梁桥温差代表值研究

孙增寿，夏云飞，韩培琰

基于实测数据的混凝土曲线梁桥温差代表值研究

孙增寿1，夏云飞1，韩培琰2

(1. 郑州大学 土木工程学院，河南 郑州 450001；2. 中铁四局集团 第一工程有限公司，安徽 合肥 230000)

针对曲线梁桥在温度荷载作用下产生竖向变形、切向位移和横向位移，且横向位移严重影响曲线梁桥安全性与耐久性的问题，为确定曲线梁桥日温差的分布规律，用光纤传感器对一座沥青铺装的预应力混凝土在役曲线梁桥进行1 a的温度数据实时监测, 并采用聚类分析、参数估计和假设检验等方法对曲线梁桥温差代表值进行分析计算。研究结果表明：沥青铺装预应力混凝土在役曲线梁桥竖向和横向日最大正温差服从两参数的Weibull分布，竖向日最大正温差标准值为21.7 ℃，频遇值为21.4 ℃，准永久值为20.3 ℃。横向日最大温差标准值为14.1 ℃，频遇值为13.7 ℃，准永久值为12.6 ℃，横向温差标准值占竖向的64.9%，对中原区域曲线梁桥设计计算中温度的取值提供了依据。

曲线梁桥；实测数据；温差；聚类分析；Weibull分布

曲线梁桥造型优美，经济实用，在建造城市立交和高架匝道桥时备受青睐，但随着时间的推移，曲线梁桥经常会发生爬移，严重影响了曲线梁桥及下部桥墩的受力和安全性能，给桥梁结构及行车带来了安全隐患[1]。曲线梁桥在使用中，不仅会产生竖向变形，还会发生桥梁纵向的切向位移和曲率半径方向的横向爬移，其中横向爬移是曲线梁桥最应该关注的，横向爬移的累积和加剧将导致曲线梁桥的破坏。导致爬移的原因很多，其中温差效应是曲线梁桥发生爬移的主要原因之一[2−3]，也是设计计算中必须考虑的因素。国内外很多学者发现，《公路桥涵设计通用规范》中规定的温差取值与当地环境区别很大，因此有必要确定该地区曲线梁桥温差代表值，以便对曲线梁桥可能的爬移进行分析计算和预警。《公路桥涵设计通用规范》对温度的作用形式规定如下：计算桥梁结构竖向温度效应时，采用如图1(a)所示的温度梯度曲线，当梁高＜400 mm，=−100，当梁高≥400 mm，=300 mm。计算桥梁结构横向温度效应时，采用如图1(b)所示的温度梯度曲线，1和2取值见表1[4]。90 mm厚沥青铺装层的混凝土箱梁，其竖向最大温差标准值为15.2 ℃，横向温差标准值为6.75 ℃。但以往研究[5−8]温度作用时通常只考虑竖向温差，忽略横向温差，并且多是根据数天的数据为研究对象，采用曲线拟合的方法来得到温度梯度分布，对于在役曲线梁桥温度梯度的实际分布采用统计学方法来计算温差代表值的研究较少[9−12]。为了确定在役曲线梁桥温差的分布规律，本文对一座90 mm沥青铺装的预应力混凝土在役曲线梁桥光纤光栅传感器1 a的实测温度数据进行分析研究。

图1 箱梁温度梯度

表1　温度梯度基数

1 工程概况及传感器布设

1.1 工程概况

郑州市某匝道曲线梁桥于2004年10月竣工通车，桥梁全长1 202.7 m，共有12联43跨，桥宽为9.5 m。该曲线梁桥上部结构为预应力混凝土斜腹板连续箱梁，断面布置为单箱单室，每联之间采用牛腿搭接，并且在牛腿处设置了伸缩缝。下部结构为花瓶型独柱墩。桥梁在服役过程中，发生了较大的横向爬移，导致支座破坏、伸缩缝错位以及桥墩底部开裂，其中35号墩横向爬移220 mm。在2015年，采用顶推法部分复位和加大墩截面对病害进行了处理，并且为了监测处理后桥梁的爬移情况和健康状况，安装了光纤光栅传感器和健康监测系统，对爬移、纵向位移、加速度、温度等数据进行观测。该匝道平曲线半径=300 m，桥跨布置为37.5 m+45.7 m+45.7 m+37.5 m，支座采用盆式橡胶支座，支座布置形式见表2。其中DX为单向支座，SX为双向支座，GD为固定支座，支座横向间距为2.0 m。

表2　支座布置形式

1.2 传感器布置

该匝道曲线梁桥属于超静定结构，在太阳暴晒下，顶底板内外侧会受热不均，存在温度场，温度场对横向位移和应力应变的影响较大。所以在34号墩与35号墩之间箱梁的跨中截面设置温度传感器，安装位置如图2所示，S1位于箱梁内侧上翼缘板板顶处，S2位于上翼缘板与腹板交界处腹板表面，S3和S4位于箱梁底板内外侧表面，S5悬空置于内部中间，测箱室内温度。

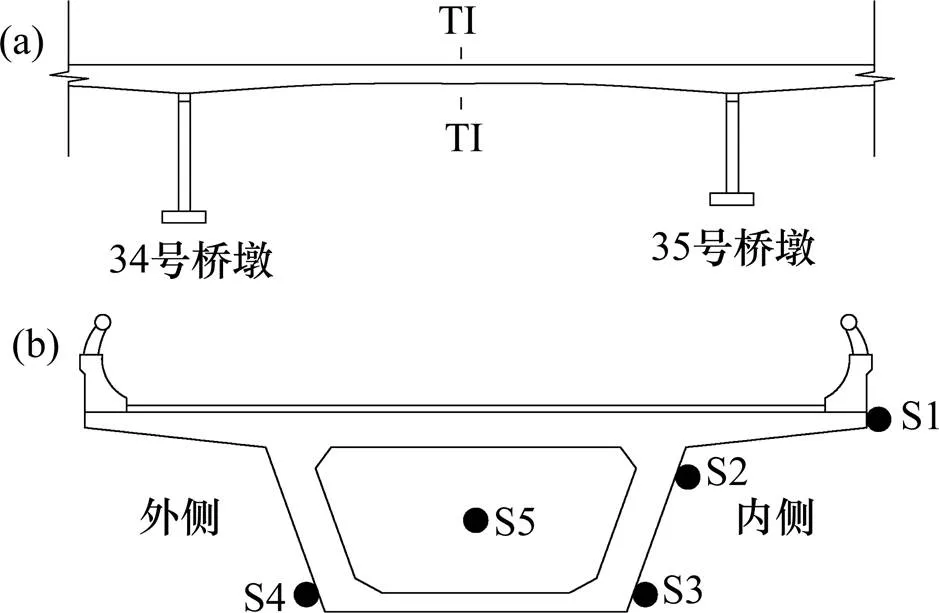
(a) 纵断面；(b) 横断面

郑州属暖温带大陆性气候，光照充足，四季分明，冬季寒冷而干燥，夏季炎热多雨。年平均气温为14.3 ℃，7月份最热，月平均气温27.3 ℃，1月份最冷，月平均气温为−0.2 ℃。

2015年9月传感器布设完成，用现场配备的数据解调仪进行光纤信号解析和测量。采样频率为6次/min，本文数据是2015年10月15日至2016年9月17日将近1a的实测数据。

2 曲线梁桥日最大正温差分析

2.1 日最大正温差数据分析

对采集的每一天数据进行处理，得到每天的日最大温差[13]。日最大温差包括竖向日最大正温差和横向日最大正温差，竖向日最大正温差为34号墩~35号墩跨中截面顶底板的最大差值，即S1，S2和S3最大差值，横向日最大正温差为34号墩~35号墩跨中截面内外侧底板最大差值，即S3和S4最大差值。由于日照作用，温差的变化较大，故在选择样本时，尽量选择晴天的数据。混凝土箱梁竖向日最大温差随时间的变化如图3(a)所示，横向日最大正温差如图3(b)所示。从图3可知，随时间变化，曲线梁桥箱梁的竖向日最大温差接近一条正弦曲线，冬季日最大正温差高于夏季。曲线梁桥箱梁的横向冬季日最大温差也大于夏季。

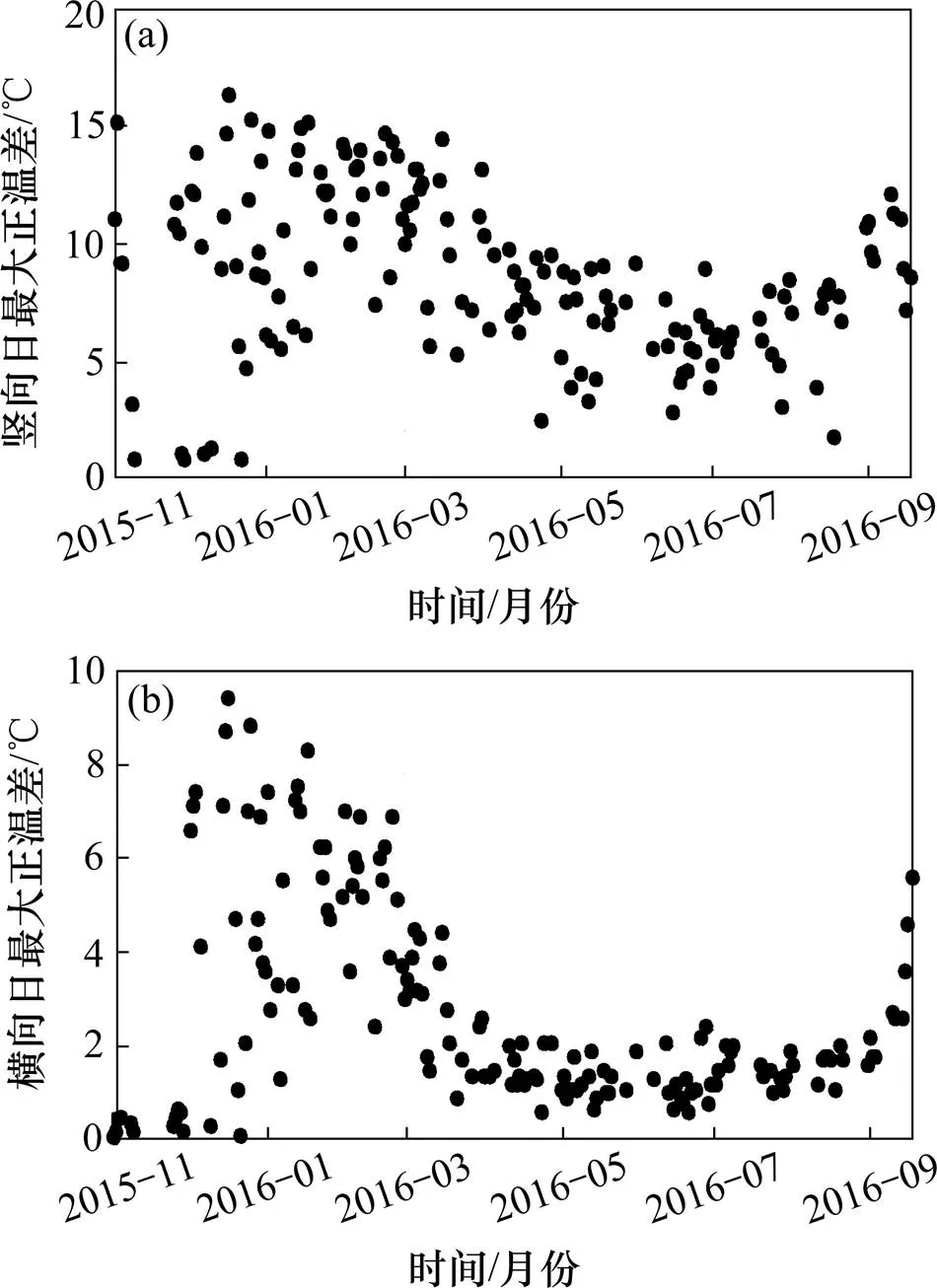
(a) 竖向；(b) 横向

2.2 聚类分析分组

以往研究[14]实测数据的分布规律，常常需要对数据进行分类。聚类分析是将物理量分为类似组的分析过程，不需要事先给出分类标准，它以数据样本出发，自动进行快速分类，对该实测数据适用。实测数据每一个月气温变化不大，为了便于处理，把每一个月作为1组进行分析，预分组见表3，共10组数据。

对预分组的数据进行聚类分析，分别得到各月的竖向和横向日最大正温差相似树图，竖向相似树图如图4(a)所示，横向相似树图如图4(b)所示。由图4可知，竖向温差数据可以分为2类，第1类为1，2，3，4和5组，即2015年11月~2016年3月，称之为冬季数据；第2类为6，7，8，9和10组，即2016年4月~9月，称之为夏季数据。横向温差分布规律与竖向略有不同，2，3和4组数据较为接近，分为第1类，即2015年12月~2016年2月。而1和5组的横向温差分布与6，7，8，9和10组接近，故分为第2类，即2015年11月，2016年3月~9月。冬季数据均比夏季数据离散性大，和图3显示的规律相同，并依据非参数秩和检验来验证冬、夏季数据分布函数的差异。结果表明冬季数据和夏季数据具有不同的分布函数，应当分别考虑。

表3　日最大温差的预分组

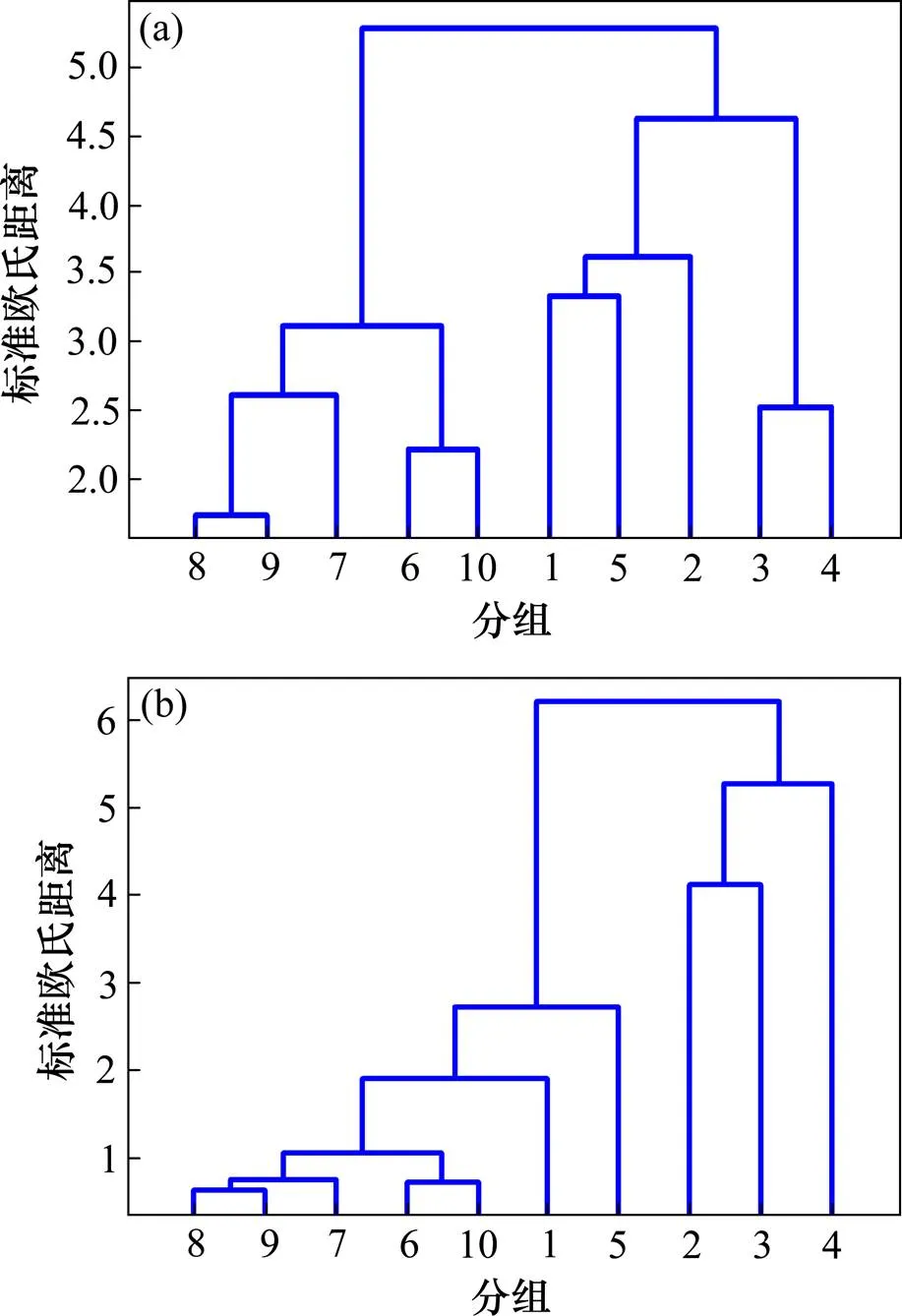
(a) 竖向温差；(b) 横向温差

2.3 分布函数的拟合

以往研究温差数据符合Weibull分布[15]，假定该曲线箱梁桥温差数据服从Weibull分布。Weibull分布有1参数Weibull，2参数Weibull，3参数Weibull和混合Weibull多种形式，3参数的Weibull分布包括形状参数，尺度参数和位置参数；2参数的Weibull分布包括形状参数，尺度参数，通常用(,)表示。形状参数确定了分布的形状(＞0)，尺度参数确定曲线的大小(＞0)。2参数的Weibull分布既能保证数据的完整性，又能简便快速地拟合出结果，故该实测数据采用2参数的Weibull分布。

(,)分布函数为：

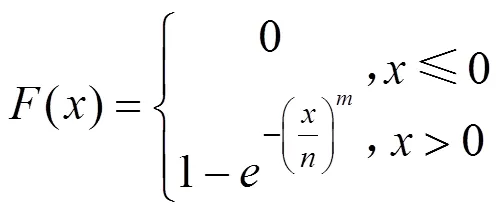
(,)概率函数为：

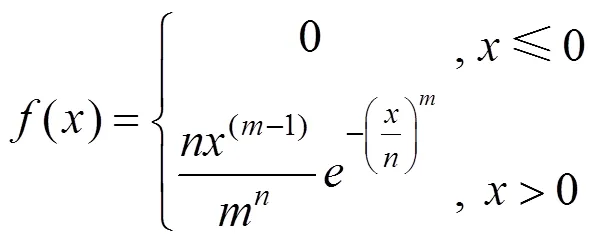
把前面得到的竖向温差样本数据和横向温差样本数据分别绘制在Weibull概率密度纸上，竖向样本数据如图5所示，横向样本数据如图6所示。由图5~6可知，竖向和横向温差数据分布均接近一条直线，则有理由假设样本数据服从Weibull分布。

根据样本数据进行拟合分析，得到曲线梁桥竖向冬季日最大正温差服从参数为(12.117 3,4.491 1)的Weibull分布，夏季日最大正温差服从参数为(7.781 4,3.685 8)的Weibull分布。横向冬季日最大正温差服从参数为(5.783 1,2.871 8)的Weibull分布，夏季日最大正温差服从参数为(1.772 2,2.566 9)的Weibull分布。概率密度函数参数见表4。

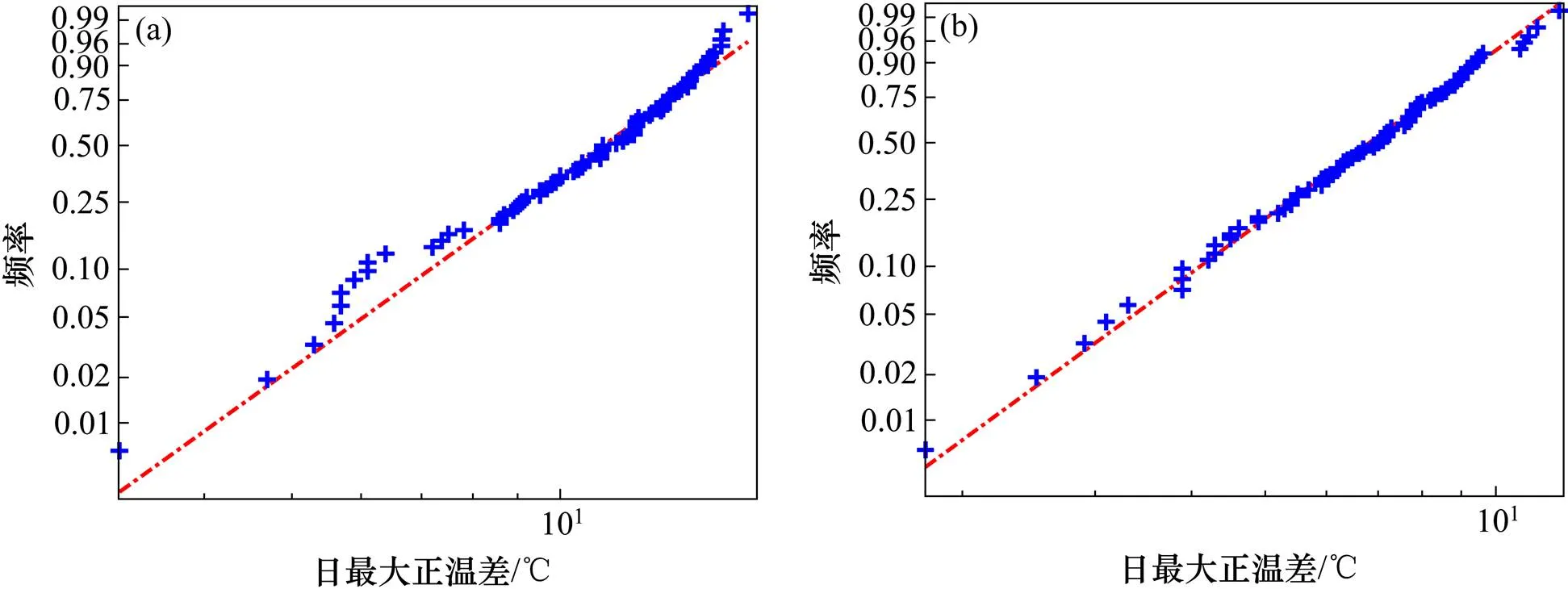
(a) 竖向冬季；(b) 竖向夏季

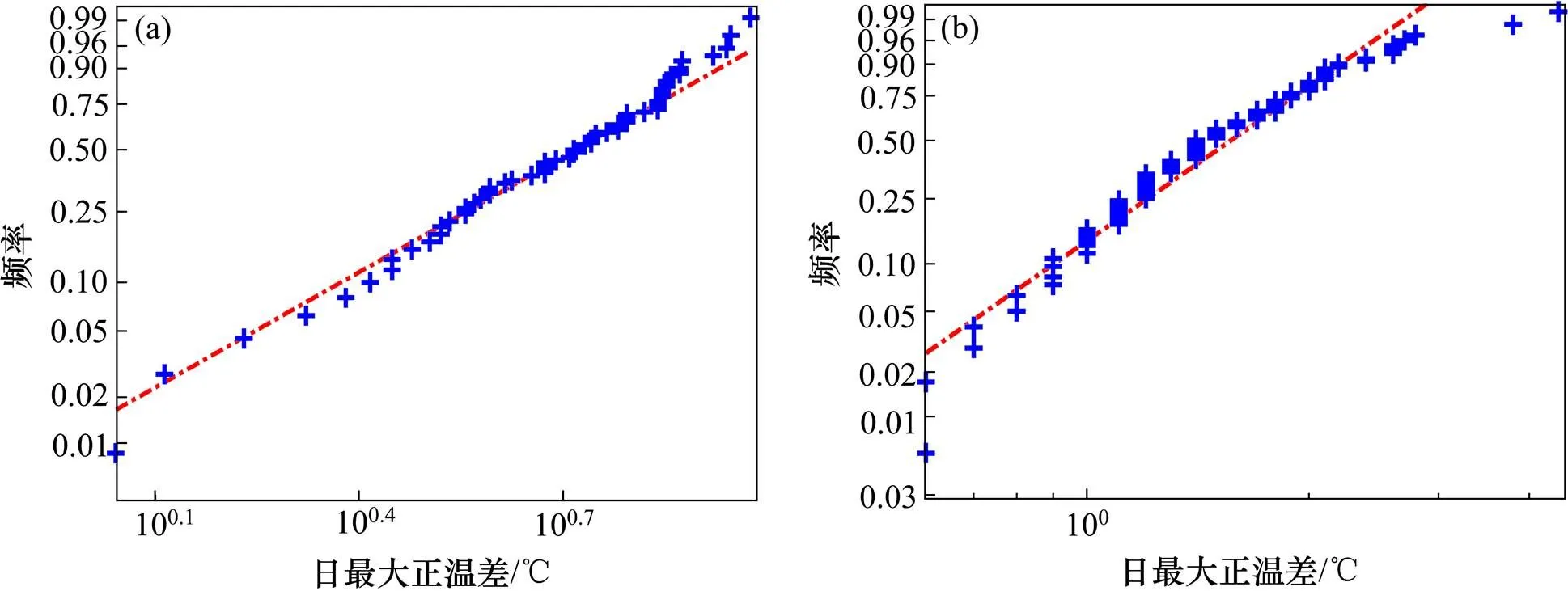
(a) 横向冬季；(b) 横向夏季

表4 各分组参数

竖向冬季日最大正温差概率密度函数如图7所示。竖向夏季日最大正温差概率密度函数如图8所示。

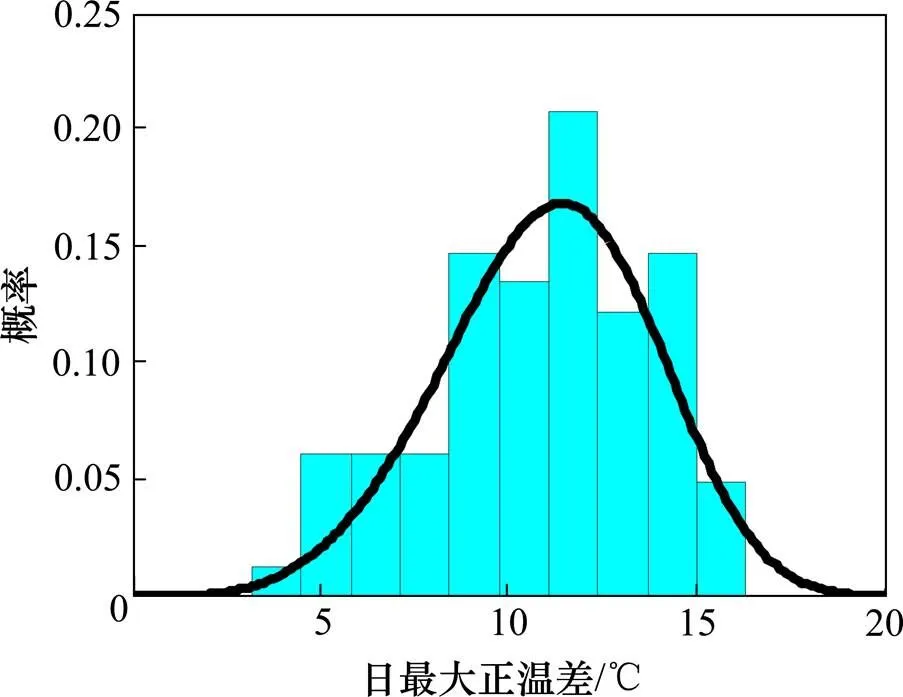
图7 冬季日最大正温差概率密度函数

图8 夏季日最大正温差概率密度函数

横向冬季日最大正温差概率密度函数如图9所示。横向夏季日最大正温差概率密度函数如图10所示。

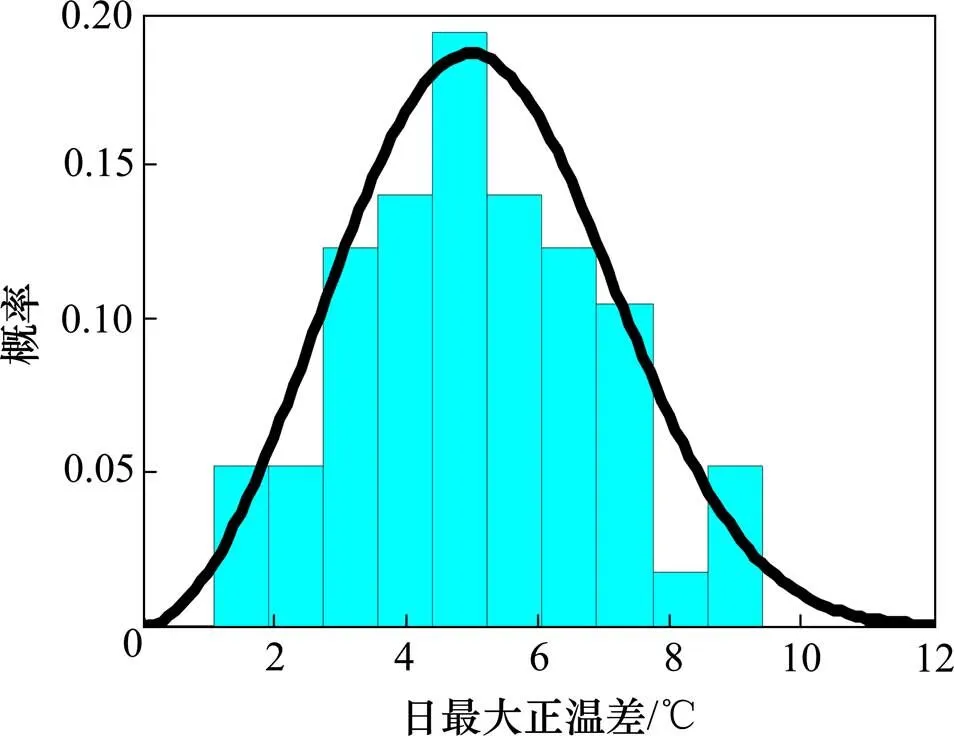
图9 冬季日最大正温差概率密度函数

2.4 曲线梁桥温差代表值的计算

该地区曲线梁桥最大温差值通过超越概率方法来确定。具体计算步骤为：设随机变量X为第天的日最大正温差，每一天的分布函数为()，即上述竖向冬季、竖向夏季、横向冬季和横向夏季温差的分布函数。若桥梁设计基准期按100 a来计算，在设计基准期内任意一天作为一个样本值，则样本值组成的一个样本组为(1,2,3,…,36 500)，设计基准期内最大温差值可表示为=MAX(1,2,3,…,365 00)，的分布函数为：

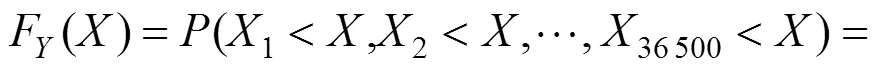
(3)

对于该曲线箱梁桥的竖向温差，假设设计基准期内冬季样本和夏季样本数据量相同，s表示夏季样本，W表示冬季样本。则上式可以写为：

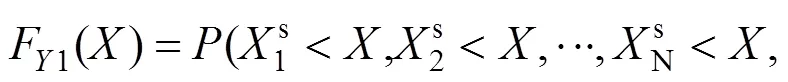
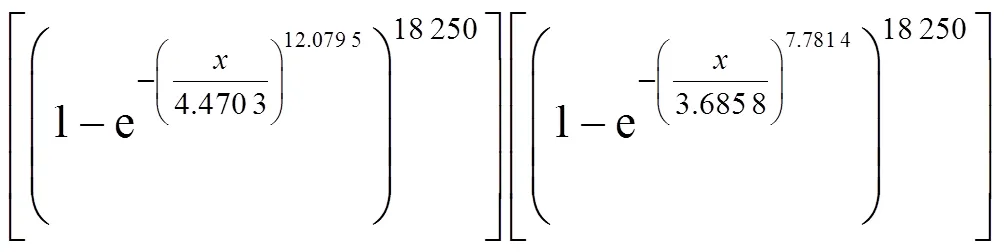
对于该曲线箱梁桥的横向温差，假设设计基准期内冬季样本是夏季样本数据量的1/4，则上式可以写为：

令MAX大于给定温差的概率为，即为超越概率。给定温差的确定方法，用下式确定：

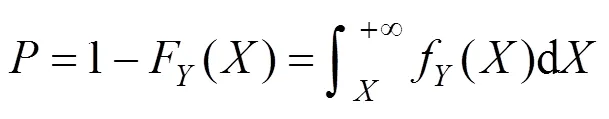
对于竖向温差

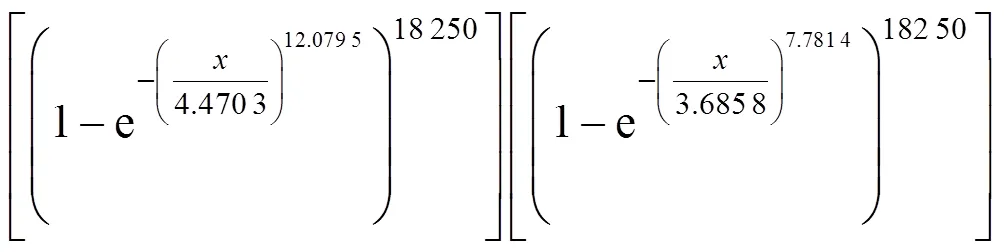
对于横向温差

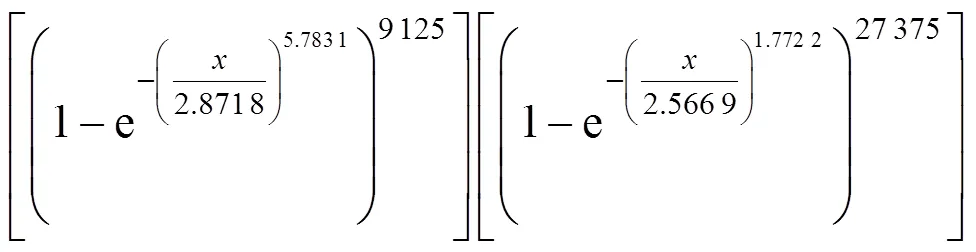
混凝土曲线梁桥在设计基准期竖向最大正温差MAX的概率分布如图11(a)所示，横向如图11(b)所示。

(a) 竖向；(b) 横向

图11 最大正温差概率

Fig. 11 Maximum positive temperature difference probability map

温差标准值最早由欧洲规范提出并计算，而欧洲规范所采用的设计基准期为50 a，不同于该曲线箱梁桥设计基准期为100 a，按欧洲规范超越了2次，也就是说，超越概率1=2%。温差准永久值根据在设计基准期内达到或超过设计基准期的50%，也就是说，超越概率2=50%。温差频遇值根据在设计基准期内达到或超过设计基准期的5%，也就是说，超越概率3=5%。根据式(6)分别求得竖向各代表值，竖向温差标准值为21.7 ℃，温差频遇值为21.4 ℃，温差准永久值为20.3 ℃。则该区域曲线梁桥混凝土箱梁日最大温差值见表5，并与规范值进行了比较。

表5　各温差代表值

同样运用上述方法和式(7)分别计算得到横向温差标准值为14.1 ℃，温差频遇值为13.7 ℃，温差准永久值为12.6 ℃，横向温差代表值比竖向温差代表值约少1/3。

从表5及计算结果可知，本文所研究曲线梁桥的最高温差大于《公路桥涵设计通用规范》关于温差值的规定。根据跨中截面实测应力数据分析显示，竖向、横向温度应力水平较规范温差值对应应力水平分别大31.6%和39.2%，说明按规范计算偏于不安全，分析计算结果对中原区域以及地域、气候相似地区曲线梁桥的设计具有一定参考价值。

3 结论

1) 根据光纤传感器长期监测数据，可采用聚类分析、参数估计和假设检验等统计学方法计算曲线梁桥竖向、横向温差代表值。

2) 曲线梁桥竖向冬季、竖向夏季、横向冬季和横向夏季温差分布规律有所不同。混凝土箱梁竖向冬季日最大温差服从参数为(12.117 3,4.491 1)的Weibull分布，竖向夏季日最大温差服从参数为(7.686 6,3.606 7)的Weibull分布。横向冬季日最大正温差服从参数为(5.783 1,2.871 8)的Weibull分布，夏季日最大正温差服从参数为(1.772 2,2.566 9)的Weibull分布。

3) 90 mm厚沥青混凝土铺装层箱梁的竖向最大温差标准值为21.7 ℃，频遇值为21.4 ℃，准永久值为20.3 ℃。横向最大温差标准值为14.1 ℃，频遇值为13.7 ℃，准永久值为12.6 ℃。

4) 计算所得温差代表值适用于中原区域曲线梁桥，对地域、气候相似地区曲线梁桥的设计具有一定参考价值。

[1] 焦驰宇, 刘陆宇, 龙佩恒, 等.城市曲线梁桥爬移现象及解决措施研究[J]. 工程力学, 2015, 32(增1): 177− 183. JIAO Chiyu, LIU Luyu, LONG Peiheng, et al. Study on the phenomenon of urban curve beam bridge creep and its solution[J]. Engineering Mechanics, 2015, 32(Suppl 1): 177−183.

[2] 刘奎. 小半径曲线梁桥力学性能及局部分析研究[D].南京: 东南大学, 2018. LIU Kui. Mechanical properties and local analysis of small radius curved beam bridges[D]. Nanjing: Southeast University, 2018.

[3] 庞振宇, 徐秀丽, 邢世玲, 等. 城市混凝土曲线梁桥温度场及温度效应分析[J]. 中外公路, 2016, 36(1): 124− 130. PANG Zhenyu, XU Xiuli, XING Shiling, et al. Analysis of temperature field and temperature effect of urban concrete curved beam bridge[J]. China Foreign Highway, 2016, 36(1): 124−130.

[4] JTGD60—2015, 公路桥涵设计通用规范[S].JTGD60—2015, General specification for design of highway bridges and culverts[S].

[5] 肖新辉, 刘扬, 郭鑫, 等. 组合高墩大跨连续刚构桥箱梁日照温度场观测与效应分析[J]. 铁道科学与工程学报, 2014, 11(1): 10−16. XIAO Xinhui, LIU Yang, GUO Xin, et al. Analysis and effect analysis of sunshine temperature field of box girder with high pier and long span continuous rigid frame bridge[J]. Journal of Railway Science and Engineering, 2014, 11(1): 10−16.

[6] 周广东, 李爱群, 丁幼亮, 等. 基于实测数据的润扬大桥悬索桥全寿命评估随机温度场模拟[J]. 东南大学学报(自然科学版), 2013, 43(5): 912−916. ZHOU Guangdong, LI Aiqun, DING Youliang, et al. Simulation of stochastic temperature field for life assessment of suspension bridge of Runyang Bridge based on measured data[J]. Journal of Southeast University (Natural Science Edition), 2013(5): 912−916.

[7] 丁幼亮, 王高新, 周广东. 基于长期监测数据的润扬大桥扁平钢箱梁温度分布特性[J]. 中国公路学报, 2013, 26(2): 94−101. DING Youliang, WANG Gaoxin, ZHOU Guangdong. Temperature distribution characteristics of flat steel Box girder of Runyang Bridge based on long-term monitoring data[J]. China Journal of Highway and Transport, 2013, 26(2): 94−101.

[8] Abid S, Taysi N, Ozakca M. Experimental analysis of temperature gradients in concrete box-girders[J]. Construction & Building Materials, 2016, 106(C): 523− 532.

[9] 顾颖, 李亚东, 姚昌荣. 太阳辐射下混凝土箱梁温度场研究[J]. 公路交通科技, 2016, 33(2): 46−53. GU Ying, LI Yadong, YAO Changrong. Research on temperature field of concrete box girder under solar radiation[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 46−53.

[10] 刘森林. 基于监测数据的长大跨桥梁温度应力分析与安全评价[D]. 南京: 东南大学, 2017. LIU Senlin. Temperature stress analysis and safety evaluation of long and long bridges based on monitoring data[D]. Nanjing: Southeast University, 2017.

[11] 董旭, 邓振全, 李树忱. 大跨波形钢腹板箱梁桥日照温度场及温差效应研究[J]. 工程力学, 2017, 34(9): 239− 247. DONG Xu, DENG Zhenquan, LI Shucheng. Study on sunshine temperature field and temperature difference effect of long span corrugated steel web box girder bridge[J]. Engineering Mechanics, 2017, 34(9): 239−247.

[12] 刘扬, 张海萍, 邓扬, 等. 基于实测数据的悬索桥钢箱梁温度场特性研究[J]. 中国公路学报, 2017, 30(3): 56− 64. LIU Yang, ZHANG Haiping, DENG Yang, et al. Study on temperature field characteristics of steel box girder of suspension bridge based on measured data[J]. Journal of Chinese Highway Society, 2017, 30(3): 56−64.

[13] 雷笑, 叶见曙, 王毅. 日照作用下混凝土箱梁的温差代表值[J]. 东南大学学报(自然科学版)2008, 38(6): 1105−1109. LEI Xiao, YE Jianshu, WANG Yi. The representative value of temperature difference of concrete box girder under the action of sunshine[J]. Journal of Southeast University (Natural Science Edition), 2008, 38(6): 1105− 1109.

[14] 叶见曙, 雷笑, 王毅. 基于统计分析的混凝土箱梁温差标准值研究[J]. 公路交通科技, 2009, 26(11): 50−54. YE Jianshu, LEI Xiao, WANG Yi. Study on the standard value of temperature difference of concrete box girder based on statistical analysis[J]. Journal of Highway and Transportation, 2009, 26(11): 50−54.

[15] 周广东, 丁幼亮, 李爱群. 基于长期实测数据的大跨悬索桥扁平钢箱梁温差特性研究[J]. 土木工程学报, 2012, 45(5): 114−125. ZHOU Guangdong, DING Youliang, LI Aiqun. Research on temperature difference characteristics of flat steel box girder of long-span suspension bridge based on long-term measured data[J]. China Civil Engineering Journal, 2012, 45 (5): 114−125.

Research on representative value of temperature difference of concrete curved beam bridge based on measured data

SUN Zengshou1, XIA Yunfei1, HAN Peiyan2

(1. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China;2. China Railway Fourth Bureau Group First Engineering Co. Ltd, Hefei 230000, China)

For the curved beam bridge under the action of temperature load, vertical deformation, tangential displacement and lateral displacement will occur, and the lateral displacement will seriously affect the safety and durability of the curved beam bridge. In this paper, a fiber-optic sensor was used to monitor the prestressed concrete in-service curve beam bridge of an asphalt pavement in real time. And a year temperature data was recorded. The representative values of the temperature difference of the curved beam bridge were analyzed and calculated by cluster analysis, parameter estimation and hypothesis testing. The results show that the vertical and horizontal maximum positive temperature difference of the in-service curved beam bridge of asphalt pavement obeys the two-parameter Weibull distribution. The vertical maximum daily positive temperature difference is 21.7 ℃, the frequency value is 21.4 ℃, and the quasi-permanent value is 20.3 ℃. The horizontal maximum daily temperature difference is 14.1 ℃, the frequency value is 13.7 ℃, and the quasi-permanent value is 12.6 ℃. The standard value of lateral temperature difference accounts for 64.9% of the vertical direction, which provides a basis for the value of temperature in the design calculation of the curved beam bridge in the Central Plains.

curved beam bridge; actual data; temperature difference; cluster analysis; Weibull distribution

10.19713/j.cnki.43−1423/u.T20190810

U442.5

A

1672 − 7029(2020)07 − 1751 − 09

2019−09−10

国家自然科学基金资助项目(50878198)

孙增寿(1963−)，男，河南三门峡人，教授，博士，从事桥梁损伤检测与健康监测研究；E−mail：zengshou@zzu.edu.cn

(编辑 涂鹏)