一种成本有效的面向超参数优化的工作流执行优化方法

姚 艳，曹 健

(1.齐鲁工业大学(山东省科学院) 计算机科学与技术学院,山东 济南 250353；2.上海交通大学 计算机科学与工程系,上海 200240)

0 引言

在大数据时代，借助大数据分析技术，可以对海量数据进行更全面、更快速、更深度、更准确的挖掘分析，从而发挥数据的最大价值，并辅助做出最佳决策[1]。大数据分析的流程一般包含数据收集、预处理、模型学习和模型预测等。其中，模型学习和模型预测两部分是发挥数据最大价值和辅助决策的关键步骤[2]。而机器学习算法是模型学习和预测不可或缺的关键技术之一。同时，机器学习算法可以发现数据的隐含模式，也是使得数据分析自动化的核心技术。

在数据分析过程中，监督式学习算法需要耗费大量的时间来训练和评估数据集，而非监督式学习算法则需要耗费时间来执行数据集。此外，大部分机器学习算法(无论是监督学习还是非监督学习算法)都需要在训练或执行之前对一些变量值进行配置[3]。这些在模型学习开始执行之前设置的变量值(或参数)被称为超参数(hyperparameter)，它们不能从数据中学习，需要预先定义，例如K近邻(K-Nearest Neighbors, KNN )算法中的近邻个数k、神经网络的学习率等。在机器学习算法中，超参数的选择和调优非常重要，不同的超参数值组合将会输出不同的学习性能(准确率(accuracy)、查准率(precision)、召回率(recall)等)。此外，各个超参数对学习模型的影响并不相互独立，且不同的学习模型有不同的最优超参数配置。

超参数的选择对学习模型的效果和运行时间有极大的影响，如何为机器学习算法选择一组好的超参数一直是机器学习领域的难题之一，由此，超参数优化应运而生。超参数优化是一个非常耗时和耗费资源的过程。随着云计算技术的成熟，越来越多的数据分析任务被放在云计算平台中处理。为了充分利用云计算的分布式资源，可以将超参数调优并行化进行[4]。由此引出一个优化问题，在云计算的按需付费机制下，需要寻找一种成本优化的并行超参数调优的执行策略。

目前关于超参数优化的研究，大部分是以学习模型性能为目标[5]，考虑成本开销的研究工作则比较少。本文基于当前的超参数优化方法，在不改变学习模型性能(如准确率、查准率、召回率等)的基础上，考虑如何使得超参数优化执行尽可能快的同时成本开销尽可能低。在笔者前期工作中[6]，针对同构类型的服务器场景，将问题归约为数字分组问题进行求解。本文则考虑不同类型服务器场景下的优化，首先定义了超参数优化工作流，然后将问题转化为构建一个最优的工作流模型的优化问题，并针对异构服务器的情形，提出了双染色装箱算法对问题进行求解。

1 相关工作

1.1 超参数优化方法

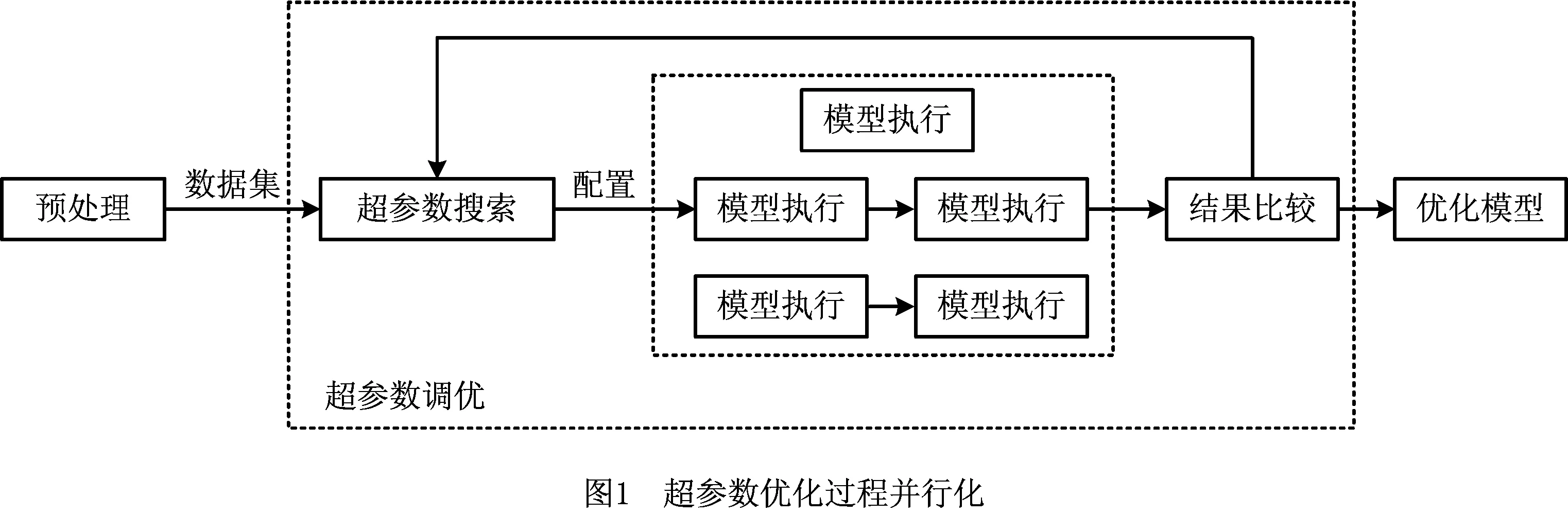
超参数(Hyperparameter)是机器学习模型在运行前需要设置的参数，如决策树算法中的分支最大深度。通常，为学习模型选择较优的超参数可以提高模型性能和效果，这个过程就是超参数优化(hyperparameter tuning、hyperparameter optimization或hyperparameter search)。常见的超参数优化方法有网格搜索[5]、随机搜索[7]、贝叶斯优化方法[8]等。这些自动化调优算法的本质是对超参数值进行不断的试错调整或者优化策略筛选式调整，整个过程可以并行化进行[9]，如图1所示。

1.2 程序运行时间估计

程序的运行时间分析主要分为动态分析技术和静态分析技术[12]。动态分析技术，即基于测量的分析技术，是在目标机器上运行特定的分析程序并统计其运行时间，分析难度低，但是其结果受限于运行环境，无法覆盖所有执行情况；静态分析技术是在不实际执行代码的情况下，对程序执行进行建模分析。

1.3 装箱问题

装箱问题(bin packing problem)是将小物品装入大容器，并使之在一些约束条件下满足特定优化目标(如消耗的容器数量最少、装入的物品总价值最高等目标)的布局优化问题，属于一类NP完全的离散组合优化问题[10]。这里容器和物品都是泛指，容器不仅是箱形的容器，还可以是一段时间、一个空间或一些资源等；同理，物品不仅是物品，还可以是时间碎片、小空间或任务等。

目前，装箱问题有多种分类[11]：根据维数，装箱问题可以划分为一维装箱、二维装箱和三维装箱等;根据优化目标的不同，可以划分为输出价值最大化和输入价值最大化两类；根据对物品的分类，划分为相同物品和异构物品等；根据箱子的不同，划分为固定尺寸的箱子和箱子尺寸可变等优化问题。

2 考虑成本开销的超参数优化问题

2.1 资源模型

本文中的机器学习算法的运行平台是云计算平台。云服务提供商通过虚拟化等技术对云用户屏蔽了底层硬件资源(CPU、内存、存储、网络等)的差异性，将计算资源以虚拟机的形式提供给用户。用户不需要关心任务具体运行的物理服务器的位置，只需根据需求确定虚拟机资源的配置和数量等。目前，大多数云服务提供商(如Amazon的AWS(https://aws.amazon.com/)，Google Cloud(https://cloud.google.com/)，Microsoft Azure(https://azure microsoft com/)，阿里云(https://www.aliyun.com)等)提供多种性能异构的虚拟机实例规格。不同规格的虚拟机不但配置不同，而且价格也互不相同，配置越高的虚拟机，通常价格也越高。

此外，云服务厂商针对虚拟机实例也提供了多种收费机制，常见的收费机制有按需收费、预留收费和竞价收费等。本文研究主要考虑按需收费机制，即对于虚拟机实例按某个单位时间(例如Google以分钟计费，AWS、阿里云等以小时计费)支付计算时长费用。如果不满计费时长则按整计算时长收费。

2.2 问题形式化

机器学习任务taski的执行时间记作ti，则不同的机器学习任务的运行时间是有差异的(即使相同规格的虚拟机，运行时间也可能不同)。换言之，这S个机器学习任务的运行时间有快有慢，而整个调参过程的执行时间是指所有这些机器学习任务完成所花费的时间。

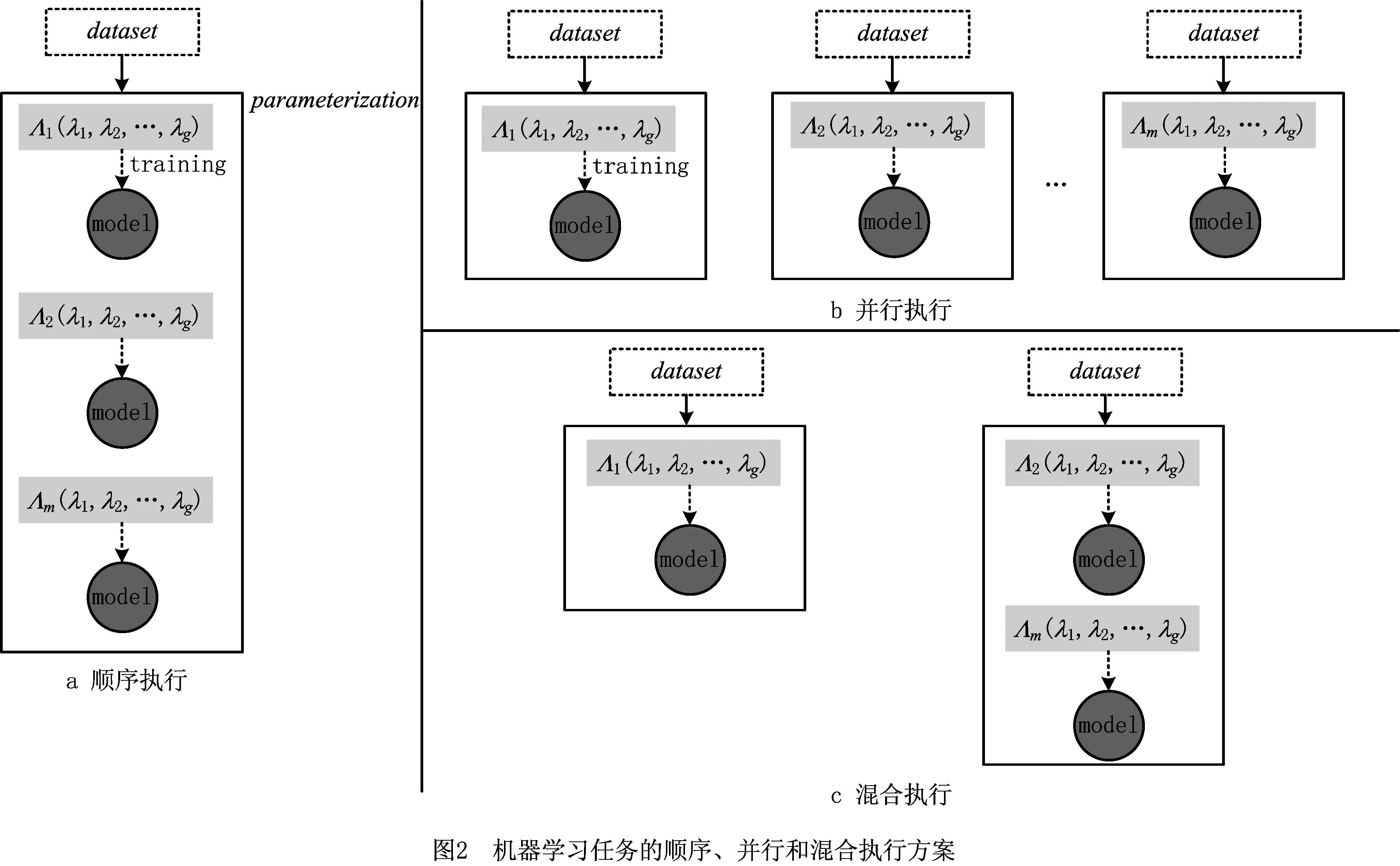
当在云计算平台中运行这些机器学习任务时，存在3种不同类型的执行方案，如图2所示。

(2)第2种执行方案是完全并行执行(如图2b)，每个机器学习任务分配到独立虚拟机上运行，该方案利用云计算平台的分布式特性，其执行时间无疑是速度最快的，由所有机器学习任务的执行时间最慢的任务所决定：Time(Parallel)=max(ti)，但需要租用大量的虚拟机(S台)，从而产生较高的成本。而且如前所述，不同的机器学任务的运行时间有差异，运行速度快的机器学习任务所在的虚拟机会存在较长时间的空闲。

(3)第3种执行方案是将前述的串行和并行两种方案进行混合(如图2c)，将运行速度快的多个机器学习任务放置到同一台虚拟机上串行执行，这样既减少了虚拟机的数量，又不会降低机器学习任务的总执行速度。

显然，第3种混合方式是比较理想的选择，但如何对这些机器学习任务进行组合以及租用什么规格的虚拟机，从而使得整个超参数优化过程最快同时成本尽可能低是一个组合优化问题。

2.3 超参数优化工作流

本文将超参数优化过程中所有机器学习任务的一个执行方案建模为一个超参数优化工作流，则流程中的任务(或者活动)表示机器学习任务，任务之间的依赖关系表示机器学习任务的执行次序。即超参数优化工作流只存在控制流，不存在数据流。同时，还增加了一个起始任务和终止任务，表示数据集的输入和对结果的汇总处理。

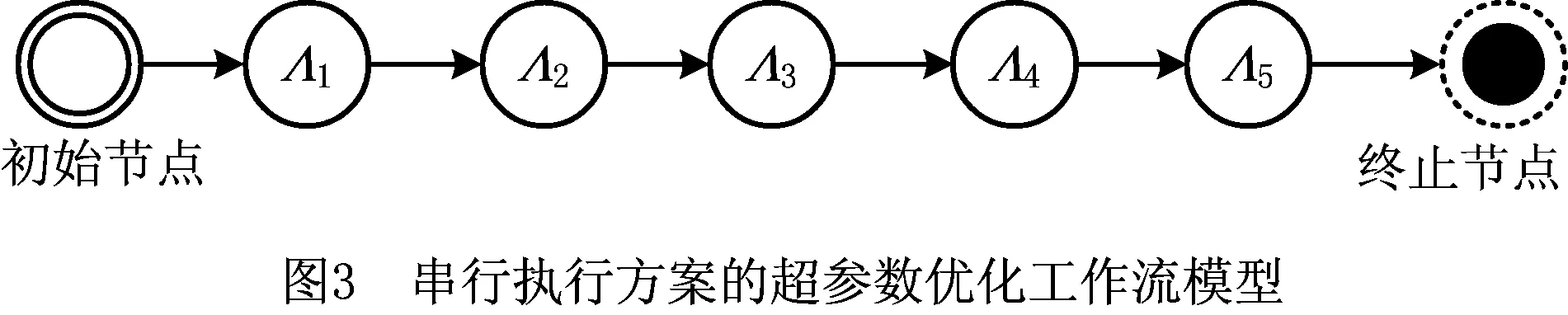
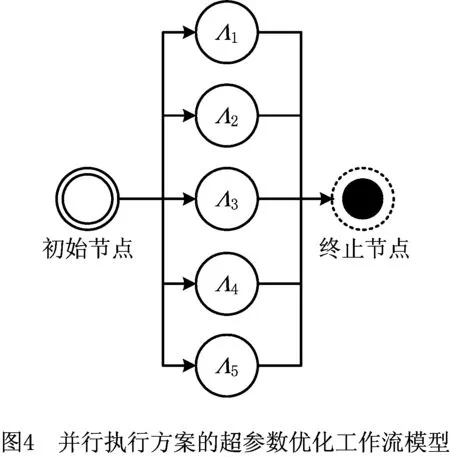
例如，前面的顺序执行方案可以建模为顺序流程，机器学习任务依次执行，如图3所示;并行执行方案可以建模为全并行流程，学习模型之间是相互独立执行，不存在依赖关系，如图4所示。超参数优化过程花费的时间则是超参数优化工作流的完成时间(Makespan)，超参数过程优化问题则转化为构建一个较优结构的超参数优化工作流，使得整个流程的完成时间最短同时费用尽可能地低。

3 超参数优化工作流的任务运行时间估计

在构建模型之前，首先需要对流程中每个任务的运行时间进行预测。一般地，算法的运行时间(或执行时间)需要通过实现该算法的程序代码在服务器上运行时所消耗的时间来进行度量。程序的运行时间一般受到以下几个因素影响:

(1)算法的输入(数据集特征及规模等)。

(2)算法自身采用的策略、方法等。

(3)系统环境(编译器、编程语言、IDE环境、模型库等)。

(4)硬件环境因素(比如CPU型号、内存、机器执行指令的速度等)。

抛开与计算机硬件、软件有关的因素，一个程序的运行时间依赖于算法的自身和问题的输入规模。因此，本文主要从算法自身和输入规模两方面来探索利用时间复杂度函数对超参数优化工作流中的任务运行时间进行估计。

维基百科中给出算法时间复杂度的定义：在计算机科学中，算法的时间复杂度(time complexity)[13]是一个函数，定量描述了该算法的运行时间。时间复杂度是一个关于代表算法输入值的字符串的长度的函数，常用O表述，不包括这个函数的低阶项和首项系数，

T(n)=O(f(n))。

(1)

式中：T(n)表示算法的时间复杂度，f(n)表示执行与算法自身和问题规模n有关的执行数。

机器学习算法的时间复杂度除了与数据集规模有关外，还与超参数值的选择有关。对于超参数优化工作流中的所有任务，其数据规模相同，区别在于超参数的取值。根据时间复杂度函数大胆推论:固定数据规模，可以认为机器学习算法的执行时间与超参数组合之间是线性关系如下：

Time(MLTask)=αC+β。

(2)

式中：C表示学习算法的超参数组合，α和β需要根据软硬件环境和数据集进行拟合得到。式(2)中α和β的取值可以根据不同的服务器和数据集进行线性拟合。具体的实验验证可以参考笔者以前的工作[11]，这里不作详细阐述。

对于神经网络类的算法，实际运行时间高度依赖于具体的实现，其时间复杂度函数也较复杂，估计运行时间与实际运行时间之间的误差可能相对较大。例如在卷积神经网络中，标准卷积和分组卷积的时间复杂度相同，但是分组卷积的内存访问开销更大，相同数据规模下，分组卷积的实际运行时间会比标准卷积长。但因为笔者采用的是最坏时间，所以对结果影响较小。

4 超参数优化工作流模型构建算法

4.1 时间的上下界

已知一组任务规格不同的虚拟机上的估计运行时间，可以计算出超参数优化工作流的完成时间和成本开销的上下界。完成这组任务所需要的最长时间(即运行时间的上界，Timeub)是所有任务在同一台最小规格的虚拟机上顺序执行，如式(3)所示：

(3)

完成这组任务所需要的最快时间(即运行时间的下界，Timelb)是所有任务完全并行的运行在最高规格的虚拟机上，如式(4)所示：

Timelb=maxall(timei,vm.largest)。

(4)

4.2双染色装箱算法DCBP

假设有k种不同规格的虚拟机VM={vm1,vm2,…,vmk}，共n个任务Task={task1,task2,…,taskn}。最慢完成时间记作D，D=Timelb，则问题归约为有色装箱问题。

(1)有色装箱问题 给定N个物品序列Item={item,item2,…,itemN}，物品itemi的大小为size(itemi)，颜色为colorj,j∈[1,k],k表示颜色的种类数。箱子的容积为sizecapacity，箱子个数不受限。现在要求每个物品itemi只能装入唯一的箱子内，且每个箱子内所装物品大小总和不超过箱子的容积，同一个箱子内物品的颜色也必须互不相同，有色装箱问题则是问至少需要多少个箱子才能装下所有物品。

将虚拟机VM看作是箱子，箱子的容量为最慢完成时间D。任务则看作物品，任务的运行时间为物品的大小。物品的颜色为其所分配的虚拟机的类型，因此颜色的总数为虚拟机的类型数。每个物品可以有k种候选颜色可染，每种颜色对应不同size。这里，将每个任务在每种类型虚拟机上的映射看作一个物品，则物品总数为N=n×k。进一步，将这些物品分成n组，每组内的物品是同一个任务，但颜色不同。每个箱子也有k种候选颜色，分别对应不同的费用。目标要求是：每个箱子内所放物品的大小总和不能超过箱子的容量，且每个箱子内所放置的物品的颜色要相同，且物品不全放置，每组内必须选且仅选一个物品。目标是使箱子的费用总和最小。在本问题中，物品和箱子都要染色，因此本文将算法命名为双染色装箱算法(Dual-Colored Bin Packing，DCBP)。与有色装箱问题中的只有物品染色相比，双染色问题要更复杂更难解一些。

算法1Dual-Colored Bin Packing Algorithm(DCBP)。

Require:1)K:VM types;

2)task[n]:n tasks of hyperparameter optimization workflow;

3)D:the deadline of the workflow execution.

Ensure:vm[]:the rented VMs;

mapping[][]:the mapping between tasks and VMs.

1:Initialize vm[].colore←null,vm[].capacity←D;

2:Initialize time[n][K];

3:Initialize mapping[task][]←null;

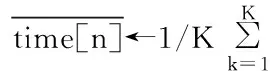
5:Initialize the PPR array PPR[n][K]←(price(colorj)/μ(taski,colorj));%PPR is the best price-performance ratio, the lower PPR, the better

6:Sort the average time in decease order timeSorted[];

7：int j←0;

8:for i=1:i≤n;i++ do

9: taskID←timeSorted[i];

10： color←max(PPR[taskID][K]);

11: if there exist VM with vm[j].capacity≥time[takeID][color]&vm[j].color==color them

12: select the with smallest capacity v[min];

13: assign task[taskID]to the vm[min];

14: vm[min].capacity←vm[min].capacity-time[taskID][color];

15: else%Rent new VM with color type:

16: j←j+1;

17: vm[j].color←color;

18: vm[j].capacity=D;

19: assign task[taskID]to the vm[j];

20: vm[j].capacity←vm[j].capacity-time[taskID][color];

21: end if

22:end for

23.return vm and mapping;

由于所有物品在每种规格虚拟机上的平均运行时间已知，离线算法更合适。本文提出的启发式算法伪代码如算法1所示。算法的基本思想是：首先将所有任务依照平均运行时间排序，然后对队列中的任务依次进行分配。对已出队列的任务，选取使其性价比最好的虚拟机类型进行分配。性价比记作ppr((best price-performance ratio)，

(5)

式中：ppr(taski,vmj)表示任务taski在vmj类型虚拟机数运行时的性价比；vmj.price是vmj类型虚拟机的价格；μ(taski,vmj)表示执行速率。ppr取值越小，性价比越高。

确定虚拟机类型后，决定具体分配到哪台虚拟机时，原则是在所有选定的虚拟机类型的虚拟机中，选择剩余容量最小的那台。如果不存在确定类型的虚拟机，则租用一台新的，直到所有任务全部分配完成。

(2)算法复杂度分析 因为算法的每一个步骤都处理一个物品，而物品总数为N=n×k,，其中n是机器学习任务的个数，k是虚拟机的规格数，所以DCBP算法的时间复杂度为O(nk)。

5 实验及结果分析

5.1 实验设置

本文采用阿里云作为实验平台。以中国大陆区域为例，选取通用型(g5)的按量付费实例类型，CPU类型为Intel Skylake Xeon Platinum 8163，主频是2.5 GHz，具体配置如表1所示。值得注意的是，这里单价是指每小时的价格，但是计价周期是min。例如ecs.g5.large类型的虚拟机的价格为0.89元/h，但阿里云服务提供商对ecs.g5.large以min为单位计费，不足1 min按1 min收费。

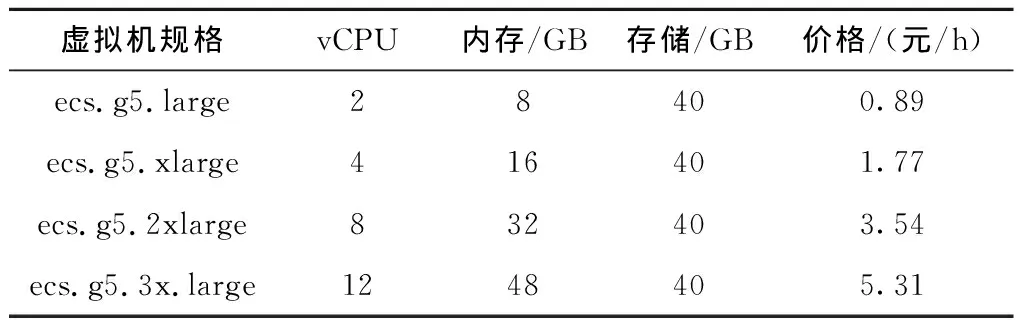
表1 阿里云上中国大陆地域的通用型虚拟机实例规格配置信息

数据集采用MNIST6，分别在4种g5虚拟机实例上进行训练，并拟合出在每种类型虚拟机实例上的模型训练时间估计函数。以K-means为例，拟合出它在4种类型虚拟机上的运行时间与超参数组合之间的时间估计函数。然后配置不同的超参数，获得不同的机器学习任务的估计运行时间。通过生成不同的机器学习任务，对所提出的DCBP算法进行性能评估。以如下的基本调度算法和贪心算法两种策略作为对比：

(1)基本调度(Basic Scheduling，BS)算法 所生成的工作流任务全部并行执行，即每个工作流任务分配一个云服务器。因为这里的云服务器是异构的，实验中有4种不同规格的云服务器，因此，初始调度算法相应的有4种，分别命名为BS1,BS2,BS3,BS4。

(2)贪心算法(Greedy Algorithm，GA) 对于生成的机器学习作流任务，按照运行时间降序排列，然后遍历虚拟机实例，将任务分配到配置较高且能放下的虚拟机，如果同时存在多个相同较高配置的虚拟机实例，则优先选择剩余容量较小的虚拟机实例，否则申请新的虚拟机实例。

5.2 结果分析

通过调整K-means算法超参数的范围，生成不同数量的任务，总数从30～600，分析算法给出的虚拟机个数以及相应的类型(如图5)和总成本开销(如图6)。

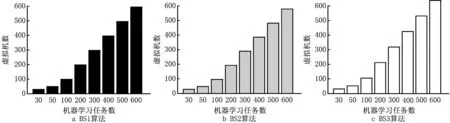
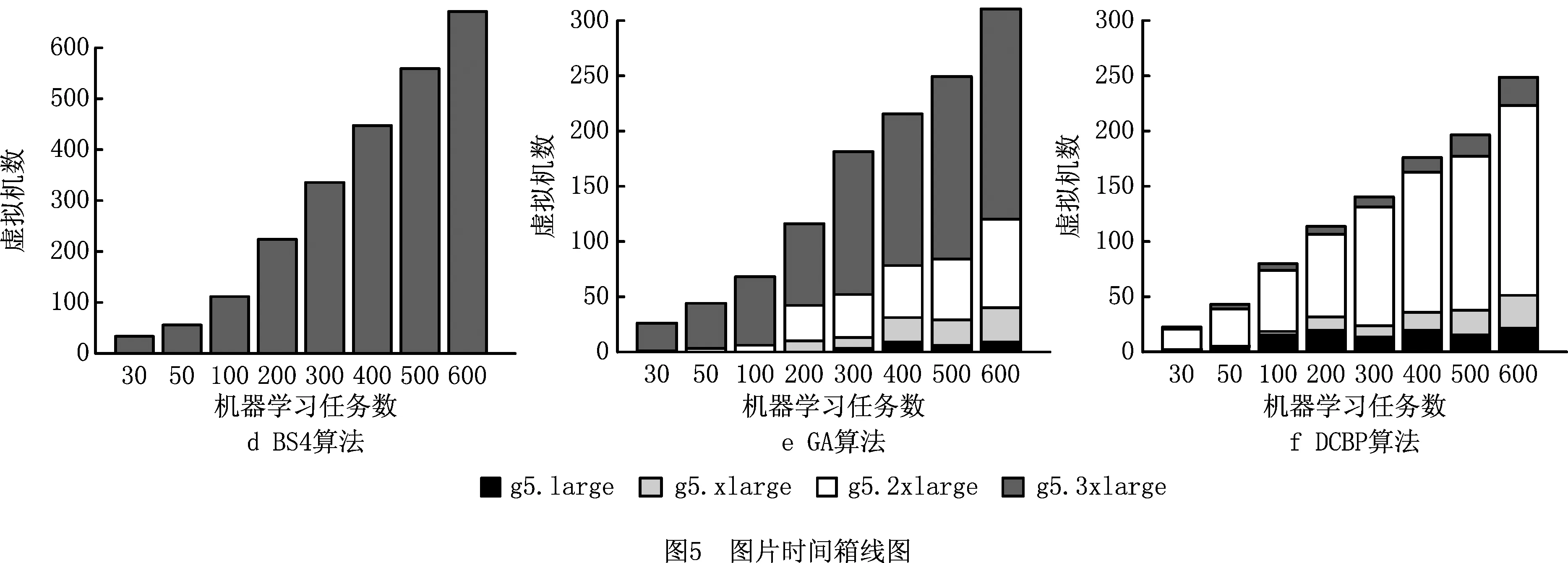
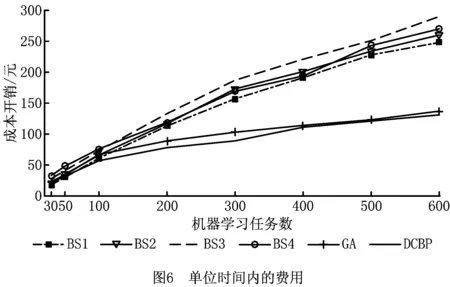
图5展示了不同任务数下的虚拟机情况，BS1、BS2、BS3、BS4算法是全部租用相同类型规格的虚拟机且完全并行，随着任务数量的增长，虚拟机数量呈指数增长。DCBP算法和遗传算法(GA)所租用的虚拟机数量明显少得多，而DCBP算法比GA的虚拟机数量还要少一些。

图5展示了不同任务数下各个算法产生的结果的成本开销虚情况，成本计算如式(6)所示：

(6)

需要注意的是，不同任务下的最佳完成时间是有所差异的(makespan)，如BS4算法采用的是最高配置的虚拟机，因此其完成时间要比采用最低配置虚拟机的BS1算法要快。总体来讲，任务数目越多，所有任务的完成时间越长。可以看出，DCBP算法的资源租用方案费用最少，且在任务数目越多时优势越明显。

6 结束语

本文研究了在云计算平台中，针对机器学习算法的超参数优化的并行执行优化问题。定义每个超参数赋值的机器学习模型为一个机器学习任务，超参数优化的并行执行本质是将这些机器学习任务进行并行处理。现实中，大多数云服务提供商提供多种不同配置的虚拟机规格，不同规格类型的虚拟机执行同一机器学习任务的速率不同，且不同机器学习任务即使在同一个类型虚拟机数的运行时间也不同。因此，在云计算的按需计价模型下，如何将这些机器学习任务进行组合，使得超参数优化过程尽可能快，且成本开销尽可能低是一个组合优化问题。本文提出了超参数优化工作流的概念，并将问题归约为构建一个好的超参数工作流模型的优化问题。然后提出了有色装箱启发式算法对问题进行求解，实验结果表明本文提出的算法可以减少成本开销。未来可以对优化算法进行改进，提出时间复杂度更低且更接近最优解的算法。