基于结构关系的过程模型推荐方法
王华清,夏 鑫,闻立杰+,邱泓钧,王建民
(1.清华大学 软件学院,北京 100084;2.浪潮通用软件有限公司,山东 济南 250101)
1 问题的描述
过程模型用于在一个组织中有逻辑地关联起各个任务,从而实现业务目标,描述业务过程行为。分析人员在许多情况下手动构建业务过程模型,用以捕获业务需求并在业务过程分析人员和计算机专家之间建立沟通渠道。尽管如此,人工构建业务过程模型依然耗时且容易出错。因此,需要一种过程模型推荐方法来提高业务过程模型建模的正确率和效率。
虽然业务过程模型推荐方法已经用于学术研究和工业过程中,但这仍然是一个相对较新的领域。目前只有少量的业务过程模型推荐方法[1-6],而这些方法有3个主要问题:
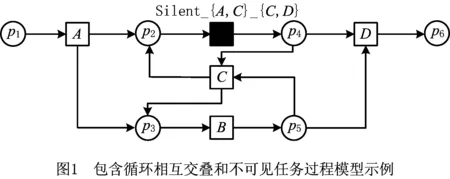
(1)无法处理复杂结构,如图1所示循环相互交叠的情况(即B和C,以及Silent_{A,C}_{C,D}和C)。另外,它们也无法处理带有不可见任务的模型,如图1中的Silent_{A,C}_{C,D}。本文4.1节将介绍不可见任务的打标规则和使用方法。
(2)不能处理具有大量过程模型和活动节点的复杂大数据集。在这些大数据集中,同一个活动节点可能出现在大量不同的模型中,与其他活动节点以复杂的形式相连接。
(3)正确率和效率不足以满足实际应用的要求,仍有很大的提升空间。
为解决以上问题,本文提出一种基于前驱活动序列和后继活动节点之间结构关系的过程模型推荐方法。该方法能记录过程模型中可能存在的活动序列信息,并且可以将并不直接相连,但是在同一活动序列中的活动节点相互关联起来。本文的贡献在于:
(1)提出了一种基于前驱活动序列和后继活动节点之间结构关系的过程模型推荐方法,能够高效准确地进行过程模型推荐,并且能够处理复杂结构、不可见任务和大数据集。
(2)提出了一种对不可见任务进行打标的方法,使其能够与可见任务一样被推荐方法推荐。
(3)提出了一种前驱活动序列和后继活动节点之间结构关系的提取算法。
(4)通过大量实验证明了本文的方法在所有数据集上全面优于其他已有方法。
2 相关工作
业务过程模型推荐方法通过推荐一组候选活动节点作为未完成模型的下一个活动节点的选项来帮助用户构建未完成的模型。目前只有少量的业务过程模型推荐方法,这些方法的对比信息如表1所示。
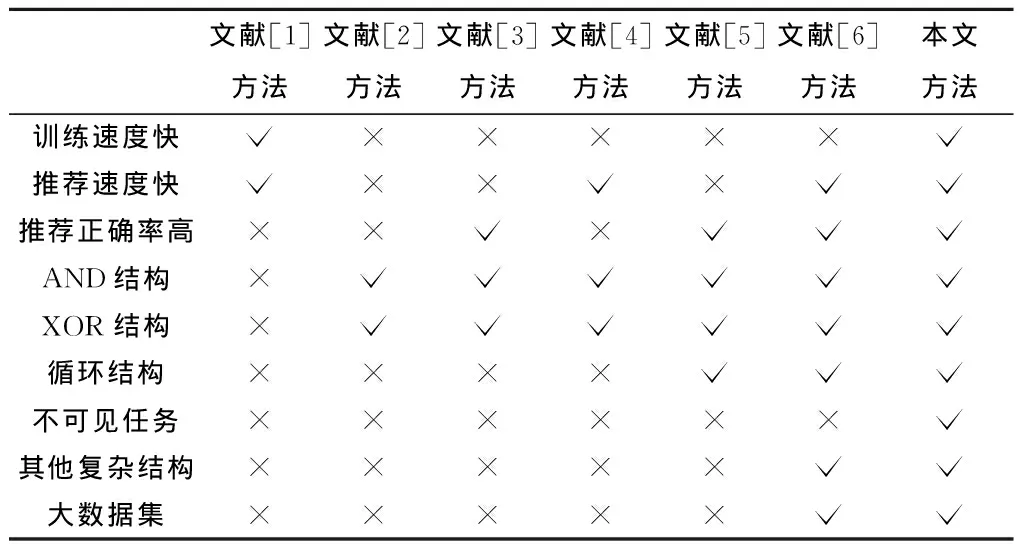
表1 业务过程模型推荐方法对比
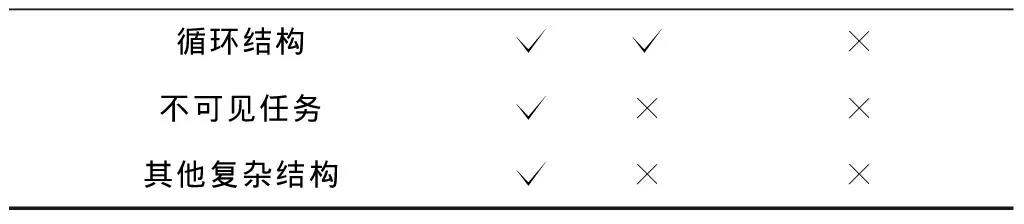
文献[1]提出的FlowRecommender推荐系统基于现有过程模型中活动节点之间的关系来进行推荐。然而,该方法只能支持因果关系。文献[2]使用图挖掘算法提取了过程模型中的所有子图结构,并通过计算图编辑距离来推荐候选活动节点列表。然而,计算图编辑距离问题是一个NP困难问题,这导致了极高的时间复杂度,且该方法不能处理过程模型中的循环结构。文献[3]使用最大公共子图搜索算法替代了图编辑距离。然而,最大公共子图搜索算法也是NP困难问题,且该方法仍然无法处理循环结构。文献[4]将图编辑距离问题转换为字符串编辑距离问题,然而,该方法仍然不支持循环结构,且在一定程度上会降低推荐的精度。文献[5]提出3种新的距离函数,分别是最大最小公共子图距离(Maximal and minimal Common Subgraph Distance, MCSD)、修正图编辑距离(extended Graph Edit Distance, xGED)和修正字符串编辑距离(extended String Edit Distance, xSED)。但是,这些方法仍然不能推荐复杂结构,如循环相互交叠的情况和不可见任务。另外,这3种策略依然无法处理大型复杂数据集。文献[6]提出的RLRecommender方法用表示学习的方法将活动节点映射到多维空间中进行推荐。但是,该方法的正确率和效率有很大的提升空间。
本文所提出的方法需要提取活动节点之间的关系来获得业务过程的结构信息,下面给出一些业务过程模型活动节点关系提取算法的相关工作,如表2所示为这些方法的对比信息。
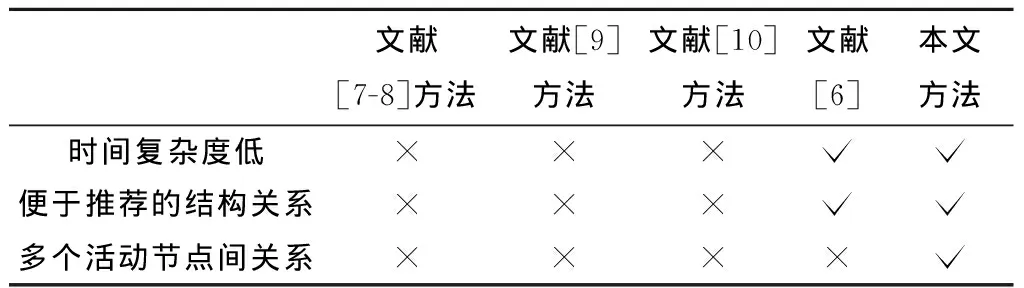
表2 活动节点关系提取算法对比
文献[7]提出了行为轮廓(Behavioral Profile, BP),并在文献[8]中对其进行了扩展,提出了一组过程模型中两个活动节点之间的基本行为关系,包括严格顺序关系、互斥关系和交叉顺序关系。然而,该方法关注的是每对活动节点之间的行为关系,而非结构关系。文献[9]基于活动间的次序关系提出了4C Spectrum,包括各种共存、冲突、因果和并发关系。然而,4C Spectrum各种关系互相之间的组合过于复杂,难以用统一的算法进行处理。文献[10]提出了扩展精细不确定次序关系(Extended Refined Ordering Relations with Uncertainty, ExRORU),使用因果关系、反向因果关系和并发关系的组合来描述活动节点之间的行为。然而,这种方法并不关注相互连接部分活动节点之间的直接关系。文献[6]提出了可用于推荐方法的关系提前策略,包括直接连接、直接因果和直接并非关系。但该方法仅考虑了两个活动节点之间的关系,而不考虑活动序列在推荐问题中的应用。
3 预备知识
本文的推荐方法将以合理工作流网的形式处理业务过程。合理工作流网是特殊的Petri网,而Petri网既能够精确地表达各种过程模型结构,又具有表达简单便于处理的特性。首先给出Petri网、工作流网和工作流网合理性的定义。
定义1Petri网。一个Petri网N是一个三元组(P,T,F),其中:P为有限的库所集合;T为有限的变迁集合,且P∪T≠∅∧P∩T=∅;F⊆(P×T)∪(T×P),为有向边集合(即流关系);对于任意节点x∈P∪T,·x={y|(y,x)∈F},x·={y|(x,y)∈F}。
定义2工作流网。一个Petri网N=(P,T,F)是一个工作流网,当且仅当下列条件同时成立:
(1)有且仅有一个输入库所i∈P(源库所)满足·i=∅。
(2)有且仅有一个输出库所o∈P(汇库所)满足o·=∅。
(3)任意节点x∈P∪T都在源库所到汇库所的某一条路径上。
定义3工作流网合理性。在一个工作流网N=(P,T,F)中,i是源库所且o是汇库所。N是合理的,当且仅当下列条件同时成立:
(1)从i拥有唯一托肯的状态出发,在经过执行后必定能到达o拥有唯一托肯的状态。
(2)对任意变迁t∈T,从i拥有唯一托肯的状态出发,总有一种执行方法使得t能够被执行。
图1是一个简单的工作流网,p1、p2、p3、p4、p5和p6是库所;A、B、C、D和一个不可见任务是变迁。工作流网是Petri网的一个子集,用于表示工作流。如果一个工作流网在任何执行顺序下都可以正常终止,同时该工作流网不包含无法执行的变迁、死锁和活锁,则该工作流网便是合理的。图1中的Petri网就是一个合理工作流网。每个可见的变迁表示一个活动,不可见任务则可以用来表示许多结构。活动标签和不可见任务定义如下。
定义4标签工作流网和不可见任务。一个标签工作流网NL是一个三元组(N,L,fL),其中:N=(P,T,F)为一个合理工作流网;L={l1,l2,…,l|L|}为标签集合;fL:T→L∪{τ}为一个标签函数,它会给每个变迁一个标签(τ是空标签);变迁t是不可见任务,当且仅当fL(t)=τ。
在图1中,每个活动的名称就是可见变迁的标签,即A、B、C和D,它们不为空标签,且在工作流网的执行过程中会被用户观察到。在图1中,没有活动名称的变迁是一个不可见任务,且在执行该合理工作流网时,用户不会观察到此变迁所代表的任务被触发。
4 基于前驱活动序列和后继活动节点之间结构关系的推荐方法
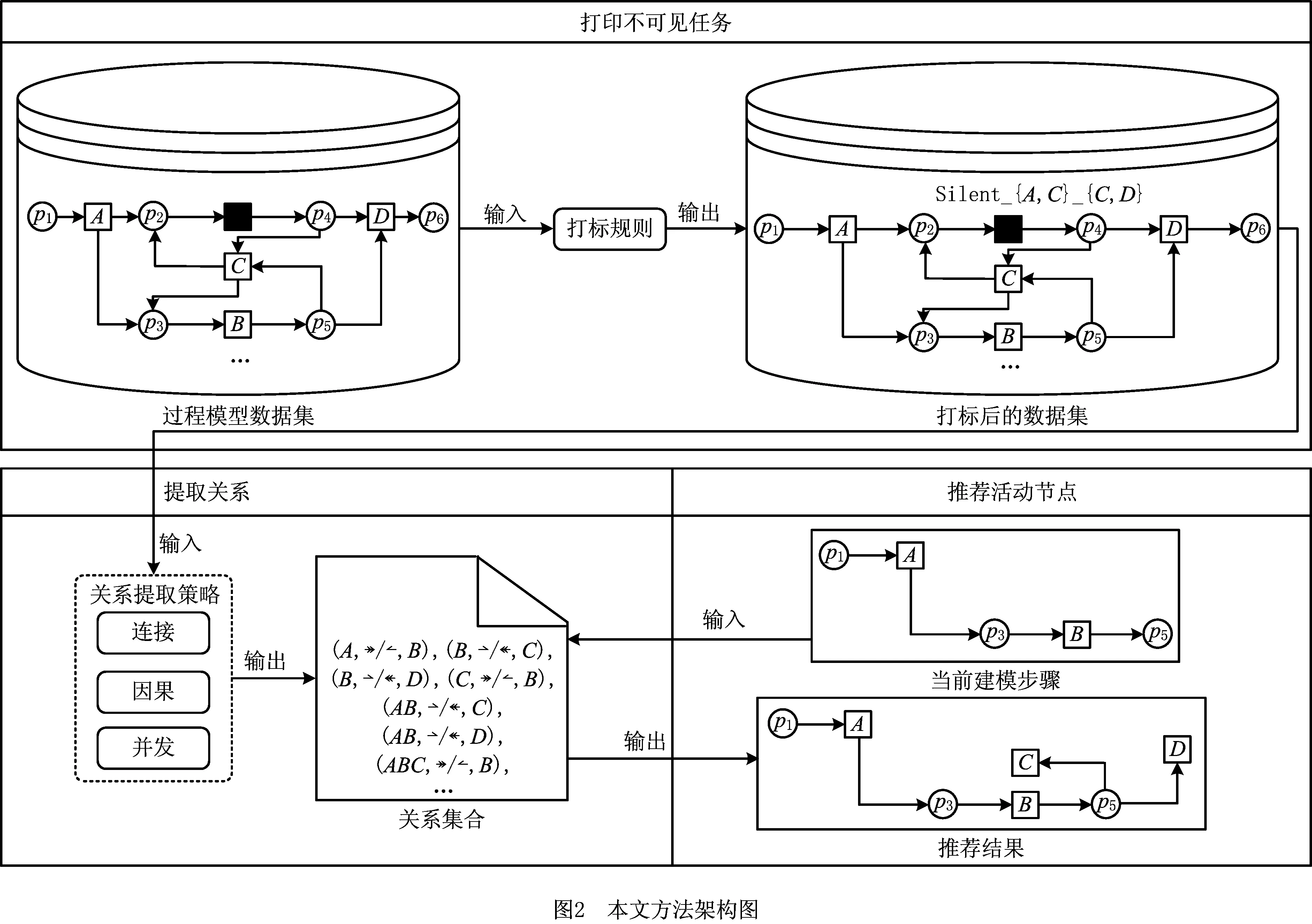
本文提出的基于前驱活动序列和后继活动节点之间结构关系的推荐方法由打标不可见任务、提取关系和推荐活动节点3个阶段组成,如图2所示。
4.1 打标不可见任务
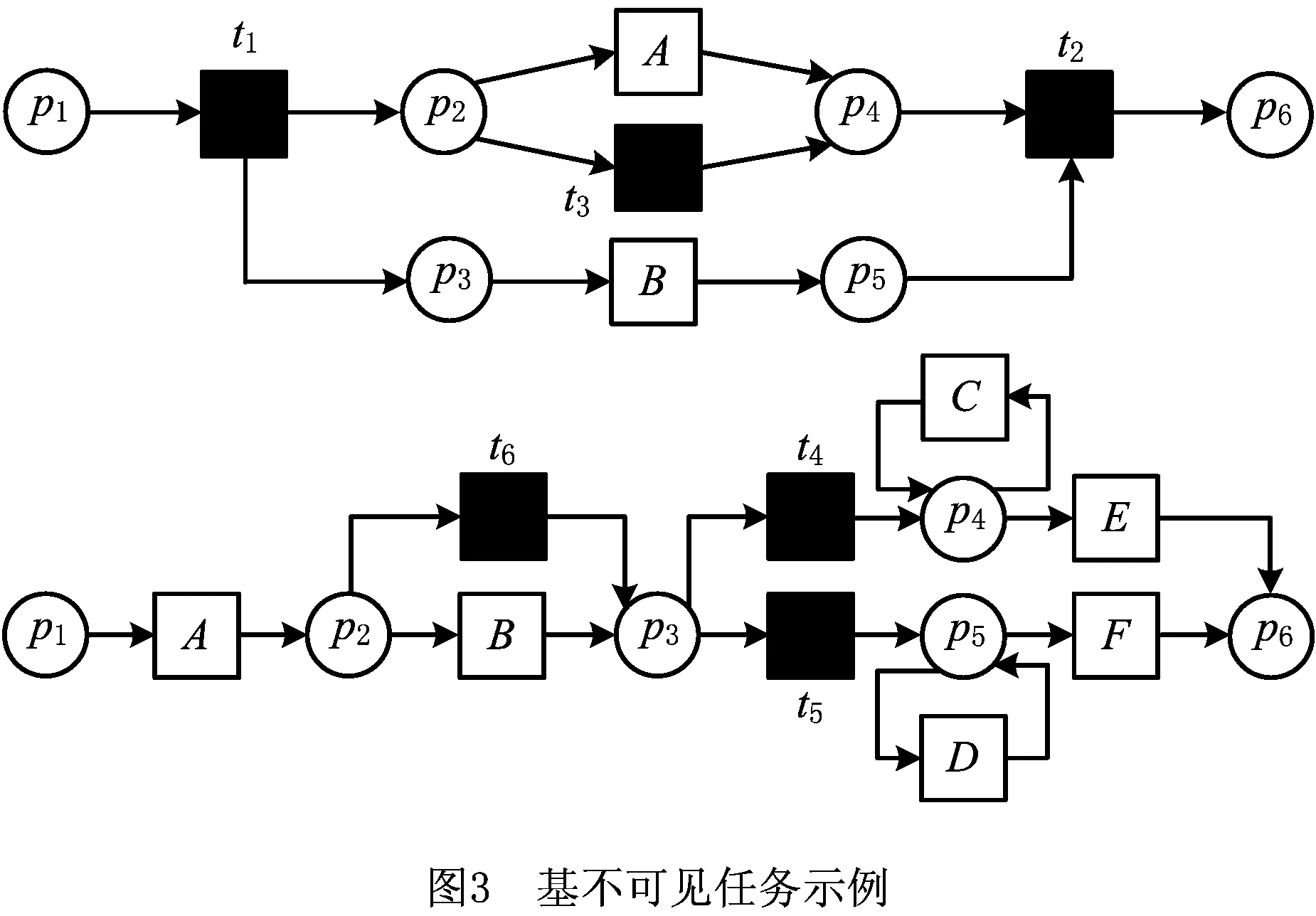
过程模型中的不可见任务没有活动名称,因此需要对它们进行打标,以便将它们与可见的活动节点一并进行处理。在打标不可见任务之前,需要确保数据集中所有不可见任务都是基不可见任务,从而获得记录其结构信息的正确标签。基不可见任务的定义如下。
定义5基不可见任务。在一个合理工作流网N=(P,T,F)中Ts={ts|ts∈T∧ts不可见},i是源库所并且o是汇库所。不可见任务ts∈Ts是基不可见任务,当且仅当下列条件同时成立:
(1)(i∈·ts)∨(((∀p∈·ts,|·p|>1)∨(∃(p,ts),(t,p)⊆F,s.t.(t∉Ts)∨(i∈·t)))∧(∃(p,ts)∈F,s.t.|p·|>1));
(2)(o∈ts·)∨(((∀p∈ts·,|p·|>1)∨(∃(ts,p),(p,t)⊆F,s.t.(t∉Ts)∨(o∈t·)))∧(∃(ts,p)∈F,s.t.|·p|>1));
(4)·ts∩ts·=∅;
(5)ts∉i·∩·o。
图3给出了基不可见任务的一些示例。在图4中,t1和t2分别与源库所和汇库所相连,即它们分别是起始变迁与结束变迁,因此它们都是基不可见任务;t3输入库所之前有起始变迁,输出库所之后有结束变迁,同时其在输入输出库所与A争抢托肯,因此t3也是基不可见任务;t4和t5输入库所之前有可见任务B,输出库所之后分别有可见任务E和F,同时它们在输入库所互相争抢托肯,在输出库所分别与C和D争抢托肯,因此t4和t5也是基不可见任务;t6入库所之前有可见任务A,所有输出库所之后都有至少两个不可见变迁,同时其在输入输出库所与B争抢托肯,因此t6也是基不可见任务。
为消除非基不可见任务,这里给出一些消除规则,如图4所示。图4a消除了在其输入库所没有其他变迁与其争抢托肯的不可见任务。图4b消除了在其输出库所没有其他变迁与其争抢托肯的不可见任务。图4c将相同的不可见任务进行了合并。图4d消除了不可见任务自循环的情况。另外,使用图4中的消除规则后,合理工作流网中的所有不可见任务一定是基不可见任务,下面给出该定理及其证明。
定理1在合理工作流网N=(P,T,F),Ts={ts|ts∈T∧ts不可见},i是源库所且o是汇库所。使用图4中的消除规则后,所有不可见任务一定是基不可见任务。
证明这里通过反证法进行证明。

另外有(i∉·ts)∧(o∉ts·),即ts不是起始或结束变迁;否则,由定义5中的第1个或第2个条件,ts是基不可见任务,这与ts不是基不可见任务的假设相矛盾。
另外还可以得到·ts∩ts·=∅,即定义5中的第4个条件成立;否则,ts可以被图4d中的规则消除。
此外还可以得到∃p1,p2∈P,p1≠p2,s.t.(p1,ts)∈F∧|p1·|>1∧(ts,p2)∈F∧|·p2|>1;否则,ts可以被图4a或图4b中的规则消除。
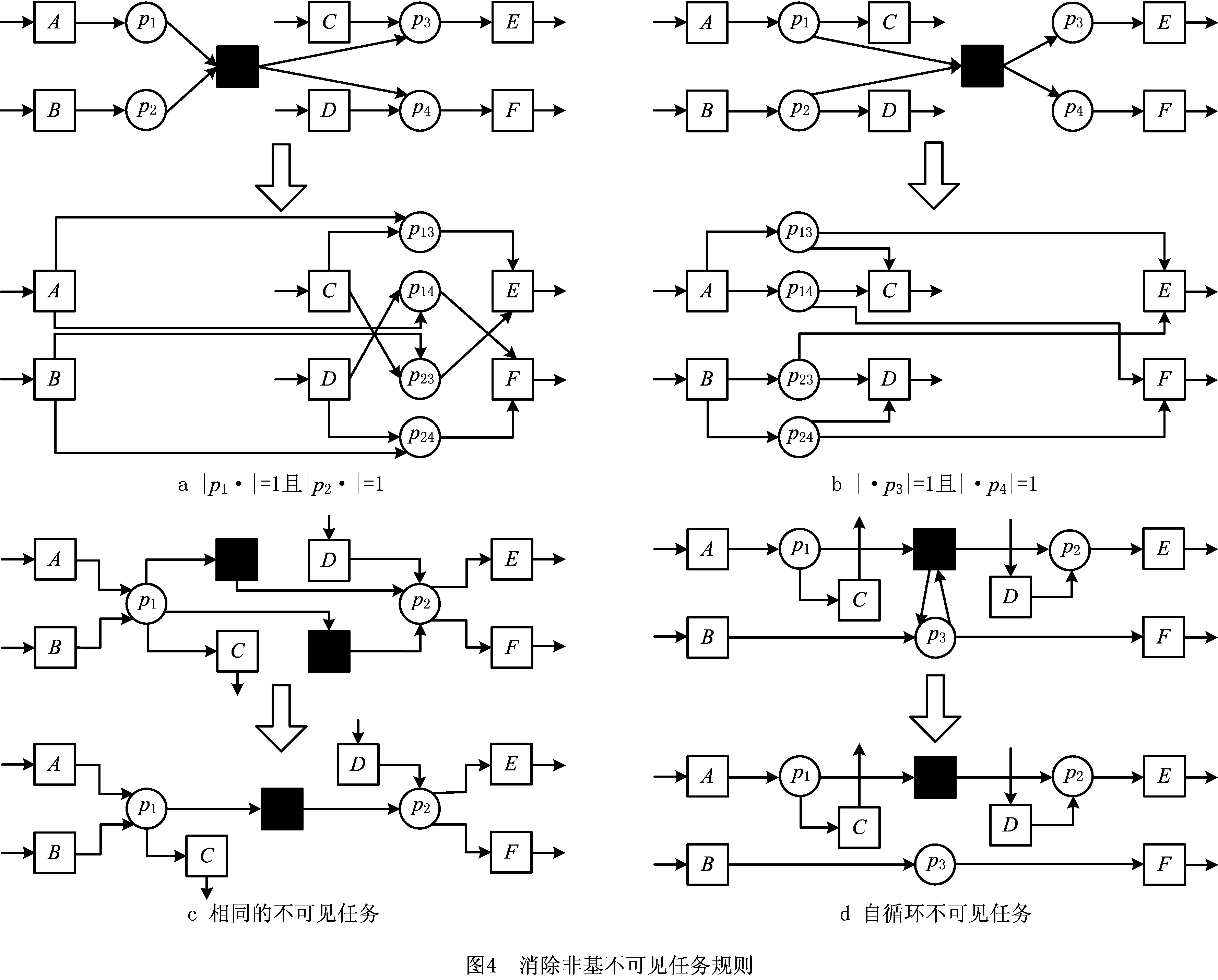
因此,可以推出(∀{(p,ts),(t,p)}⊆F,(t∈Ts)∧(i∉·t)或(∀{(ts,p),(p,t)}⊆F,(t∈Ts)∧(o∉t·)。假设ts没有输出的可见活动节点或结束变迁(即(∀{(ts,p),(p,t)}⊆F,(t∈Ts)∧(o∉t·)),另一种情况的证明相似。
由于ts不是基不可见任务,因此∃p∈ts·,s.t.p·={t}∧t∈Ts。因为t同样无法被消除且ts没有输出的可见活动节点或结束变迁,所以有∃p′∈·t,s.t.∃t′∈p′·,t′≠t,如图5所示。
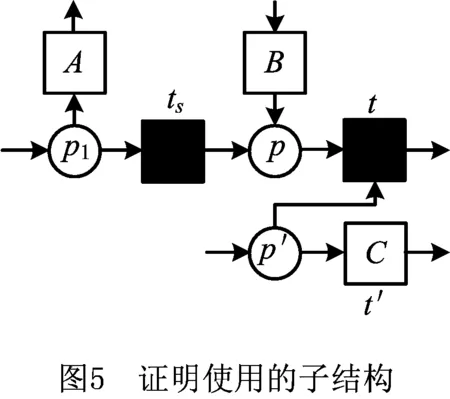
但是,在图5的子结构中,如果t′在执行时从p′中获取托肯,则t将无法被触发且p中的托肯将无法被消耗,即该子结构不会出现在合理工作流网中。这与证明开始的假设相矛盾。
因此,所有不可见任务在使用消除规则后都是基不可见任务。
定理1表明在进行消除之后,所有不可见任务一定都是基不可见任务,这意味着对于每个基不可见任务,可以给出记录其结构信息的适当标签。
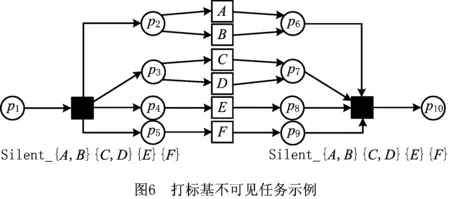
每个不可见任务的打标规则由两部分组成。首先,使用“Silent_”作为新标签的前缀,然后加上其所有输入库所对应的字符串,字符串用输入库所的输入可见活动节点标签集合表示。其次,将第一步得到的结构与“_”相连接,并在后面加上其所有输出库所对应的字符串,字符串用输出库所的输出可见活动节点标签集合表示。新标签中的输入和输出可见活动节点的标签按字典顺序排列。
若基不可见任务具有多个输入或输出库所,则这些库所对应的输入和输出可见活动节点的标签需要按输入和输出库所进行分组,且所有组的字符串之间都需要按字典顺序排列;如果输入库所没有输入可见活动节点,或者输出库所没有输出可见活动节点,则该输入或输出库所不会出现在不可见任务的标签中。
如图6所示为打标基不可见任务的示例,图中的两个基不可见任务都用其输入输出库所对应的可见活动节点标签进行了打标。
推荐完成后,完成的过程模型中所有变迁都将有一个标签,可以是可见活动节点的活动名称,也可以是不可见任务以“Silent_”开头的标签。只需要将标签以“Silent_”开头的变迁转换回不可见任务,就可以正确推荐不可见任务并构建正确的过程模型。
令ns和xs分别表示一个过程模型中不可见任务的数量和单个不可见任务的输入或输出边数的最大值。对于每个不可见任务,需要遍历其所有与可见活动节点相连接的输入和输出边,并消除该不可见任务或对其进行打标。因此,打标一个过程模型中不可见任务的时间复杂度是O(nsxs)。
4.2 提取关系
本节从过程模型中提取前驱活动序列和后继活动节点之间的关系。得到的关系集合将在提取后被储存在后端,因此每个过程模型只需提取一次关系即可。关系提取算法的第一个策略(即k连接策略)仅使用“直接k连接”关系。“直接k连接”关系的定义如下。
定义6直接k连接。在一个合理工作流网N=(P,T,F)中:
(1)变迁x,y∈T为“直接1连接”关系(x→y)⟺∃p∈x·,使得y∈p·;
(2)变迁x1,x2,…,xk,y∈T为“直接k连接”关系(x1x2…xk→y)⟺x1→x2∧x2→x3∧…∧xk-1→xk∧xk→y。
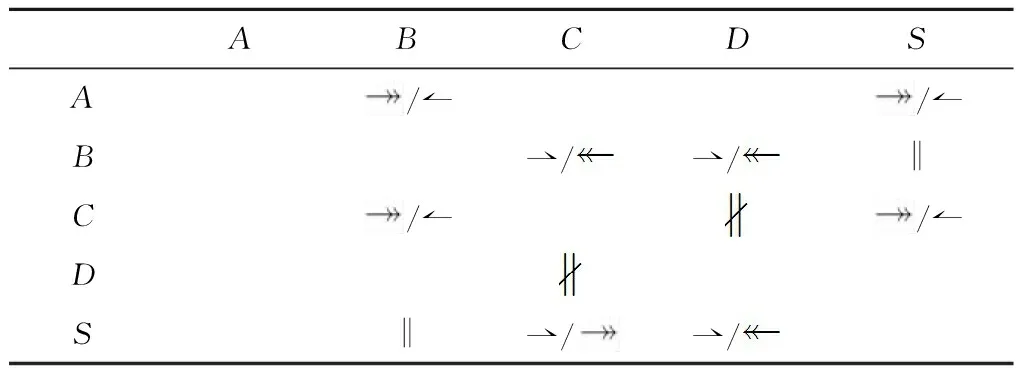
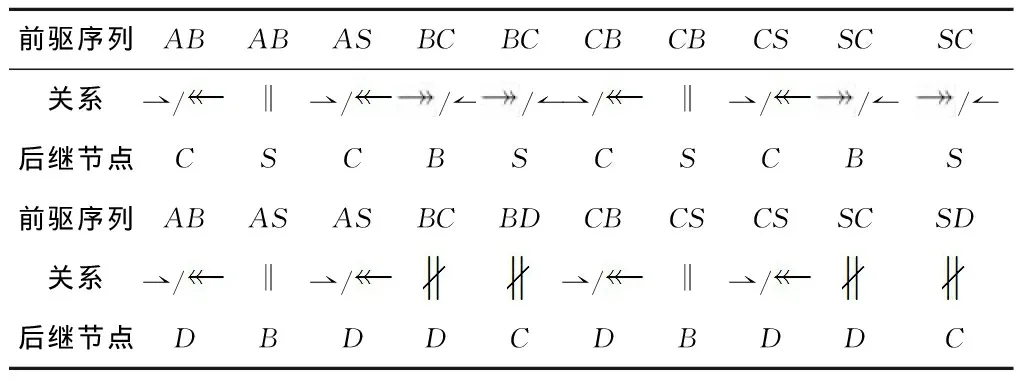
“直接k连接”关系能够描述合理工作流网中所有可能的活动序列连接关系,从而提取出业务过程模型在执行过程中的结构信息。例如图1中的过程模型中,在不同k值下可以得到A→B和AB→C。
在提取“直接k连接”关系时,需要对每个节点用深度优先搜索寻找该节点所有长度为k的前驱活动序列。因此,从一个过程模型中提取“直接k连接”关系的时间复杂度是O(nxk),其中n和x分别表示一个过程模型的节点数和单个节点输出边数的最大值。
但是,“直接k连接”关系无法区分AND结构和XOR结构之间的区别。因此,关系提取算法的第2个策略(即k因果策略)使用“直接k因果”关系和“反向直接k因果”关系的组合。两种“直接k因果”关系的定义如下。
定义7总是/有时直接k因果。在一个合理工作流网N=(P,T,F)中:
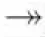
(2)变迁x,y∈T为“有时直接1因果”关系(x⇀y)⟺x→y∧(xy);
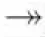
(4)变迁x1,x2,…,xk,y∈T为“有时直接k因果”关系(x1x2…xk⇀y)⟺x1x2…xk→y∧xk⇀y。
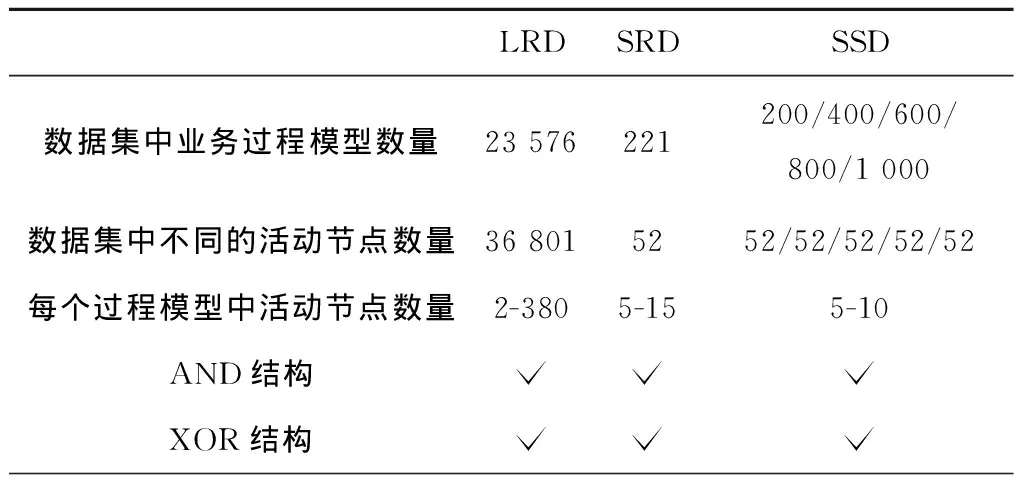
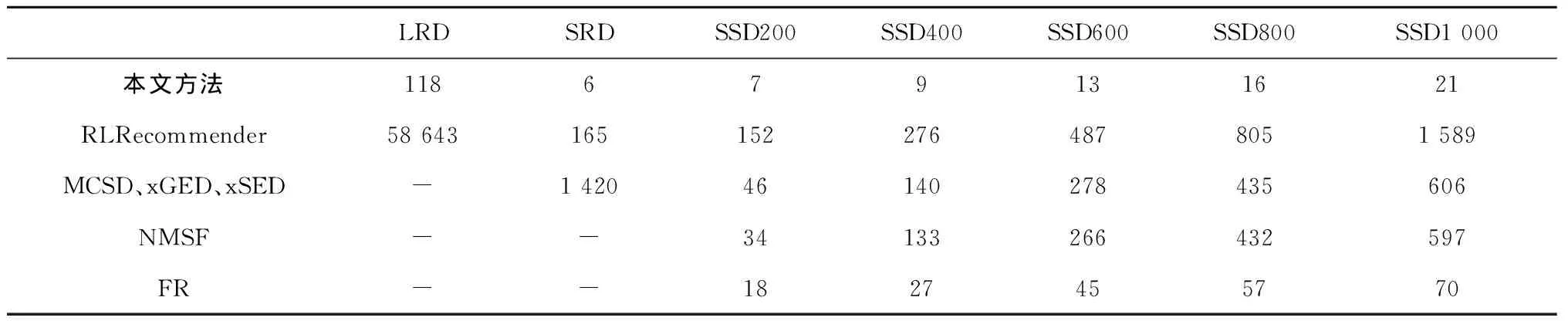
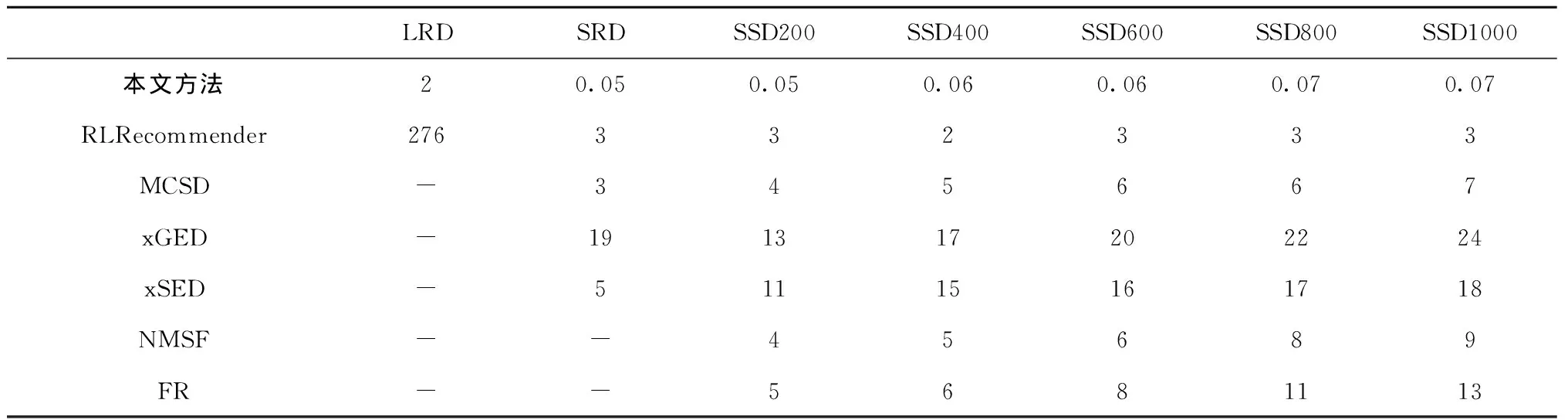
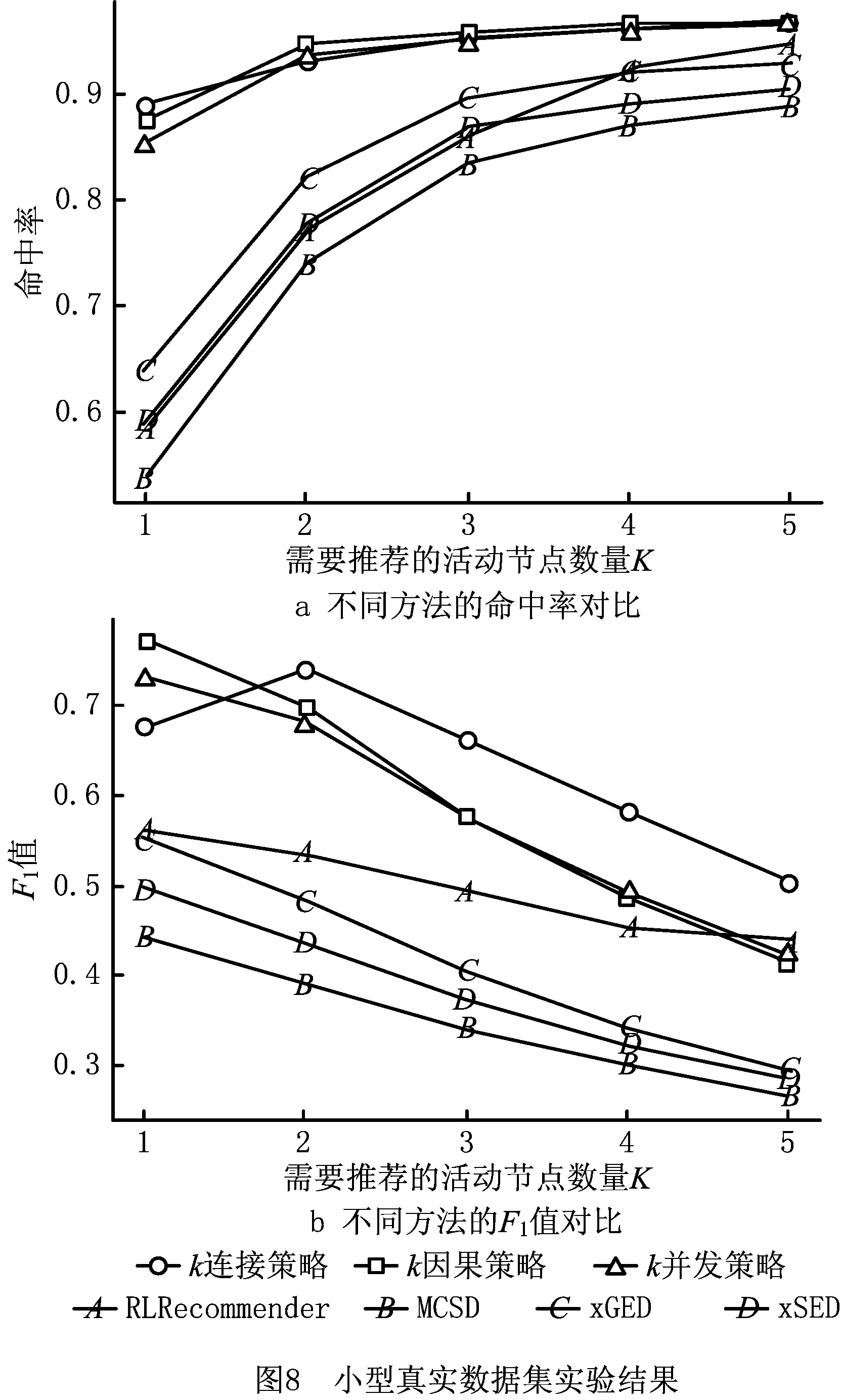
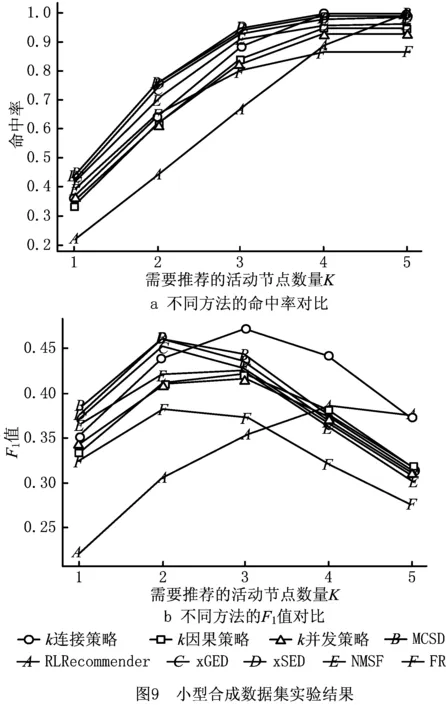
在提取“直接k因果”关系和“反向直接k因果”关系时,需要遍历每个节点的所有输出边来获得“直接1因果”关系和“反向直接1因果”关系,并将所有“直接k连接”关系最后一个连接替换为“直接1因果”关系和“反向直接1因果”关系。令n、e和x分别表示一个过程模型的节点数、边数和单个节点输出边数的最大值。从一个过程模型中提取“直接k因果”关系和“反向直接k因果”关系的时间复杂度为O(e+nxk) 定义8从不/有时/总是直接k并发。在一个合理工作流网N=(P,T,F)中: (1)变迁x,y∈T为“从不直接1并发”关系(xy)⟺∃p∈P,使得x,y∈p·; (2)变迁x,y∈T为“有时直接1并发”关系(xy)⟺∃p1,p2∈t·,t∈T,p1≠p2,使得(|p1·|>1∨|p2·|>1)∧x∈p1·∧y∈p2·∧(xy); (3)变迁x,y∈T为“总是直接1并发”关系(x‖y)⟺∃p1,p2∈t·,t∈T,p1≠p2,使得p1·={x}∧p2·={y}∧(xy)∧(xy); (4)变迁x1,x2,…,xk,y∈T为“从不直接k并发”关系(x1x2…xky)⟺x1x2…xk→y∧xky; (5)变迁x1,x2,…,xk,y∈T为“有时直接k并发”关系(x1x2…xky)⟺x1x2…xk→y∧xky; (6)变迁x1,x2,…,xk,y∈T为“总是直接k并发”关系(x1x2…xk‖y)⟺x1x2…xk→y∧xk‖y。 “直接k并发”关系可以很好地处理在同一前驱活动序列后的活动节点之间的关系。例如图1中的过程模型中,在不同k值下可以得到B‖S、CD、AB‖S和BCD。图1中的过程模型的“直接k因果”关系、“反向直接k因果”关系和“直接k并发”关系的组合(k=1或2)如表3和表4所示,表中S表示不可见任务Slient_{A,C}_{C,D}。 表3 图1中过程模型的两种“直接1因果”关系和“直接1并发”关系的组合 表4 图1中过程模型的两种“直接2因果”关系和“直接2并发”关系的组合 在提取“直接k并发”关系时,需要遍历每个节点之后所连接的活动节点对,以获得所有的“直接1并发”关系,并将“直接k连接”关系与“直接1并发”关系组合得到活动“直接k并发”关系。令n和x分别表示一个过程模型的节点数和单个节点输出边数的最大值。从一个过程模型中提取“直接k并发”关系的时间复杂度为O(nx2+nxk)。当k>2时,提取“直接k并发”关系的时间复杂度为O(nxk);当k=1时,提取“直接k并发”关系的时间复杂度为O(nx2)。 这一阶段使用生成的关系集合来进行推荐。用户首先选择策略并指定“直接k”关系中k的最大值和每种k值的权重列表,其中k表示前驱活动序列的长度。此外,未完成的过程模型中当前建模步骤后可能出现的关系可以由用户指定或由推荐方法通过已建模部分的结构得到。之后,推荐方法通过在所生成的关系集合中找到所有可能出现在当前建模步骤中的活动节点来计算每个候选活动节点的出现值,并向用户推荐具有最大出现值的前K个活动节点,其中K也是由用户指定的参数。 具体而言,算法1显示了推荐活动节点的算法伪代码。其中:在第1行~第2行中,算法通过遍历所有关系并检查关系的正确性来找到适当关系的集合。第3行~第9行计算了所有候选活动节点的出现值。对于每个k值,算法遍历了所有适当的关系和前建模步骤中的所有前驱活动序列。算法在k值对应的关系集合中找到具有当前遍历到的前驱活动序列和关系的所有三元组(前驱活动序列,关系,后继活动节点),并将该三元组在关系集合中出现的次数乘上k值对应权重添加到对应候选后继活动节点的出现值中。第10行根据每个候选活动节点的出现值对候选活动节点列表CT进行排序,且第11行将具有最高出现值的前K个活动节点推荐给用户。 算法1推荐活动节点。 输入:未完成工作流网N=(P,T,F);需要推荐的活动节点数量K;权重数组W;关系集合RS;当前建模的活动节点et∈T;et后的关系er(可选)。 输出:候选活动节点列表。 1 if er=NULL then R←{valid relations after et} 2 else R←{er} 3 CT←∅ 4 for k=1 to W.size do 5 for r∈R do 6 for Upstreamsut end with et with k transitions 7 for cts.t.(ut, r, ct.transition)∈RS do 8 if ct∈CT then ct.value←ct.value+count(ut,r,ct.transition)×Wk 9 else ct.value←count(ut,r,ct.transition)×Wk,CT←CT∪{ct} 10 sort CT by value 11 CT←{TopKitemsinCT} 12 return CT 在进行推荐时需要将k种关系集合计入出现值,并遍历r种关系。因为前驱活动序列的最后一个节点在每个建模步骤中是固定的,所以遍历所有前驱活动序列的时间复杂度是O(xk-1),其中x表示单个节点输出边数的最大值。在生成的关系集合中查找三元组的时候可以用O(1)的时间复杂度通过哈希表来完成。另外,还需要更改n个活动节点的出现值。排序部分的时间复杂度是O(nlog(n))。因此,一次推荐的时间复杂度为O(krxk-1n+nlog(n))。由于关系集合数k和关系数r为一个非常小的常数,时间复杂度约为O(nxk-1+nlog(n))。特别地,当k=1时,时间复杂度为O(n+nlog(n))=O(nlog(n))。 本文使用的数据集为大型真实数据集(LRD)[11]、小型真实数据集(SRD)[5]和小型合成数据集(SSD)[1]。表5给出了3个数据集的统计信息。 表5 实验使用的3种数据集统计信息 续表5 大型真实数据集来源于业务过程管理学术倡议(BPM Academic Initiative)[11],其中包含由学生、讲师和行业合作伙伴所创建的过程模型。在实验评估中,只使用了BPMN 1.1,BPMN 2.0和Petri网形式的过程模型。所有过程模型中的活动标签被转化为小写字母,并去除了活动标签中所有的非英文字母字符。此外,数据集中所有的非英语过程模型和只包含不可见任务的过程模型均在实验评估前被删除。BPMN 1.1和BPMN 2.0形式的过程模型都预先使用文献[12]中提出的方法转换为Petri网形式的过程模型。另外,不是合理工作流网的Petri网也会从数据集中被删除。 小型真实数据集首次用于文献[5]中,该数据集是从中国浙江省杭州市某区政府收集的各种业务过程模型。 小型合成数据集中包含了5个子数据集,这些数据集均由文献[1]中所提出的方法生成得到。 本文使用命中率和F1值作为所有推荐方法性能的评价指标。在对未完成的过程模型进行推荐时,推荐的K个活动节点列表所对应的集合由Ar表示,当前建模步骤之后应该被推荐给用户的正确活动节点集合由At表示,#hit表示推荐的活动列表中有命中的次数,#rec表示总的推荐次数。命中率表示推荐方法一次推荐中包含正确活动节点的次数占总推荐次数的百分比,其定义为#hit/#rec;准确率(precision)定义为Σ|Ar∩At|/Σ|Ar|,召回率(recall)定义为Σ|Ar∩At|/Σ|At|,F1值是准确率和召回率的调和平均值,其定义为2/(1/recall+1/precision)。 对于本文的参数设置,每个k值对应的权重为10k,这是由实验确定的。本文将k的最大值按照不同的数据集和关系提取策略设为表6中的值。所有对比方法的参数设置遵循它们在原文中的设置(因为数据集、评价指标和实验步骤均相同)。 表6 k的最大值选取 实验过程中,本文所使用的服务器包含两个Intel Xeon E5-2620 v4@2.10 GHz CPU、128 G RAM和3个GeForce GTX 1080Ti GPU。 本文在两个小数据集上进行实验评估时使用五重交叉验证法。另外,小型合成数据集在5个子数据集上所有评价指标的平均值被用来作为该方法在整个小型合成数据集上的实验评估结果。对于大型真实数据集,本文将数据集中的23 576个业务过程模型分为测试集(3 041个模型)、验证集(1 759个模型,用于寻找最佳参数)和训练集(18 776个模型),并确保在测试集中出现的所有活动节点都会出现在训练集中。对于每个业务过程模型,实验将重复对每一个位置进行推荐,直到整个业务过程模型完成建模。 在进行效率对比时,本文对所有推荐方法两部分的时间进行了计算:①数据集处理部分,这部分计算了从输入数据集开始到处理信息完成的时间,这部分只会被执行一次,且结果信息将被保存在后端供推荐使用;②推荐活动节点部分,这部分计算了每个建模步骤中推荐的时间。表7和表8所示为所有数据集上所有推荐方法运行所需要的时间。可以发现,本文提出的方法在数据集处理部分以及推荐活动节点部分均快于其他方法。 表7 推荐方法数据集处理的时间对比 s 表8 推荐方法每次推荐活动节点的时间对比 ms 由于现有其他推荐方法无法处理大型真实数据集,本文方法在该数据集上仅和RLRecommender[6]进行比较。图7显示了LRD上需要推荐的活动节点数量K为1~10的实验结果。 由图7可以发现,本文方法中的3种策略在两个评价指标上均优于RLRecommender中的3种策略。当K=10时,本文方法的命中率达到了92.12%。另外,RLRecommender无法处理K很小的情况,特别是当K=1时,RLRecommender的两个指标都低于10%。相反的,本文方法在K很小的时候表现依然良好。 因为文献[1]和文献[3]中的推荐方法无法处理该数据集中的循环结构,所以在该数据集上本文方法只和RLRecommender[6]以及文献[5]中的MCSD、xGED和xSED进行了比较。实验结果如图8所示。 由图8可以发现,当K为1~5时,本文方法中的3个策略在两个评价指标上的表现全面优于其他方法,这表明本文方法完全可以应用于现实数据集。当K=1时,本文方法命中率和F1值上的最高值相比其他推荐方法的最高值分别提升了25.1%和21.1%;当K=5时,本文方法命中率和F1值上的最高值相比其他推荐方法的最高值分别提升了2.1%和6.5%。 在小型合成数据集上,本文方法与RLRecommender[6]、FlowRecommender(FR)[1]、NMSF[3],以及文献[5]中的3种方法MCSD、xGED和xSED进行了比较。小型合成数据集中含有200~1 000个过程模型的5个子数据集结果的平均值如图9所示。 由图9可知,当K=5时,本文方法的命中率与其他推荐方法的最高值相同,达到了99.99%。随着K增加,本文方法在F1值上也优于其他基于子图结构的推荐方法(MCSD、xGED、xSED、NMSF和FR)。当K=5时,本文方法在F1值上的最高值相比其他基于子图结构的推荐方法的最高值提升了5.6%。当K很小时,本文方法与其他基于子图结构的推荐方法相比并没有优势。这是因为小型合成数据集中的子数据集很小,且不包含任何复杂结构。 本文提出了基于前驱活动序列和后继活动节点之间结构关系的推荐方法。首先,该方法对所有不可见任务进行打标。随后,在指定前驱活动序列的长度之后,从前驱活动序列和后继活动节点之间用3种策略提取出3种关系集合。最后,在指定不同前驱活动序列长度所对应的权重之后,该方法通过计算每个活动节点的出现值来推荐适当的活动节点。实验表明,该方法在所有数据集上的运行效率和正确性均优于现有其他推荐方法。 未来将研究如何使该方法能够推荐不在过程模型数据集中的结构。这可以使用过程模型活动节点间的非直接的关系,因为有一些活动节点可能并没有直接连接但也会一起出现。另外,在预处理时,可以对活动节点标签进行初步聚类,因为一些文本不同的活动标签可能代表完全相同的活动节点。
4.3 推荐活动节点
5 实验评估

5.1 推荐方法效率对比
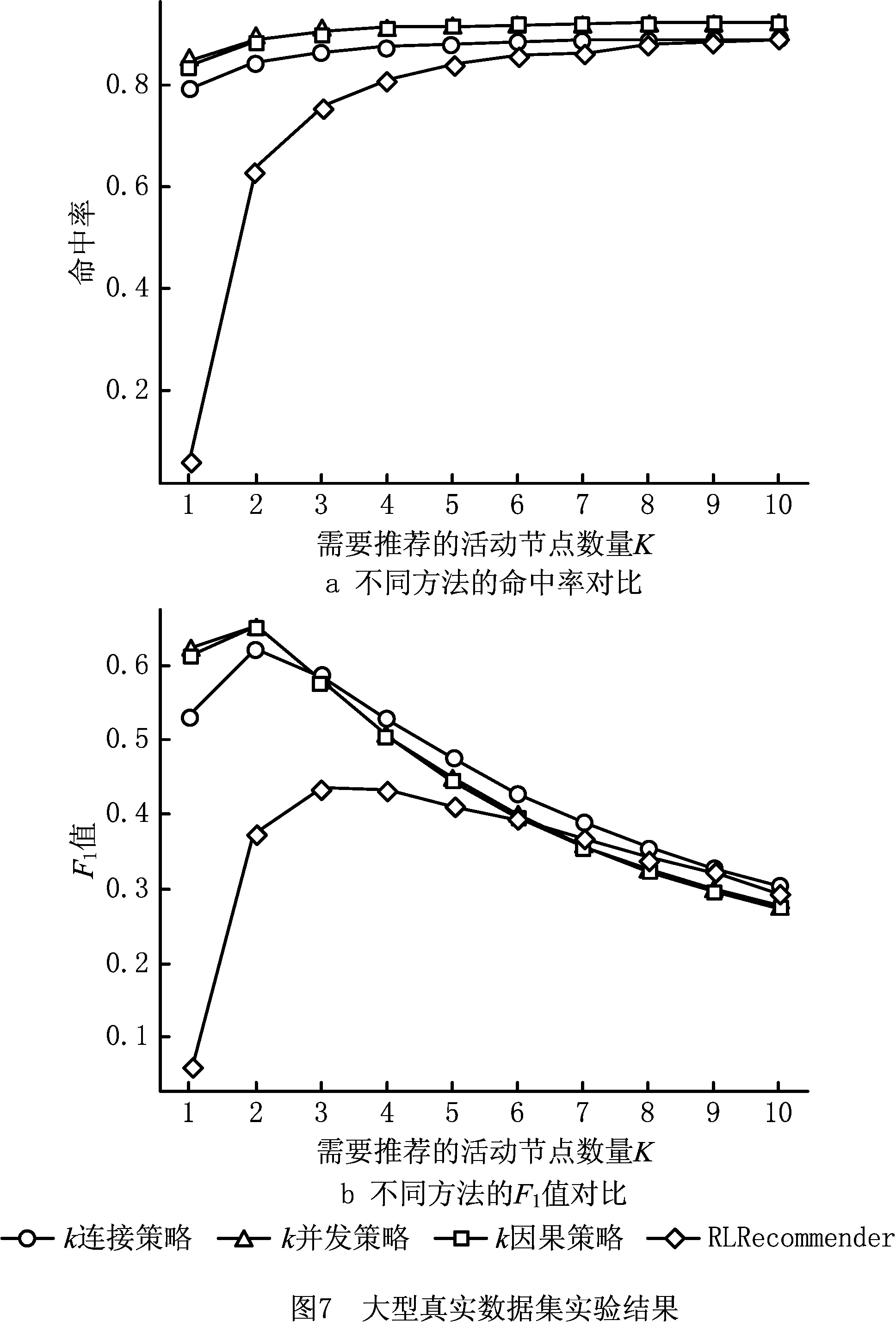
5.2 大型真实数据集上的实验评估
5.3 小型真实数据集(SRD)上的实验评估
5.4 小型合成数据集上的实验评估
6 结束语

