基于信息熵的无标日志划分评价方法
林雷蕾,杨 良,闻立杰+,周 华,王建民
(1.清华大学 软件学院,北京 100084;2.浪潮通用软件有限公司,山东 济南 250101;3.西南林业大学 大数据与智能工程学院,云南 昆明 650224)
1 问题的提出
过程发现(process discovery)是过程挖掘(process mining)领域的核心应用场景,该场景旨在从日志数据中挖掘出准确的业务过程模型,进而指导或优化企业的业务管理。为了从日志中得到过程模型,van der Aalst等提出了经典的Alpha算法[1],该算法能从日志数据中挖掘出合理的Petri网模型。此后,众多国内外学者在此基础上提出了扩展的Alpha系列算法,如:Guo等[2]提出了α$算法,用于解决不可见任务和非自由选择结构的挖掘难题;Lekic等[3]提出α||算法旨在从完备性更弱的日志中挖掘出活动之间的顺序和并发关系;林雷蕾等[4]提出了αL+算法用于解决二度循环挖掘难题。此外,还有一些优秀的模型发现算法如:Inductive Miner算法[5]、启发式挖掘算法[6]和遗传挖掘算法[7]。
然而,现有算法在挖掘实际企业产生的日志数据时,容易得到一个相当复杂和难以理解的过程模型,造成该问题的主要原因有:①日志数据中执行活动的颗粒度不一样;②实际过程模型不一定是结构化的,活动之间的关系较为复杂;③日志数据中混合存在多个模型产生的数据。针对第①个问题,可以通过映射聚类的方式将低层次的多个小颗粒度的事件(event)映射到高层次的活动(activities)中[8];针对第②个问题,主流的方式通过轨迹聚类(trace clustering)方式将日志聚成不同子日志,然后再逐一对子日志进行挖掘[9-10];针对第③个问题,现有概念漂移(concept drift)检测算法的目的就是找出日志数据中的变化点,从而将日志划分为不同子日志,进而挖掘出过程模型的不同演化版本[11-13]。本文立足点是概念漂移中无标日志的划分评价问题,如图1所示为日志划分与轨迹聚类的异同点:从数据处理结果来看,二者目标都是将原始日志分为多个子日志(sub-log)。但是,如图1b所示,大部分轨迹聚类只考虑轨迹之间的相似度,不考虑轨迹出现的位置(即轨迹的时间属性),然而日志划分是根据时间点来将前后日志切割成不同的子日志。

现有日志划分的评价方法都是基于有标的F-score来评价[11-14],即事先知道变化时间点的位置和数量。然而,现实情况是大部分日志数据都是无标的,即不知道变化时间点的位置和数量。为此,本文基于信息熵提出一种新的评价方法,其主要创新点在于:①解决了无标日志划分的评价问题;②提出了内部熵及外部熵的定义,用于衡量日志划分的内聚度和耦合度;③引入惩罚因子来调节算法偏好。
2 相关工作
将日志分为多个子日志的评价方式大致可分为基于有标的评价方式、基于模型发现的间接评价方式、基于高内聚低耦合的直接评价方式3类。
(1)基于有标的评价方式,其核心思想是事先对日志数据进行标注,然后以此衡量哪种划分结果更接近实际标注的基准。文献[11-14]都是基于F-score的方式来评价日志划分的质量,该方式事先知道了变化点的数量和位置,然后利用准确率(precision)和召回率(recall)来衡量某种划分方法的最终得分,但这种做法无法适用于实际的企业数据。这是因为实际生产过程中很难获取到有标注的日志数据,而依靠人为标注的方式又会浪费大量人力物力。
(2)基于模型发现的间接评价方式,其核心思想是利用挖掘算法分别得到不同子模型,然后再计算出每个子模型与子日志之间的评价指标,最后综合得出日志划分的质量。常用评价指标包括拟合度(fitness)、准确度(precision)和复杂度(complexity)等[15-17]。间接评价方式虽然克服了无标难题,但评价过程严重依赖于过程挖掘算法。换句话说,同一个划分,采用不同挖掘算法得到的评价指标可能不同。为此,如何选择合适的挖掘算法是这类评价方式的难题。
(3)基于高内聚低耦合的直接评价方式,其核心思想是利用同一个模型的多条轨迹具有高内聚原则来评价日志的划分。文献[10]提出了簇间集合熵(cluster set entropy)概念,用于评价轨迹聚类的质量,但是该评价方法没有考虑轨迹之间的时间属性。在日志划分研究方面尚未见到直接评价的方法。
综上所述,基于有标的评价方式和基于模型发现的评价方式都存在不足,而针对无标日志数据的划分评价仍然是空白。为此,本文借鉴集合熵的思想,提出划分熵(partition entropy),用以评价日志划分的质量。
3 预备知识
首先对论文中涉及的基本概念进行阐述。
定义1事件日志与轨迹[18]。假设T为所有任务集合,σT*是一条事件轨迹,W(T*)是一个事件日志。
由定义1可知日志是轨迹的集合(幂集表示),而每条轨迹又是由有限个任务按照执行次序排列而成。
定义2直接后继关系()[18]。假设T是任务集合,W(T*)代表事件日志。对于a,bT,ab,当且仅当:存在一条轨迹σ=t1t2t3…tn-1tn,而i{1,…,n-1},其中σW且ti=a,ti+1=b。
定义3局部完备性[18]。T代表有限的任务集合,令W(T*)代表事件日志,则W满足局部完备性的条件是:①假设σ是模型N产生的任意一条执行轨迹,则满足σ⊂W;②对于t∈T,必存在一条轨迹σ∈W且t∈σ。
4 日志划分的评价方法
本章将讨论如何对日志划分进行评价,主要包括3个核心步骤(如图2):①首先定义了日志数据中的轨迹变体,作为衡量数据的随机变量;②根据随机变量来计算每个划分内部的信息熵以及相邻划分之间的分布距离(称为外部熵);③利用惩罚因子对极端算法进行惩罚,使得最终划分尽可能合理。

4.1 轨迹变体
由定义1可知,日志是轨迹的集合,一条轨迹代表一次完整的业务执行过程。为此,无论是轨迹聚类还是日志划分,都是以轨迹作为基本的计算单元。受此启发,本文在计算日志划分的分布时,定义了轨迹变体作为随机变量。首先给出轨迹关系等价及轨迹变体的定义。
定义4轨迹关系等价(≡)。假设T是任务集合,W(T*)代表事件日志。对于任意两条轨迹σ1,σ2∈W,若两条轨迹关系是等价的,σ1≡σ2,则当且仅当:两条轨迹直接后继关系的集合相等,表示为σ1=σ2。
定义5轨迹变体tv。假设T是任务集合,W(T*)代表事件日志。对于任意两条轨迹∀σ1,σ2∈W,若σ1和σ2不满足σ1≡σ2,则称轨迹σ1和σ2分别属于两个不同的轨迹变体,记为tv1和tv2;若σ1和σ2满足σ1≡σ2,则称轨迹σ1和σ2分别属于同一个轨迹变体,记为tv1。
定义4表明,轨迹关系等价即轨迹的所有直接后继关系都是相等的。换句话说,轨迹σ1中所有直接后继关系都会在轨迹σ2中出现,反之亦然。在等价(≡)的基础上,给出了轨迹变体的定义5。直观讲,两条轨迹如果是等价的,则同属于一种轨迹变体。例如,假设σ1=〈a,b,e,b,c,d〉,σ2=〈a,b,e,b,e,b,c,d〉,两条轨迹是属于同一种轨迹变体的,因为两条轨迹的直接后继关系都是{ab,be,eb,bc,cd}。另外,之所以不用轨迹中活动集合作为日志数据的变量,是因为活动集合一样的轨迹,后继关系也不一定等价。需要说明的是,轨迹变体是基于直接后继关系定义的,作为后续划分熵的随机变量。但用户可根据实际情况自定义刻画日志随机变量的单位,如:可以考虑间接依赖关系作为轨迹变体定义的基础,不影响后续的评价方法。换言之,刻画日志数据的随机变量是可扩展的。
4.2 内部熵和外部熵
4.2.1 内部熵
日志划分首先满足的第一个准则就是每个划分里面的轨迹全部来自于同一模型。但是,由于过程模型未知,因此根据当前划分,应该是尽可能将同属于一个轨迹变体的轨迹划分在一起。如图3所示,过程模型1是包含一个选择结构的流程,而随着业务的缩减(如经费缩减等)演变为了过程模型2。模型1不管产生多少条轨迹,只能包含两种类型的轨迹,即σ1=〈a,b,d〉和σ2=〈a,c,d〉。在例子中,分别称之为变体tv1和变体tv2。同理,模型2只能产生变体tv1的轨迹。假设一个事件日志W,前面90条轨迹中包含了tv1变体的轨迹有30条,tv2变体的轨迹有60条,且第89条轨迹为属于tv2变体的轨迹。现假设从第90条开始到199条轨迹,都是属于变体tv1的轨迹。如果一个划分点是90,另外一个划分点是100,在无标的情况下,直观判定是90这个划分点更好,因为这个划分使得前后的子日志内聚度更高。
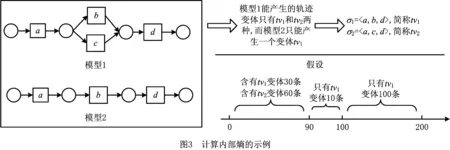
受文献[10]集合熵的启发,本文提出了内部熵IE,用于衡量日志划分后整体内部信息的混乱程度。
定义6内部熵(IE)。假设T是任务集合,W(T*)代表事件日志。对于W的一个划分[sub-log1,sub-log2,…,sub-logk],其内部熵
(1)
式中:n为日志W的所有轨迹数量,ni表示第i个子日志的轨迹数量,v表示第i个子日志中所有轨迹变体的种类数量,mj表示第j种轨迹变体在子日志i中的数量。

(2)
(3)
通过式(2)和式(3)的计算可以得出,根据这90个变化点来划分,使得整体内部熵的值更低,即混乱程度更低,从而表现出的划分结果更好。该结果与直观的分析结果一致,从而体现了内部熵IE具有一定的可靠性。
4.2.2 外部熵EE
日志划分评价的第二个准则是不同划分之间的轨迹分布差距尽可能大。为了衡量两个概率分布之间的差异,引入相对熵(relative entropy),亦称KL散度(Kullback-Leibler divergence)[19]。相对熵用于衡量两个随机分布之间的距离时,若分布相同,则相对熵为零;若两个随机分布差异较大,则相对熵的值也会增大。下面首先给出相对熵的定义。
假设相同事件的空间里,两个概率分布分别是P和Q,其中随机分布P中第i个事件变量的概率用p(xi)表示,随机分布Q中的第i个事件概率用q(xi)表示,则P与Q的相对熵
(4)
在相对熵的基础上,本文给出了用于衡量两个子日志之间差异程度的外部熵(EE)定义。
定义7外部熵(EE)。假设T是任务集合,W(T*)代表事件日志。对于W的一个划分[sub-log1,sub-log2,…,sub-logk],其外部熵
(5)
式中:n为日志L的所有轨迹数量,ni表示第i个子日志的轨迹数量,v表示第i个子日志中所有轨迹变体的种类数量,pji表示第j种轨迹变体在第i个子日志中的概率(即轨迹变体出现的数量除以子日志中所有轨迹的数量),qjr表示第j种轨迹变体在相邻子日志r中的概率,m是与第i个子日志相邻的其他子日志数量。
由式(5)可以看出,其核心本质就是利用相对熵计算两个子日志之间的轨迹变体分布差异。在计算过程中,并不是所有子日志两两之间都会计算分布差异,而是只计算相邻的子日志,其原因如图4所示。假设变化点为Ti和Tj,则原来日志被划分为3个子日志:第一个子日志sub-log1包含T0至Ti内的轨迹;第二个子日志sub-log2包含Ti至Tj内的轨迹;第三个子日志sub-log3包含Tj至Tn内的轨迹。针对当前漂移点Ti的不同位置划分,sub-log1里面的轨迹变体可能属于本身,也可能是属于子日志sub-log2(表示为图4中从sub-log1指向sub-log2的打钩曲线)。但是,绝不可能是不属于前两者,跳到属于子日志sub-log3(表示为图4中从sub-log1指向sub-log2的打叉曲线)。因为,日志划分时考虑了轨迹的时间属性。即相邻时间段的轨迹才有可能来源于同一个模型。同理,由于子日志sub-log2存在两个相邻的子日志(sub-log1和sub-log3),根据漂移点划分的不同,子日志sub-log2里面的轨迹可能被划分到3个子日志中的任何一个子日志。
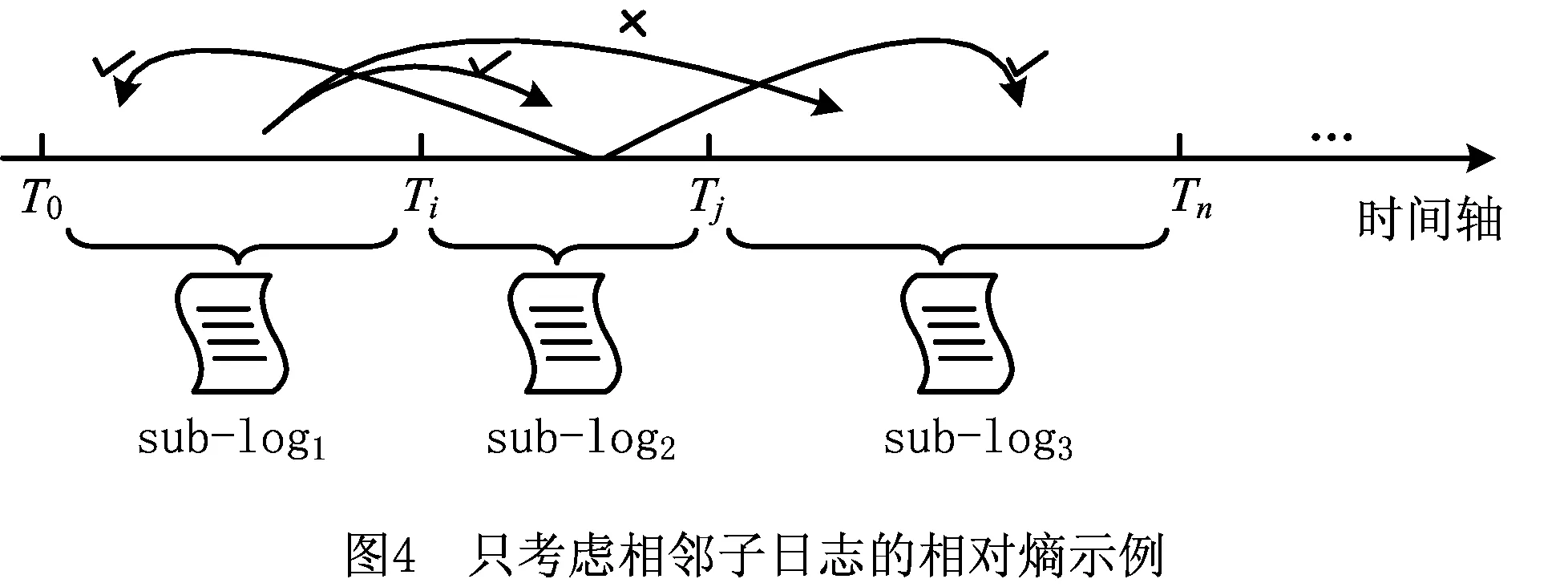
另外,在计算外部熵EE时候,需要统计两个变量的概率p(x)和q(x),分别代表轨迹变体x在当前子日志中的概率和相邻子日志中的概率。一般来说,若p=0,则plog2(p)=0。若p≠0,且q=0,则D(P||Q)接近无穷大。换言之,若相邻划分的子日志中,存在互相都没有的轨迹变体,则外部熵的计算就会失效,这也是KL散度的缺陷。为此,本文提出平滑映射,将所有变量映射到统一的变量空间中。
定义8平滑映射()。假设事件日志L根据漂移点划分的子日志为[sub-log1,sub-log2,…,sub-logk],令P和Q分别为子日志sub-logi和sub-logj的轨迹变体分布,i,j∈{1,2,…,k}且i≠j,若分布P中存在n个随机变量且有TVr={tvh+1,tvh+2,…,tvh+r}∉TVm,h+r≤n,其中TVm为Q的随机变量集合,TVm={tv1,tv2,…,tvm},且则对于给定概率常数(∈(0,1)),Q′为Q的一个平滑映射,表示为QQ′,当且仅当:①Q′的变体集合TV=TVr∪TVm;②Q′中的轨迹变体概率为∀tv∈TVr,q(tv)=,且∀tv其中q(tv′)为tv在原来Q分布中的概率。
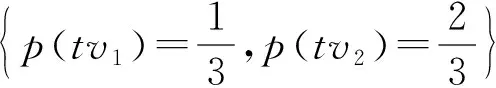
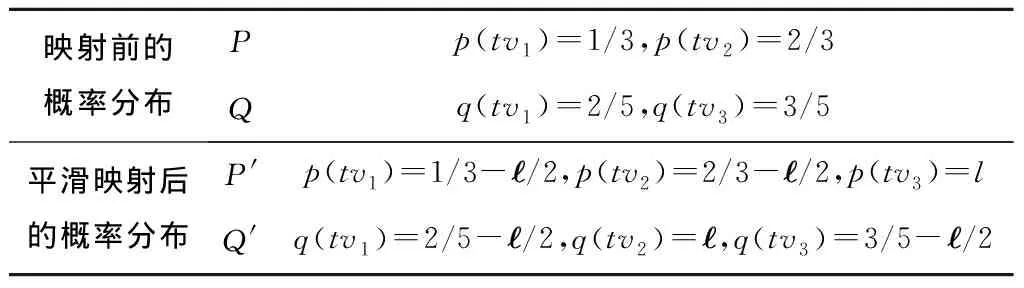
表1 针对图4假设的轨迹分布P和Q进行平滑映射的结果
最后需要注意的是,由于相对熵在衡量两个概率分布之间的差异时是一个非对称性的度量值,因此采用两个子日志之间的平均值来作为两个分布之间的距离。即令D(P′,Q′)为两个分布之间的距离
(6)
式中:EE(P′||Q′)表示子日志sub-log1到子日志sub-log2的距离,EE(Q′||P′)表示子日志sub-log2到子日志sub-log1的距离。
4.3 惩罚因子
内部熵IE衡量的是子日志内部的内聚度尽可能高,外部熵EE衡量的是子日志之间的差异尽可能大。然而,由于过程模型都存在选择或者并发结构,某些划分算法为了迎合评价指标,就会出现暴力的划分方法,即每个轨迹变体划分为一个子日志。
如图5所示,假设原有模型为M1,其产生的日志为σ1到σ4。现有一个划分算法,将前面两条轨迹划分为一个sub-log1=[σ1,σ2],后面两条轨迹划分为另外一个sub-log2=[σ3,σ4]。由于每个子日志都只含有一种轨迹变体,因此该划分的内部熵IE和外部熵EE得分都比较好。但是,通过对子日志挖掘发现每个划分得到的过程模型都是一个顺序结构,即为原有模型的一次执行过程。如图5中子日志sub-log1挖掘得到的模型是M1,子日志sub-log2挖掘得到的模型是M2。因此,这种划分结果会导致模型失去泛化能力,偏离了过程挖掘的本质。为避免此类问题的发生,本文提出了惩罚因子Bias。

定义9惩罚因子Bias。假设[sub-log1,sub-log2,…,sub-logk]为事件日志W的一个划分,|sub-logi|代表子日志i中的轨迹数量,i{1,2,…,k},对于给定的轨迹数量λ,λ为正整数,∀sub-logi{sub-log1,sub-log2,…,sub-logk},若|sub-logi|<λ,则对该子日志的划分信任度较低,令h为信任度较低的子日志数量,k≥h≥0,整个划分的偏好
(7)
Bias的本质就是对划分子日志中轨迹数量小于给定观察数量λ的子日志进行惩罚。由于每个局部子日志的不确定划分都会对整体划分造成影响,对每个子日志的惩罚增量都是1/k,累加后就变为h/k,其中k为所有子日志数量,h为小于λ的子日志数量。换言之,若子日志中轨迹数量越多,则认为模型的关系越完备,因此子日志的划分可信度较高。参数λ为用户设定值,本文默认λ=200。
4.4 划分熵
在内部熵IE、外部熵EE及惩罚因子Bias的基础上,最终得到划分熵
(8)
划分熵的初衷是通过合理的划分,使得日志整体的混乱程度达到最低。对比式(8),内部熵IE刻画的是内聚度,因此IE的值越小,PE的值也越低(EE和Bias不变的情况下)。同理,作为分母的外部熵EE值越大,PE的值越小。对于惩罚因子Bias,最好的期望就是取值为0的时候,PE趋向于高内聚低耦合。同时,当EE<1时,将使得PE的值偏大,这与初衷不吻合。换言之,只要存在距离,EE应该就是对PE有益的。为此,引入一个平衡系数β=1。此外,平衡系数还有一个作用就是当EE=0的时候,使得划分熵PE只与内部熵IE和惩罚因子Bias有关,这是合理的。需要说明的是,内部熵IE和外部熵EE默认不会出现取值为0的情况。
算法1给出了划分熵PE的计算过程:伪代码第1~第3行是计算子日志中的轨迹变体过程。其中,为了保证不同子日志中相同轨迹变体的变量名一致,首先扫描一遍所有子日志,统计出轨迹变体的种类(第2行)。然后,再分别计算出每个子日志中的轨迹变体分布(第3行)。第4行是利用轨迹变体直接计算出每个子日志的内部熵IE。第5行是通过遍历来计算相邻子日志间的距离,而且每次计算之前都要对两个日志进行平滑映射(第5.1行)。第6行是根据用户设定的参数λ来惩罚划分是否合理。最后,利用式(8)将内部熵IE、外部熵EE以及惩罚因子Bias整合起来,计算出整个日志划分的划分熵PE。
算法1划分熵partitionEntropy()。
输入:日志L,划分点集合Drifts,超低概率常数,最小轨迹数量λ;
输出:划分熵PE。
BEGIN
1. ListSub-log←split L based on Drifts;//根据划分点得到不同子日志
2. ListTV←extracting trace variants from L;//统计所有变体种类
3. ListSub-log TV←computing based on ListTV and ListSub-log;//求子日志的变体
4.IE←Equation(3-1);
5.WHILE i 5.2.EE←Equation(3-5); 6.Bias←根据λ计算Equation(3-7); 7.PE←Equation(3-8); 8.RETURN PE; END 为了评估划分熵PE的有效性,本章利用已公开发表的数据集进行测试。此外,与有标的F-score评价方法对比,表明方法的可靠性。最后,对本文方法进行了进一步讨论。 如图6[12]所示为一个实际的贷款申请业务模型。模型中有19个活动,且同时存在循环、并发和选择结构。此外,文献[12]定义了18种修改模式,分别是:CB,CD,CF,CM,CP,FR,LP,PM,RE,RP,SW,PL,OIR,ORI,IOR,IRO,RIO,ROI,用于对图6中的基准模型进行不同修改,从而得到相应的修改模型。然后,再通过两种模型仿真出不同量级的数据进行混合,得到最终的测试日志数据。目前,公开的日志数据有4种量级,分别是包含2 500条轨迹的2.5 k日志、包含5 000条轨迹的5 k日志、包含7 500条轨迹的7.5 k日志以及包含10 000条轨迹的10 k日志。每个量级的数据都对应18种修改模式,因此共有72个日志数据。这些日志数据是事先知道变化点的位置和个数的(每个数据有9个变化点,每个变化点都相隔10%条轨迹的距离)。 概念漂移是为了发现日志数据中的变化点,从而将日志划分为多个子日志。常见的漂移类型有突发漂移(sudden drift)、渐变漂移(gradual drift)、周期漂移(recurring drift)和增量漂移(incremental drift)[11-14]。从日志划分的角度来讲,无论是哪种漂移检测,本文方法均适用。为此,本文选取了当前引用率及准确率较高的两种算法进行对比,分别是文献[12]中的Run和文献[13]中的TPCDD(Tsinghua process concept drift detection)。在测试时,选取了18种模式中具有代表性的ROI2.5k日志进行详细的说明,然后再对10 k量级的所有18模式数据进行测试。 如表2所示,日志ROI2.5k的划分标准答案是每250条轨迹有一个划分点,最后的划分熵PE=0.459。TPCDD和Run的划分熵分别是0.473和2.400,从而表明无标评价下TPCDD的划分质量更好。直观地,从表中可以看出,确实是TPCDD方法得到的结果更接近标准划分的答案。随后,本文随机对该日志进行了不同程度的划分,如random-90代表每隔90条轨迹给一个划分点,其他的类似。另外,random方法是随机划分,没有固定间隔。而random-all方法是不对日志进行划分,即没有划分点。可以看到,无论哪种随机划分的结果,其划分熵PE都比标准答案的值要高,表明划分得不好。表2还有一个特殊之处,就是random方法、random-200方法、random-150方法和random-90方法划分的结果都比Run方法好,即PE值更低(其他17种修改模式中,这几个方法的PE值基本都是比Run方法高)。为了验证本文的划分熵PE是否可靠,针对上面划分的结果,再次用有标的F-score方法对随机方法中的3种和Run进行对比,结果如图7所示。 表2 日志ROI2.5k不同划分方法对应的划分熵PE 在图7中,横坐标是滞后区间不同的取值,滞后区间可以理解划分点为与标准答案的容忍区间,即容忍区间越小,越接近真实答案,但准确率也会下降;纵坐标是不同区间值所对应的F-score得分。可以看到,无论滞后区间取值为多少,random、random-90和random-200三种划分方法的得分都高于Run。这个结果与表2分析的结果一致,从而表明本文提出的划分熵PE是可靠的。此外,在滞后区间取值为30时,虽然random-200得分比random-90低,但是其他3个值都比random-90好。综合分析,random-200是优于random-90的,与表2的分析结果一致。 如图8所示,本文对10 k量级日志数据的18种修改模式分别计算了TPCDD和Run两种方法的划分熵PE。由图8可知,TPCDD的划分结果整体上好于Run方法,因为除了IRO和OIR两种模式的值比Run高一点以外,其他模式下的PE值平均下来都比Run的PE值低。该分析结果与文献[13]采用有标F-score分析的结果一致,从而表明了本文提出的评价方法是可行的。 日志划分的出发点通过划分得到不同子日志数据,从而提升模型的发现质量。当前,针对日志划分的评价集中在有标的评价方式上,而实际生活中很难获取有标的日志数据。为此,本文提出一种无标日志数据的划分评价方法——划分熵PE。首先,定义了轨迹变体用于表示子日志的变量分布。其次,提出内部熵和外部熵分别用于衡量划分后子日志内部的内聚度和子日志之间的距离。为避免某些算法盲目地迎合评价指标,本文利用惩罚因子对暴力划分的方法进行惩罚。最后,对多组数据进行测试,并与有标的F-score方法进行对比,表明了本文方法的可行性。下一步,将提升评测方法在噪音数据上的鲁棒性,以及针对事件流日志的评测。5 实验评估
5.1 评估案例
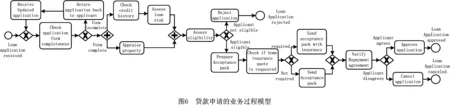
5.2 算法评估

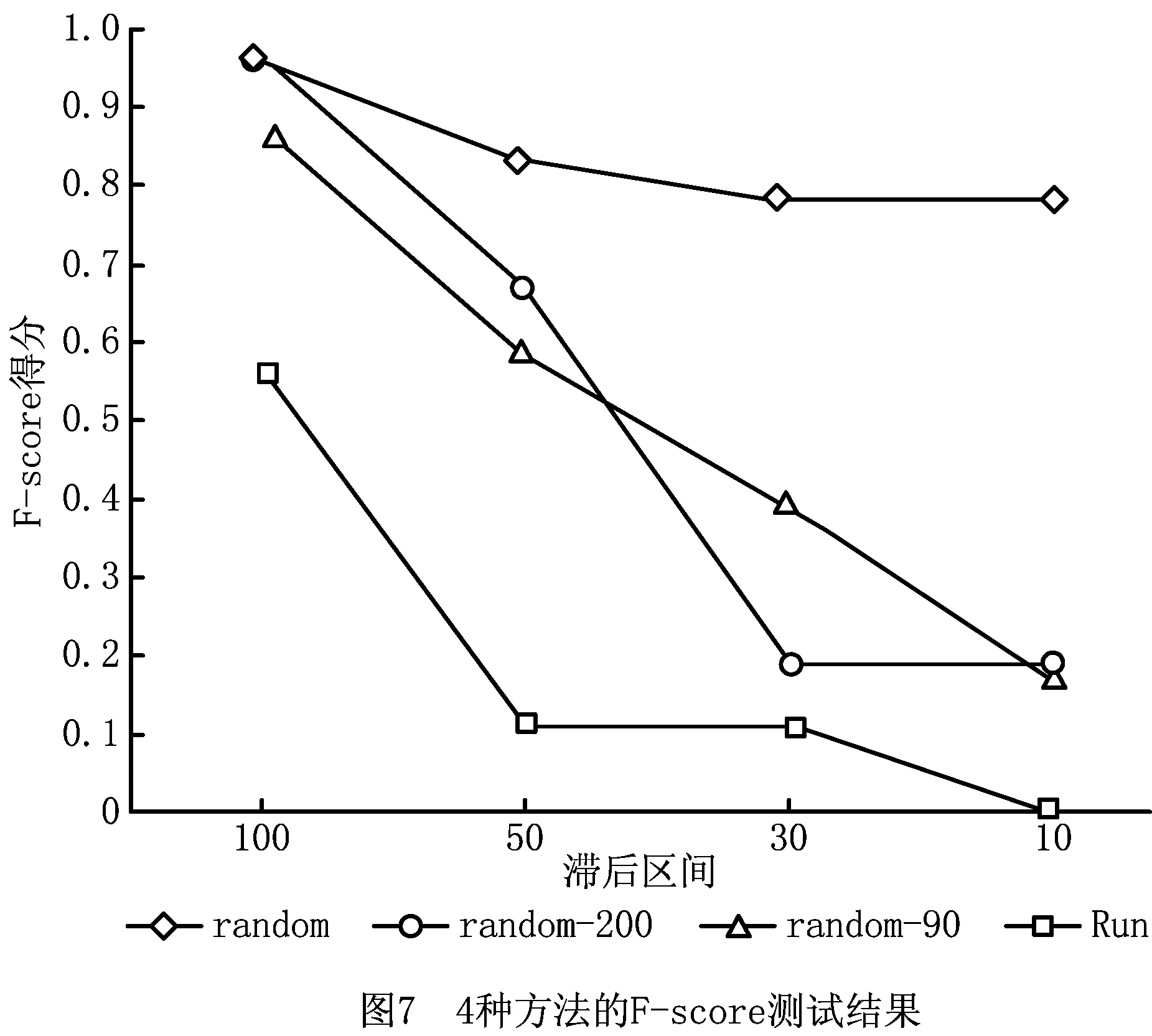
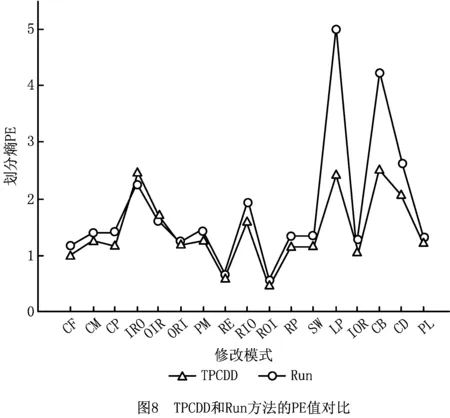
6 结束语

