基于近似似然的频响函数不确定性模型修正*

邓振鸿， 张保强， 苏国强， 郭勤涛

(1.厦门大学航空航天学院 厦门，361005) (2.南京航空航天大学机电学院 南京，210016)

引 言

在许多工程问题中，所建立的仿真模型的准确度对于结构的设计分析至关重要，模型修正作为一种提高仿真模型可信度的手段，旨在借助试验数据来校准仿真模型[1]。实际工程中，结构设备在制造加工误差、运输损伤及测试过程中的主客观因素等的影响下，使得系统中存在诸多不确定性，从而造成多次试验的结果存在一定的分散性。如何准确定位这些分散性即不确定性的来源并将不确定因素识别出来，已经成为研究人员关注的重点。

不确定性模型修正技术是在传统的确定性模型修正的基础上，结合概率或非概率等统计学手段，对仿真模型进行修正。Beck等[2]提出了贝叶斯框架下的不确定性模型修正。Collins等[3]在处理振动测量数据的随机误差时，引入线性灵敏度方法，以测量数据的协方差矩阵的逆作为权重，通过加权最小二乘法来获得未知参数的统计量。文献[4-6]基于文献[2]的框架，发展了其他模型修正方法，并应用在各种线性和非线性动力学系统中。文献[7-8]发展了随机模型修正理论，提出了梯度回归方法，并应用到一系列物理结构中。文献[9]比较了贝叶斯方法和摄动法，并将两种不确定性修正方法应用到DLR AIRMOD结构上加以对比验证。方圣恩等[10]利用随机响应面模型的快速运算特性来反演得到参数的均值和方差。陈喆等[11]研究了考虑试验模态不确定性的有限元模型修正方法。

上述不确定性模型修正研究均是以结构振动的模态参数作为输出响应量进行的，相比于模态参数，结构振动的频率响应量，如频响函数(frequency response function, 简称FRF)则包含了结构更充分的信息，能够更加准确地反应结构的动力学特性。同时，采用频响函数进行模型修正可以有效避免由模态分析所引入的误差。文献[12-15]介绍了频响函数驱动的模型修正研究，但均属于确定性修正范畴内的工作。Mares等[16]基于贝叶斯方法以三自由度质量弹簧系统频响函数的不确定性修正为例，比较了不同频率点的选择策略，发现靠近共振峰处的频率点应该被舍去，但仍没有得到很理想的修正效果。Arora等[17]针对动力学系统中存在的密集模态和阻尼问题，提出了一种基于复频响的参数不确定性修正方法。Hegde等[18]将单自由度二阶系统频响函数的幅值和相位分离，构建出参数与响应之间的线性模型，并采用极大似然估计方法反演出参数的均值和方差。Vakilzadhe等[19]在阻尼平衡模型校准技术的基础上，引入Bootstrating方法对试验频响函数重复采样，提出了一种新的随机有限元模型修正框架，可用于处理含有噪声的频响函数模型修正问题。Machado等[20]将随机场理论同基于灵敏度的频响函数模型修正方法结合起来，对梁材料随机场特性进行估计。Zhang等[21]同时考虑了参数和模型形式引起的不确定性，基于贝叶斯方法对重复测量的频响函数进行了不确定性校准研究。曹诗泽[22]对基于频响函数的结构有限元模型修正的不确定性量化方法进行了研究，基于频率响应函数的概率模型，提出了频响函数驱动的贝叶斯模型修正方法，并采用渐进马尔科夫蒙特卡洛算法进行求解待修正参数的最优解及后验概率密度函数。

传统的贝叶斯模型修正通常假设不确定性参数服从正态分布，而实际工程中由于试验数据有限，其样本的分布特性并不明显，从而影响似然函数的选择。因此，笔者在贝叶斯框架下，引入近似贝叶斯计算(approximate Bayesian computation, 简称ABC)理论[23]，采用区间作为参数的统计量，提出了一种适用于频响函数的似然函数，使用DREAM算法对不确定性参数进行识别，统计出参数的后验范围，并分别采用了三自由度数值算例和H型非对称梁的有限元模型修正算例加以验证。

1 基于频响函数的不确定性模型修正理论

对于多自由度振动系统，其动力学方程为

(1)

其中：M，K，C分别为其质量、刚度和阻尼矩阵；F(t)为激振力。

对式(1)进行傅里叶变换得到

(2)

其中：ω为频率。

定义系统的动刚度矩阵

Z(ω)=K-ω2M+jωC

(3)

动刚度矩阵的逆矩阵即为系统的位移频响函数矩阵

H(ω)=Z(ω)-1=(K-ω2M+jωC)-1

(4)

其中：H(ω)为在频率ω下的位移频响函数矩阵，其元素Hij(ω)代表第j个自由度激励下第i个自由度的频率响应。

同理，可以得到系统的速度频响函数和加速度频响函数。

当系统参数θ存在不确定性的情况下，试验测试的频响函数和仿真计算频响函数有如下关系

He(ω)=Ha(ω;θ)+e

(5)

其中：He(ω)为试验频响函数；Ha(ω;θ)为仿真频响函数；e为二者的误差，它是一个随机变量。

2 贝叶斯框架下的模型修正

2.1 贝叶斯理论

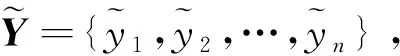
(6)

因此有

(7)

可以看出，当先验信息给定时，似然函数的值越大，参数的后验概率也越大，意味着该参数接近目标值的可能性越大。

2.2 适用于频响函数模型修正的似然函数

(8)

其中：e为实测值和仿真值的残差；Σ为协方差矩阵。

然而在实际情况中，受限于试验样本数量，其所服从的分布并不总能满足正态分布。另外，当在正态分布假设下选用频响函数数据直接进行修正时，必须选择少量频率点下的响应进行修正，否则可能出现响应数据的协方差矩阵奇异的情况，而不同的频率点选取策略则会对修正结果产生不同的影响[16]。近似贝叶斯估计是一种似然自由贝叶斯技术[23],该方法不假定数据服从某个特定的分布类型，而是通过设定一个容忍误差ε，并计算某个参数下模型数据和观测数据之间的距离d，当d<ε时，就接受该参数，否则拒绝该参数。基于该理论，笔者采用一种近似似然函数，以实现频响函数的不确定性模型修正。具体的似然函数表达式为

式(9)表明，当试验与仿真之间的误差满足试验本身的变异水平时，令似然函数值等于一个相对较大的数，而不满足时其值取零，从而实现对参数的接受和拒绝。同时为了保证继续搜寻其他满足收敛指标的参数而不停留在该处，故将似然函数设置成某个较大数附近的随机数，而非固定的值。

2.3 DREAM算法

对于参数后验概率的求解，由于Y关于θ的函数通常相对复杂或是以隐式存在，很难直接利用表达式进行积分计算，因此对于后验分布的求解一般借助于马尔科夫链蒙特卡洛(Markov chain Monte Carlo,简称MCMC)方法进行抽样。传统的MCMC抽样主要包括Metropolis算法、Metropolis-Hastings算法以及Gibbs抽样等，然而上述算法普遍存在计算效率低、拒绝率高及依赖建议分布严重的问题。后续发展起来的延迟拒绝MCMC算法能够自适应地改变建议分布，加快其收敛效率，但可能造成得到的后验分布与真实分布存在偏差。

DREAM算法[24]是一种改进的MCMC算法，其全称为差分进化自适应Metropolis算法。DREAM算法具备多链并行抽样的能力，每条并行链在产生不同初始样本后，通过差分进化方程来产生新样本，在搜索过程中能自适应地调整步长和方向，从而对多个全局最优区域进行有效搜索，有利于样本从局部最优点跳到全局最优点，拥有高效率的计算能力[25-26]。笔者采用 DREAM-Matlab工具箱[27]求解不确定性参数的后验分布。

本研究所提模型修正方法具体包含如下步骤：

1) 结合测试得到的频响函数数据，统计出所关注频率下的所有试验频响函数的上、下限以及中值；

2) 根据试验数据的上、下限及中值计算出数据的离散度，将其作为容忍误差向量；

3) 设定参数的初始范围及迭代次数；

4) DREAM算法抽样产生参数值，并代入模型计算频响；

5) 根据式(9)计算近似似然函数值L，若L>0则接受该参数，L=0则拒绝该参数；

6) 当计算次数小于等于设定的迭代次数时，回到步骤4，否则停止迭代计算，统计出所有使似然值取非零值的参数样本。

上述步骤的流程图如图 1所示。

图1 修正过程流程图Fig.1 The flow chart of model updating process

3 算例验证

3.1 三自由度算例

某三自由度振动系统见图 2，已知m1=m2=m3=1.0 kg，k3=k4=1.0 N/m，k6=3.0 N/m。其他3个刚度系数k1，k2，k5为待识别的不确定性参数，表现为在区间[0.8,1.2]N/m范围内波动。

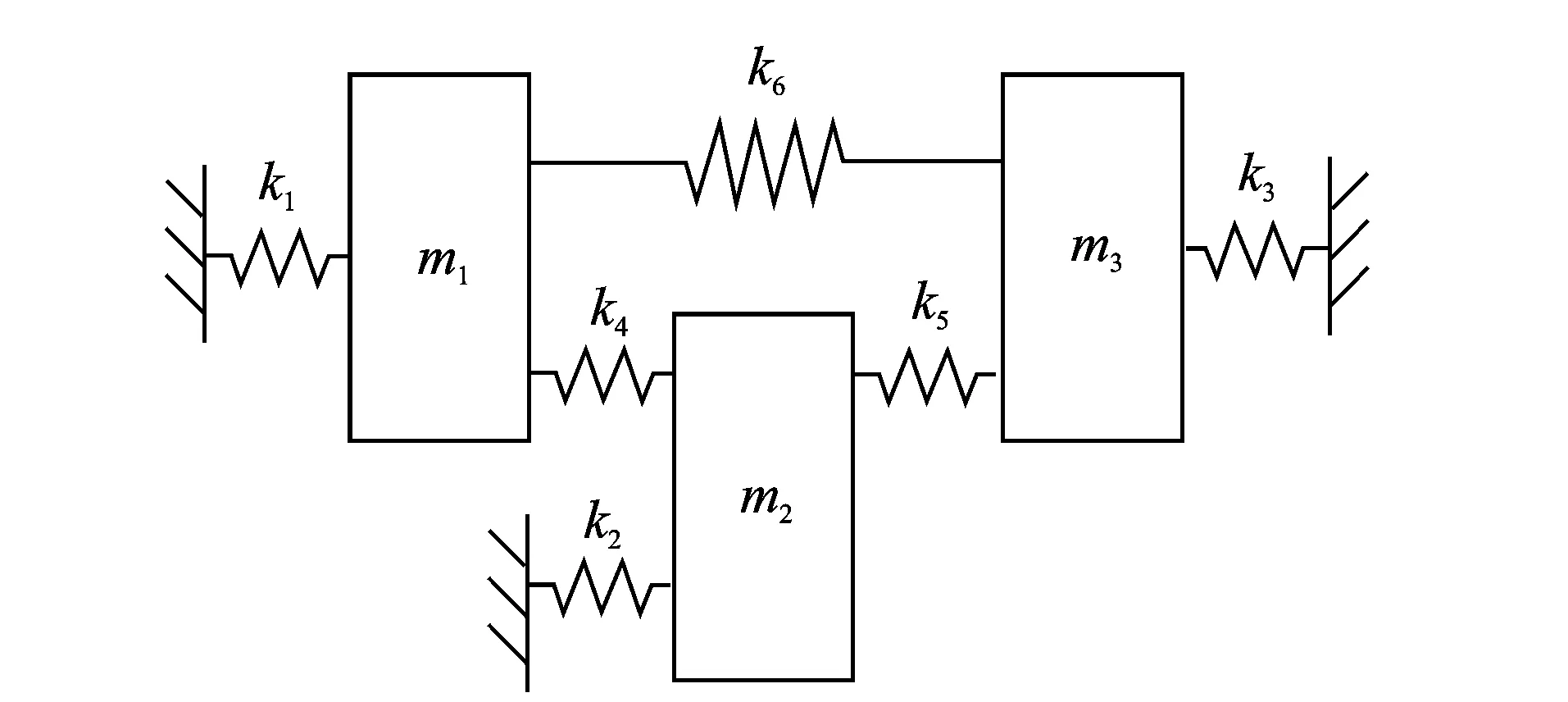
图2 三自由度系统Fig.2 3DOF vibration system

本算例在参数的目标区间范围内采用拉丁超立方抽样100次得到的频响函数作为目标值，认为参数的初始值在区间[0.4,2.4] N/m内，采用DREAM算法对参数的后验分布进行更新。图3给出了5 000次抽样计算的参数迭代结果，可以看出参数在约500次迭代后趋于收敛，将收敛后参数样本的最大值和最小值统计出来，并与目标值进行比较，结果见表 1。

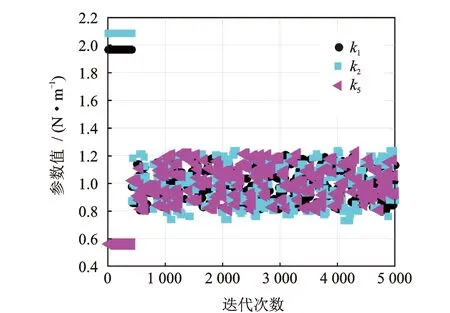
图3 待修正参数迭代收敛过程Fig.3 Iterative convergence process of modified parameters

表1 参数修正前后值及误差对比

从表1可以看出，修正后参数的上限值误差由原来的100%减小到3%以下，下限误差的绝对值由50%降低至不超过8.75%，可见修正效果显著。

图 4为修正前后频响函数的对比，分别给出了初始参数下得到的FRF值、目标FRF值和修正后的FRF边界值。从图 4可以看出，修正后FRF边界能够较好地包含所有的目标FRF曲线，相比于修正前，不确定性的范围大大缩小。

图4 修正前后FRF对比图Fig.4 Comparison of FRF before and after updating

3.2 H型非对称梁算例

结合某H型非对称梁有限元模型修正算例来说明笔者提出方法的可行性。H型非对称梁及其尺寸如图 5所示，将其划分为12个单元，材料为铝。在加工过程中，两侧的竖梁和横梁分别选用了两批不同的铝材料，同时由于安装过程中的损伤，其结构刚度受到了影响，主要体现在弹性模量的不确定性中，具体的材料参数见表2。

表2 材料参数及其不确定性

图5 非对称H型梁结构及其尺寸示意图(单位：mm)Fig.5 The unsymmetrical H-shaped structure(unit:mm)

本算例中选取E1和E2作为待修正参数，另外考虑系统阻尼的不确定性，将模态阻尼比也作为不确定性参数同时进行修正，采用Matlab和NASTRAN联合编程，在参数目标值范围内执行100次拉丁超立方抽样获得的频响函数作为目标值来代替试验。将参数的初始区间定义在[60 000, 80 000]MPa范围内。在图 5中标出的激励点处施加单位加速度激励，选取的频率带宽范围为100～800 Hz，模态阻尼比ζ的目标区间设定为[0.028,0.032]，初始区间为[0.02,0.04]。以图 5所示的响应点处的位移频响函数为目标，对参数进行修正。

表 3给出了参数修正前后的上、下限及误差对比，参数E1的误差由[-8.47%,10.42%]降低至[0.20%,0.79%]，参数E2的误差由[-8.47%,10.42%]降低至[0.29%,-0.11%]，参数ζ的误差由[-28.57%,25.00%]降低至[0.81%,0.41%]，表明参数的修正精度较高。图 6为修正前后的FRF对比图，分别给出了修正前后FRF边界以及目标值。可以看出相比于修正前，修正后的FRF边界缩小，并与目标值的边界相重合。图 7给出了其他响应点(单元10，11，12交点处节点)修正后FRF的预测对比，修正后的FRF边界与目标值的边界也基本吻合。进一步对所有试验测试的频响函数增加2%水平的高斯白噪声，以考虑试验噪声对修正结果的影响。参数修正结果见表4，可以看出，相比于修正前，不确定性参数的误差下降明显，修正后不确定性参数也接近于真实值，说明在一定水平噪声情况下，仍具有不错的修正效果。综上所述，笔者所提

表4 参数修正前后值及误差对比(2%噪声)

图7 其他响应点修正前后FRF预测对比图Fig.7 Comparison of FRF prediction before and after updating of other response point

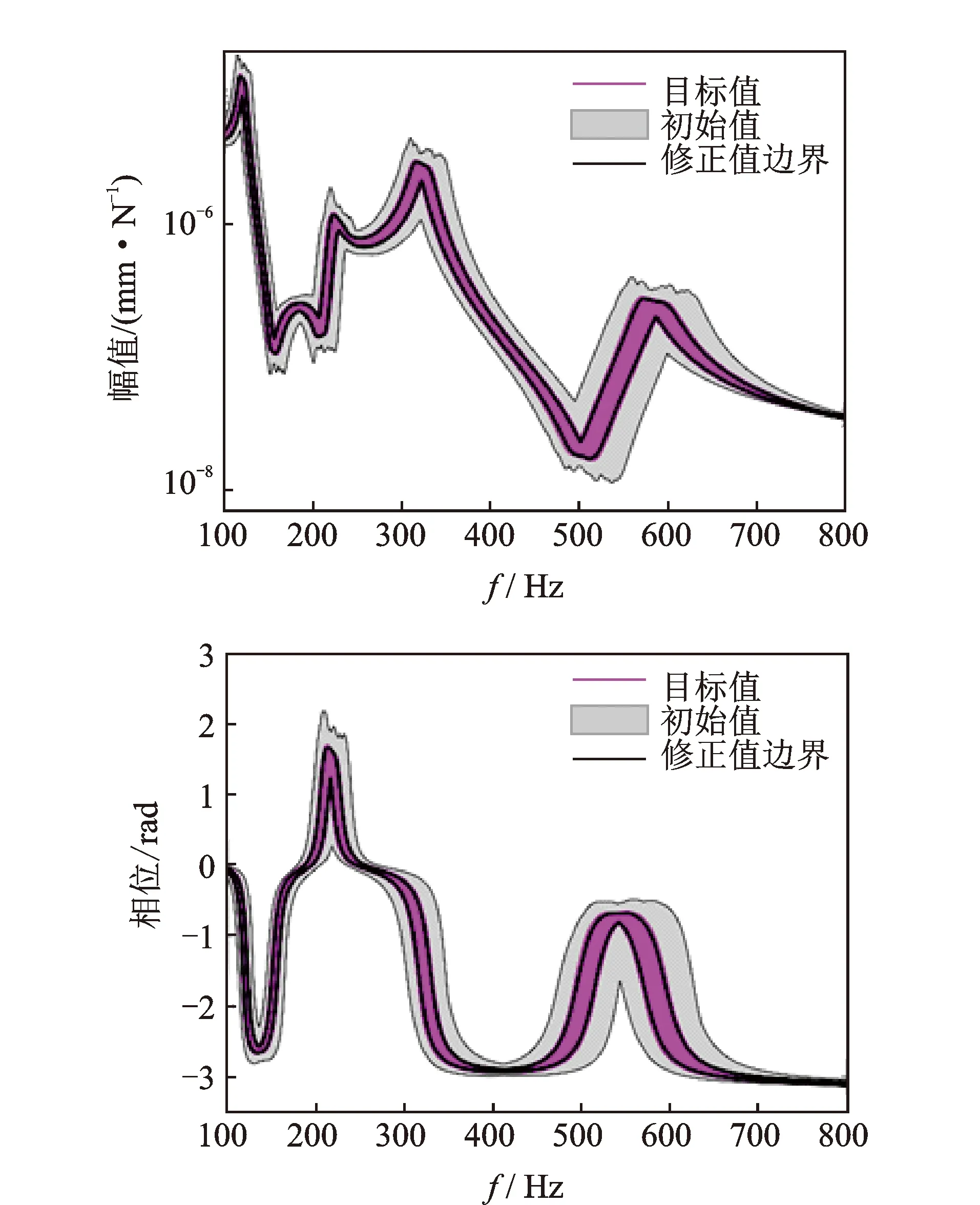
图6 修正前后FRF对比图Fig.6 Comparison of FRF before and after updating

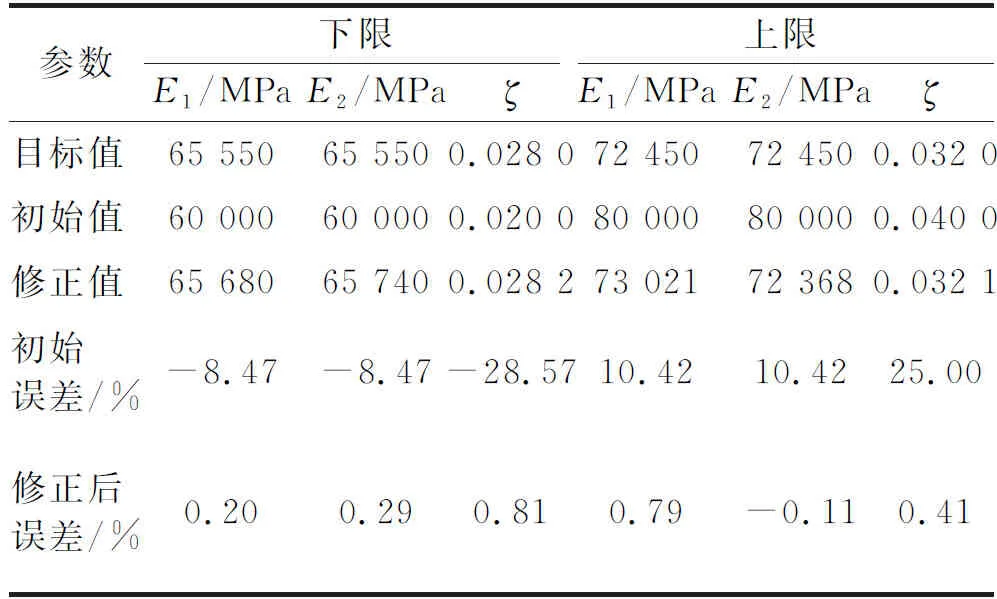
表3 参数修正前后值及误差对比

方法对有限元模型的不确定性参数修正也具有适用性。

4 结 论

1) 在贝叶斯模型修正框架下，引入近似贝叶斯计算方法，提出了一种近似似然函数，适用于频响函数不确定性模型修正，分别结合三自由度数值算例以及非对称梁的有限元模型修正算例进行了验证。

2) 修正过程中可直接应用离散化后的频响函数数据，不需要人为地选择频率点来避开共振峰处的响应。

3) 在参数分布不明确的情况下，采用区间来描述参数的不确定性，并引入近似贝叶斯计算理论，使用近似似然函数对参数进行筛选，避免了主观假设分布类型带来的偏差。

4) 算例结果表明，修正后的模型与目标值更加接近，且在一定噪声水平下仍能保持不错的修正效果，对于工程实际有一定的参考价值。