基于递归理论的泵站压力管道运行状态监测*

张建伟， 程梦然， 马晓君， 王立彬， 张翌娜

(1．华北水利水电大学水利学院 郑州，450046) (2．水资源高效利用与保障工程河南省协同创新中心 郑州，450046)(3．河南省水工结构安全工程技术研究中心 郑州，450046) (4．黄河水利职业技术学院土木与交通学院 开封，475004)

引 言

随着水利事业的蓬勃发展，大型梯级泵站的修建迅速展开，压力管道作为关键组成部分，其运行质量对整个系统的重要性不言而喻，因此，管道的安全稳定备受关注[1]。由于水力学条件的复杂性及结构自身动力特点，压力管道在不同运行状态下所受激励大不相同，导致水工结构存在不同程度的损伤累积和抗力衰减问题，进而引发安全事故。因此，面对压力管道为农业、石油、化工等方面带来巨大经济效益的同时，对结构采取安全监测，提高管道运行质量势在必行。

管道系统的组成部件较多，各元素之间相互干扰，大幅振动在所难免，一定程度上影响了管道的使用寿命[2]，因此关于管道健康检测的研究从未停止。早期的管道健康监测通过人力周期巡检完成。李宇庭等[3]利用场指纹法对金属管道缝隙的腐蚀状况进行监测，并证明了其在缺陷定位、测量上的优越性。杭利军等[4]利用分布式光纤法对管道泄漏进行监测，结果证实了该方法在实时管道监测和定位上的有效性。以上方法在管道安全监测方面成效显著，但大多存在价格昂贵、监测距离短、效率较低等问题，对长距离输水管道进行大范围、长时间的健康诊断困难较大[5]。近年来，随着我国综合技术的发展，新型的管道检测及监测技术逐渐崛起，如小波理论、希尔伯特-黄变换(Hilbert-Huang transform，简称HHT)等，但小波理论的应用局限于高频信号，辨识结果的完整度较低[6]。HHT变换中的坐标变换必然导致有效信息的丢失，进而影响分析结果，故寻找体积小、效率高、适用范围广的管道安全监测方法，成为状态监测领域的关注焦点[7]。

递归理论作为一种适用于非平稳、非线性信号的重要处理方法，具有处理过程简便、抗噪性强、对信号平稳程度要求较低等优点[8]。最先将递归图理论应用于实际的是生物医学领域。随后，生命科学、化学领域将其引入，用于信号处理。近年来，工程领域将递归图和递归量化分析应用于信号的消噪与分析过程[9-10]。为保证压力管道的稳定运行，避免大幅振动，笔者以数据级融合方式-方差贡献率为辅助，将递归理论引入到压力管道的状态监测中，对不同工况下的结构振测信号进行检测，并以递归图(recurrence plot，简称RP)、确定性(determinism，简称DET)、对角线平均长度L、递归率(recurrence rate，简称RR)以及递归熵(recurrence entropy，简称RE)等递归量化指标反映各工况下的信号特征，以监测管道振动状态，保证工程安全运行。

1 方差贡献率理论

基于方差贡献率[11]的数据融合方法，在汲取了传统融合方法[12-14]的优势后，为避免融合系数固定这一弊端，提出了系数动态化的融合方式。该方法不仅能减少单组错误数据导致的误诊现象，还可降低噪声与位置对单一传感器精度的干扰。此外，该方法的突出优势是：每一传感器所采数据的融合系数随时间而自动变化，增加了信号融合的普适性，并保证所采信号的完整性和准确性，同时提高了信号评价的有效性。具体步骤如下。

假定某一传感器在采样时间t内得到一组由离散信号值s(1)，s(2)，…，s(h)构成振测数据S(h)，定义点s(i)对此序列的贡献率为

Ki=(si-μ)2/hσ2

(1)

若p个同类传感器在同一时段内一同测得p组数据序列，各组序列包含h个数据点，令第p组数据中的第q个数据点的值为spq，由式(1)可知，spq对本组全部数据的贡献率为Kpq

(2)

若第p组数据序列的第q个数据spq分配到的融合系数为apq，则apq的求取公式为

(3)

融合后q点的值sq为

(4)

方差贡献率的数据融合过程如图1所示。

图1 基于方差贡献率的数据级融合流程图Fig.1 Flow chart of data fusion on the basis of variance contribution rate

2 递归图基本理论

2.1 递归图

递归图思想由递归图(RP)和递归量化分析(recurrence quantification analysis，简称RQA)两部分组成，以相空间重构为前提，其目的是用来展现时间序列的内在规律。

递归图具有可预测性，体现的是信号递归性，即一定时间段内某一结构运行特征的频发或复发，由大量黑白点及两条时间轴组成，并利用二维平面将这种递归性直观地展现出来，以定性的方式表示信号的时间平稳性。递归图具体建立方法如下

(i,j=1,2,…,N)

(5)

且有

(6)

其中：Ri,j为N×N方阵；N为状态向量xi的个数；ε为阈值；Θ(x)为Heaviside函数；‖xi-xj‖为Euclidean范数；m，τ分别为嵌入维数和延迟时间。

2.2 递归图模式

递归图存在不同的模式，每一模式都代表信号不同的演变规律，依据图形呈现的递归特性，从宏观和微观两个角度，便可定性得出信号特征。递归图模式及宏观分析见表1。

表1 递归图模式及其宏观含义

以上模式是对递归图的宏观分析，而针对图中点与线的分析则是从微观角度展开，具体研究对象及其含义见表2。

表2 递归图微观分析

2.3 递归量化分析

递归量化分析(RQA)是以各种递归指标，从不同侧面以定量的方式反映信号特征，主要包含以下几种参数。

1) 确定性(DET)：指主对角线上递归点的百分比，反映轨迹周期递归的程度，其值越小随机性越大，即

(7)

其中：P(l)为长度等于l的对角线的分布概率；lmin为最小对角线长度，一般为2。

2) 对角线平均长度(L)：指系统中两时间序列相互靠近的平均时长，又称平均预测时间，即

(8)

3) 递归率(RR)：在设定的阈值下，递归点在递归图中所有点的比例，系统动力特性越相似，RR值越大，即

(9)

4) 递归熵(RE)：指在递归图中与主对角线平行的线段长度分布的复杂性，其值越大表明系统的复杂性越大，即

(10)

递归理论对泵站压力管道的振动状态监测流程如图2所示。

图2 递归理论对泵站压力管道的状态监测流程图Fig.2 Flow chart of state monitoring of pressure pipe by recursion theory

3 工程实例

3.1 工程概况

甘肃景泰川工程，是一项分期建设的高扬程、大流量、多梯级电力提水灌溉工程，多年运行后，管道结构存有一定程度的损坏和老化问题，直接影响其运行安全。以景泰川二期七泵压力管道为研究对象，现场测点布置图及压力管道传感器放置点如图3所示。

图3 景泰川7泵压力管道现场测试及拾振器布置图Fig.3 Field test and measuring point layout of 7 pumping station in Jingtai Sichuan

3.2 振动信息采集

信息采集由安装在结构表面的传感器完成，为保证收集效果，泵站压力管道共放置了22个传感器。开关机组瞬间，压力管道的主支管连接处受水流激励和自身的激振力尤为复杂，因此，在连接处重点放置了3个速度传感器，分别为水平x方向、水平y方向和铅锤z方向，其他位置则分别布置了不同数量的传感器。管道振动测试激励以开关泵的方式获得，总体分为开关机瞬间与机组稳定运行期间两类振动状态，共划分为(A～K) 11种状态。各状态下的振测数据为连续采集，鉴于其时长过大，A～K工况为所测数据的代表性时间片段。

为全面反映各工况下管道振动特性，选取1～3号机开关瞬间均受影响较为明显的交叉口处的振测信号为研究对象，即以15，16和17号传感器(分别对应x,y,z三方向)在不同工况下所测信号的递归图与递归测度的变化为例，说明该方法对管道结构振动信号监测的有效性。具体实验工况如表3所示。

表3 管道原型试验测试工况

3.3 信息融合

为得到一组全面反映结构振动特性的综合信号，并简化对同一位置不同方向信号的监测过程，对15，16，17测点三方向信息实施递归图分析与递归量化分析之前，将其以方差贡献率的方式进行数据融合。以15，16，17测点在工况E状态下的融合效果为例，图4为x,y,z三方向及数据融合后的功率谱密度曲线。

图4 E工况下的振动信号功率谱密度曲线Fig.4 Power spectral density curve of vibration signal under E condition

3.4 参数m和τ的确定

相空间重构是绘制递归图、计算量化指标必不可少的部分，因此，选取合理的m和τ成为相空间重构的关键一步。采用伪近临法与互信息法分别选取相空间重构参数m和τ。恰当的维数m为相空间中伪近临点的百分比趋于零(至少小于5%)时对应的维数，且该维数之后，伪近临点百分比不再变动，最佳延迟时间τ为第1次达到最小值所对应的延迟时间，实测数据中m不小于2，τ不小于1。

经计算，景泰川二期七泵站压力管道在以上(A～K)11种状态下的相空间重构参数相差甚微，分别稳定在m=4，τ=4状态，限于篇幅，给出数据融合后工况E状态下参数选取图，如图5所示。

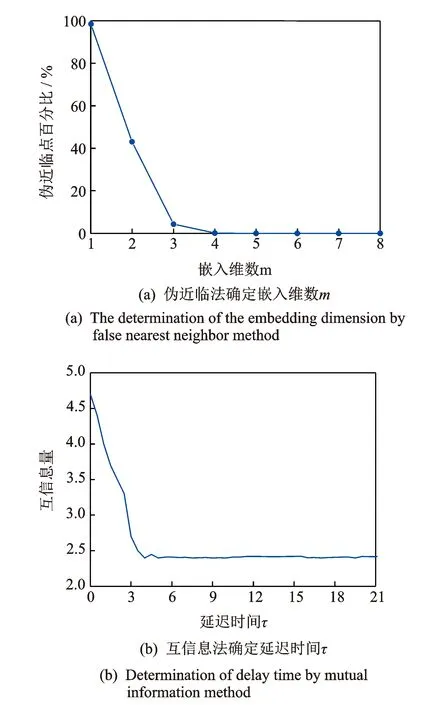
图5 相空间重构参数的选取Fig.5 The Selection of parameters for phase space reconstruction

3.5 基于递归图的状态监测

压力管道的运行状态总体分为开关机瞬间(B，D，F，H，J工况)与平稳运行(A，C，E，G，I，K工况)两大类状态，为检验递归图方法在压力管道不同振动状态下对信号的评估效果，分别从开机瞬间与稳定运行期间各选取一种工况绘制递归图。其中，嵌入维数m=4，延迟时间τ=4，阈值取融合后原始信号标准差的15%，递归图形态如图6所示。

图6 两种工况下压力管道振动信号递归图Fig.6 Recursive plot of vibration signal of the pipe under two operating conditions

由图6可知：D工况下的递归图中递归点汇聚成条状与块状，且分布较均匀，随时间变化在主对角线方向呈现一定规律，几乎不存在独立递归点，平行于主对角线的线段多且长，属于周期模式；E工况下的递归图的线条分布不均匀，独立递归点较多，平行于主对角线的线段模糊且较短，存在极为模糊的“十”字带状区域，属于飘移与突变的混叠模式。由此可知，两种工况下的振动信号均属于非平稳信号，相对于E工况，D工况振测信号的随机性差，确定性较强，呈现一定的周期性，复杂度较小。

3.6 基于递归量化指标的状态监测

递归图虽能直观辨别管道剧烈振动与平稳运行两种状态，但在图形识别上需要一定的经验，为此，在管道振动信号实施递归图识别的基础上，从周期性、非线性角度对信号进行量化分析。分别作出开关机瞬间(B，D，F，H，J工况)与平稳运行(A，C，E，G，I，K工况)两类状态的递归量化指标变化曲线，并将各指标浮动区间归一化，对比得出不同运行状态下的结构特征。

3.6.1 管道信号的周期性监测

图7为管道(A～K) 11种状态下的周期性指标变化曲线，由图可知：开关机瞬间，DET值位于0.97左右，L值位于0.72～0.98之间，管道信号的确定性较强，对角线平均长度较大；稳定运行期间，两值随管道振幅的减小而减小，DET位于在0.82左右，L值位于0.72～0.98之间，管道信号的确定性较差，对角线平均长度较小。两振动状态下管道信号的确定性指标DET相差约为0.15，最大差值为0.24；对角线平均长度L最大相差0.78。

图7 开关机瞬间与平稳运行两工况下的周期性指标对比图Fig.7 Index comparison diagram of periodicity under two types of working conditions

分析可知，周期性指标DET值与L值在管道剧烈振动与稳定运行两类状态下有明显差距，两者均能有效区分结构的振动状态，可作为管道振动状态监测中的参考指标。其原因是：泵机开关的短时间内，水体拍击与泵机振动均明显影响管道自身振动，促使管道振动呈现一定周期性，因此，信号的周期递归程度与平均预测时间增加，即DET值、L值增大；泵机稳定运行期间，水体拍击、泵机振动相对较弱，两者对管道的影响减小，进而结构振动信号的随机性升高，此时，信号的周期递归程度与平均预测时间降低，DET值、L值随之减小。

3.6.2 管道信号的非线性监测

管道结构在不同运行状态下，振动信号的非线性存在一定差异，因此，非线性指标递归率(RR)、递归熵(RE)也可作为监测结构振动特性的参考指标。图8中，开关机瞬间，RR值位于0.5左右,ENTR值稳定在0.35，系统振动的相似性较高，复杂度较低；随着泵机的稳定运行，水流对管道的激励减小，使系统振动的相似性降低，复杂度升高，RR值减小至0.05，RE值升高至0.88。两工况下信号的递归率RR最大相差0.5，递归熵RE最大相差0.53。

图8 开关机瞬间与平稳运行两类工况下的非线性指标对比图Fig.8 Index comparison diagram of nonlinear indexes under two types of working conditions

分析可知：在管道不同运行状态下，非线性指标RR值与ENTR值能以数值大小显示结构的振动幅度，当RR值偏高、ENTR值偏低时，说明结构振动较为剧烈；相反，则代表管道稳定运行。

根据前面递归图与递归量化指标在不同振动状态下的变化可知，排除人为及偶然因素后，若递归点随时间变化在递归图45°对角线方向呈现一定规律，且平行于该对角线的线段多且长，同时DET，L和RR三值均较大，而RE较小，说明此时管道结构的振幅偏大，其运行状态极有可能不利于自身的安全稳定。一段时间后，若递归图及各指标仍保持上述状态，应尽快检查管道安全，及时解决各种不利因素导致的异常振动。除检测管道损伤外，还可利用递归图与递归量化指标的敏感性，布置合理的管道转角，避免个别工况下的低频共振，监测泵站机组稳定性等。

4 结 论

1) 利用递归理论对管道的振动特性进行在线监测，相较于诸多学者提出的局限性较强的监测方法，更具有推广性和实用性。相较于利用诸多价格昂贵的机械设备对结构进行不定期检测的方法，经济性与自动化程度更高。

2) 将方差贡献率方法应用于压力管道的数据融合，能精准提取结构x,y,z三方向振动信号的特征信息，较大程度上提高了状态监测效率，且过程简单、快捷，在管道结构安全监测中有良好的实用性。

3) 递归图与递归量化分析皆能有效识别管道振动的剧烈程度，其中，递归图以不同的图形模式体现其振动程度，递归量化分析以各指标在0～1之间的不同幅值辨识管道振动状态。图形与指标分析相结合的监测方式，提高了状态识别的准确性，可推广至管道损伤诊断与在线监测领域。

4) 递归图与递归量化指标虽能有效监测管道运行状态，及时发现结构异常状态，但结构从“健康”到“不健康”发展过程中，图形及量化指标的变化状况并未涉及，有待进一步研究。