电动负载模拟器摩擦模型参数辨识方法*

李成成， 王广林， 潘旭东， 李跃峰

(1.兰州交通大学机电工程学院 兰州，730070) (2.哈尔滨工业大学机电工程学院 哈尔滨,150001)

引 言

负载模拟器是一种重要的半实物仿真设备，其主要功能是模拟飞机、火箭等飞行器舵机在测试中舵轴受到的期望力矩，从而实现在地面进行舵机各项技术指标检测的目的。负载模拟器能将具有破坏性的空中全实物检测转换为地面试验室中的半实物检测，从而达到的缩短舵机开发周期、降低开发成本和提高可靠性的目的。按照能量来源，负载模拟器可以分为电液负载模拟器、气动负载模拟器和电动负载模拟器。与其他两种负载模拟器相比，电动模拟器在小力矩情况下具有稳定性强、精度高和可靠性好等优点[1-3]。由于负载模拟器一般按照双向摆动状态运行，运行过程中所受摩擦力在动静摩擦力之间反复交替，因而对于具有高精度加载要求的电动负载模拟器而言，摩擦力的影响是不能忽视的。因此，为了提高电动负载模拟器的力矩加载精度，需要对其运行过程中受到的摩擦力影响的问题展开研究。

经典摩擦模型一般从静态角度推导运动速度与摩擦力的关系，主要方法包括Dahl模型[4]、Leuven模型[5]、LuGre模型[6]和Generalized Maxwell-Slip模型[7]等；然而上述模型都是不连续的摩擦模型。不连续的或者分段连续的摩擦模型会使控制器变的复杂且会增加系统的不稳定，不能满足负载模拟器高精度的力矩加载要求。因此，笔者引入一种连续可微的摩擦模型替代传统不连续摩擦模型。

Yang等[8]提出的CSA算法同PSO, GA等算法类似，都属于启发式的搜索算法，但是CSA算法较其他启发式算法具有先天的优势。CSA算法有效克服了上述启发式算法容易陷入局部最优的缺陷，提高了收敛速度，降低了计算量。近年来CSA算法被广泛应用在图像识别[9]、参数辨识[10]、控制理论[11]及医疗卫生[12]等领域，但是由于CSA算法的判定概率pa及搜索步长S在整个搜索过程中为固定数值，影响了CSA算法搜索性能的进一步提高。笔者针对电动负载模拟器运行过程中受到的摩擦力影响的问题，采用连续摩擦模型，提出一种改进CSA算法的电动负载模拟器连续摩擦模型参数辨识方法。该方法根据总的迭代次数和当前迭代次数自动调整判定概率pa和搜索步长S的数值，平衡了收敛速度和搜索精确度之间的矛盾关系，提高了CSA算法的收敛速度和搜索精度，并通过仿真和试验验证了该方法的有效性和准确性。

1 试验样机和数学模型

1.1 试验样机的建立

本研究进行参数辨识的数据来源于图1所示的试验台。该试验台为笔者自行设计的电动负载模拟器试验样机，其中：执行机构为伦茨永磁同步伺服电机MCS14L1，额定力矩为40 Nm，驱动器为伦茨配套的9400Highline，舵机为航天某所研制的弹用舵机，额定力矩为40 Nm，最大摆角为±30°；舵机角度传感器为雷尼绍RGH20圆光栅，与其配套使用的计数器板卡为研华PCI-1784，加载系统角速度由9400Highline驱动器反馈，扭矩传感器为北京中航科电ZH07；被加载舵机驱动器内置PID位置闭环控制器；工控机为研华IPC610L，模拟量输入输出分别采用研华PCL-818HD和研华PCI-1720。各个器件主要参数见表1。

图1 电动负载模拟器试验台Fig.1 Experimental setup of ELS

表1 试验样机的主要部件参数

1.2 数学模型

笔者采用永磁同步伺服电机作为电动负载模拟器的执行元件，驱动模式为电流反馈型脉宽逆变。在磁路不饱和、定子三相电流产生的空间磁势和转子磁通按正弦分布的理想情况下，不考虑转子磁场的凹极效应，并且永磁同步电机采用id=0控制模式的情况下，电动负载模拟器的动力学模型可描述为

(1)

其中：Jm为电机转子和加载轴的综合转动惯量，本研究中Jm取值为0.012 35 kgm2；Bm为阻尼和黏性摩擦因数；ωm为加载电机的角速度；Tl为扭矩传感器的输出力矩值；Tm为电机驱动力矩；Km为输入控制电压u和驱动力矩Tm之间的比例系数，Tm=Kmu，本研究Tm=0；Tf为库伦摩擦力值。

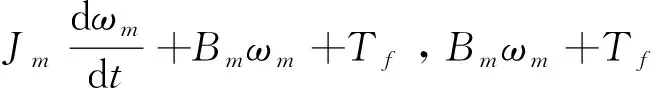
1.3 非线性连续摩擦模型

具有死区和库伦摩擦等明显非线性特点的系统在单一运行速度情况下可以用线性模型来表示[13]。但是，如果系统运行在双向摆动的状态下，且系统控制精度要求很高，那么系统死区和库伦摩擦的影响就不能被忽略。通过对目前的几种摩擦模型的分析，笔者选择一种连续可微的摩擦模型来描述负载模拟器运行过程中的摩擦特性。该摩擦模型主要是为了解决高精度控制系统中传统摩擦模型不连续造成的控制器不连续和系统稳定性差的问题[14]。该摩擦模型的表达式为

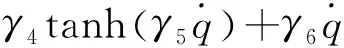
(2)

其中：γi∈R∀i=1,2,…,6为未知的正常数。

式(2)中所示的连续摩擦模型具有如下的特性：

1) 该摩擦模型为对称摩擦模型；

该连续摩擦模型共有6个待辨识参数，且为非线性模型。笔者采用启发式优化算法——CSA算法，将参数辨识问题转化为非线性系统优化问题[15]。

2 基于改进CSA算法的参数辨识

2.1 Lévy飞行机制的布谷鸟搜索方法

CSA算法的实质是布谷鸟如何通过Lévy飞行机制和寄生育雏的方式寻找到一个最优的鸟巢来免费孵化自己的卵。在自然界中，布谷鸟用一种随机的或者近似随机的方式来寻找寄生鸟巢的位置。为了模仿布谷鸟的这种搜索方式，在寻找鸟巢的过程中，有以下理想化假设：①每一个布谷鸟同时只产一个卵，且将它的卵放在一个随机选择的鸟巢中；②适合产卵的最好的鸟巢会被继承到下一代；③可供选择的鸟巢的数量是固定的，且布谷鸟所产的卵被鸟巢主人发现的几率为pa∈[0,1]。一旦卵被发现，鸟巢主人就会放弃这个鸟巢去建立一个新的鸟巢，这个卵也就被遗弃了，即所有的鸟巢都有pa的几率被替换为新的鸟巢[16-17]。

式(3)表示在算法中搜索下一代鸟巢位置的方式，以Lévy飞行机制产生下一代鸟巢的位置

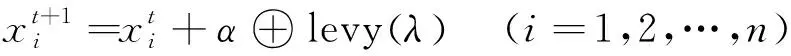
(3)

其中：运算符⊕表示逐次相乘；α>0为步长控制因子；levy(λ)为列维飞行机制。

旧鸟巢替换原则如下：选择一个服从均匀分布的随机数ε∈[0,1]，如果ε>pa，那么产生一个新的鸟巢替代旧鸟巢；否则，旧鸟巢被保留。

最优鸟巢判定原则如下：将每一个鸟巢输入目标函数，将使得目标函数值最小的那一个鸟巢作为本次最优鸟巢，并与所设定的迭代精度对比；如果目标函数值小于所设定的迭代精度，迭代结束；否则，继续下一次迭代优化，直到达到迭代精度或者完成迭代次数。

2.2 改进CSA算法

2.2.1 判定概率pa的调整策略

在CSA算法中，是否产生一个新的鸟巢是由随机数ε和判定概率pa共同决定的，因此最终的优化结果是受到判定概率pa的影响。笔者通过多次试验和计算发现：如果pa太小，算法收敛速度加快但很难收敛到最优解；相反，如果pa过大，算法的收敛速度缓慢。根据这一规律，应该在优化前期取较小的pa加快收敛速度，优化后期取较大的pa提高搜索精度。笔者提出了如式(4)所示的pa调整策略

pa(t)=pa,max+(pa,min-pa,max)e-r1(t/tmax)p1

(4)

其中：pa,max和pa,min为判定概率的最大值和最小值，分别取0.75和0.05；t为当前迭代次数；tmax为最大迭代次数；r1为限制因子，本研究取值为10；p1为一个整数，本研究 中取值为10。

2.2.2 迭代步长S的调整策略

通过分析CSA算法可以发现，迭代步长S对算法能否达到全局最优解及设定的搜索精度起到关键的作用。较大的迭代步长能够帮助算法跳出局部最优，同时也会降低搜索精度和收敛速度；相反，较小的迭代步长容易获得局部最优解。因此，关键点是如何找到一个合适的迭代步长以避免获得局部最优，同时提高收敛速度和搜索精度。笔者提出了如式(5)所示的迭代步长调整策略

S(t)=Smin+(Smax-Smin)e-r2(t/tmax)p2

(5)

其中：Smin和Smax分别为迭代步长的最大值和最小值，分别取0.01和0.5；r2为限制因子，本研究取值为100；t为当前迭代次数；tmax为最大迭代次数；p2为一个整数，本研究取值为10。

2.2.3 标准函数的仿真测试

为了验证笔者提出的改进CSA算法的有效性，进行了仿真验证测试。选取7个常用的全局最优测试函数进行仿真验证，这7个测试函数分别如下:

1) Schwefel 函数

(-500≤xi≤500)

2) Rosenbrock 函数

(-2.048≤xi≤2.048)

3) Griewank 函数

(-600≤xi≤600)

4) Rastrigin 函数

(-5.12≤xi≤5.12)

5) Sphere 函数

6) Drop-wave 函数

(-5.12≤xi≤5.12)

7) Branin 函数

(-5≤x1≤10,0≤x215)

Schwefel 函数在其定义域内有许多局部最小和一个全局最小值f1(X*)=0,X*=420.968 7,…,420.968 7；Rosenbrock 函数有一个全局最小值f2(X*)=0,X*=1,…,1；Griewank 函数有许多规则分布的局部最小值和一个全局最小值f3(X*)=0,X*=0,…,0；Rastrigin 函数有很多规则分布的局部最小值，Sphere 函数有n个局部最小值，且这两个函数具有相同的唯一全局最小值f4(X*)=f5(X*)=0,X*=0,…,0；Drop-wave 函数有一个全局最小值f6(X*)=-1,X*=0,0；Branin 函数有3个相同的全局最小值f7(X*)=0.397 887,X*=(±π,2.275),(9.425,2.425)。

测试的目的是利用ICSA和CSA算法搜索所有7个测试函数的全局最小值，并对2种算法搜索过程的指标进行对比。测试中传统CSA的参数设置为：鸟巢个数n=25；判定概率pa=0.25；步长S=0.03。ICSA参数见式(4)和式(5)。2种算法分别运行30次，且当迭代到达150次时停止。

图2为7个测试函数的某次仿真测试曲线，从图中可以看出，ICSA算法比传统CSA算法的收敛速度更快，收敛精度更高。

图2 ICSA和CSA算法的搜索曲线Fig.2 Search curves of ICS and CS algorithms

表2为7个测试函数在应用2种算法的情况下运行30次搜索运算所获得的最优解、解的平均值及方差的具体数值。对比表2中的仿真结果可知，CSA算法和ICSA算法均能成功获得全局最小值，但是ICSA算法获得的最优解和解的平均值更准确。通过计算30次运算结果的方差可知，ICSA算法的稳定性更好。

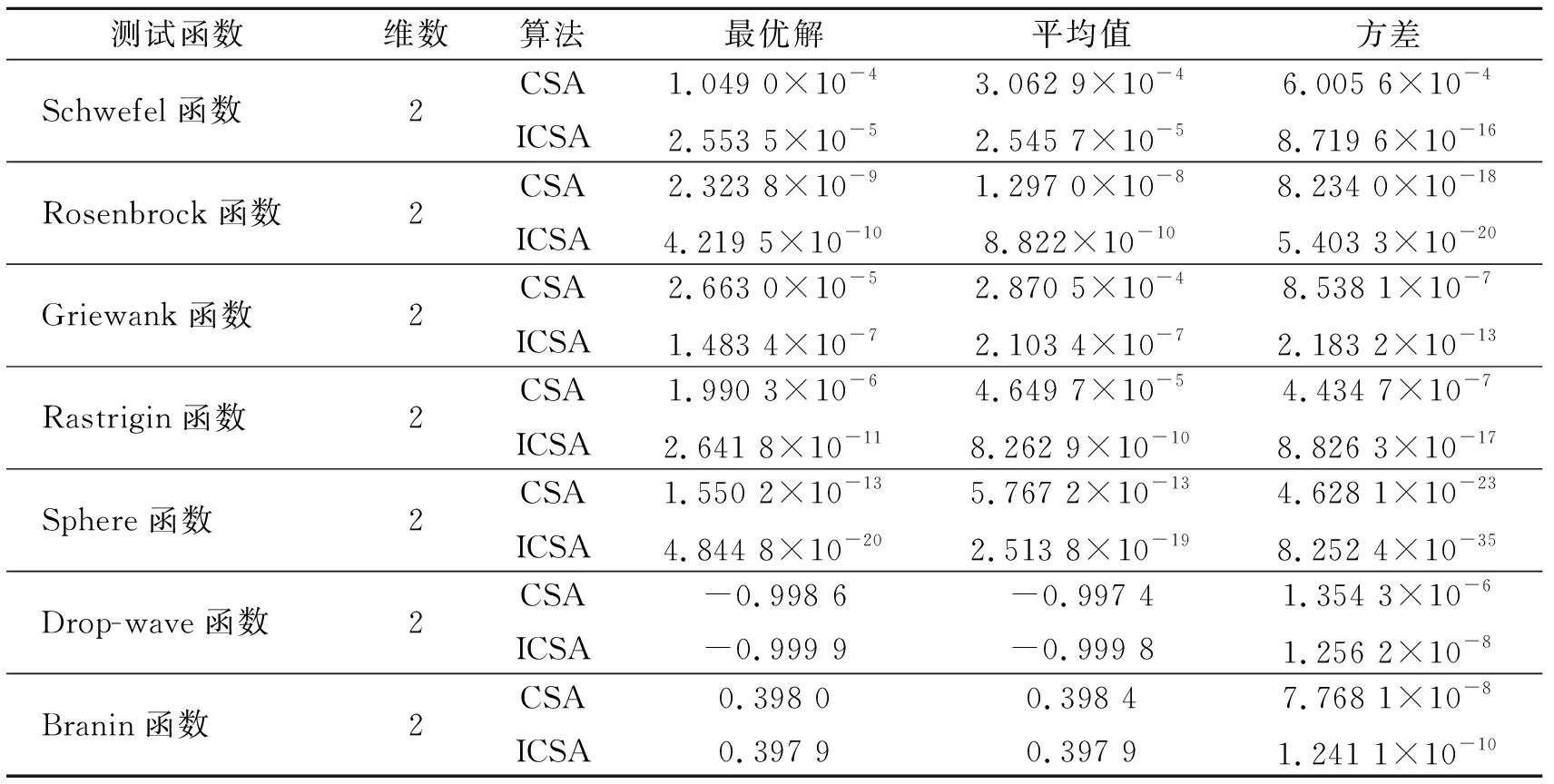
表2 不同方法获得的解的对比

2.3 连续摩擦模型的参数辨识

2.3.1 摩擦力测量试验

连续摩擦模型的参数是通过对电动负载模拟器的角速度-摩擦力曲线的辨识得到。本研究中的速度-摩擦力曲线是通过具体试验获得的。在试验中，舵机由专门的PID闭环控制器控制，能保证运行过程中的角速度准确跟随输入指令。

通过式(1)可知，当舵机按照某一角速度指令匀速运行时，转动惯量的影响被消除且负载模拟器空载运行，此时记录当前传感器的输出值，即为当前摩

擦力的值。因此，舵机按照一系列的角速度指令分别做匀速运动，记录这些速度对应的摩擦力值，即可得到电动负载模拟器的速度-摩擦力曲线[18]。

在本研究中，舵机的角速度取值范围为[-1,1] rad/s，共进行100组试验，正负两侧各50组。为了能比较准确的反映摩擦模型的特性，在角速度为0～0.1 rad/s的范围内进行25组试验，其余25组试验在角速度为0.1～1 rad/s的范围内进行。负角速度方向对称地进行上述试验。

将得到的100组试验数据进行多项式曲线拟合得到的结果如图3所示，拟合曲线近似描述了电动负载模拟器角速度与摩擦力对应的关系。

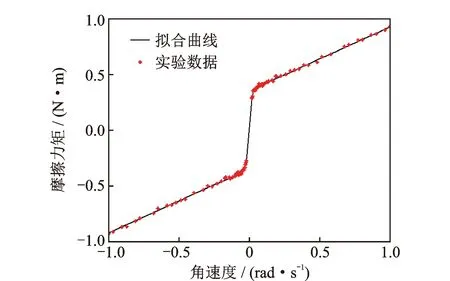
图3 摩擦力试验数据和拟合曲线Fig.3 Experimental data and fitting curve of friction

2.3.2 目标函数的确定

根据式(2)可知，本研究需要辨识的连续摩擦模型的模型结构是已知的，因此参数辨识问题转化为优化问题，优化的目的是系统输出和模型输出的差值使得目标函数的函数值最小。因此，需要设计一个适合辨识模型的目标函数，使得该函数能够描述模型输出逼近系统测量输出的程度。

待辨识的连续摩擦模型参数包括6个，定义这6个需要辨识的参数为：Ξ=[γ1γ2γ3γ4γ5γ6]T∈R6。定义逼近误差为

(7)

其中：Tf[ωi]为负载模拟器以ωi的恒定速度运行时传感器输出力矩(摩擦力的值)；Tfs[Ξ,ωi]为负载模拟器以ωi的速度运行时，根据当前辨识参数Ξ，通过连续摩擦模型计算得到的摩擦力值。

本研究定义的目标函数如下

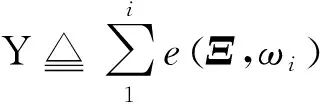
(8)

2.3.3 参数辨识结果及分析

为了说明ICSA算法对非线性模型参数辨识的有效性及其较CSA算法的优势，笔者分别设计了以下2组试验：①以CSA算法为搜索方法进行辨识试验；②以ICSA算法为搜索方法进行辨识试验。2组试验分别运行30次并计算平均值，其中CSA算法和ICSA算法的参数选择如表3所示。

表3 CSA算法和ICSA算法的参数选择

表4列出了运行30次的ICSA算法和CSA算法的参数辨识结果的平均值。

图4为某次运算的CSA和ICSA对比曲线，其中：黑色实线表示传统CSA算法搜索过程中目标函数与迭代次数的关系曲线；红色实线表示ICSA算法搜索过程中目标函数与迭代次数的关系曲线。不难看出，在迭代进行的前25次中ICSA算法能快速地收敛到最优解附近，而传统CSA算法在迭代进行到75次左右时，才收敛到与ICSA算法25次迭代附近相同的目标函数值。当迭代进行到最大迭代次数300次时，ICSA算法比传统CSA算法具有更高的收敛精度。由表4可知，进行30次辨识运算获得的ICSA算法的目标函数值的平均值较CSA算法的目标函数值的平均值减小了45.2%。因此，ICSA算法比CSA算法收敛速度更快，且收敛精度更高。

表4 参数辨识结果

图4 某次运算中ICSA算法和CSA算法的目标函数值Fig.4 Objective function value of ACSA and CSA in one time

2.3.4 辨识结果验证试验

上节的试验得到了各个参数的具体数值，这些数值是否是系统参数的真实值还需要进行进一步的验证。虽然这些参数不能通过试验的方式直接获得，但是只要能验证利用这些辨识的参数得到的系统估计输出和系统测量输出吻合，就能证明辨识得到的参数是系统的真实值。

笔者设计了以下的验证试验：首先，舵机按照最大速度0.04 rad/s、频率1Hz的正弦规律运动，即w=0.04sin(2πt) rad/s，试验样机数据采样时间为0.001 s。由于加速度引入的力矩为0.003 1 Nm，远远小于摩擦力的大小，可忽略，因此认为此时传感器输出的扭矩值全部为系统摩擦力；其次，将得到的各个系统辨识参数带入连续摩擦数学模型中，同时确保摩擦模型的输入与实际系统的输入相同，然后计算出摩擦力的估计值。图5中黑色实线表示系统实际的摩擦力测量值，红色实线表示利用ICSA算法得到辨识参数的摩擦力估计值，蓝色实线表示利用传统CSA算法得到辨识参数的摩擦力估计值。从图中可以看出，当舵机运动速度在零速度附近时，ICSA算法和CSA算法的摩擦力估计值都能与测量值很好地吻合，但当舵机运动速度在最大速度附近时，ICSA算法的摩擦力估计值能很好地与测量值吻合，而CSA算法的摩擦力估计值与测量值误差较大，因而证明了所设计的ICSA算法能更准确地获得摩擦模型的各个参数。

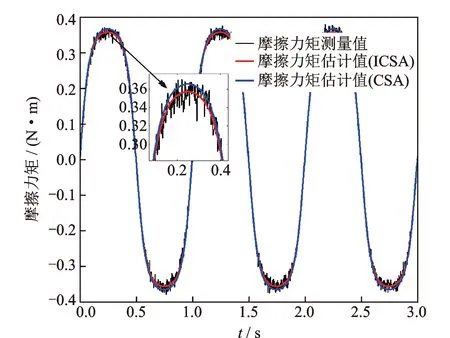
图5 验证试验结果Fig.5 Experimental verification

3 结 论

1) 电动负载模拟器具有较高的控制精度要求，传统的不连续的摩擦模型不利于负载模拟器高精度控制器的设计。为解决这个问题，引入了连续可微的摩擦模型，并针对该模型提出了改进的CSA算法的参数辨识方法。

2) 利用提出的ICSA算法进行辨识试验，获得了非线性摩擦模型的6个参数的数值。对30次搜索结果求平均值发现，ICSA算法的目标函数值较CSA算法减小了45.2%。通过试验验证了所提出的ICSA算法较大地提高了摩擦模型参数辨识的精确度和收敛速度。

3) 文中给出的判定概率pa和步长S的调整策略仅仅表达了在辨识过程中pa和步长S变化趋势对CSA算法收敛速度及收敛精度的影响，其具体数值并不一定是最优值，更优化的调整策略有待进一步的研究。