二自由度七连杆机器人腿部机构优化设计
罗中华
(上海建桥学院机电学院,上海 201306)
工业机器人产业是中国智能制造领域的突破口和重要抓手,被誉为“制造业皇冠顶端的明珠”,其研发、制造、应用是衡量一个国家高端制造业水平和科技创新能力的重要标志[1-2]。移动机器人是机器人的一种类型,由计算机控制,具有移动、自动导航、多传感器控制、网络交互功能等。按运动方式的不同,移动机器人可分为轮式、履带式和足式机器人等,相比于轮式和履带式机器人,足式机器人对复杂地形和非结构化环境具有更强的适应性[3-4]。移动机器人广泛应用于各个领域,在食品领域的应用包括食品加工、包装、分拣及码垛。在食品领域机器人中,应用多连杆机构和凸轮机构比较多[5-7]。随着美国波士顿动力公司设计、制造的系列足式移动机器人的大规模应用,可移动式机器人的发展已进入了新时期。其应用范围拓展到了军事、灾害救援、地质勘探、核事故抢险、生活服务等领域[8-9]。
多连杆机构广泛地应用于移动机器人腿部机构,目前已有单腿、双腿、4腿、6腿和8腿足式机器人[10]。腿部运动机构是机器人实现预定动作及轨迹的关键部件之一[11],有较多学者[12-14]对腿部运动机构的尺寸参数进行了优化设计。但现有移动机器人腿部多连杆机构的优化设计研究不够完善,主要体现为优化设计的目标函数不够准确、约束条件不完整等,导致现有优化的多连杆机器人腿部机构足端的实际轨迹曲线与理想轨迹曲线误差较大。
章永年等[13]对二自由度七连杆(文中称五连杆机构,实际为七连杆机构)机器人腿部机构进行了研究,优化设计的目标函数是关节电机力矩性能、节电机速度性能、电机的总能耗、五杆总长最小;试验仅选取了3个机构参数作为设计变量、10个约束条件,根据此约束条件不能保证机器人腿部足端点实现预先给定的理想轨迹曲线。由于没有给出驱动摆杆的摆动角度范围以及如何摆动,无法验证试验机器人腿部足端点的实际轨迹曲线。
为了使机器人腿部足端的实际轨迹曲线与预先给定理想轨迹曲线尽量重合,试验拟对章永年等[13]研究的二自由度七连杆机器人腿部机构优化设计进行了适当改进。增加两个机构角度尺寸参数;设计变量选用全部机构参数以及驱动曲柄ED与x轴的初始夹角αs、驱动摇杆AF与x轴的初始夹角βs和摇杆AF旋转角度δ等16个参数;目标函数是使足端相对实际轨迹曲线上k个点(优化数例k=72)到足端相对理想轨迹曲线的最小距离的代数和最小;建立包含几何约束、性能约束和变量的上、下限约束等42个约束条件。以椭圆曲线作为机器人腿部足端相对理想轨迹曲线、驱动摇杆的来回摆动采用STEP运动函数,对二自由度七连杆机器人腿部机构进行优化设计。利用优化的七连杆机器人腿部机构,设计了6足仿真机器人,并采用UG软件对优化的七连杆机器人腿部机构和6足仿真机器人进行运动仿真。旨在为了验证七连杆机器人腿部机构优化设计的正确性和应用于6足机器人的可行性。
1 运动公式
七连杆机器人腿部机构如图1所示[13]。七连杆机器人腿部机构活动构件数n=6、低副数PL=8、高副数PH=0,机构的自由度为2。驱动曲柄为杆DE、驱动摇杆为杆AF。为了便于后面机构优化,坐标原点未放在铰链点上。七连杆机构尺寸参数包括机构的杆长参数l1、l2、…、l7,铰链点A、E的坐标分别为(xA,yA),(xE,yE),构件的角度参数θ和φ,以及驱动曲柄ED与x轴的初始夹角αs、驱动摇杆AF与x轴的初始夹角βs和摇杆AF旋转角度δ。

图1 七连杆机器人腿部机构图
设曲柄DE从初始角θ逆时针旋转α(逆时针方向为正,下同),则D点坐标为:
(1)
设摇杆AF与x轴的夹角为β(β∈[βS,βS+δ]),则F点坐标为:
(2)
B点坐标为:
(3)
设摇杆DB与x轴的夹角为φ,则有:
(4)
设摇杆DC与x轴的夹角为φ1,则有:
(5)
其中,
C点坐标为:

(6)
H点坐标为:
(7)
设摇杆FH与x轴的夹角为φ2,则有:
(8)
设摇杆FG与x轴的夹角为φ3,则有:
(9)
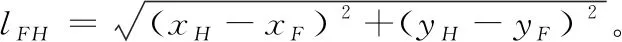
G点坐标为:
(10)
设摇杆HG与x轴的夹角为φ4,则有:
(11)
I点坐标为:
(12)
2 机构优化设计
2.1 足端理想轨迹曲线
现有文献[4,14-15]常见的机器人足端理想轨迹曲线有矩形曲线、椭圆、抛物线、摆线(修正摆线)、心形线、组合线段等。这些足端理想轨迹曲线中,有封闭曲线和非封闭曲线两种。机器人腿部按足端是否与地面有相对运动分为摆动相和支撑相。支撑相的腿部足端相对于地面是静止不动的,而支撑相腿部机构的其他部位是运动的,从而推动机器人机身向前运动。同时,摆动相的腿足端的绝对运动是机器人机身的牵连运动和足端相对于机器人机身的相对运动的合成运动。按机身是否运动,将机器人腿部足端轨迹曲线分为相对轨迹曲线和实际轨迹曲线。当驱动曲柄旋转一周,足端相对轨迹曲线一定是一条封闭的曲线,足端实际轨迹曲线一定是一条非封闭的曲线。因此,机器人腿部机构优化设计时,足端理想轨迹曲线应分为相对理想轨迹曲线和实际理想轨迹曲线,足端实际轨迹曲线应分为相对实际轨迹曲线和实际轨迹曲线。
在机构优化设计时,很难求得机器人机身的牵连运动和腿部足端的实际轨迹,因此,对机构优化设计时,足端理想轨迹曲线选用相对理想轨迹曲线。定义机器人左右两边、前后同一位置的两条腿分别为A腿和B腿。当足端相对理想轨迹曲线为椭圆曲线时,并假设上半个椭圆曲线和下半个椭圆曲线准确地分别为摆动相和支撑相,图2为机器人腿部机构足端的实际理想轨迹曲线。理论上,跨障高度为椭圆短半轴的2倍,机器人单步步长为椭圆长半轴的4倍。但实际上,因为连杆机构基本上不能准确地使上半个椭圆曲线和下半个椭圆曲线分别为摆动相和支撑相,实际步长与理论步长存在一定误差。

双点画线的椭圆曲线为足端的相对理想轨迹曲线;B点为B腿的立足点,实线为A腿足端的实际理想轨迹;A点为A腿立足点,虚线为B腿足端的实际理想轨迹曲线
2.2 优化设计数学模型
2.2.1 设计变数 选取二自由度七连杆机器人腿部机构全部16个参数作为优化设计变数,即
X=(x1,x2,…,x16)T=(l1,l2,l3,l4,l5,l6,l7,xA,yA,xE,yE,θ,φ,αs,βs,δ)T。
(13)
2.2.2 目标函数 二自由度七连杆机器人腿部机构的优化设计的目标是使足端相对实际轨迹曲线尽量与足端相对理想轨迹曲线重合。选用足端相对实际轨迹曲线上k个点到相对理想轨迹曲线的最小距离的代数和最小作为七连杆机构优化设计的目标函数[16],即
(14)
式中:
di——足端相对实际轨迹上的第i个点到足端相对理想轨迹曲线的最小距离。
2.2.3 约束条件 机构应满足几何约束条件和传动角约束条件。根据七连杆机器人腿部机构尺寸参数,建立二自由度七连杆机器人腿部机构的约束条件为:
lBDmax≤x3+x4,x3≤lBDmin+x4,x4≤lBDmin+x3;
lFHmax≤x2+x6,x2≤lFHmin+x6,x6≤lFHmin+x2;
(15)
式中:
lBDmin、lBDmax——点B与D之间的最小和最大距离;
lFHmin、lFHmax——点F与H之间的最小和最大距离;
γmin——机构的最小传动角。
设各变量下限值ximin和上限值ximax,变量下限和上限约束条件为:
ximin≤xi≤ximax(i=1,2,…,16)。
(16)
综上,二自由度七连杆机器人腿部机构优化设计为16个设计变量、42个约束条件的约束优化设计问题。二自由度七连杆机器人腿部机构优化设计的标准形式为:
(17)
2.3 遗传算法
遗传算法(GA)是美国Michigan大学John Holland教授1975年首先提出、基于1858年达尔文的自然选择原理、自然遗传机制、优胜劣汰和适者生存的生物遗传和进化的规律而形成的一种随机搜索优化算法。该算法的主要步骤[17]:
① 随机产生一组初始个体构成初始群体;
② 计算群体中个体的适应度;
③ 判断算法收敛准则是否满足,若满足则输出搜索结果并停止运算,否则转下一步;
④ 选择运算,按优胜劣汰执行复制操作;
⑤ 交叉运算,按一定的方式进行交叉操作;
⑥ 变异运算,按一定的规律执行变异操作;
⑦ 转步骤②。
2.4 数例
取足端相对理想轨迹曲线为长半轴100 mm、短半轴40 mm的椭圆曲线,椭圆的中心为坐标原点。机构的最小传动角γmin=30°,各变量下限和上限取值约束为:30 mm≤l1≤50 mm、20 mm≤l2≤40 mm、30 mm≤l3≤90 mm、120 mm≤l4≤220 mm、15 mm≤l5≤60 mm、100 mm≤l6≤160 mm、140 mm≤l7≤180 mm、10 mm≤xA≤35 mm、220 mm≤yA≤400 mm、10 mm≤xE≤25 mm、200 mm≤yE≤380 mm、120°≤θ≤250°、100°≤φ≤180°、0°≤αS≤360°、210°≤βS≤270°、20°≤δ≤70°,相对实际轨迹上取k=72个点。驱动曲柄采用匀速转动,即ω=-180°/s,经驱动摇杆分别采用匀速往复摆动和STEP运动函数往复运动对机构进行优化设计,发现STEP运动函数往复运动优化设计效果好,故驱动摇杆采用STEP运动函数[18],即STEP(time, 0, 0, 1,δ)+STEP(time, 1, 0, 2, -δ)。选用遗传算法作为优化方法,编写二自由度七连杆机器人腿部机构优化设计程序。用编写的优化设计程序求得的七连杆机器人腿部机构的最优解为l1=44.654 mm、l2=38.360 mm、l3=84.848 mm、l4=120.005 mm、l5=44.498 mm、l6=119.231 mm、l7=150.672 mm、xA=10.328 mm、yA=296.586 mm、xE=19.729 mm、yE=355.336 mm、θ=193.475°、φ=134.729°、αs=118.259°、βs=210.128°,δ=42.5304°,f(X*)=29.061 9 mm。优化的七连杆机器人腿部机构运动仿真如图3所示。驱动曲柄每1°为一个等分点进行仿真,足端最大、最小的x坐标分别为100.035 mm和-100.036 mm,足端最大、最小的y坐标分别为40.005 mm和-40.009 mm,与理想的椭圆的长、短轴半径的最大相对误差仅为0.036%。足端的实际轨迹平均每点与理想椭圆轨迹曲线的绝对误差约为0.40 mm,最大误差的点的绝对误差约为1.45 mm。从图3可以看出,优化的七连杆机器人腿部机构足端相对实际轨迹曲线几乎完全与相对理想轨迹曲线重合。因此,文中七连杆机器人腿部机构的优化结果是十分理想的。
设A腿和B腿的七连杆机构曲柄相位角相差180°,当A腿和B腿的两足端的y坐标相等时,两腿的两足端与地面接触,随后一腿为支撑相,另一腿为摆动相。根据A腿和B腿足端的仿真数据,采用Excel绘制优化的七连杆机器人腿部机构两腿足端的实际轨迹曲线如图4所示。由图4可知,机器人实际步长约为393.9 mm,跨障高度约为80 mm。步长略小于400 mm的主要原因是两腿足端的y坐标相等时,y不为零(y=6.023 mm)所致。即足端支撑相和摆动相,机构的曲柄不是各转180°所致。

椭圆曲线为相对理想轨迹曲线、用双点画线表示,符号“+” 为机器人腿部足端相对实际轨迹点

实线为A腿足端的实际轨迹曲线,虚线为B腿足端的实际轨迹曲线
3 6足仿真机器人设计
以优化的二自由度七连杆机器人腿部机构尺寸参数为依据,设计了6足仿真机器人。文中所谓仿真机器人是指只考虑运动分析正确性的机器人,而不考虑具体机构的结构设计和提供驱动的动力装置。6足仿真机器人如图5所示,其3条腿为一组。将3条腿固定于下机身固定板,如图5(a)所示,另3条腿固定于上机身固定板,如图5(b)所示。上、下机身固定板用转动副连接,使机器人具有转弯的功能,完整的6足仿真机器人如图5(c)所示。

图5 6足仿真机器人
当一组3条腿为摆动相时,上、下机身固定板之间的转动副相对转动,使摆动相3条腿的固定板向左或向右转过一定的角度;当摆动相3条腿变为支撑相时,转动副再相对转动,从而实现6足机器人转弯功能。
A腿和B腿七连杆机器人腿部机构曲柄相位角相差180°,由图6可知,一组腿完成一个单步步长约400 mm,另一组腿完成一个单步步长约400 mm,与优化设计的单步步长非常吻合,说明6足仿真机器人运动仿真结果可靠。

数字0,400,800表示地板位置尺寸,单位:mm
4 结论
推导了二自由度七连杆机器人腿部机构运动分析计算公式,并建立了二自由度七连杆机器人腿部机构优化设计数学模型;以椭圆曲线作为相对理想轨迹曲线,对具体的二自由度七连杆机器人腿部机构进行了优化设计。优化的七连杆机器人腿部机构足端相对实际轨迹曲线几乎与相对理想轨迹曲线完全重合,优化结果十分理想,能较准确地实现机器人预定的步长和跨高。试验机构优化设计追求的是使足端相对实际轨迹与相对理想轨迹尽量重合,而足端实际轨迹与实际理想轨迹尽量重合有待进一步研究。此外,调整两组腿部机构的曲柄不是相差180°,而是使整个机器人的足端支撑相和摆动相曲柄各转180°,从而消除用足端相对实际轨迹与相对理想轨迹尽量接近作为目标函数所引起的误差。

