SM4密码算法的阶梯式相关能量分析

2020-08-06 08:28韦永壮刘争红

计算机应用 2020年7期

丛旌，韦永壮*，刘争红

（1.广西密码学与信息安全重点实验室（桂林电子科技大学），广西桂林 541004；2.广西无线宽带通信与信号处理重点实验室（桂林电子科技大学），广西桂林 541004）

（*通信作者电子邮箱walker_wyz@guet.edu.cn）

0 引言

2012 年3 月，国家密码管理局发布SM4 作为密码行业的标准。过去十年，专家学者们已经对SM4 密码算法的实现展开了一系列分析研究，特别是在侧信道分析（Side Channel Analysis,SCA)，如差分能量分析［1］、相关能量分析（Correlation Power Analysis,CPA)［2-3］等方面取得了若干重要进展。

侧信道分析通过分析密码算法实现过程中的中间值的信息泄露进行破译。时间［4］、功耗［5］、电磁波［6-7］等信息均可被用于分析密码系统。简单能量分析是侧通道分析中最经典的一种，即：不同的操作可能产生不同的功耗。通过观察采集到的设备加密过程中的能量波形，可以直接得到设备执行的具体操作，并进一步推测设备中的数据。1999 年，差分能量分析由Kocher 等［5，8］首先提出，后来由Messerges 等［9］将其形式化。差分能量分析仅利用1 位功率信息对能量迹进行分类［10］，是侧通道分析中使用最广泛的分析方法。为了改进原有的差分能量分析，Bevan 等［11］、Messerges 等［12］引入了多位差分功耗分析（Differential Power Analysis，DPA）。然后，基于汉明距离泄漏模型的相关能量分析在文献［13］中提出，该方案通过计算功率样本与密码算法中间值汉明距离之间的相关系数确定正确的密钥。该泄漏模型同样适用于以S 盒为单位的部分密钥；故当密钥空间较大时，可以通过分而治之的方法逐个恢复部分密钥，从而获得完整密钥。近几年，人工智能（Artificial Intelligence，AI）算法也开始应用于侧通道分析当中［14-15］。

注意到，为了追求效率，密码算法在硬件实现时通常采用并行实现的方案。此时，传统的基于单个S 盒的泄漏模型不再足够精确。文献［16］将传统相关能量分析中基于单个S 盒的泄漏模型改进为基于多个S 盒的泄漏模型，并通过引入遗传算法以对抗扩大的搜索空间。文献［17］在此基础上进行了改进，设计了基于多种群遗传算法的相关能量分析，以应对遗传算法过早收敛的问题。两者均大幅降低了恢复密钥所需的能量迹的条数，但都存在离线计算量较大、样本不足时得不到任何结果等问题。如何以尽可能小的计算量减少噪声，提高泄漏信息的利用率，成为研究的难点。

本文针对密码算法并行实现下相关能量分析效率低下的现象分析了原因，并提出了新的方法：阶梯式相关能量分析。其核心思想是优化传统相关能量分析的流程，提高能量迹的利用率，从而提高分析效率，减少能量迹的条数需求。阶梯式相关能量分析通过构造一种新的阶梯式方案并引入confidence 指标，可以在分析时回避正确性较低的分析结果，以确保每一次分析的结果有尽可能高的正确率。同时，随着阶梯式流程的推进，原本作为干扰项的部分噪声也将被逐一消除。整个分析过程变得越来越准确，这使得原本容易受噪声干扰的部分密钥的恢复过程变得不再容易出错。将阶梯式相关能量分析应用于SM4 密码算法的分析，本文得到了优于传统相关能量分析的结果。其计算量与传统相关能量分析相当，但明显减少了恢复完整轮密钥所需求的能量迹条数。

1 预备知识

1.1 SM4密码算法

SM4 密码算法与数据加密标准（Data Encryption Standard，DES）［18］及高级加密标准（Advanced Encryption Standard，AES）［19］类似，均为分组密码。SM4的分组长度和密钥长度均为128 比特，加密算法与密钥扩展算法均采用32 轮非线性迭代结构，以32 比特为单位进行加密运算。SM4 密码算法的加、解密算法的结构相同、使用的轮密钥相反，其解密轮密钥是加密轮密钥的逆序。

SM4密码算法的整体结构如图1所示。

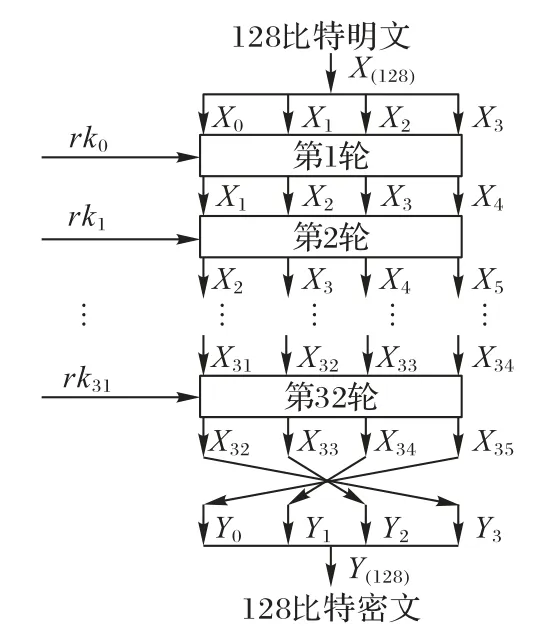
图1 SM4算法结构Fig.1 Structure of SM4 algorithm

明文输入为：

密文输出为：

第i轮运算输入为：

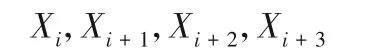
轮密钥为：

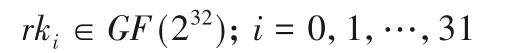
则轮函数定义为：

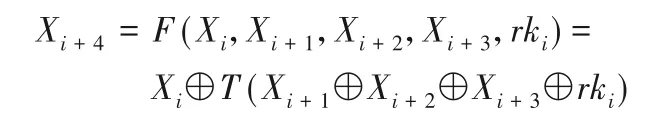
其中T为非线性变换和线性变换复合而成的合成置换。非线性变换由4个平行的S盒构成，S盒的数据均采用16进制。线性变换公式如下：

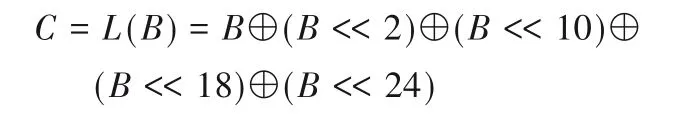
其中B为非线性变换得到的字。

最后一轮加密变换时，输出为：

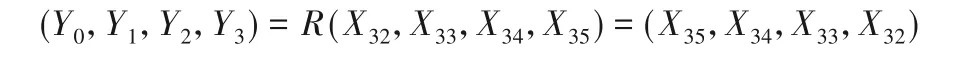
其中R为反序变换。

1.2 相关能量分析

文献［20］给出了相关能量分析的具体分析步骤，概括如下：

步骤1 选择中间值。选择合适的分析点是进行具体相关能量分析的前提。通过分析具体的密码算法，找到加解密过程中的一个中间值。这个中间值通常由一个函数f(p，k)生成，其中p是明文的一部分，k是与p相对应的密钥的一部分。满足这种条件的中间值可以泄露k。

步骤2 采集能量迹。搭建实验平台，进行d次加密或解密，每次采集长度为l的能量迹，构成大小为d×l的矩阵T。同时记录每次加密或解密时计算中间值f(p，k)所需的p，构成长度为d的向量P=(p1，p2，…，pd)。采集到的能量迹需要进行预处理（如对齐操作等），确保矩阵P中每一列数据对应的功耗均由相同的操作产生。

步骤3 计算假设中间值。对k进行穷举，记为向量K=(k1，k2，…，kn)，其中n表示k所能取到的所有值的数量。根据所有d次加密或解密对应的p和所有n个密钥假设，计算v=f(p，k)，构成大小为d×n的矩阵V。

步骤4 将中间值映射为功耗。选择合适的功耗模型，对V中的每个假设中间值计算对应的假设功耗值，得到由中间值矩阵V映射而成的功耗矩阵H，其大小依然为d×n。

步骤5 求相关系数。对矩阵H中的每一列hi与矩阵T中的每一列tj求相关系数，构成大小为n×l的矩阵R。其中的元素ri，j越大，表示hi与tj的匹配性越好。最大元素所对应的列标即为所求密钥。相关系数计算公式如下：

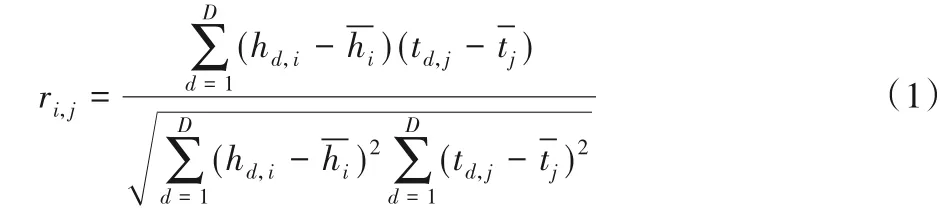
2 阶梯式相关能量分析

2.1 并行实现下的相关能量分析

在相关能量分析中，采集到的能量分为两部分：信息与噪声。信息，即分析对象对应的S 盒在运行时产生的能量；噪声，包括密码设备运行时其他模块产生的能量与白噪声。特别的，在密码算法并行实现的条件下，其他S 盒的能量信息也会包含在采集到的能量中。这些能量将被视为该次分析中的噪声，对分析结果产生干扰。

从图2中可以明确得知，单次分析的密钥比特数越多，噪声越小，但相应的搜索空间也会越大；反之，搜索空间减小，但受噪声的影响更大。如何权衡两者之间的关系，或者找到新的方法在同一数量级的计算量上提高分析的效率是研究的关键。传统相关能量分析采用分而治之的思想，每一次分析恢复一个S 盒对应的部分密钥，多次分析恢复完整轮密钥。但实际上在每一次部分密钥的恢复后，一些本可以被利用的信息被忽略掉了。

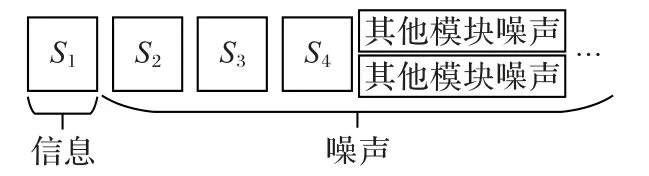
图2 采集能量的构成Fig.2 Composition of collected power

2.2 阶梯式方案

相关能量分析的传统方案通过分而治之的思想，利用多次分析分别恢复每个S 盒对应的部分密钥，如图3 所示：第一次分析第一个S盒对应的部分密钥，之后每次分析下一个S盒对应的部分密钥，直到分析完所有S 盒对应的部分密钥，构成完整轮密钥。图3中m表示完整轮密钥包含的数据字的个数。每一次分析的过程是相互独立的，即一次分析的结果不会对其他分析造成任何影响。当噪声较大或能量迹条数过少时，分析的成功率降低。而任意一次分析的失败都将导致完整密钥恢复的失败，这是相关能量分析失败最常见的原因。

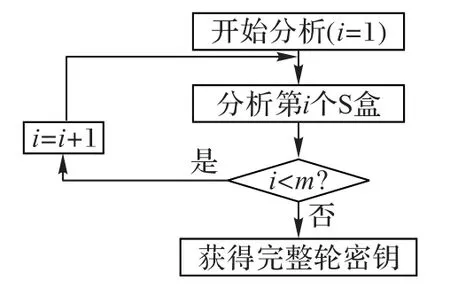
图3 传统相关能量分析方案Fig.3 Classic CPA scheme

然而，成功完成其中任意一次分析后，所获的部分密钥对下一次分析而言并不是没有任何意义的。将一次分析的结果纳入下一次的分析目标，将在维持搜索空间不变的前提下，有效减少噪声、增加信息。如：第一次分析以第一个字节的密钥为分析目标，得到分析结果：k1=01010101。第二次分析，将第一字节与第二字节同时作为分析目标。其中第一字节固定为k1=01010101 不变，第二字节k2从00000000 遍历至11111111。每次分析的密钥字节数越来越长，由图2 可知噪声将会减少。但是因为每次分析只添加一个字节的新密钥，其他密钥都是已知的、固定不变的，所以搜索空间依然是28=256。具体方案为：第一次分析第一个S盒对应的8比特密钥，之后每次分析都将下一个S 盒对应的8 比特密钥纳入攻击范围。在保持前一次分析结果不变的前提下，遍历下一个S 盒对应的8比特密钥，直到最后一次分析，获得完整的轮密钥。

阶梯式方案的优势在于：随着阶梯式流程的推进，分析的密钥字节数越来越长，噪声越来越少。这意味着后分析的部分密钥将有越来越高的正确率。但相关能量分析的成功，即完整密钥的恢复，取决于每一次对部分密钥分析的成功与否，而非单次分析成功率的最大值。前几次分析的正确性成了阶梯式方案的短板。单纯的阶梯式方案并不能对前几次分析的成功率产生有效影响，而后几次分析成功率的提升对完整密钥恢复的成功率提升非常有限，所以需要进一步引入文献［21］中提及的confidence指标（下文中简称c指标）：

其中：r1为一次相关能量分析中获得的最大的相关系数；r2为同一次相关能量分析中获得的第二大的相关系数。c 指标为两者之差，它可以有效地衡量这一次相关能量分析结果的正确性。指标数值越大，结果为正确的可能性越大，反之则越有可能是受噪声干扰所得的错误结果。

具体分析流程如图4。描述如下：第一次分析，依次对4个S 盒对应的部分密钥进行分析，并计算每次分析的c 指标。保留c 指标最高的一次分析所得的密钥。第二次分析，将已恢复的密钥纳入分析目标，继续分析其余3个S盒对应的部分密钥，并计算每次分析的c 指标。如：第一次分析已恢复k3，则依次分析k1|k3，k2|k3，k4|k3，其中k3固定为已恢复的值，k1，k2，k4依次遍历256种候选值。保留c指标最高的一次分析所得的密钥。以此类推，直到第四次分析结束，恢复出完整轮密钥。为了便于理解具体流程，表1 给出了阶梯式相关能量分析实例中每一次分析的具体参数。

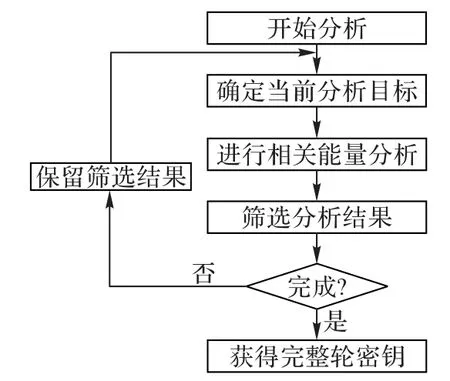
图4 阶梯式相关能量分析方案Fig.4 Stepwise CPA scheme

表1 阶梯式相关能量分析实例Tab.1 Example of stepwise CPA

c 指标的引入在一定程度上解决了前几次分析正确率得不到保证的问题。可以说，依据c 指标筛选分析结果是在资源已定的情况下被动地提升成分析的功率，而阶梯式方案的推进则是主动消除噪声的影响，提升成功率。两者的结合有效提高了相关能量分析的成功率，尤其是在噪声较大、能量迹条数较少的情况下。

传统相关能量分析的基本思想是“分而治之”，但在分治的过程中，任何一次分析的错误都将导致最终完整轮密钥恢复的失败。本文提出的阶梯式相关能量分析，其基本思想是“步步为营”。相较于传统相关能量分析，只要有一次分析成功，就可以继续分析下去。而且随着阶梯式流程的推进，一些本可能发生错误的分析也将在接下来的分析中因噪声的减少而被进一步修正。

2.3 阶梯式相关能量分析的构造

阶梯式相关能量分析包含以下主要步骤：确定分析目标、相关能量分析、筛选分析结果、状态更新。

3 实验与结果分析

3.1 模拟实验

在模拟实验中，在C 语言仿真平台上对SM4 算法的S 盒操作进行了模拟，并分别添加两种不同程度的噪声，其标准差分别为σ=3.0 和σ=5.0。在这两组数据上分别执行了传统相关能量分析和本文提出的阶梯式相关能量分析。实验按照不同的给定能量迹条数分组进行，从100 到1 000，间隔为10，每组实验取1 000 次实验结果的平均值。图5 给出了这两种方案的成功率。表2总结了在成功率达到50%和90%的前提下，两种方案对能量迹条数的需求和相应的计算量。由于计算量主要取决于相关系数的计算次数，所以这里忽略了排序操作的计算量，只记录恢复完整轮密钥所需计算相关系数的次数。

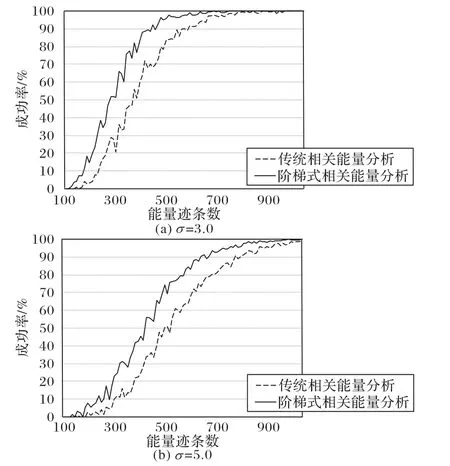
图5 不同噪声下能量迹条数与成功率的关系Fig.5 Relationship between the number of power traces and success rate under different noises

表2 阶梯式相关能量分析与传统相关能量分析对比Tab.2 Comparison of stepwise CPA and classic CPA

实验结果表明，在能量迹条数相同的前提下，本文提出的阶梯式相关能量分析的成功率明显优于传统相关能量分析。当σ=3.0时，阶梯式相关能量分析只需要420 条能量迹就可以达到90%的成功率，而传统相关能量分析需要560条，减少了25%的能量迹条数需求。当σ=5.0时，阶梯式相关能量分析只需要630 条能量迹就可以达到90%的成功率，而传统相关能量分析需要760 条，减少了17%的能量迹条数需求。值得一提的是，阶梯式相关能量分析的计算量为2 560 次，是传统相关能量分析的2.5 倍。相较于计算量达到几万甚至几十万的基于遗传算法的相关能量分析（Correlation Power Analysis based on Simple Genetic Algorithm，SGA-CPA）［16］和基于多种群遗传算法的相关能量分析（Correlation Power Analysis based on genetic algorithm and Multiple Sieve method，MS-CPA）［17］，阶梯式相关能量分析的计算量非常小，可以认为是与传统相关能量分析的计算量处于同一数量级上。

3.2 FPGA上的实验

在实际实验中，使用SAKURA-G 自主搭建实验平台。SAKURA-G是一款专门为硬件安全方面的研究和开发而设计的FPGA 板。它由两块Spartan-6 FPGA 集成而来：主FPGA 用于密码算法的实现；控制FPGA 用于相应控制逻辑的实现。超低噪声的设计使能量分析变得更加容易。

在具体的相关能量分析实验中，把SM4 硬件电路下载到SAKURA-G 开发板上，然后将其触发输出和信号输出分别与示波器相连，并将主控制口通过USB 连接线与电脑相连。对固定的密钥和已知的随机明文执行SM4 密码算法，并通过使用LeCroy WaveRunner 610Zi 示波器与旁路分析软件SCAnalyzer 完成5 000 条能量迹的采集。实际采集到的每一条能量迹为一个长度为30 000 的数组，记录了电压随时间变化的曲线。为了降低噪声和减少计算量，需要对能量迹进行重采样，即数组中的每10个点取平均数，记为一个点。

首先，对这5 000 条能量迹进行传统相关能量分析，计算单字节部分密钥的所有可能值对应的中间值与能量迹的相关系数。图6 给出了实验结果：虚线表示正确密钥，不同灰度的实线表示其他错误密钥。用于计算相关系数的能量迹条数为10～5 000，间隔为10。当能量迹条数大于3 430 条时，正确密钥对应的相关系数始终大于错误密钥对应的相关系数，这意味着本次实验中使用传统相关能量分析恢复密钥至少需要3 430条能量迹。

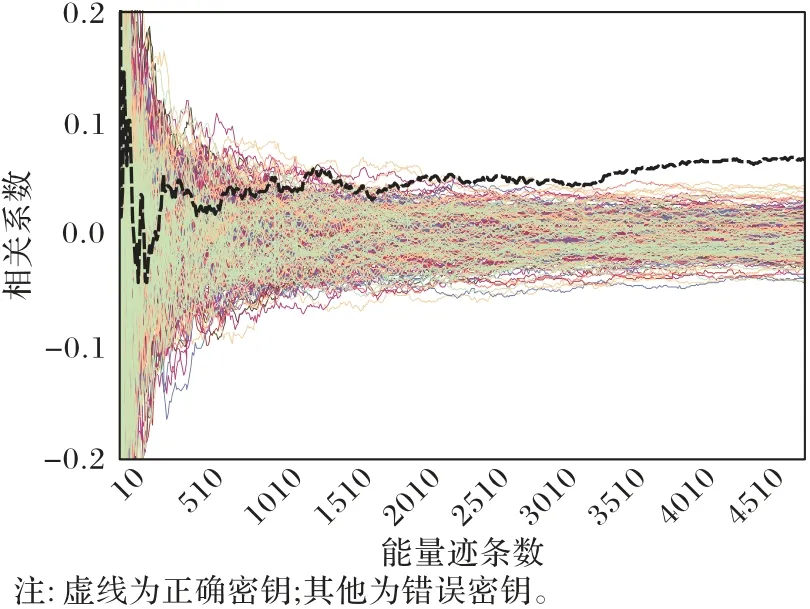
图6 相关系数与能量迹条数的关系（传统相关能量分析）Fig.6 Relationship between the number of power traces and correlation coefficient（classic CPA）

其次，对同样的5 000条能量迹计算其与完整密钥对应的中间值的相关系数，旨在找出同等实验环境下通过相关能量分析恢复完整轮密钥所需能量迹的最小数量。由于完整轮密钥长度为32 比特，穷尽所有可能的计算量较大且没有必要，所以只选择部分最具“竞争力”的错误密钥与正确密钥进行对比。文献［17］已给出相关结论，即候选密钥中正确的字节数越多，其对应的相关系数越大。故本次实验中只选择28×4个只含有3 个正确字节的候选密钥与正确密钥做对比。经过实验结果的分析与对比发现，在本实验中，当第2 个S 盒对应的部分密钥错误、其他部分密钥正确时，错误密钥对应的相关系数与正确密钥对应的相关系数最接近。所以为了精简图表数据，图7 将只给出这部分实验结果的数据：其中虚线表示正确密钥，不同灰度的实线表示其他错误密钥。用于计算相关系数的能量迹条数为10～5 000，间隔为10。当能量迹条数大于3 100条时，正确密钥对应的相关系数始终大于错误密钥对应的相关系数，这意味着本次实验中以相关能量分析为基本思想恢复完整密钥最少需要3 100 条能量迹。当然这是建立在将相关能量分析的搜索空间扩大到232的前提下的。这是通过巨大计算量换取分析精度的一种方式。

最后，同样是这5 000 条能量迹，对其进行阶梯式相关能量分析，记录每一次分析的结果对应的相关系数，并与正确密钥对应的相关系数进行对比。图8 给出了实验结果：其中虚线表示正确密钥，4种灰度的实线由浅至深分别表示4次分析的结果。用于计算相关系数的能量迹条数为10～5 000，间隔为10。当能量迹条数达到2 370条时，最后一次分析的结果对应的相关系数已基本与正确密钥对应的相关系数重合。当能量迹条数大于3 100条时，两者完全重合。这说明阶梯式相关能量分析恢复正确密钥的能力已经非常接近将搜索空间扩展到最大时的极限。

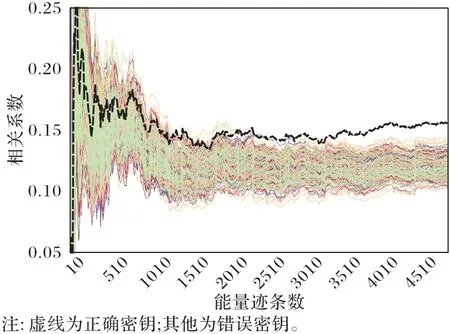
图7 相关系数与能量迹条数的关系（完整轮密钥）Fig.7 Relationship between the number of power traces and the correlation coefficient（whole round key）

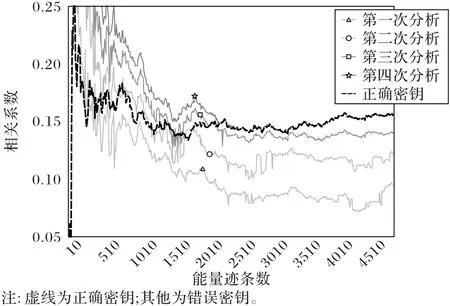
图8 相关系数与能量迹条数的关系（阶梯式相关能量分析）Fig.8 Relationship between the number of power traces and correlation coefficient（stepwise CPA）

本次实验中，使用传统相关能量分析恢复密钥至少需要3 430 条能量迹，而将搜索空间扩大到232时，对能量迹条数需求的极限是3 100 条。阶梯式相关能量分析的结果在能量迹条数达到2 370 条时基本与正确密钥吻合，在达到3 100 条时完全吻合。不同实验中的数据存在细微的差别，但数据间的关系和比例大致不变。由此可以看出阶梯式相关能量分析相对于传统相关能量分析有明显的优越性。

4 结语

本文讨论了相关能量分析在并行实现下分析效率低下的原因，提出了阶梯式方案，并通过引入confidence 指标，基于SM4 密码算法的结构，构造了阶梯式相关能量分析。实验结果表明阶梯式相关能量分析以较小的计算量有效降低了传统相关能量分析对能量迹条数的需求，是一种精确、快捷的分析方案。接下来进一步的研究可以考虑对能量迹进行分析和筛选，以减少计算量、提高分析效率。