立方多变量公钥密码体制的最小秩分析

张 栖，聂旭云

（1.电子科技大学信息与软件工程学院，成都 610054；2.网络与数据安全四川省重点实验室（电子科技大学），成都 610054）

（*通信作者电子邮箱1106845293@qq.com）

0 引言

自1988 年Matsumoto 和Imai 首次提出具有里程碑意义的MI（Matsumoto Imai）多变量公钥密码体制（Multivariate Public Key Cryptosystem，MPKC）［1］以来，该密码学原语的设计与安全性分析逐渐成为密码学界与信息安全界的一个研究热点。

多变量公钥密码体制的安全性基于求解有限域上随机产生的多变量二次多项式方程组（Multivariate Quadratic，MQ）的问题，它是一个NP-困难问题。MQ 问题也可扩展为求解有限域上随机产生的多变量三次多项式方程组（Multivariate Cubic，MC）的问题。多变量公钥密码体制一般由两个仿射变换和一个中心映射复合而成，其中复合函数的表达式为公钥，两个仿射变换为私钥。多变量公钥密码体制的构造关键在于它的中心映射的构造，而针对多变量公钥密码的安全性分析也集中在分析其中心映射。关于多变量公钥密码体制的更多详细描述可参考文献［2］。

最小秩问题（MinRank Problem，MR Problem）指的是给定正整数m、n、r、j及j个矩阵M0，M1，…，Mj-1∈Mm×n(K)，确定是否存在一组系数λ1，λ2，…，λj-1∈K，使得

这是一个NP-困难问题。

每一个多变量二次多项式中的齐二次项可用一个对称矩阵来表示。公钥多项式对应的矩阵能够表示成为中心映射多项式对应的矩阵的线性组合。一旦中心矩阵多项式对应的矩阵的秩较小，就可以采用最小秩攻击（MinRank Attack，MR Attack）来尝试恢复私钥。事实上，最小秩攻击，就是利用在公钥多项式对应的矩阵的线性组合中寻找具有最小秩矩阵来还原其私钥-线性仿射变换U。

这一类攻击最早是由Kipnis 等［3］提出用于分析隐藏域方程（Hidden Field Equations，HFE）加密体制的安全性。2013年，Bettale 等［4］改进了Kipnis等的攻击方法破解了multi-HFE。Zhang等［5］利用秩攻击破解了Yasuda等提出的一个签名方案，并提出了一种改进方案来抵挡秩攻击［6］。秩攻击同样可用于分析不平衡油醋类（Unbalanced Oil and Vinegar，UOV）签名体制［7］。在秩攻击的要求下，该类体制一般要求醋变量的个数是油变量个数的两倍。Yasuda 等［8］基于彩虹体制（Rainbow）提出了一种改进的数字签名方案，但很快就被Perlner 等［9］用最小秩攻击所破解了，Ikematsu 等［10］借鉴了该体制的思想，提出一种基于HFE 体制的加密方案来抵抗最小秩攻击。另外，秩攻击还可以在其他密码学领域作为安全性分析方法，如认证方案（Authentication Scheme）［11］。

Square 加密方案［12］与MI 体制和HFE 体制一样，是属于“小域-大域”方案，即其公钥是有限域K上的多变量二次多项式，而其中心映射是K的扩域上的单变量平方运算。相对于HFE 体制而言，Square体制极大地缩减了加密和解密成本，但同时该体制既存在差分对称性［13］，也具有最小秩缺陷。立方加密方案［14］是Square方案的改进。通过将中心映射改为扩域上的单变量立方运算，使得公钥多项式的次数由二次提升到三次，来抵抗针对具有低秩中心映射的二次多变量公钥密码体制的最小秩攻击。本文分析表明，立方加密方案的中心映射经过差分过后，具有和Square 方案的一样的低秩缺陷。因此，立方加密方案的公钥差分后得到的系数矩阵，也具有低秩线性组合。结合改进的Kipnis-Shamir 方法［4］，即可恢复该体制的私钥。

1 预备知识

1.1 多变量公钥密码体制的一般形式

令k=Fq是一个q元域，n和m是两个正整数。U和T分别是kn和km上的两个随机选取的仿射变换，F：kn→km称为中心映射。x=(x1，x2，…，xn)为明文变量，y=(y1，y2，…，ym)为密文变量。令

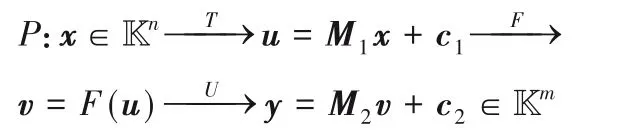
函数P=U∘F∘T的表达式为多变量公钥密码体制的公钥，通常为一组多变量二次多项式。U和T为私钥。

注意，若在大域上构造中心映射F，需引入k-线性同构φ：K→kn。其中K为k的n次扩域，F为K上的单变量多项式。公钥形式如下：

1.2 最小秩攻击

最小秩攻击是一个NP-困难问题。在r比较小的时候，问题可解。

Kipnis 等［3］首先使用最小秩攻击来分析HFE 公钥密码体制，其方法被称为Kipnis-Shamir方法。

观察P=U∘φ∘F∘φ-1∘T，P是已知的公钥，U、T和f是未知的私钥。在文献［3］中，作者提出可以通过k-线性同构φ将公钥P提升到大域上得到P*，方法如下：

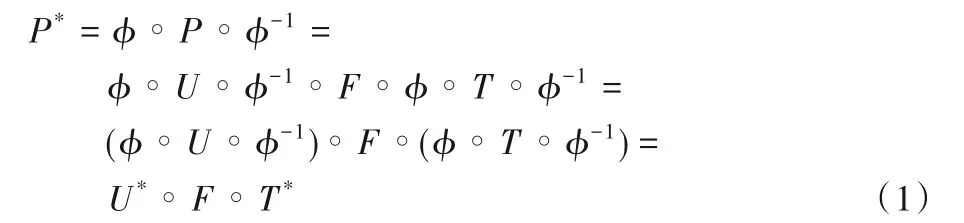
公式两边同时复合U*-1，可得到U*-1∘P*=F∘T*，由这个方程，最终可以得到“基本方程”，如下：

其中：P*k表示矩阵P*的每个元素经过qk幂次提升，uk(k=0，1，…，n-1)表示矩阵U的第一列元素。如果矩阵F的秩r是有界的，那么P'的秩也是有界的。当秩r足够小时，恢复uk就可以规约到求解最小秩问题。

如何求解最小秩问题，Kipnis 和Shamir 提出了Kipnis-Shamir模型［3］。对于一个秩为r的线性组合，它一定存在n-r维的左核，可以根据已知的k个齐次公钥矩阵和确定的秩r，得到一个由r(n-r)+k个变量n(n-r)个方程组成的多项式系统。

注意，Kipnis-Shamir 方法需要使用k-线性同构将公钥矩阵从小域提升到大域，这导致后续最小秩问题求解的成本增加。Bettale 等［4］基于Kipnis-Shamir 方法提出了一种改进方法，不需要将公钥从小域提升到大域，可以直接求解最小秩问题，极大地提升了最小秩问题的求解速度。本文实验部分也是采用这种方法。

1.3 Square加密方案

Square 加密方案［12］是Baena 等根据HFE 方案的设计思想设计而成。令k为特征值为q的有限域，K是k的n次扩域。φ：K→kn是标准k-线性同构，φ-1为它的逆。Square体制的中心映射为：F：Y=X2。为了保证该映射可逆，需满足gcd(2，qn-1)=1。

和多变量公钥密码体制的一般形式一样，它的公钥P=U∘f∘T=U∘φ∘F∘φ-1∘T，私钥为U，T和F。对明文变量加密是通过求解P(x)=y完成，解密是通过对三个映射U、T和F的求逆完成。

根据它的中心映射的形式，可确定其对应系数矩阵的秩为1。也就是说，该体制的公钥在经过同构变换从小域映射到大域后，所对应的系数矩阵存在在一组秩为1 的线性组合，形式如下：

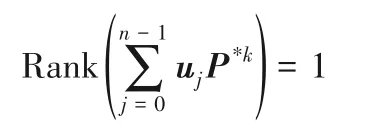
使用Kipnis-Shamir 模型，求解即可得到uk。完整的私钥恢复过程可参考文献［3］。

1.4 立方加密方案

立方加密方案是根据Square 加密方案改进而成，该方案的中心映射为：F：Y=X3。为了保证该映射可逆，需满足gcd(3，qn-1)=1，这就要求q≡2(mod 3)且q为奇数。设d为满 足3t≡1(mod(qn-1)) 的整数，则F-1为X=F-1(Y)=。

相较于Square 加密方案，该方案中心映射的次数由2 增加到3，它的公钥矩阵也由二维矩阵扩展到三维矩阵。尽管最小秩问题可以由二维矩阵扩展到三维矩阵，但如何确定一个三维矩阵的秩是非常困难的，甚至很难知道一个三维矩阵可能有的最大秩［15］。

2 立方加密方案的最小秩分析

虽然立方加密方案可以抵抗针对二维矩阵的最小秩攻击，但经过分析，可发现该体制的中心映射差分过后具有和Square方案中心映射相似的性质，在A点的差分结果如下：

差分过后齐二次项对应矩阵和Square方案中心映射对应矩阵的秩相等，并且立方加密方案的公钥经过差分后，逆向推导的中心映射F'的性质和DF(X，A)相似，关系如下：

其中a∈kn，F'是秩为1 的二次多项式，DP(x，a)表示公钥多项式P1，P2，…，Pn在a点的差分。对于这种低秩中心映射，可以使用最小秩攻击恢复其私钥。同时，为了降低计算成本，本文采用一种扩展的Kipnis-Shamir 方法［4］。这种方法通过将k-线性同构φ及它的逆φ-1表示成矩阵形式，不需引入另外的φ，可直接在小域上求解最小秩问题。

2.1 改进的Kipnis-Shamir方法

命题1［4］设(θ1，θ2，…，θn)∈Kn为域K基于域k上的一组基，Mn∈Kn×n是一个由这组基经过Frobenius 变换得到的矩阵，形式如下：

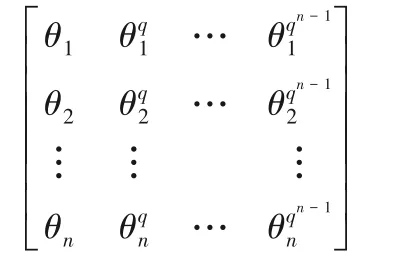
k-线性同构φ：K→kn可以表示成如下形式：

它的逆φ-1可表示成：

(v1，v2，…，vn)⋅Mn[1]表示该向量第一个元素。

命 题2［4］设矩阵A=[ai，j]∈kn×n，矩 阵B=[bi，j]=A⋅Mn∈Kn×n，则矩阵B的各列存在如下关系：

在得到Mn后，即可使用矩阵乘积来表示复合映射DP(x，a)=U∘φ∘F'∘φ-1∘T。首先取多项式组DP(x，a)的齐二次项系数矩阵，得到G1，G2，…，Gn。令h1，h2，…，hn=φ-1∘F'∘φ表示基域多项式组，它们的系数矩阵为H1，H2，…，Hn。根据式（4）和（5），可以用矩阵Mn来表示这组系数矩阵，形式如下：

其中：F*k表示中心映射F'的qk次幂的系数矩阵，它的元素表示为。复合映射的矩阵表示过程如下：

将式（6）代入，得：

令(s0，0，s1，0，…，sn-1，0)为矩阵S的第一列元素，则根据式（8），可得到“基本方程”，如下：

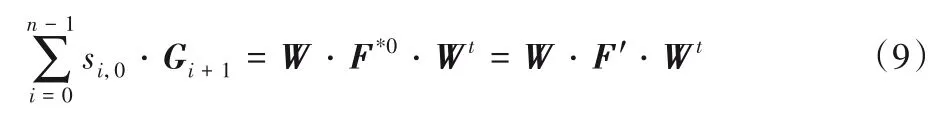
由前文分析可知，矩阵F'的秩r为1，则恢复si，0(0 ≤i≤n-1)可以规约到最小秩问题的求解。

2.2 实验步骤及结果

完整的实验过程可在普通PC上用MAGMA实现，PC的配置为：Inter Core i5-4300U CPU，2.50 GHz，8 GB 内存。给定q，n，秩r=1，具体实验步骤如下：

步骤1 对于给定公钥P1，P2…，Pn，依次求解出差分，得到差分过后二次项所对应系数矩阵G1，G2，…，Gn。

步骤2 生成一个(n-r) ×n的矩阵KM，形式如下：

矩阵行向量是线性无关的。根据式（7），存在非零向量(s0，0，s1，0，…，sn-1，0)，使 得。求解得到(s0，0，s1，0，…，sn-1，0)，根据命题2，即可恢复完整的矩阵S：

步骤3 在恢复U后，令(w0，0，w1，0，…，wn-1，0)为矩阵W的第一列元素，矩阵K为的左核，可得到如下方程组：

其中l=1，2，…，r，Frobi(K)表示K的每列元素经过Frobenius变换［4］后得到的矩阵。求解出这个方程组后，根据命题2，即可恢复W：

步骤4 公钥已知，在成功恢复矩阵MU和MT后，根据P=U∘φ∘F∘φ-1∘T，逆向恢复中心映射F。

文献［14］中的推荐参数为n=15，q=59，r=1。根据文献［16］，该攻击的计算复杂度主要由最小秩问题求解决定，为：

由于域的大小并不会影响理论分析的结果，因此，在实验中，令q=5，n的大小不超过30。实验运行时间和复杂度估计如表1 所示。从表1中可以看出，攻击的效率较高，符合理论分析的结果。

表1 不同参数下最小秩攻击的代价和破解时间的比较Tab.1 Comparison of cost and cracking time of MinRank attack under different parameters

为了能够让该体制抵抗最小秩攻击，同时考虑到效率问题，本文建议使用减方法来提高该体制的安全性，减去的公钥多项式个数为s=2。

2.3 实例

为了更清楚阐述攻击流程，在本节展示一个具体实例。同时为了简化计算流程，本实例采用可逆线性变换而不是仿射变换。令q=5，n=7，线性变换U和T的系数矩阵MU、MT分别为：

恢复得到的U，T，F即为一组等价密钥。

3 结语

本文结合差分方法和最小秩攻击方法，对立方多变量公钥加密体制进行了安全性分析，发现该体制中心映射经过差分后具有低秩缺陷，利用本文的攻击方法可成功地恢复体制的私钥。对立方多变量公钥加密体制使用减方法增强后可得到立方多变量公钥签名体制。减方法在减去一定个数的公钥多项式后，剩余的公钥多项式差分后所对应的系数矩阵不能构成差分后中心映射对应矩阵的线性组合，使得最小秩攻击无法对其产生作用。未来的工作中，将进一步分析该签名体制的安全性。