面向全局优化的时空众包任务分配算法

聂茜婵，张 阳，余敦辉，2*，张兴盛

（1.湖北大学计算机与信息工程学院，武汉 430062；2.湖北省教育信息化工程技术研究中心（湖北大学），武汉 430062）

（*通信作者电子邮箱yumhy@hubu.edu.cn）

0 引言

随着Web2.0 技术的兴起，大量在线Web 应用催生了众包［1-3］这种通过群体智慧求解问题的新兴商业生产模式。众包是指“一种把过去由专职员工执行的工作任务通过公开的Web 平台，以自愿的形式外包给非特定的解决方案提供者群体来完成的分布式问题求解模式”［4］。而随着智能移动设备的普及和共享经济模式的迅猛发展，赋予了众包任务更多的时空属性，衍生出一种全新的众包类型——时空众包［5-7］。时空众包是指在时空约束的条件下，将具有时空特性的众包任务分配给非特定的众包工人群体，并要求众包工人以主动或被动的方式来完成众包任务。近年来，全国流行的各类实时专车类服务平台，例如滴滴出行、Uber 等，均采用时空众包方式提供服务。而在很多线上到线下（Online-to-Offline，O2O）应用、灾情监控和物流管理等领域，也将时空众包技术运用其中以提高其服务质量。然而，现有的研究大多局限从众包平台或工人的单一角度出发进行优化，且没有满足实际应用中连续分配任务的需求。因此，本文提出一种基于预测分析的全局优化在线任务分配算法（Global Optimization online Mission Assignment algorithm based on predictive analysis，GOMA），该算法基于在线随机森林和门控循环单元网络预测出下一时间戳内众包对象（众包任务和工人）的分布情况，进而结合当前时间戳内众包对象的情况构造二分图模型，最后采用带权二分图最优匹配算法完成任务分配，从而实现众包平台、众包任务、众包工人三方综合效益的全局优化。

本文主要工作在于：

1）提出一种综合考虑众包平台、众包任务、众包工人三方效益的在线任务分配算法思想，进行多目标优化，更加切合实际应用中的需要。

2）在任务分配中，考虑众包工人动态移动的特性，对任务进行连续动态分配。

1 相关研究

任务分配［8-10］作为时空众包领域研究的核心问题之一［11］，众多学者对其展开了深入的讨论。

文献［12］在随机阈值算法的基础上，提出了面向三类众包对象的自适应阈值算法，验证了算法在提高分配效用方面的有效性；文献［13］以贪心算法作为基线算法，提出了一种基于两阶段框架模型的全球微任务分配算法，在确保算法执行效率的同时提高任务分配的效用；文献［14］以最大化任务的成功分配数为优化目标，提出了一种基于多臂赌博机的在线任务分配算法，为优化任务分配效用提供了新思路；文献［15］在众包工人查询算法的基础上，提出了一种基于动态效用的阈值选择算法，通过动态效用对比以提升分配效用；文献［16］提出一种基于众包对象预测的在线任务分配算法，在现有众包对象的基础上，采用线性回归模型预测动态出现的众包对象，进行任务分配，实现任务分配效用的全局优化。这类方法仅局限于众包平台的角度，以任务分配总效用最大化为目标进行优化，而未考虑众包工人的差旅成本以及众包任务的等待时间。

文献［17］在贪心算法的基础上，提出时间空间预测器对众包任务进行预测，进而辅助任务分配，旨在最小化一段时间内工人的总体差旅成本；文献［18］针对最小化最大匹配距离的问题，提出了一种交换链算法，有效地解决了最差匹配情况下的匹配距离最小化的问题；文献［19］面向最小化匹配距离的问题，进行综合性对比实验，证明了贪心算法解决该类问题的有效性。这类方法仅局限于众包工人的角度，以工人平均差旅成本最小化为目标进行优化，而忽略了众包任务等待时间以及任务分配的总效用，同时也没有考虑众包平台、任务发布者的利益最大化。

文献［20-21］从众包平台和工人的角度出发，文献［20］根据众包工人的密度进行众包任务的范围调节，提出一种基于统计概率进行预测分析的方法，能够在提高任务分配总效用的同时降低工人的差旅成本；文献［21］基于分而治之的思想，提出了一种基于二分法框架模型的在线任务分配算法，力求最大化任务分配数量以提高分配效用，同时最小化工人的差旅成本；文献［22］从众包平台和众包任务的角度出发，综合考虑任务分配总效用和任务等待时间，提出一种基于分配时间因子的动态阈值算法，提升分配总效用的同时降低任务的平均等待时间。这类方法从众包平台、工人、任务中某两方的角度出发进行双目标优化，但没有从众包平台、任务和工人三方角度出发，综合考虑三方效益，所以仍然存在改进空间。

综上，不难看出现有研究中存在以下几点不足：

1）现有研究大多以单目标优化为主，从众包平台或工人单一角度出发，聚焦于提升任务分配总效用或降低工人的差旅成本，而少量研究从双方角度出发，进行双目标优化。对于从众包平台、任务和工人三方角度出发，综合考虑三方效益的任务分配算法研究尚未出现。而考虑不完善的任务分配算法无法满足实际应用中的需要。

2）大多在线任务分配算法仅依据当前时间戳内已有众包对象进行任务分配，对当前时间戳内的任务分配进行局部优化，而在实际应用中，任务分配是连续动态进行的，现有大多任务分配方案无法满足连续分配中全局优化的目标。而已有基于预测方法进行任务分配的算法，尚未考虑众包工人动态移动的特性，无法满足实际应用环境的需要。

本文以实时专车类时空众包应用作为背景，针对上述问题，从众包平台、众包任务、众包工人三方的角度出发，以提高众包任务分配三方的综合效益指标作为优化目标，针对连续任务分配问题，提出了一种采用随机森林和门控制循环单元（Gated Recurrent Unit，GRU）网络进行预测分析的全局优化在线任务分配算法，在当前时间戳内众包对象分布情况的基础上，结合下一时间戳内众包对象的预测情况进行任务分配，实现连续任务分配过程中众包任务分配三方综合效益全局优化的目标。

2 问题定义

定义1众包任务m。m由任务请求者在众包平台上发布，通常被定义为如下四元组的形式。其中：lm是任务m在二维坐标系中所处的位置，任务m的发布时间是pm，任务m的截止时间是dm，gm表示完成该任务m的工人所获得的报酬。

定义2众包工人w。w是m的完成者，通常被定义为如下六元组的形式。其中lw是工人w在二维坐标系中所处的位置；rw是工人w的范围半径，工人w的接单范围Rangw表示工人w愿意接受的任务的范围，即以lw为圆心，rw为半径的区域；dirw表示工人的移动方向dirw={N，S，W，E}；工人w在平台上线时间是pw，工人w在平台下线的时间是dw；sw表示工人在平台上所完成的历史任务的成功率。对于众包工人，开始执行一个众包任务视为工人从平台下线；执行完一个众包任务后，若继续接单则视为工人在众包平台重新上线。为简化计算，本文定义工人的行驶速度均为speed，工人单位路程所花费的成本为per。

定义3任务工人匹配对mp。mp定义为，表示众包任务m和工人w的组合。

定义4分配效用Up。Up表示将众包任务m分配给众包工人w后所产生的效用，即匹配对的效用，定义为任务回报值gm与工人成功率sw的乘积，即：

其中：gm∈(0，1)，sw∈(0，1)，故Up∈(0，1)。

定义5任务等待分配时间ATm。ATm表示众包任务m在平台发布后，等待分配的时间，用于衡量任务的等待分配程度，等待程度高的任务优先分配。ATm即为任务发布时刻Pm到任务分配时刻Ta的时间差：

定义6任务差旅时间MTm。MTm表示任务工人分配后，工人到达任务地点的时间，即为任务分配时刻到工人到达时刻的时间差。当工人速度一定时，任务与工人距离小的优先分配。则MTm表示如下：

其中：MDmw表示任务和工人间的曼哈顿距离。

定义7工人机会成本COw。工人的机会成本COw表示工人w在平台上线后处于空闲状态到工人被分配处于工作状态所花费的成本，当前已花费机会成本高的工人优先分配。COw表示为：

其中Lf表示工人处于空闲状态所行驶的总距离，即工人从平台上线到下线时间内所行驶的距离（曼哈顿距离）：

定义8任务工人匹配对综合效益CB（Comprehensive Benefits）。mp具有分配效用Up、任务等待分配时间ATm、任务差旅时间MTm、工人机会成本COw四项属性，从众包三方角度考虑，定义综合效益指标CB用于综合衡量Up、ATm、MTm、COw四项指标：

其中：权重系数α、β、γ、η根据熵权法确定，AT'm、MT'm和CO'w是离差法标准化处理后的取值。标准化处理方法如下：

其中：xi为该指标当前样本的原值，max(Xi)为该指标的最大值，min(Xi)为该指标的最小值，x'i为该指标当前样本处理后的取值。

定义9综合效益最大化的众包在线任务分配问题Crowdsourcing online Mission Assignment to Maximize the Comprehensive Benefits，CMA-MCB）。在时空众包环境下，给定众包任务集合M、众包工人集合W和任务工人匹配对综合效益CB的计算函数，寻求一个任务分配的结果集R使得三方综合效益最大化，即最大化任务工人匹配对综合效益CB：

分配结果集R由匹配对mp组成，其中每个匹配对mp需满足以下基本约束：

时间约束 只有众包任务m和众包工人w同时平台在线时，才能实现分配，且众包任务m必须在任务的截止时间dm前分配，否则无法完成分配。

不变性约束 众包任务一旦完成分配，分配结果则不能改变。

空间约束 众包任务m的空间位置lm必须在分配的众包工人w的接单范围内，即|lm-lw|＜rw。

3 GOMA

针对提出的CMA-MCB 问题，首先将一个任务分配周期划分为n个固定时间长短的时间戳，在每个时间戳内进行任务分配。每轮分配首先设置当前待分配工人的接单范围，进而执行基于预测分析的全局优化在线任务分配算法（GOMA），引入下一时间戳内众包对象的分布情况作为当前分配的依据，基于在线随机森林和GRU 两种预测模型，预测出下一时间戳内众包对象分布，结合当前时间戳内众包对象的分布情况，执行带权二分图最优匹配算法（KM 算法），完成本轮任务分配。

GOMA主要可分为以下三步：

1）执行基于在线随机森林的众包对象动态预测算法（Dynamic Prediction algorithm for crowdsourcing objects based on online Random Forest，DPRF）和基于在线随机森林回归预测模型，预测下一时间戳内众包对象动态出现的情况。

2）执行基于GRU 的工人移动轨迹预测算法（Worker Movement Trajectory Prediction algorithm based GRU，WMTP）和基于GRU 循环神经网络预测出当前已有众包工人在下一时间戳时的空间分布。

3）在当前时间戳的众包对象分布的基础上，结合1）、2）预测的众包对象的分布情况，执行带权二分图最优匹配算法，完成任务分配。

3.1 DPRF

对于下一时间戳内新出现众包对象的预测，DPRF将时空众包地理场景拟合成n×n的网格图，基于分而治之的思想，分别对网格图中每一个小室cell进行预测。每个小室cell预测可分为众包对象的空间分布预测和众包对象的属性参数预测。

对于空间分布预测，DPRF首先预测每个小室内众包对象动态出现个数，进而基于均匀分布的策略预测出该小室内众包对象空间分布。

对于众包对象的属性参数预测，DPRF基于当前时间戳内已有众包对象的属性参数，采用正态分布的策略完成对应的众包对象属性参数预测。

3.1.1 众包对象空间分布预测

时空众包中众包任务和工人的动态出现具有相似性，本文采用相同的方法预测众包任务和工人。DPRF中众包对象的空间分布预测可分为三步：

1）基于在线随机森林模型初步预测小室cell内的众包对象个数。

在时空众包环境下，一个区域内众包对象的动态出现与该区域的时空属性息息相关，本文选取了星期WEEK、一天中的时间段TQ、天气WEA、区域的繁华程度BQ，作为训练样本的四类特征，即随机森林中决策树分支的影响因素。其中对于时间段TQ，本文以一个小时为间隔；对于天气WEA，划分为晴、大雨、中雨、小雨、阴五种状况；对于区域的繁华程度BQ，本文也将其划分为5种等级。

基于上述四类特征本文选取分类回归树（ClAssification and Regression Tree，CART）作为随机森林回归预测算法的基本单元，对于CART 则采用最小均方差原则作为决策树节点划分的依据。在决策树生成过程中，对应的任意划分点s两边划分成的数据集D1和D2，使得D1和D2各自对应的均方差最小，同时D1和D2的均方差之和最小。即节点选择条件为：

其中：c1为D1数据集的样本输出均值，c2为D2数据集的样本输出均值。

进而确定随机森林中决策树的个数numDT、每个决策树的特征数量numSF以及建立决策树时递归次数即树的深度numREC，据此，从样本数据集中有放回的随机抽取numDT次，每次从抽取的样本中选取numSF个特征用于构建决策树，进而构建基于CART的随机森林。

对于小室cell，随机森林算法将所有决策树的预测结果的平均值作为最终预测结果，即：

其中preDTi表示第i棵决策树的预测结果。

最终可得到n×n的网格图中小室celli的初始预测结果numcelli，其中numw celli表示该小室内众包工人的初始预测数目，numm celli表示该小室内众包任务的初始预测数目。

2）基于滑动窗口确定每个小室cell内的众包对象个数。

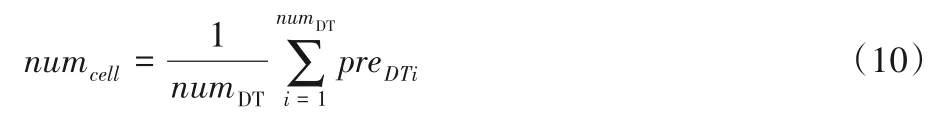
时空众包中空间位置相近的区域，众包对象的出现往往具有相似性，由此DPRF 采用滑动窗口的方式，在初始预测的基础上，针对每个小室，结合滑动窗口对应相邻小室的预测结果，根据滑动窗口的权重，进行加权计算，完成众包对象数目的预测（对于网格图边缘的小室，无法满足滑动窗口，则取其剩余相邻的小室进行预测）。

以图1（a）为例，小室cellA0作为待预测区域，Scell={cellA1，cellA2，cellA3，cellA4，cellA5，cellA6，cellA7，cellA8}作为滑动窗口涉及的相邻小室；图1（b）表示滑动窗口对应的权重分布，cellA1、cellA3、cellA6、cellA8小室的权重为w1，cellA2、cellA4、cellA5、cellA7小室的权重为w2，权重分布满足0 ＜w1 ＜w2 ＜1。预测小室cellA0的众包对象数目为：

其中：Nw为滑动窗口中小室的数目（本例中Nw=9），表示滑动窗口对应小室的权重。cellA0中预测的众包工人数目为，众包任务数目为。

图1 小室cell的待预测区域和滑动窗口对应的权重分布示意图Fig.1 Area to be predicted of a cell and weight distribution corresponding to sliding window

3）采用均匀分布的策略完成众包对象的空间分布预测。对于网格图中每个小室cell内预测的众包对象，均匀分布在小室四周的网格线上，完成空间分布预测。

3.1.2 众包对象参数属性预测

对于网格图中小室celli内预测的众包对象的参数属性，即众包工人的任务成功率sw和众包任务的回报值gm，ORFRP算法采用正态分布的方式为小室celli内预测的对象设置属性参数。以当前时间戳小室celli内众包对象平均属性参数值作为正态分布的均值，以σw作为工人任务成功率的方差，σm作为任务回报值的方差。公式表达如下：

其中：agm celli表示小室celli当前时间戳内众包任务的平均回报值，asw celli表示小室celli当前时间戳内众包工人的平均任务成功率。

综上，根据每个小室celli内的众包对象的空间分布和属性参数分布完成该小室内众包对象的预测，进而基于每个小室的预测情况完成整个n×n网格图中下一时间戳内的动态出现众包对象预测。

3.2 基于GRU的工人移动轨迹预测算法（WMTP算法）

首先定义众包工人w在时间戳Ti时的轨迹点：

其中：dirw表示工人的移动方向，xc和yc表示工人在二维网格图中的横纵坐标值。

WMTP算法基于RNN-GRU循环神经网络回归预测模型，根据众包工人w的移动轨迹序列Seqw预测下一时间戳Tc+1任务分配时工人w所处的空间轨迹点。工人移动轨迹序列Seqw由连续n个时间戳的工人的移动轨迹点组成，即Seqw=作为RNN-GRU 预测网络的输入，预测网络输出下一时间戳Tc+1的轨迹点。据此，工人移动轨迹预测模型的表达式为：

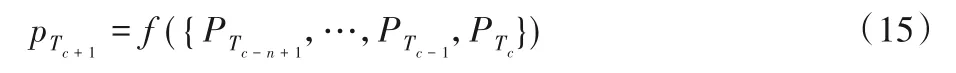
本文采用many to one 类型的单层RNN-GRU 循环神经网络，其展开图如图2 所示。在模型训练和预测的过程中，RNN-GRU 模型每次输入样本为连续n个时间戳的工人移动轨迹点序列Seqw（step=n），每个轨迹点pTi具有Ti，dirw，xc，yc四项特征。

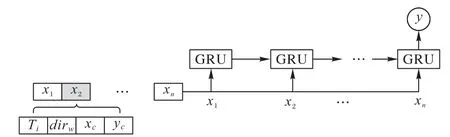
图2 GRU循环神经网络时序预测展开图Fig.2 GRU recurrent neural network time series prediction expansion diagram

对于样本输入中任意时刻Ti的轨迹点pTi，GRU 处理过程如图3所示，GRU输入包括当前轨迹点输入xt(xt=pTi)和上一时刻的隐藏状态ht-1（h0=0），GRU 首先基于ht-1和xt通过更新门zt确定上一时刻隐藏状态中信息的保留程度：

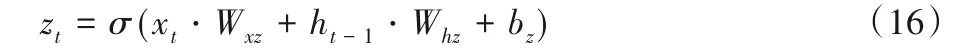
其中：σ表示sigmod 函数，Wxz、Whz和bz对应zt计算时权重和偏执。同时根据重置门rt将当前输入xt和上一时刻隐藏状态ht-1中信息结合：

其中Wxr、Whr和br对应rt计算时权重和偏置。进而基于重置门rt和当前输入xt确定候选隐藏状态：

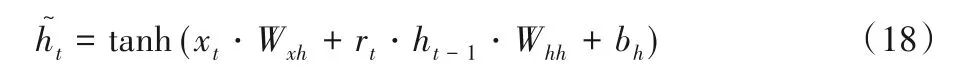
其中Wxh、Whh和bh对应计算时权重和偏置。最后基于上一时间戳隐藏层状态ht-1和当前时间戳候选隐藏状态确定当前隐藏层状态ht：

图3 GRU神经元内部结构Fig.3 GRU neuron internal structure

如果本次样本输入的是最后一个时刻xn的数据，则预测模型在本次处理得到隐藏状态ht的基础上添加全连接层输出y，否则ht作为下一时刻的隐藏状态输入。

在训练过程中选用均方差函数作为损失函数，即预测值与真实值之差的平凡的期望值，根据BPTT（Back Propagation Through Time）算法计算梯度，进而更新模型的参数，完成模型训练。

由此，根据上述训练完成的RNN-GRU 模型预测出当前时间戳内已有众包工人w在下一时间戳时所处空间位置是lnw(xc+1，yc+1)的轨迹点pTc+1。完成已有众包工人在下一时间戳内分布预测。

3.3 基于KM算法在线任务分配

在时空众包任务分配中，将众包任务和工人分别看作是二分图的两个点集，可分配任务工人匹配对集合MP看作边集，对应任务工人匹配对综合效益CB作为边的权重，执行二分图最优匹配算法（KM算法），以完成三方综合效益全局优化的任务分配。

在本文提出的基于预测分析的全局优化在线任务分配算法GOMA中，首先构建基于预测分析的二分图模型，将当前待分配任务集合Mt和DPRF 预测新出现的任务集合Mnt看作是二分图的一个点集Vm。当前待分配工人集合Wt、DPRF 预测新出现的工人集合Wnt以及基于WMTP 算法预测出下一时间戳众包工人集合Wmt看作是二分图的另一点集Vw。其中：Wmt是将WMTP 算法预测出工人w在下一时间戳所在空间轨迹点pTc+1看作是处于lnw位置，属性参数相同的众包工人wm。工人点集中每一个工人与其最适接单范围内的任务进行预匹配，构成可分配任务工人匹配对mp，进而根据任务工人匹配对集合MP连接二分图。并假设当前时间CT为分配时间，计算每个任务工人匹配对的Up、TWm、COw三项指标，进而计算综合匹配效益CB，以CB作为边的权重。

最后基于上述搭建的二分图模型执行KM 算法，在算法匹配结果Sp中，将众包任务和工人均处于当前时间戳内的匹配对mp加入分配结果集R中。对于含有预测任务或工人的匹配对，则表明这些众包对象在后期分配，会使得全局分配效果更优，故当前时间戳不予分配。

3.4 算法具体实现

GOMA伪代码如下：

Input：众包任务集合M，众包工人集合W，综合收益指标CB的计算函数、已训练完成RNN-GRU预测模型；

Output：任务分配的结果集R。

GOMA 每一时间戳内的算法时间复杂度分析如下：DPRF 的时间复杂度是O(numSF×numREC)，其中numSF是随机森林中决策树的特征数量，numREC是决策树的深度。基于GRU 的工人移动轨迹预测算法（WMTP 算法）的时间复杂度为O(numPW×step)，其中numPW是当前待预测的工人数目，step是GRU 网络中输入轨迹序列中轨迹点的数目。进而执行带权二分图最优匹配算法的时间复杂度是O(|Vm|2×|Vw|)，其中|Vm|是二分图边集的容量，|Vw|是二分图点集的容量。所以 GOMA 一轮任务分配的时间复杂度是：max(O(numSF×numREC)，O(numPW×step)，O(|Vm|2×|Vw|))。

3.5 算法举例

假设当前时间戳Ti=15 内待分配任务有m1、m2，待分配工人有w1、w2，平台工人的接单范围半径均为rw=1.5，时间戳时间间隔|Ti|=3，工人移动速度speed=0.5 单位长度/单位时间，工人的移动成本per=1 单位成本/单位长度，任务工人匹配对综合效益CB=0.5Up+0.15AT'm+0.2/MT'm+0.15CO'w，AT'm=ATm/9，MT'm=MTm/4，CO'w=COw/4.5。工人属性参数见表1，任务属性参数见表2。

表1 工人信息Tab.1 Information of workers

表2 实验数据参数Tab.2 Parameters of experimental data

按照GOMA的执行步骤：

1）基于DPRF预测下一时间戳Ti+1内该平台上新发布任务mn1、mn2和新上线工人wn1。

2）基于WMTP 算法预测当前时间戳的待分配工人w1、w2在下一时间戳空间分布点wm1、wm2。

3）当前对象和预测对象的分布情况如图4 所示，构建二分图模型并计算权重。权重计算以为例，Up=0.4875，2/3，。

图4 众包任务和众包工人分布示意图Fig.4 Crowdsourcing tasks and distribution of crowdsourcing workers

二分图模型如图5 所示，然后执行带权二分图最优匹配算法（KM算法），得到最优匹配集：

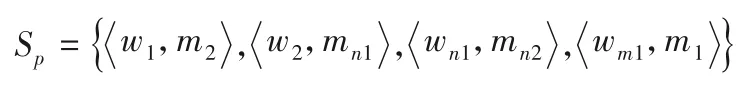
图5 众包任务和众包工人匹配示意图Fig.5 Matching of crowdsourcing tasks and crowdsourcing workers

4 实验分析

4.1 实验数据与环境

为验证本文算法的有效性，从微软开源数据集T-Drive 项目中获得出租车的行驶轨迹点数据作为众包工人的初始数据集，通过相应的预处理得到15 174 组数据；从时空众包平台gMission［23］上爬取了17 296条记录，进行相应处理取得众包任务的相应数据。将任务和工人的位置映射在100×100 的网格图中，得到任务和工人的二维坐标。从处理后的数据集中基于均匀分布的原则选取13 000 组众包工人和任务进行仿真实验。

本实验在处理器为2.3 GHz Inter Core i5-6300HQ，内存为8 GB 的计算机上运行，操作系统为Windows 10。基于Tensorflow 的上层框架Keras进行模型的搭建。实验使用的编程语言为Python，使用的集成开发环境是PyCharm。

4.2 预测模型参数取值

本文WMTP 算法所设计的工人轨迹预测模型为3 层，分别为输入层、GRU 隐藏层和输出层。本文设置GRU 隐藏层神经元节点数CELL_SIZE、输入层步数step作为模型可调节参数，均方差（Mean Squared Error，MSE）作为模型的评估指标，以确定最佳的模型参数取值。

设置输入层步数step从3 到7，隐层神经元节点数CELL_SIZE 为同一step下的最优值，不同step对应的模型均方差如图6所示。

随着输入的维度越大，模型的复杂程度越高，预测效果越好，但当输入维度过高时模型会发生过拟合。根据实验结果选取step=5作为输入层序列Seqw中的轨迹点数量，此时模型的预测效果最好。

将连续5 组工人（其中每组包含工人数100 名）的平均移动轨迹点组成轨迹序列Seqw作为网络输入，设置5～15 不同的GRU 隐层神经元节点数，评估模型的预测效果，实验结果如图7 所示。由图7 可知，当隐层神经元数目为11时模型均方差最小。表明当输入层step=5时，隐层神经元个数为11，模型的预测效果最佳。

图7 GRU神经元均方差分布Fig.7 MSE distribution of GRU neurons

4.3 GOMA有效性实验

本实验从任务分配成功率、分配的平均综合效益、工人平均机会成本三个方面对贪心算法、随机阈值算法和GOMA 进行比较分析，实验数据的参数设置如表2，其中任务回报值gm和工人的任务成功率sw满足正态分布。

1）在任务分配成功率方面，具体实验结果如图8 所示。GOMA 始终优于贪心算法和随机阈值算法。当工人数量|W|增加时，三种算法的任务分配成功率均由增长逐渐趋于稳定；当任务数量|M|增加时，由于工人数量相对逐渐减少，三种算法的任务分配成功率均有一定程度的降低；当任务的有效时间上限ETm增加时，待分配任务可参与多轮任务分配，GOMA和贪心算法均有小幅度增长，但随即阈值算法的波动较大；当工人的接单范围半径rw增加时，GOMA 的任务分配成功率增速明显高于贪心算法和随机阈值算法。

图8 三种算法在任务分配成功率方面的实验结果Fig.8 Experimental results of three algorithms in success rate of task allocation

2）在平均综合效益方面，具体实验结果如图9 所示。GOMA 整体相对稳定，对比贪心算法和随机阈值算法，平均综合效益有大幅度的提升。工人数量|W|与任务数量|M|对GOMA 和贪心算法的影响不大，随机阈值算法由于随机选取阈值，平均综合效益变化较大；当任务的有效时间上限ETm和工人的接单范围半径rw增加时，可分配的任务工人匹配对数量增加，GOMA和贪心算法的平均综合效益均有小幅度增长。

3）在工人平均机会成本方面，具体实验结果如图10 所示。当工人数量|W|和任务数量|M|增加时，GOMA 的工人平均机会成本有小幅度变化，但一直明显优于贪心算法和随机阈值算法；当任务的有效时间上限ETm增加时，GOMA 处于较为稳定状态，贪心算法和随即将阈值算法的工人平均机会成本逐渐增大；当工人的接单范围半径rw增加时，贪心算法和随机阈值算法的工人平均机会成本增速明显高于GOMA。

图9 三种算法在平均综合效益方面的实验结果Fig.9 Experimental results of three algorithms in average comprehensive benefit

从以上实验不难发现：

1）在任务分配成功率方面，GOMA 始终优于贪心算法和随机阈值算法。

2）在分配的平均综合效益方面，工人数量|W|和任务数量|M|的变化对GOMA 影响不大，当任务的有效时间上限ETm和工人的接单范围半径rw增加时，GOMA 分配的平均综合效益逐渐增长并趋于稳定，对比贪心算法和随机阈值算法具有明显的优势。

3）在工人的平均机会成本方面，当工人数量|W|、工人的接单范围半径rw增加时，三种算法工人的平均机会成本均逐渐增加，但贪心算法和随机阈值算法的增速明显高于GOMA。当任务数量|M|增加时，三种算法的工人平均机会成本均逐渐降低，但GOMA 工人的平均机会成本低于另外两种算法。当任务的有限时间上限ETm增加时，GOMA 较为稳定，但随机阈值算法的波动比较大。

综上，可以看出本文提出的GOMA 具有较好的实际应用价值，能有效地解决本文研究的CMA-MCB问题。

图10 三种算法在工人平均机会成本方面的实验结果Fig.10 Experimental results of three algorithms in average opportunity cost of workers

5 结语

本文研究了时空众包环境下面向全局优化的在线任务分配问题。首先采用基于在线随机森林的众包对象动态预测算法（DPRF）预测下一时间戳内众包对象动态出现的情况，然后利用基于GRU的工人移动轨迹预测算法（WMTP）预测众包工人的移动轨迹，最后结合当前众包对象的分布情况，基于带权二分图最优匹配算法进行任务分配，能够有效地提高任务分配的综合效益。通过实验证明了本文所提算法在任务分配率、分配的平均综合效益、工人的平均机会成本方面具有较好的性能表现，能够有效地解决时空众包中全局优化的在线任务分配问题。未来的时空众包研究，可从以下两个方面展开：1）针对众包对象的分布情况预测，进行多步时间戳预测，进一步优化任务分配的效果；2）引入强化学习、预训练等深度学习方法优化预测模型，进一步提高众包对象分布情况预测的准确率。