基于改进粒子群优化算法的牙齿正畸路径规划方法

徐晓强，秦品乐，曾建朝

（中北大学大数据学院，太原 030051）

（*通信作者电子邮箱zjc@nuc.edu.cn）

0 引言

正畸（Orthodontics）又称牙齿矫正，是指利用各种牙齿矫治器对患者牙齿的位置进行重新排列，使其恢复到与正常牙齿形态相对一致的过程［1］。牙齿矫治器包括传统有托槽矫治器、无托槽隐形矫治器等。近年来，随着无托槽隐形矫治器相较于前者具有更舒适、美观、节约矫治时间、容易清洁等特点［2］，并且患者通过无托槽隐形矫治系统可以提前看到矫治完毕后的牙齿具体排列情况。因此，越来越多的患者选择无托槽隐形矫治器进行牙齿矫正，这使得运用计算机技术对按数学模型排列的虚拟牙齿正畸技术成为研究的热点。复杂的牙齿正畸路径规划作为上述研究热点的一个重要步骤，既要保证矫治路径具有可行性，同时也要保证矫治结果具有优化性。专业地说，牙齿正畸路径规划是保证患者的全部牙齿矫治过程在符合正畸学的前提下，使多颗牙齿在经过数个矫治阶段后达到最终理想位置，并且在该过程中相邻牙齿间不发生碰撞，因此需要寻找一条尽可能减少患者矫治时间、移动距离、旋转角度等因素的最优路径作为最终牙齿正畸移动路径。文献［3］提取了人工牙三维三角网格数据的特征点建立了牙齿选择系统，通过计算机数控技术完成了全口义齿的虚拟排牙方法。文献［4］提出单颗牙齿自动分割方法优化了传统方法，通过搜索分割路径、图像形态，拟合牙弓线，匹配最优路径确定牙缝边界路径，细化封闭分割轮廓完成整个牙齿的分割。此方法对于严重畸形的牙齿具有较好的正畸效果。文献［5］提出了一种基于数字图像与计算机断层扫描模拟的虚拟近似真实正畸牙齿移动，并通过给牙齿特定位置施加力来减少平移及旋转次数。文献［6］根据压力和张力与特定的信号传导相关因子，建立了局部梯度来重塑牙周，以更快地移动牙齿，减少治疗时间和依赖时间的不良后果。

随着对遗传算法、神经网络算法等启发式算法的深入研究，发现上述算法大多存在计算量大、操作复杂、算法运行时间过长等问题，越来越多的研究者提出运用粒子群优化（Particle Swarm Optimization，PSO）算法来解决路径规划的相关问题。PSO 算法是Eberhart等［7］通过模拟鸟类行为规律，提出的一种全局优化算法。PSO 算法因其结构简单、效率较高等优点已经广泛应用于各类优化问题［8-9］，近年来对改进粒子群算法在路径规划领域的研究陆续被提出。文献［10］提出了斥力场下粒子群，利用栅格法进行初步规划以及根据不同的障碍物所构建数学模型、适应度函数，从而得到了移动机器人最优路径。文献［11］在光栅化的基础上构建了包括随机地表模型、山地地形模型的数学模型，并分析了路径威胁因素，引入遗传算法的思想改进了粒子群算法最终得到了低威胁的干扰机路径。文献［12］提出了一种基于高斯参数更新规则和粒子重新初始化的改进粒子群算法，从缩短路径长度及提高路径光滑度两方面优化了路径规划问题。文献［13］通过个体粒子进化速度与群体离散度来调整粒子群的惯性权重，以此避免其过早收敛，并利用自然选择方法改进量子行为粒子群的优化算法，将这两种优化的算法引入移动机器人路径规划，并通过实验证明方法的可行性。文献［14］以ER3A-C60 机器人作为研究对象，建立了运动学和动力学模型，用参数合适的PSO算法求得了最小综合误差得到了一条最优轨迹。

受上述改进算法的启发，针对虚拟口腔正畸治疗系统中牙齿移动路径规划问题，本文提出了一种基于正态分布的简化均值粒子群的牙齿正畸路径规划方法。首先建立了单颗牙齿及整体牙齿的数学模型，并将牙齿正畸路径规划问题转化为带约束的优化问题；其次，引入正态分布及均值粒子群，结合简化粒子群的位置项，提出了一种基于正态分布的简化均值粒子群优化（Simplified Mean Particle Swarm Optimization based on Normal distribution，NSMPSO）算法；最后，构造了包含平移路径长度、旋转角度、碰撞检测以及牙齿在单阶段的移动量、旋转量的高安全性的适应度函数，实现了牙齿正畸移动路径的规划。在三大基准测试函数上将NSMPSO 算法与其他三种粒子群算法进行对比，结果表明，本文改进的算法在收敛速度和收敛精度上均有明显的提高，通过Matlab 的仿真实验表明了利用该数学模型和改进算法求得的最优路径安全可靠，可以为医生辅助诊断提供有效的帮助。

1 建立数学模型

1.1 单颗牙齿及整体牙齿的数学模型

本文以分割后的牙齿为研究对象。首先，采用有向包围盒（Oriented Bounding Box，OBB）对分割后的单颗牙齿建立包围盒，以包围盒的中心点作为牙齿的特征点建立局部坐标系，X、Y、Z轴的方向根据单颗牙齿包围盒的长宽高来确定。图1为尖牙、侧切牙、后磨牙在三维数学模型下单颗牙齿包围盒的局部坐标系。然后，以全部牙齿为目标，选取两颗后磨牙、两颗尖牙的特征点所确定的平面作为基准面来建立牙齿整体的世界坐标系。图2 为整体牙齿在三维数学模型下的世界坐标系。最后，用每颗牙齿的包围盒及中心点代替牙齿进行整个矫正过程的展示，可以更直观、形象地了解每个阶段内的牙齿位置的变化情况。在某一矫正阶段内，由于全部牙齿的移动和旋转是同时进行的，则可将该阶段的牙齿移动路径离散化表示为一系列路径点的连线。

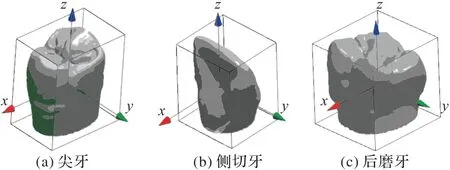
图1 单颗牙齿的三维坐标系Fig.1 Three-dimensional coordinate system of single tooth

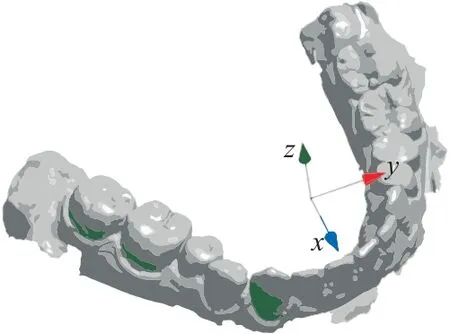
图2 整体牙齿数学模型Fig.2 Mathematical model of whole teeth

1.2 牙齿移动路径规划的数学建模

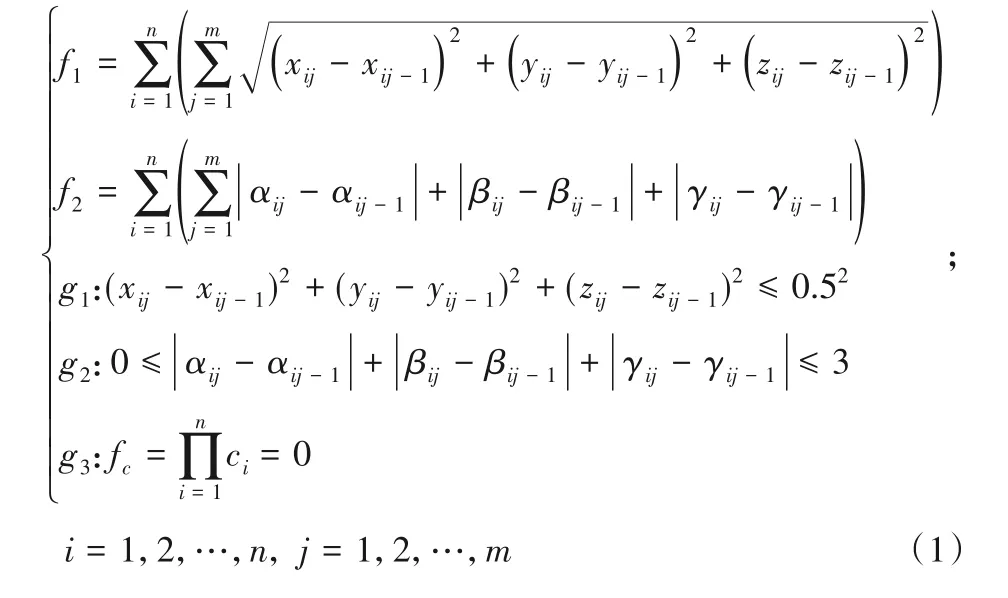
将n颗牙齿的移动路径规划分为m个阶段，m由每个阶段可移动、旋转的最大值及医生经验共同决定。牙齿在矫治过程中，在满足单阶段内患者可以承受的牙齿最大移动量、旋转量并且无碰撞发生的前提下，确定每个阶段的所有牙齿的位置信息，最终规划出一条牙齿从初始位置到最终位置的最短路径，即为可执行的牙齿移动最优路径。因此可将牙齿正畸路径规划问题等价为带约束的优化问题：其中：n为牙齿个数，m为矫治阶段数。(xij，yij，zij)表示第i颗牙齿在第j个矫治阶段结束后的位置坐标，目标函数之一f1表示牙齿平移路径长度，是通过计算空间中两点间的欧氏距离构建的。计算患者所有牙齿在全部矫治阶段内的移动量之和，值越小表示牙齿在矫治过程中需要移动的量越小，从而减少了患者的矫治时间。目标函数f2表示牙齿旋转角度，(αij，βij，γij)为第i颗牙齿第j个阶段时包围盒的三边与世界坐标系的三轴之间的夹角。单颗牙齿包围盒的局部坐标轴X1、Y1、Z1在全部牙齿建立的世界坐标轴X2、Y2、Z2的投影分别为X1X2、Y1Y2和Z1Z2，组成的三个夹角即为α、β、γ，计算患者全部牙齿在整个矫治阶段内的旋转量之和即为目标函数二。根据正畸学及医生临床经验可知，每颗牙齿在某个矫治阶段内移动范围不能大于0.5 mm、旋转角度不能超过3°。考虑到每颗牙齿在规定范围内进行移动或者旋转之后，可能出现某颗牙齿与左右相邻的牙齿发生碰撞挤压导致矫治失败的情况，因此在每个矫治阶段检测牙齿间是否发生碰撞至关重要。综上，用g1、g2、g3表示在对目标函数f1、f2进行优化时的约束条件。约束条件g1是限制每颗牙齿在前后两个阶段的移动量小于每个阶段单颗牙齿能够承受的最大移动量；约束条件g2是限制每颗牙齿在前后两个阶段的旋转量小于人类能够承受的每个阶段的最大旋转量；约束条件g3是检测矫治过程中相邻牙齿是否碰撞，式中ci表示判断第i颗牙齿与其左右相邻的牙齿是否发生碰撞。如果两颗牙齿没有发生碰撞，则ci等于0；否则ci不为0。因此使得约束条件g3中的fc等于0，则满足牙齿在矫治过程中无碰撞发生。

2 用NSMPSO算法实现牙齿正畸路径规划

2.1 粒子群算法

在D维搜索空间中，随机初始化z个粒子，这些粒子可视为优化问题的可行解，并根据预先设定的适应度函数来评价粒子所在位置的好坏。粒子i的当前位置为Xi=(xi1，xi2，…，xiD)，当前速度为Vi=(vi1，vi2，…，viD)。在每次迭代中，pi=(pi1，pi2，…，pid，…，piD)表示粒子迄今为止经历的最优位置，pg=(pg1，pg2，…，pgd，…，pgD)表示整个种群迄今为止经历的最优位置。粒子的速度和位置的更新公式如下：

其中：下标i=1，2，…，z，下标d=1，2，…，D，t是当前迭代次数，w是惯性权重。c1和c2是学习因子，r1、r2～U（0，1）的随机数。为了使粒子在搜索空间内充分搜索，在迭代过程中限定粒子速度向量上下限为［vmin，vmax］，位置向量上下限为［xmin，xmax］。

2.2 基于正态分布的简化均值粒子群算法

在D维搜索空间中，粒子均按照一定的速度和方向运动，因此忽略粒子在运动过程中的体积与质量，可将其看作一个点。在连续解空间过程中，粒子逐渐向全局最优解附近靠拢，可将多维可行解空间看作服从多元正态分布。在真实的迭代过程中，粒子在可行解空间的分布不完全意义上服从正态分布，相比之下仍存在一定的偏离，但鉴于这一部分的偏差的存在对整体实验结果的影响不大，可忽略不计，并且绝大多数粒子的分布是服从正态分布的，所以引入正态分布作为真实粒子在搜索空间分布的近似值是合理可行的。因此，本文引入正态分布和均值粒子群［15］的思想，结合简化粒子群［16］中的位置项，提出了一种基于正态分布的简化均值粒子群（NSMPSO）算法。改进后粒子的位置公式如式（4）所示：

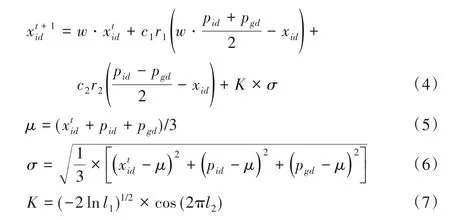
其中w为惯性权重。式（4）将简化粒子群的位置项扩展为四项：第一项表示向粒子当前位置学习项。第二、三项中用粒子个体最优位置、种群全局最优位置的线性组合取代粒子的个体最优位置和全局最优位置，用惯性权重调整影响大小。第四项为正态分布项，其中，μ表示粒子当前位置、粒子个体最优位置及全局最优位置三者的平均值，根据式（5）计算；σ表示粒子当前位置、粒子个体最优位置及全局最优位置三者的标准差，根据式（6）计算；l1和l2是［0，1］范围内均匀产生的随机数，K是由指数函数和三角函数组成的常数项，用来控制标准差的影响程度，根据式（7）计算。为了避免出现标准差为0的情况，规定当标准差阈值t小于1E-05时，标准偏差的值取平均值的一半。综上所述，本文提出的NSMPSO 算法增强了种群的多样性，加入正态分布项进一步改善了PSO 算法在解决高维问题时求解精度不高、容易陷入局部最优等缺点。

2.3 构造适应度函数

构造一个合理的、安全性高的适应度函数不仅可以作为衡量优化得出的牙齿正畸移动路径优劣程度的标准，同时也是检测本文改进的粒子群算法在收敛速度及收敛精度方面是否有所提高的判断准则。根据牙齿正畸移动路径规划问题的特点，本文对它的评价取决于5 个方面，分别是平移路径长度、旋转角度、是否碰撞以及牙齿在单阶段的移动、旋转量。

平移路径长度评价函数对应目标函数f1，旋转角度评价函数对应目标函数f2，用式（1）中的g1、g2表示对牙齿在矫治过程中某一阶段移动距离和旋转角度的限制约束。本文对约束条件g3通过添加常数项进一步改进，函数f3作为评价是否发生碰撞的标准，定义如下：

其中，S表示给定的一个较大常数项，其作用是当相邻的牙齿发生碰撞时，较大的常数S可以使得整个f3的值明显增大。如果两颗牙齿没有发生碰撞，则f3=0。

综上，结合f1、f2、f3、g1、g2定义本文算法的适应度函数为：

其中，i=1，2，…，z；δ、η、λ、μ、θ分别为路径长度、旋转角度、是否碰撞以及牙齿在单阶段内的移动、旋转量在适应度函数中的权重，且为大于0 的实数。式（9）中f1和f2是基于目标函数1 和2 构建的，设置其权重略大于f3、g1、g2的权重。分析适应度函数Fi可知，函数值越小说明得到的牙齿正畸路径越优。

2.4 NSMPSO算法在路径规划中的实现

2.4.1 解的编码问题

PSO 算法采用实数编码，一个粒子代表着所有牙齿在全部阶段内的矫治结果，也就是说每个粒子对应着一个可行解。由于每个粒子的位置由每颗牙齿在每个矫治阶段中平移所确定的坐标(xij，yij，zij)和旋转所确定的(αij，βij，γij)组成。牙齿个数为n，矫治阶段数为m，因此粒子的位置是6×n×m维变量。这样，粒子的编码结构如下所示：

2.4.2 算法实现的具体步骤

步骤1 获取患者牙齿数据，提取牙齿特征点作为初始位置坐标，本文采用β函数来拟合理想牙弓曲线，从而确定牙齿矫正结束后的最终位置坐标［17］，公式如下：

其中：W是患者两个磨牙特征点之间的距离，H是患者中切牙特征点到两颗磨牙特征点之间连线的最短距离，e是将患者尖牙的特征点坐标代入式中所确定。

步骤2 按照2.4.1节对粒子进行编码，初始化种群并设定相关参数，其中包括患者牙齿个数n，需要矫治阶段数m，种群大小z，每个粒子维数D，最大迭代次数Tmax。初始化粒子的位置，公式如下：

其中，r为［0，1］区间的随机数。

步骤3 根据式（9）计算每个粒子的适应度值，并更新粒子的个体最优值和全局最优值。

步骤4 根据式（5）计算粒子当前位置、粒子个体最优位置及全局最优位置的平均值，根据式（6）计算三者的标准差，根据式（7）计算常数项K。添加正态分布项，对种群中的每个粒子根据式（4）进行位置更新。

步骤5 判断算法迭代次数是否达到所设定的最大迭代次数，若是，停止迭代，输出牙齿正畸移动最优路径；否则，返回步骤3）继续执行。

算法流程如图3所示。

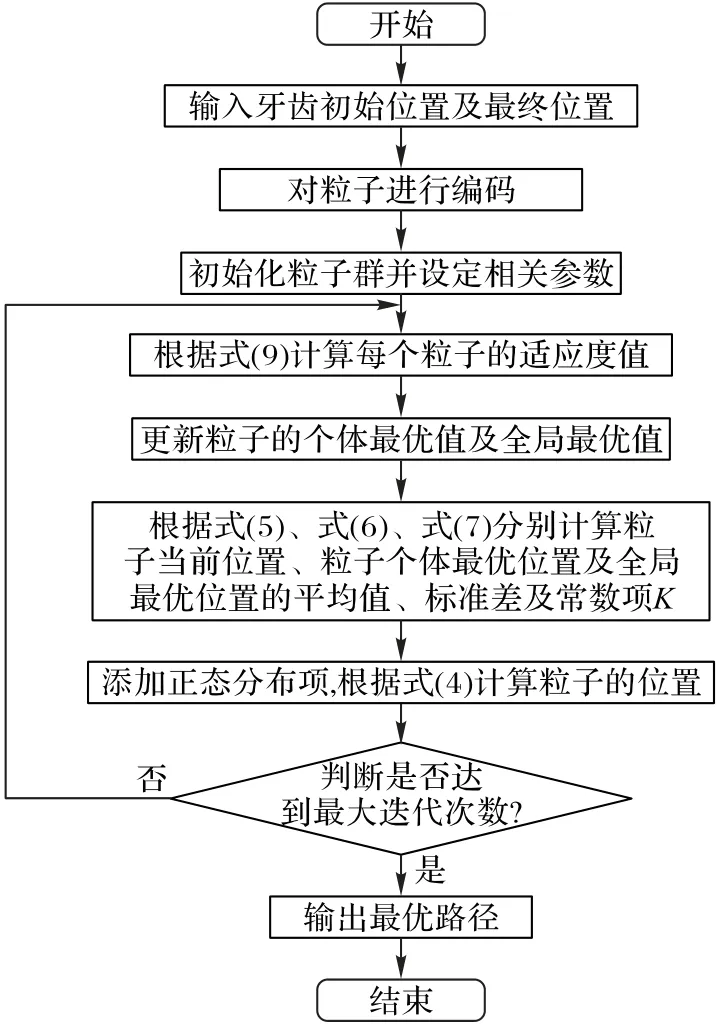
图3 NSMPSO算法流程Fig.3 Flowchart of NSMPSO algorithm

3 实验环境及分析

3.1 测试函数

为了验证本文提出的NSMPSO 算法在收敛精度及收敛速度方面上的提升，将NSMPSO 算法与基本粒子群优化（PSO）、均值粒子群优化（Mean Particle Swarm Optimization，MPSO）和动态调整惯性权重的简化均值粒子群优化（Simplified Mean Particle Swarm Optimization with Dynamic adjustment of inertia weight，DSMPSO）算法进行对比。本实验选取三大基准函数作为测试函数，其中：Sphere 函数是单峰函数，主要用于检验算法的收敛速度和求解精度；Ackley 函数和Griewank 函数是多峰函数，主要用于检验算法的全局搜索能力。测试函数描述如下。

1）Sphere测试函数：

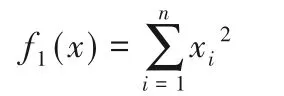
其中，搜索区间为［-100，100］，当f1(x)=0时，Sphere 测试函数取得全局最优值。

2）Ackley测试函数：

其中，搜索区间为［-32，32］，当f2(x)=0时，Ackley 测试函数取得全局最优值。

3）Griewank测试函数：

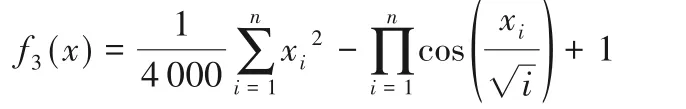
其中，搜索区间为［-600，600］，当f3(x)=0时，Griewank 测试函数取得全局最优值。

3.2 参数设置

在实验中，测试函数的维数D=30，最大迭代次数genmax=150，种群粒子数m=30。对于PSO 算法和MPSO 算法，w=0.8、c1=c2=2。对于DSMPSO算法，c1=c2=2，wmax=0.9、wmin=0.4、f1(x)==0.1、a=1、b=2。对于NSMPSO 算法，w取［0.4，0.9］区间的随机数，c1=c2=1.494。

3.3 实验结果分析

3.3.1 收敛性分析

本实验为了验证NSMPSO 算法的收敛性，分别与PSO、MPSO、DSMPSO 算法在三大测试函数上进行对比分析。四种算法迭代150次的收敛效果如图4所示。

从图4中可以看出，对于单峰Sphere 函数，基本PSO 算法由于全局搜索能力较弱，陷入局部最优导致算法过早停滞，在迭代150 次后未收敛，而MPSO 算法收敛速度较慢，DSMPSO、NSMPSO 算法均能较快找到全局最优解，相比之下，NSMPSO算法适应值小于其他三种算法，求解精度相对较高。对于多峰Ackley 函数，基本PSO 算法由于难以处理复杂的多峰函数导致算法停滞，MPSO 算法由于跳出局部最优能力较弱，经过140 次迭代后适应值开始趋于稳定，相比其他两种改进算法，收敛速度过慢，而DSMPSO 和NSMPSO 算法均能在50 次内到达全局最优值或者达到最优值附近可接受的范围内，分别在40 次、25 次左右开始趋于收敛。对于多峰Griewank 函数，基本PSO 算法在迭代150 次过后，整体适应值变化不大，没有达到收敛精度。MPSO 算法在解决复杂多峰函数时稳定性不强，DSMPSO 算法以及NSMPSO 算法分别在迭代20 次、15 次左右后适应值稳定收敛，从图4（c）可知，NSMPSO 算法找到全局最优解所需迭代次数最少，收敛速度最快。

综上所述，本文提出的基于正态分布的简化均值粒子群算法（NSMPSO）无论对于单峰函数还是对于多峰函数来说，在寻找最优解过程中均能有效地避免种群陷入局部最优解，并且能够在较少的迭代次数内达到稳定收敛，比其他PSO 算法具有更快的收敛速度，在求解精度方面也较为出色，全局搜索能力更佳。

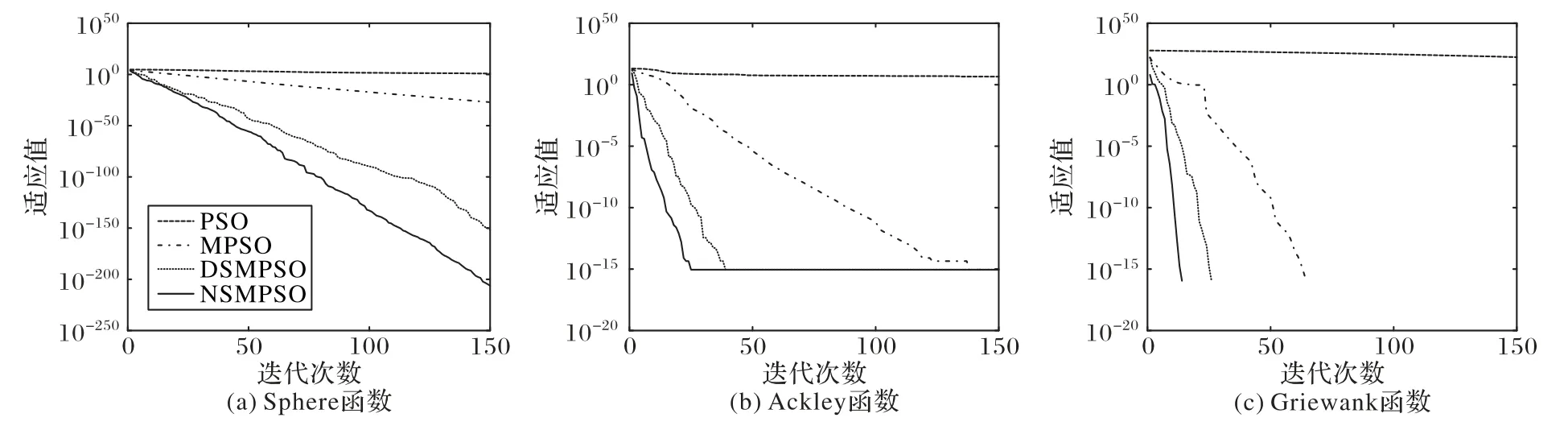
图4 三个函数收敛曲线对比Fig.4 Convergence curve comparison of three functions

3.3.2 有效性分析

为了进一步验证本文提出的NSMPSO 算法的有效性，选取某患者下牙颌14 颗牙齿作为矫治对象，选取牙齿特征点作为初始位置，根据理想牙弓曲线确定牙齿矫治结束时的位置。利用NSMPSO 算法在约束条件g1、g2、g3的约束下对目标函数f1和f2进行优化，从而得到每颗牙齿在每个阶段时的坐标位置，然后在Matlab上进行仿真实验。

首先，牙齿在矫治过程中垂直方向上的移动量较小，因此本实验忽略牙齿在垂直方向上的移动，将原本为一条三维空间的牙弓曲线投影到由患者两颗磨牙、两颗尖牙以及中切牙所确定的牙颌平面上，从而简化成一条二维平面上的曲线。其次，患者在矫治过程中所有牙齿是同时进行移动、旋转的，并且需要确保过程中牙齿间不能发生碰撞、挤压，否则容易导致矫治失败，这也是将碰撞检测作为牙齿正畸路径规划的重要原因之一。本实验利用OBB 进行碰撞检测，在二维平面上用包围框代替牙齿可以更直观、形象地表示牙齿移动的可行性，确保牙齿正畸的每一阶段都是合理移动的。最后，以理想牙弓曲线作为牙齿正畸的标准，牙齿正畸路径规划的结果如图5所示。

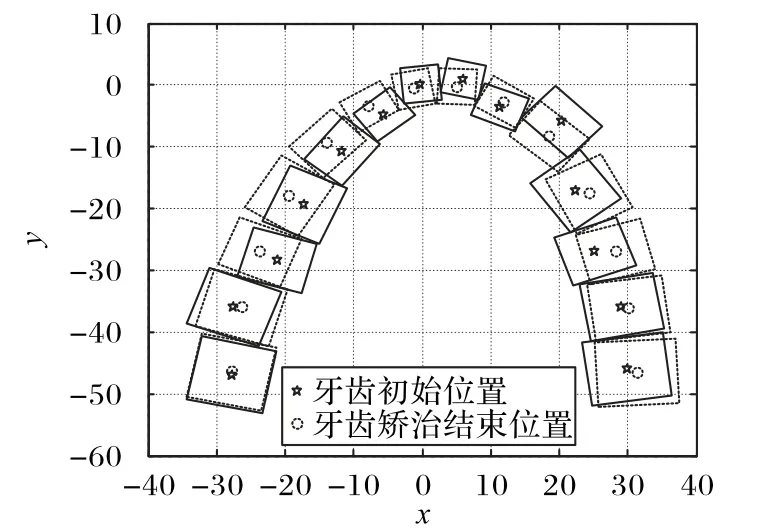
图5 牙齿初始位置与牙齿矫正结束位置对比Fig.5 Comparison of initial position of teeth and position of teeth after orthodontics

图5 表示牙齿初始位置与牙齿矫正结束位置对比，其中实线包围框表示牙齿初始位置，虚线包围框表示牙齿矫正结束位置，包围框的中心点即为每颗牙齿的特征点。为了方便叙述，从左到右依次对牙齿进行编号为1～14，可以看出该患者牙齿排列不齐，里出外进，在一块狭小的区域内多个牙齿相互重叠遮挡。牙齿正畸路径规划过程如图6 所示，其中，牙齿从初始位置到矫正结束一共需要7 步，每一阶段矫正结束时的位置在图6中表示，由于1 号和14 号第一磨牙、2 号和13 号第二磨牙相对移动、旋转较小，因此在矫治第三阶段时第一磨牙、第二磨牙已经达到理想位置，其他牙齿在经过七个阶段的矫治后，牙齿之间排列整齐，没有缝隙，10 号右侧尖牙和4 号前磨牙、3 号前磨牙没有之前被挤出的迹象，并且所优化出来的结果在牙齿矫治过程中，各个相邻的包围框没有发生重叠部分，意味着牙齿之间没有发生碰撞，说明本文提出的改进粒子群算法NSMPSO应用到牙齿正畸路径规划是合理可行的。

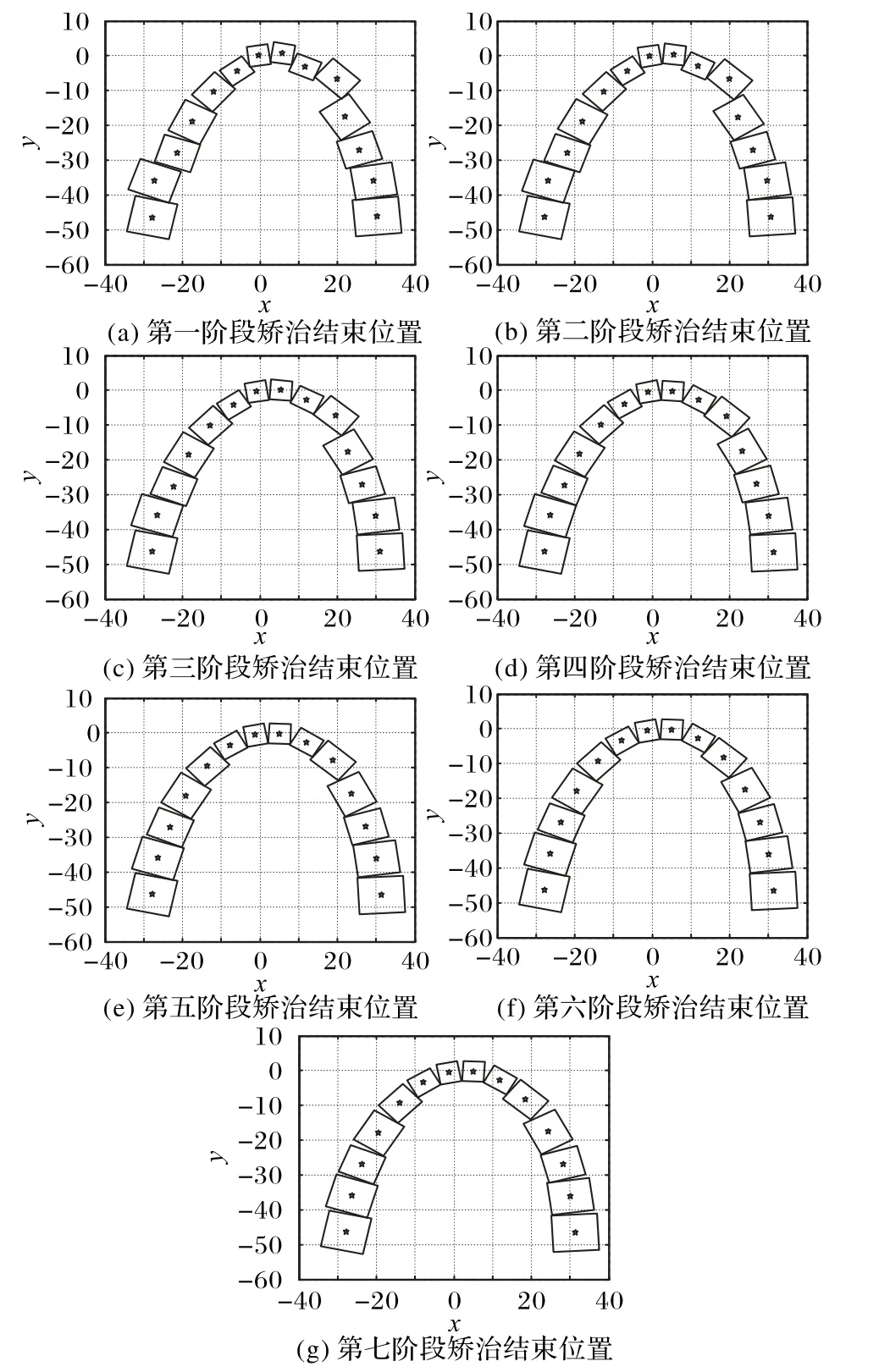
图6 牙齿正畸路径规划结果Fig.6 Orthodontic path planning results

图7 表示四种算法迭代150 次的牙齿正畸路径规划收敛效果对比。可以看出，采用PSO 和MPSO 算法求解牙齿正畸移动最优路径时效果不佳，很难找到全局最优解。与DSMPSO 相比，本文提出的NSMPSO 算法有更快的牙齿正畸路径规划收敛速度，在迭代45 次左右算法开始收敛，表示NSMPSO 算法可以规划出一条有效的牙齿正畸移动最短无碰撞路径。

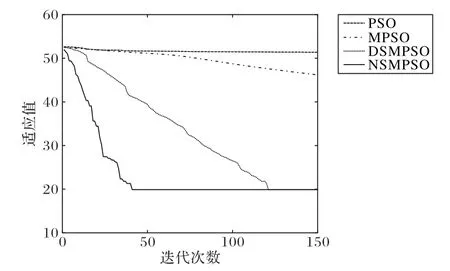
图7 牙齿正畸路径规划收敛图Fig.7 Orthodontic path planning convergence diagram

4 结语

针对虚拟口腔正畸治疗系统中牙齿移动路径规划问题，本文提出了一种基于NSMPSO 算法的牙齿正畸路径规划方法。首先根据牙齿运动特性，将问题转化成带约束的多目标优化问题；其次，本文在简化粒子群算法的基础上，引入正态分布及均值粒子群的思想，提出了基于正态分布的简化均值粒子群算法（NSMPSO）；最后，构造了包含平移路径长度、旋转角度、碰撞检测以及牙齿在单阶段的移动量、旋转量的适应度函数，得到牙齿从开始位置到最终位置的最优路径解。在三大测试函数上进行对比实验，验证了提出的NSMPSO 算法与其他粒子群算法相比具有最高的收敛速度及最高的求解精度。同时在Matlab中进行仿真实验表明，利用该数学模型和改进算法求得的最优路径安全可靠，可以为医生辅助诊断提供有效的帮助，具有一定的实用价值。