具有拓扑时变和搜索扰动的混合粒子群优化算法

周文峰，梁晓磊*，唐可心，李章洪，符修文

（1.武汉科技大学汽车与交通工程学院，武汉 430065；2.上海海事大学物流科学与工程研究院，上海 201306）

（*通信作者电子邮箱liangxiaolei@wust.edu.cn）

0 引言

粒子群优化（Particle Swarm Optimization，PSO）算法是由Kennedy 和Eberhart［1-2］受鸟群等聚类生物寻觅食物行为的启发而提出的一种群体智能优化算法。PSO 算法具有原理简单、结构简洁、参数少和鲁棒性强等特点，在生产调度问题、车辆路径问题、神经网络优化和配送中心布局问题等领域得到广泛应用。和其他智能算法一样，在求解复杂高维度的函数时，PSO 算法容易出现早熟和陷入局部最优的现象。针对以上问题，国内外学者做了大量研究。张艺瀛等［3］提出了基于动态邻域的多策略进化的量子粒子群优化算法，定义了一种动态邻域选择机制和三个不同策略的局部吸引子更新方程。翟亚飞等［4］提出了改进PSO，根据需要求解的问题设计了编码和解码机制，并引进了变异机制和改进了传统的迭代机制。范厚明等［5］提出了混合粒子群算法，结合变邻域下降搜索为主体的适应性扰动机制，采用适应性选择邻域策略，并在邻域搜索中设置了可变的循环次数。刘宁庆等［6］提出了一种改进粒子群算法，对基本粒子群算法速度更新公式进行修改，设计了权重系数。刘明等［7］提出了一种基于定期竞争学习机制的多目标粒子群算法，将粒子群算法与竞争学习机制融合，提高了算法收敛性。张鑫等［8］等将二范数原理和差分算法中的交叉算子引入粒子群算法中，提出了一种含交叉项的混合二范数粒子群优化算法。Chang 等［9］提出了一种动态多种群粒子群算法，在进化过程中通过计算群距、群度和位置精度等一系列动态参数，将子群合并成更大的子群来加强个体之间的信息交流。Ghasemi 等［10］从数学中的向量理论出发，将向量模型与优化算法结合，提出了一种新的粒子群优化算法。Ebtehaj 等［11］提出了一种新的混合进化算法，将粒子群算法与自适应神经模糊推理系统相结合，对模糊隶属度函数值进行优化。

如何将粒子的拓扑结构进行时变和有效地改进迭代机制等问题，文献没有进一步的研究和讨论。本文从改变拓扑结构和改进粒子迭代机制的角度出发，提出了一种具有拓扑时变和搜索扰动的混合粒子群（Hybrid PSO with Topological time-varying and Search disturbance，HPSO-TS）算法，首先采用K-medoids 聚类算法对种群进行动态分割，形成多个簇，根据自身搜索到的解与邻域最好解进行比较，指导粒子搜索方向，这样不仅加强粒子间的信息交流，而且还提高粒子的搜索效率；然后在更新速度时引入非线性变化的极值扰动，增加粒子的多样性，帮助粒子跳出局部最优；最后通过引进全局搜索与局部搜索相互转换机制，并且在全局搜索中混合狮群算法和局部搜索中加入正弦扰动因子，不仅增加了粒子搜索方式的多样性和搜索的精度，平衡了全局搜索和局部搜索，还提高了算法跳出局部最优的能力。

1 粒子的拓扑结构时变策略和搜索扰动机制

1.1 粒子的拓扑结构时变策略

与社会群体“物以类聚”的思想类似，本文采用K-medoids聚类算法对种群进行动态分割，将具有相似特性的粒子聚集成一个簇。与倪庆剑等［12］研究多簇结构的可变拓扑策略中定期更换簇数量不同，本文中粒子的拓扑结构是随迭代次数的变化而变化的，每次种群完成位置更新后，将重新确定簇中心，再将种群进行划分。这样不仅使每个簇的粒子数不同，增加簇的多样性，还加强了簇间的信息交流。

K-medoids 算法是一种运用比较广泛的聚类方法，和K-means 算法相似。两者不同的是簇中心的选取，在K-means算法中，将中心点取为当前簇中所有个体的平均值，而在K-medoids 算法中，选取当前簇中的一个个体作为中心点，且要满足簇中其他所有点到这个个体的距离最短。粒子群的聚类过程如下：

步骤1 从种群N中随机选择K个粒子p1，p2，…，pk作为簇初始中心点。

步骤2 计算其余粒子到各个簇中心的距离dis(xj，pk)=，根据距离最小原则，将各个粒子划分到距离最近的簇内。

步骤3 对于每个簇，计算簇内所有粒子位置的均值，根据距离最小原则，选取离均值点最近的粒子作为簇中心。

步骤4 重复步骤2，判断是否达到终止条件，如果到达，停止迭代，输出结果；反之亦然。

1.2 粒子的搜索扰动机制

1.2.1 引入极值扰动

在粒子聚类成簇后，计算簇内所有粒子的适应度值，选择其中最优的粒子作为当前簇的最优值。为了加强簇之间的信息交流，本文将每个簇与其邻域内相邻两个簇建立合作联系。假设对于簇i，当前簇i搜索到的最优解为besti，比较与其相邻两簇的besti-1和besti+1，选择三者中最优的作为簇i的neibest。借鉴文献［13］，考虑到个体极值、全局极值和簇极值的影响，重新构建种群个体粒子的速度更新公式，如式（1）。并为了让粒子跳出局部最优，引入极值扰动因子d，调整粒子的个体极值和全局极值，使粒子有更多机会探索新的区域。采用非线性变化的扰动因子，前期扰动因子较大，粒子可以搜索更大的范围，后期扰动因子变小，有利于粒子的局部搜索。扰动因子更新公式，如式（2）。其中，为了平衡算法的全局搜索能力和局部改良能力，本文采用非线性的动态惯性权重系数公式，如式（3）：

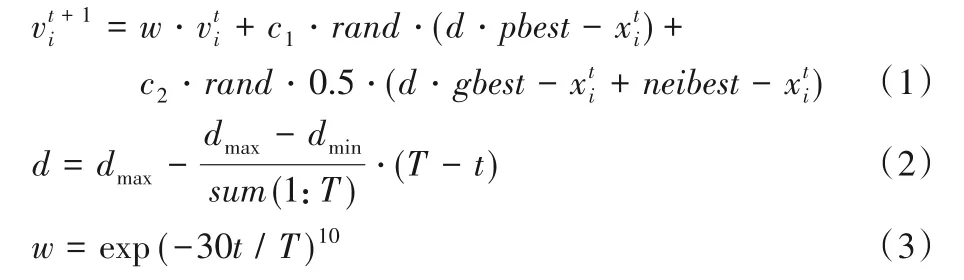
其中：c1、c2为学习因子；dmax为最大极值扰动因子；dmin为最小极值扰动因子；t为本次代数；T为最大迭代次数。

1.2.2 引入转换概率平衡搜索能力

在上述聚类过程完成以后，粒子将进行速度和位置的更新。为了平衡粒子的全局搜索和局部搜索，本文将引入花授粉算法（Flower Pollination Algorithm，FPA）［14］中转换机制，在基本花授粉算法中，模拟花粉异花授粉方式为全局搜索，模拟花粉自花授粉为局部搜索，两种搜索方式通过转换概率p控制，其中p∈[0，1]。转换概率对算法的性能影响较大，当转换概率p越小，粒子越容易进行局部搜索，则算法容易陷入局部最优；转换概率p越大，粒子越容易进行全局搜索，则算法的搜索精度不高。针对上述问题，本文采用线性变化的转换概率，让转换概率从最大值pmax线性递减到pmin，如式（4）：

根据实验数据可得，一般地，pmax取0.95，pmin取0.4时效果更好。

1.2.3 调整位置迭代公式

粒子在寻优的过程中，会根据转换概率进行全局搜索和局部寻优的转换。在全局搜索过程中，为了加强算法搜索能力，本文将对粒子的搜索策略进行修改，结合狮群算法［15］中母狮觅食的迭代机制的优点，从种群中随机挑选一个粒子协助当前粒子进行全局搜索，增加了粒子之间的信息交流，如式（5）。在局部搜索过程中，为了帮助算法跳出局部最优，本文引入了正弦扰动因子，如式（6）：

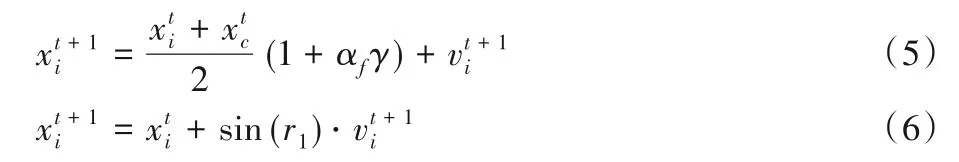
1.3 算法步骤

算法流程如图1所示。

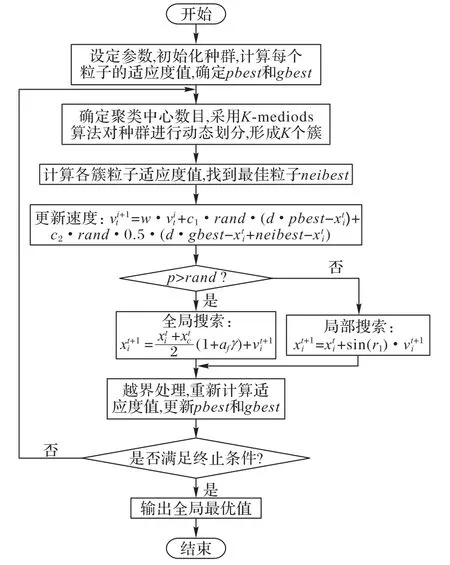
图1 算法流程Fig.1 Algorithm flowchart

算法具体实施步骤如下：

步骤1 初始化种群。在解空间，随机产生N个粒子的位置xi和速度vi(i=1，2，…，N)，计算每个粒子的适应度值。设定粒子速度的最大值Vmax和最小值Vmin，位置的最大值Xmax和最小值Xmin，学习因子c1、c2，维度D，最大极值扰动因子dmax，最小极值扰动因子dmin，最大迭代次数T，转换概率的最大值pmax和最小值pmin。

步骤2 随机选择K个粒子作为聚类中心，采用1.1 节中粒子的拓扑结构时变策略将种群分成K个簇。

步骤3 根据当前粒子的速度和位置，计算出每个粒子的适应值，得到个体历史最佳位置pbest、全局的最佳位置gbest和簇内最佳位置neibest，从而根据式（1）更新粒子的速度并进行越界处理。

步骤4 判断条件rand＜p，若满足条件则通过式（5）更新粒子的位置并进行越界处理；否则通过式（6）更新粒子位置并进行越界处理。重新计算粒子的适应度值，更新gbest和pbest。

步骤5 判断算法是否满足迭代的终止条件，若满足，则转至下一步，否则转至步骤2进行下一步迭代寻优。

步骤6 输出全局最优值，算法结束。

1.4 算法的复杂度分析

从算法流程来分析HPSO-TS 算法的时间复杂度，由单次种群搜索行为分析可知，种群初始化的时间复杂度为O（N·D）；计算所有粒子适应度值以及更新个体的pbest和全局粒子的gbest，其时间复杂度为O（N）；接下来采用K-medoids聚类算法对粒子群进行动态分簇，形成K个异构子群，以此便于子群内粒子间信息流通，其时间复杂度为O（N·K），由于K是常数且K≥1，所以O(N·K)=O(N)。在个体行为更新算法中，与基本PSO算法稍有不同，本文算法为了加强簇之间的信息交流，需要选择邻域中最优的作为neibest，其时间复杂度为O(||Le||+N·D)，||Le||表示邻域规模。因为上述步骤是按流程依次进行计算，所以HPSO-TS 算法的时间复杂度为max{O(N·D)，O(N)，O(N·D)，O(||Le||+N·D)}。由于D≥1，||Le||≥1 和K是常数，可知HPSO-TS 算法的时间复杂度为O(||Le||+N·D)。

可得结论，在固定迭代次数T下，HPSO-TS 算法的时间复杂度为O(T·(||Le||+N·D))。由于N·D＞＞||Le||，||Le||可忽略不计，因此本文算法的时间复杂度与基本PSO 算法的时间复杂度O(T·N·D)相近。

2 实验分析

2.1 测试函数

为了分析和比较算法的有效性，本文选择了花授粉算法FPA［14］、PSO［1-2］、改进粒子群（Improved PSO，IPSO）算法［4］、具有动态拓扑结构的粒子群（PSO with Topology，PSO-T）算法和本文的算法HPSO-TS 进行性能比较。8 个经典测试函数用于分别对以上5种算法进行实验测试。

1）Sphere函数。函数在xi=0时取得最小值0，为单峰函数。函数表达式见式（7）：

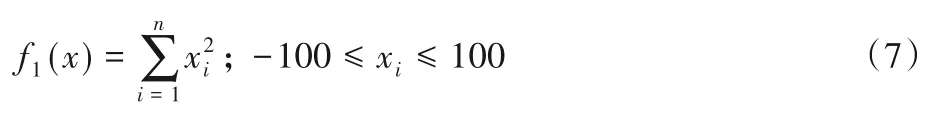
2）Quadric 函数。函数在xi=0时取得最小值0，为单峰函数。函数表达式见式（8）：

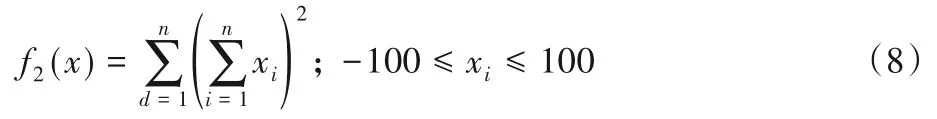
3）Griewank函数。函数在xi=0时取得最小值0，为多峰函数。函数表达式见式（9）：

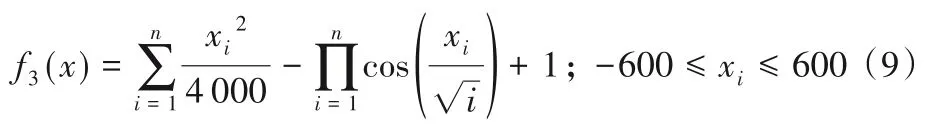
4）Ackley 函数。函数在xi=0时取得最小值0，为多峰函数。函数表达式见式（10）：

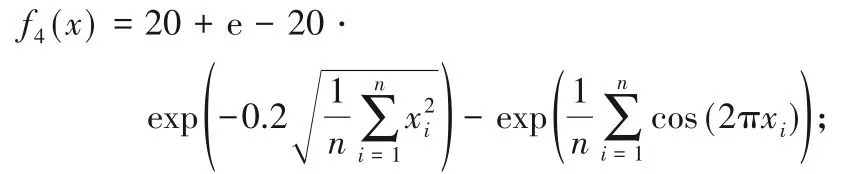
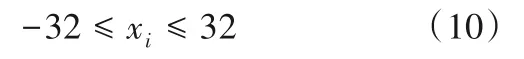
5）Rastrigin 函数。函数在xi=0时取得最小值0，为多峰函数。函数表达式见式（11）：

6）Step 函数。函数在xi=0时取得最小值0，为多峰函数。函数表达式见式（12）：

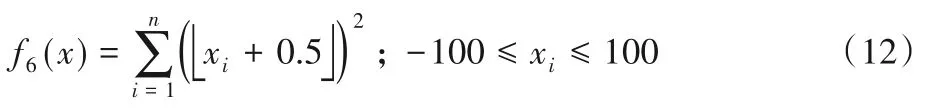
7）Sumsquares 函数。函数在xi=0时取得最小值0，为多峰函数。函数表达式见式（13）：

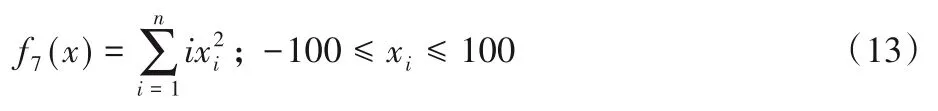
8）Tablet 函数。函数在xi=0时取得最小值0，为多峰函数。函数表达式见式（14）：

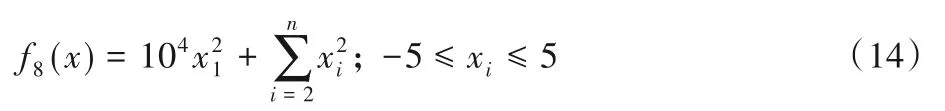
2.2 实验1：算法性能的统计学分析

PSO和IPSO中学习因子c1=c2=2.5，惯性权重采用线性递减方式wmax=0.95，wmin=0.4，此时两种算法有较好的性能。PSO-T和HPSO-TS中c1=c2=1，K=5。

为降低算法的随机性对实验结果的影响，以30 次独立运行实验的平均值作为评价算法性能的结果。表1 和表2 仅列举有代表性的函数在D=30 和D=50 上的最优值、最差值、平均值和方差。测试平台：Windows 7（64 位），Intel i5-4210U，2.40 GHz，4 GB RAM；在Matlab 2015b统一实现。

从实验数据来看，无论是D=30 还是D=50，对于大多数函数来说，HPSO-TS 算法搜索解的质量和稳定性都优于其他四种算法，这说明本文算法采用的聚类方式，有利于保持种群的多样性，使其不断搜索最优解；搜索解的精度也好于其他四种算法，这说明本文算法采用的搜索扰动机制，有利于保持种群的活性和粒子的多样性，使粒子搜索更多的区域，帮助粒子在迭代后期跳出局部最优，搜索精度更优的解。其中HPSO-TS 算法均可以搜到8 个函数的理论极值，同时搜索到解的质量和精度都好于其他四种算法。但是在D=30时，HPSO-TS 算法对于求解函数f4的稳定性提升有待提高，最优值可以达到理论极值0，而最差值只能到-15 数量级。函数f3是多峰函数，从函数图像可以看出此函数有很多峰值，本文算法求解时极易陷入局部最优；在D=50时，HPSO-TS算法均可以搜到所有函数的理论极值，求解表现较为优秀。

为了更好对比上述五种算法的寻优能力，图2、3 给出了有代表性函数的曲线收敛图，其他函数测试结果类似。为了便于观察，在不影响算法收敛特征下将纵坐标适应度值取以10为底的对数。结合表中数据和函数测试曲线，分析如下：

1）当D=30时，对于f4，HPSO-TS算法的求解精度要优于其他四种算法，但是依照测试曲线图的趋势，IPSO 算法收敛不明显。对于其他函数，HPSO-TS算法的求解质量、精度和鲁棒性都要明显强于另外四种算法。本文算法可以搜索到8 个函数的理论极值。其中从f6和f7测试曲线图可以看出，在算法迭代到300 次左右时，曲线下降很快，算法迅速收敛，这说明HPSO-TS算法引入搜索扰动机制，增加了粒子的活力，能有效地帮助粒子跳出局部最优，搜索到更优的解，进一步提高算法的求解能力。

2）当D=50时，在求解函数时，HPSO-TS 算法在求解精度、质量和算法稳定性方面都明显好于其他四种算法。尤其是本文算法可以搜索到所有函数理论极值。其中从函数f8曲线图可以看出，在算法迭代的次数1 000 以内时，曲线下降的速度很快，算法迅速收敛，这说明HPSO-TS 算法引入搜索扰动机制，增加了粒子的活力，有效地帮助粒子跳出局部最优，搜索到更优的解，进一步提高了算法的求解的能力。

综上所述，无论是对单峰还是多峰函数，HPSO-TS算法均可以获得高质量优化结果。与其他算法相比，本文算法具有更好的稳定性和搜索能力。该算法很好地缓解了早熟和收敛速度的矛盾，有效地平衡了全局搜索和局部搜索。

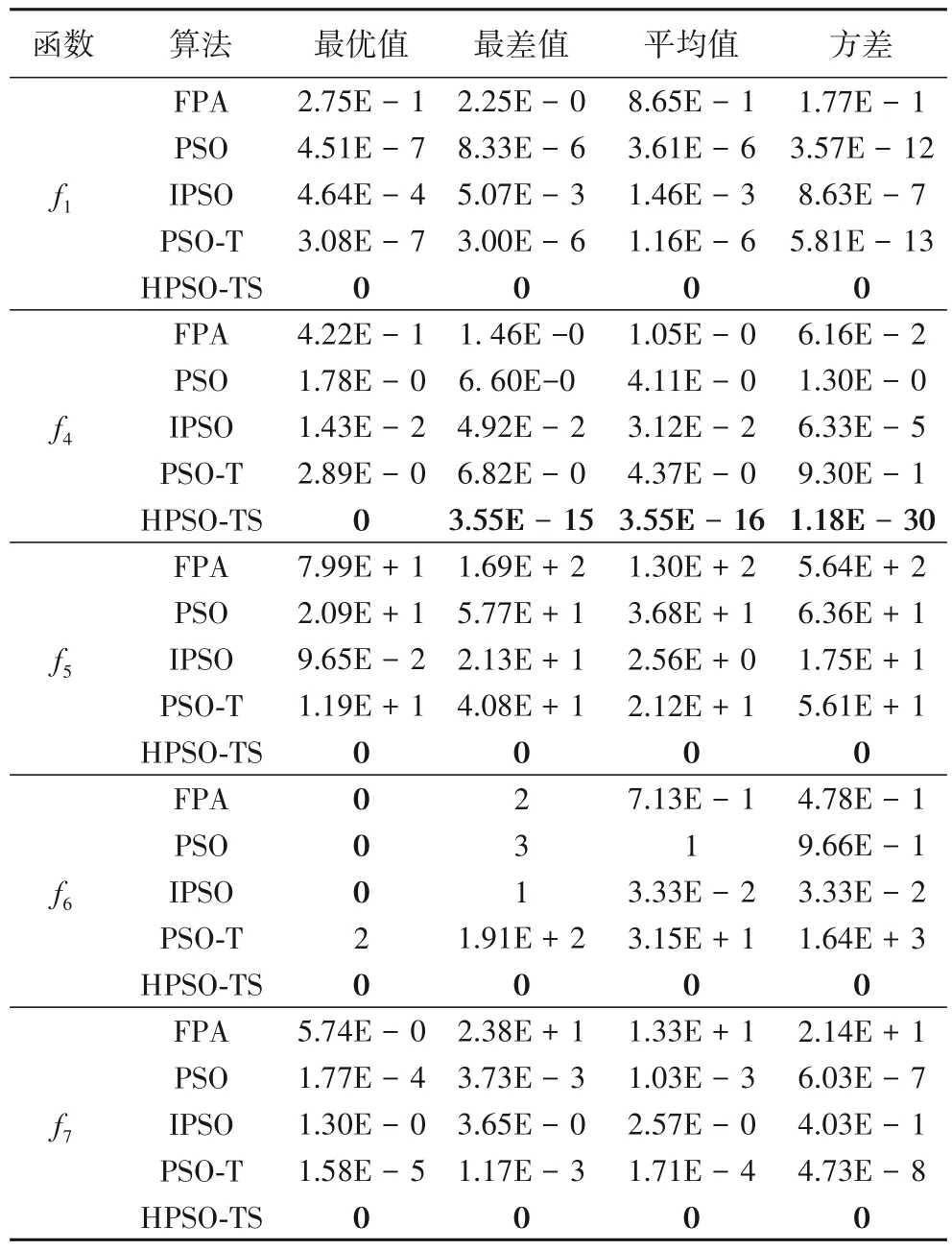
表1 函数测试实验结果（D=30）Tab.1 Experimental results of function tests（D=30）

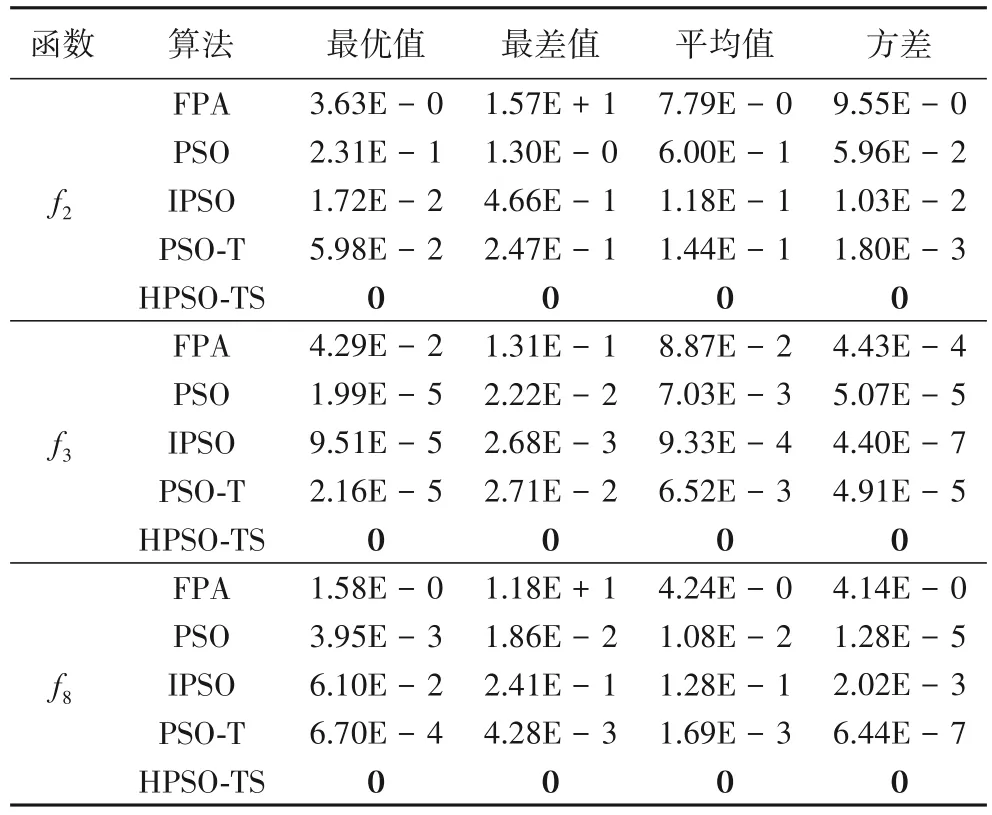
表2 函数测试实验结果（D=50）Tab.2 Experimental results of function tests（D=50）

2.3 HPSO-TS算法的收敛曲线特性分析

参照图2 和图3中6 个函数的算法收敛曲线，将本文HPSO-TS算法与FPA 算法、PSO 算法、IPSO 算法和PSO-T 算法比较，进行收敛性分析。

在f2和f6上，大部分算法能够求得较高精度的解，收敛曲线在1 000代内下降幅度明显，本文HPSO-TS算法收敛时所用的迭代次数更少，收敛曲线下降速度快，并且都能求得最优解。在f3上，其他四种算法收敛曲线图的趋势大体一致，曲线下降平缓，本文HPSO-TS算法在200代左右收敛，收敛速度较快，并可以求得函数的理论极值点。在f4上，五种算法都能求得较优的解，从收敛曲线图可以看出，本文算法收敛的速度和精度是最优的。在f7和f8上，从曲线图上可得其他四种算法收敛均较平缓，求得的函数解精度不高，本文HPSO-TS 算法收敛曲线下降速度快，能求得函数最优值。

以上分析说明HPSO-TS 算法采用的拓扑时变策略增加了种群的多样性，提高了算法的收敛性，有利于算法的全局搜索。引入的搜索扰动机制，增加了粒子的活力，有效地帮助粒子跳出局部最优，搜索更多可行解空间，从而求得更优的解，进一步提高了算法的求解的能力。

2.4 实验2：HPSO-TS算法对参数p的敏感性分析

在HPSO-TS 算法中，转换概率p是影响算法性能的重要参数，其作用是平衡个体的全局搜索和局部搜索。为了减少算法性能对p设置的敏感性，本文算法采用p值线性递减。实验中p分别取0.8、0.5、0.2 和线性变化（见式（4）），设置D=30，算法最大迭代次数T=4 000。实验结果如表3所示。

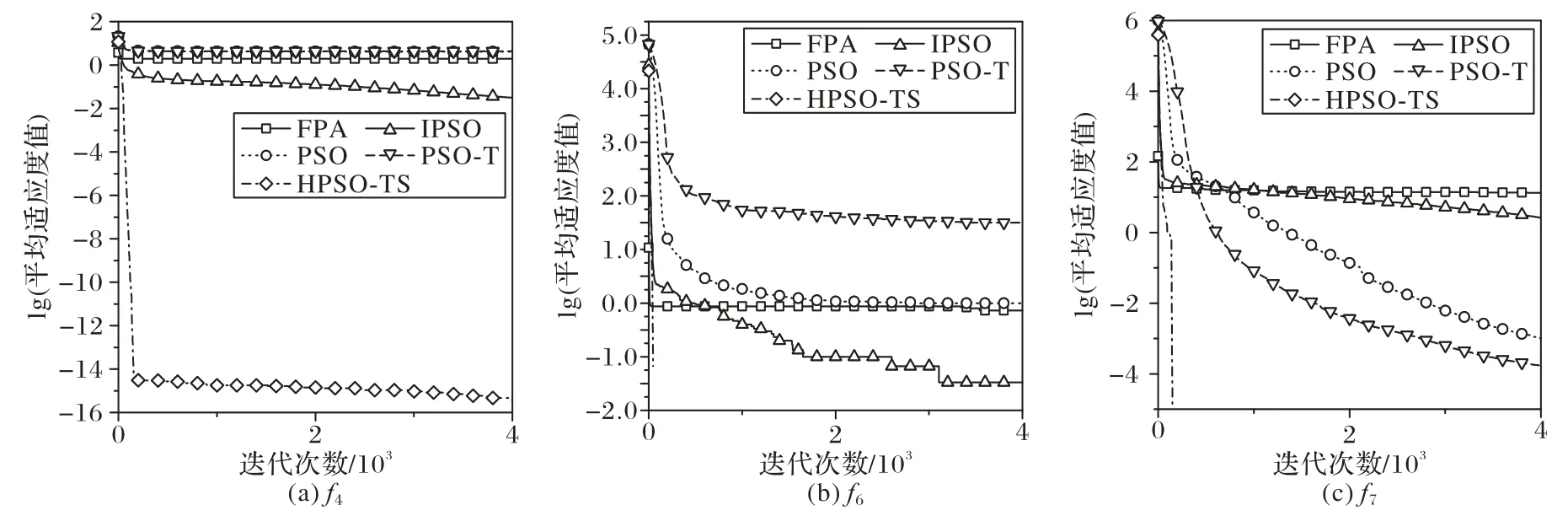
图2 三个函数测试曲线(D=30)Fig.2 Test curves of three functions (D=30)

图3 三个函数测试曲线(D=50)Fig.3 Test curves of three functions(D=50)

表3 不同p值的测试函数结果对比（D=30）Tab.3 Comparison of test function results with different p values(D=30)

从表3 可以看出，无论是对单峰函数还是对多峰函数，相同迭代次数时p值采用线性变化可以获得较好的结果。转换概率p对算法的性能影响较大：p越小，粒子越容易进行局部搜索，则算法容易陷入局部最优；p越大，粒子越容易进行全局搜索，则算法的搜索质量不高。当p=0.8时，算法求解精度不错，但求解质量不如采用线性变化的p值，这时p值较大，大部分粒子进行全局搜索，降低了算法的局部搜索能力；当p=0.5时，无论是在求解精度还是在求解质量方面，都不如采用线性变化的p值，这是由于p取0～1 的中间值，算法的全局搜索能力和局部搜索能力都没有达到较高水平；当p=0.2时，无论是在求解精度还是在求解质量方面，都不如采用线性变化的p值，这时p值较小，影响了算法的全局搜索能力，使得粒子无法在较优的局部进行搜索，算法的求解质量也受到影响。

综上所述，采用p值线性变化由大到小递减的HPSO-TS算法具有很好的稳定性和鲁棒性，开始阶段p值较大有利于粒子进行全局搜索，后期p值较小使得粒子加强局部搜素，寻得更优的解，这样全局搜索和局部搜索都能兼顾。

3 结语

本文针对基本PSO 算法容易早熟和陷入局部最优等问题，深入研究了种群粒子聚类思想和迭代机制，提出了一种基于拓扑结构的改进迭代机制的粒子群算法。在种群初始化时，采用K-medoids算法对种群进行聚类分簇，得到若干个簇，通过比较簇内粒子的适应度值得到邻域内最优的粒子来指导粒子进行迭代更新。然后考虑全局搜索和局部搜索调整，引入转换率平衡种群两种搜索行为，并融合狮群算法搜索策略，改进了迭代机制，重新更新粒子的位置，帮助粒子跳出局部最优。实验结果表明本文算法相比PSO 算法、FPA 具有更高的求解精度质量和更好的稳定性和鲁棒性，达到了预期效果。