双层规划的改进混合布谷鸟搜索量子行为粒子群优化算法

曾明华，全 轲

（华东交通大学交通运输与物流学院，南昌330013）（*通信作者电子邮箱296575845@qq.com）

0 引言

双层规划（Bi-Level Programming，BLP）是一类具有主从递阶关系结构的数学模型，它是将优化问题作为约束条件的极值问题［1］。该数学模型已广泛应用于资源分配、交通网络设计等实际问题。文献［2］证明了线性双层规划是NP-难问题。事实上，大多数双层规划还包括更复杂的非线性双层规划问题。求解双层规划的方法大致可分为传统算法和智能优化算法，但传统算法依赖于目标函数的可微性，不具有普遍的适用性。目前，对目标函数要求不高的智能优化算法已经广泛用于解决双层规划问题。

目前，已经有学者结合布谷鸟搜索（Cuckoo Search，CS）算法和粒子群优化（Particle Swarm Optimization，PSO）算法并用于求解一些实际应用问题。文献［3］将CS算法中的Lévy飞行和淘汰机制引入PSO算法中，形成混合优化算法。文献［4］将CS 算法引入动态多种群（Dynamic Multi-Swarm，DMS）-PSO算法，提高了原算法的全局搜索能力，提出DMS-PSO-CS 算法。文献［5］基于种群拓扑结构与粒子变异，同时加以CS 算法的偏好随机游走变异策略，提出基于拓扑结构与粒子变异改进的粒子群优化算法。文献［6］用CS算法中的Lévy飞行取代PSO 算法位置更新公式的随机数，提出一种PSO-CS 算法。文献［7］通过正交平方原理建立初始种群，动态调整CS 参数以最小化CS 的固定步长的影响，并将PSO 算法引入CS 算法中形成一种混合CSPSO 算法。文献［8］引入QPSO 算法用于CS 算法的位置寻优过程，以解决CS 算法在解决服务质量（Quality of Service，QoS）组播路由问题收敛速度慢、算法搜索效率低的问题。

根据以往的研究，混合CSPSO 算法相较于传统PSO 算法有更好的性能，但目前对QPSO 算法与CS 算法的混合算法研究较少，且尚未有学者将混合CSQPSO 算法用于求解双层规划。

本文结合量子行为粒子群优化算法、布谷鸟搜索算法以及模拟退火（Simulated Annealing，SA）算法以寻找双层规划问题最优解。对CS算法设计了一种改进动态步长Lévy飞行，并引入模拟退火算法中的Metropolis 准则，进而提出了一种改进混合布谷鸟搜索量子行为粒子群优化（Improved hybrid Cuckoo Search-based Quantum-behaved Particle Swarm Optimization，ICSQPSO）算法。该算法能有效增加粒子群多样性，增强粒子群跳出局部最优解的能力。对13 个复杂的双层规划的数值实验表明，所提出的算法非常有效，且大部分结果显著优于所参考的四种改进粒子群算法和一种改进遗传算法。

1 双层规划问题描述

双层规划数学模型一般可以表述如式（1）：

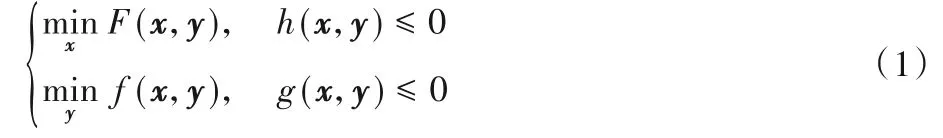
其中：x为上层决策变量，y为下层决策变量，，；X是设定了对上层决策变量的额外限制，例如上下界 。，R是实数集。

对于双层规划模型给出如下基本概念［9］。

1）约束区域：S={(x，y)|h(x，y) ≤0，g(x，y) ≤0}。

2）对于给定的x∈X，下层规划可行域为：

S(x)={y|g(x，y) ≤0}

3）S在上层决策空间的投影为：S(X)={x|∃y，(x，y)∈S}。

4）对于每个x∈S(X)，下层合理反应集为：

Q(x)={y|y∈arg min{f(x，y)，y∈S(x)}}

5）诱导域：IR={(x，y)|(x，y)∈S，y∈Q(x)}。

进一步给出双层规划模型可行解和最优解的概念：若点(x，y)∈IR，则称点(x，y)为双层规划模型的可行解。若点(x*，y*)是双层规划模型的可行解，且对任意(x，y)∈IR有F(x*，y*)≤F(x，y)，则称(x*，y*)为双层规划模型的最优解。

2 求解双层规划问题的ICSQPSO算法

2.1 标准算法

2.1.1 标准QPSO算法

PSO 算法是由Kennedy 等［10］在1995年提出的一种智能优化算法，具有实现容易、收敛快等优点；但是原始PSO 算法在优化后期由于种群在搜索空间中多样性的丢失容易早熟收敛，陷入局部最优解。文献［11］提出了一种量子行为粒子群优化算法。在QPSO 算法中，由概率密度函数描述的束缚状态的粒子可以以一定概率出现在整个可行搜索空间的任何区域，具有全局收敛性。

假设算法搜索区域的维度是D，粒子群粒子数目是N。代表第i个粒子在j维空间中的位置。pi=代表第i个粒子在j维空间中当前搜索到的最优位置，代表整个粒子群在j维空间中当前搜索到的最优位置，i=1，2，…，N，j=1，2，…，D。相较PSO 算法的粒子位置和速度更新模型，QPSO算法仅采用粒子位置更新模型，如式（2）～（6）所示：

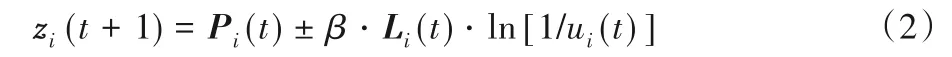
其中：

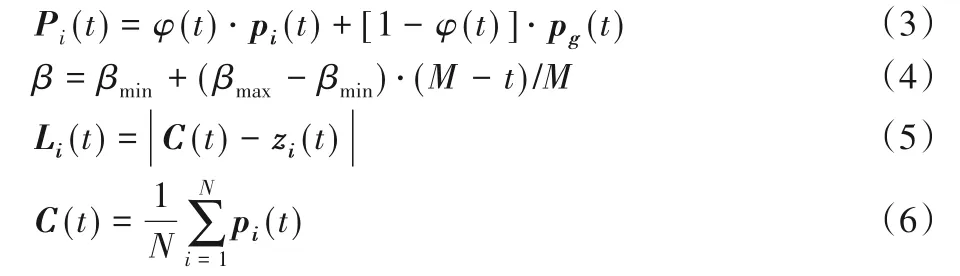
其中：Pi(t)称为吸引子，这个点在迭代过程中会不断吸引粒子靠近，φ(t)和ui(t)是［0，1］上均匀分布的随机数；β称为收缩—扩张系数，用于协调迭代过程中粒子全局和局部的搜索性能，常采用线性减小的方式，如式（4），M是最大迭代次数；t是当前迭代次数；Li(t)表示当前粒子位置与平均个体最好位置C(t)距离的绝对值。

2.1.2 标准CS算法

CS 算法是一种新兴智能算法，由Yang 等［12］于2009 年提出，其主要思想是模拟布谷鸟借巢产卵的习性，利用鸟类的Lévy 飞行机制，通过偏好随机游走搜索到最优的鸟巢以孵化鸟蛋。该算法的优点是不易陷入局部最优且全局搜索能力强，但收敛速度较慢。文献［12］假设了CS 算法中的3 种理想状态：

1）每次布谷鸟只生产一枚卵，并随机选择一个鸟窝孵化；

2）在搜索鸟窝的过程中，保留拥有最高质量卵的鸟窝到下一代；

3）每一代的鸟窝数量固定，鸟窝中的卵被宿主发现的概率是p。

基于上述第3个假设，CS算法通过式（7）将搜索的位置和路径更新：

其中：zi(t)代表第i个鸟窝在第j维空间中第t代时的位置；α为步长缩放因子，通常α为固定值，取值为0.01；⊕为点对点乘法；L(λ)为Lévy飞行的随机搜索路径。

针对第三个假设，利用偏好随机游走机制生成新解，即用随机数r∈[0，1]与p对比，若r＞p，则对zi按式（8）进行随机改变，反之不变：

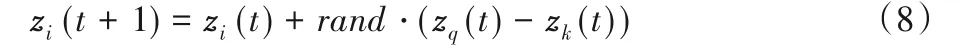
其中：rand为[0，1]区间的随机数；zq(t)和zk(t)是种群中随机选取的两个不同个体。文献［13］已详细介绍CS算法，本文不再赘述。

2.1.3 标准SA算法

模拟退火（SA）的思想起源于固体的退火过程，最早由Metropolis 于1953 年提出［14］。当SA 算法用于最优化问题时，首先要设定一个初始温度TS、终止温度Tf以及温度衰减系数ς。温度衰减函数采用常用线性函数，如式（9）：

其中T(t)为某时刻t的温度。

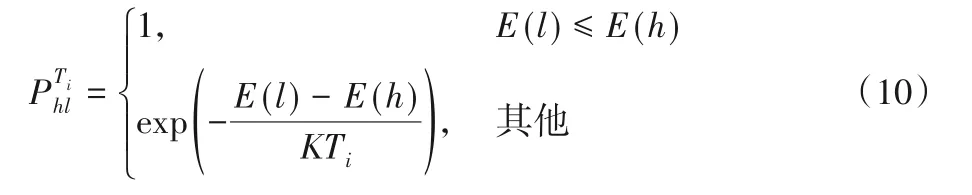
在退火过程中温度为T(t)的时刻，固体从状态h转变到另一个状态l遵循如式（10）所示的Metropolis准则：其中：K为波尔兹曼常数；E(l)和E(h)分别为在状态l和h下固体的内能，在最优化问题中，固体的内能可以看作是目标函数值。在Metropolis 准则下，SA 算法一定能接受最优解，同时也能以一定概率接受较差解。正因为有这种机制，SA 算法不易陷入局部最优解。

2.2 改进的Lévy飞行

式（7）中的步长缩放因子α是一个重要参数，在原始CS算法中，α是固定常数，可能会影响算法的收敛速度［15］。为了提高收敛速度，本文提出一种如式（11）所示的分段函数以动态调整α，α随着迭代次数的增加而减小。这与PSO 算法中随着迭代次数增加而惯性权重减小的原理类似。在迭代初期，α足够大以促使CS 算法搜索到更多可行解，保证了解的多样性；在迭代末期，α较小，更好地微调可行解向最优解靠拢。

其中：αmax和αmin分别是α的最大值和最小值。

2.3 约束条件处理

本文假设上层和下层函数分别存在m个不等式约束，采用罚函数法处理式（1）的约束条件。以下层规划函数为例，可以根据式（12）计算粒子的适应度fitness(x，y)：

其中：S为足够大的正常数，称为惩罚因子。

2.4 ICSQPSO算法步骤

ICSQPSO 算法流程如图1 所示，其详细步骤包括上层规划模型的求解算法（算法1）和下层规划模型的求解算法（算法2）。算法1与算法2分别描述如下。

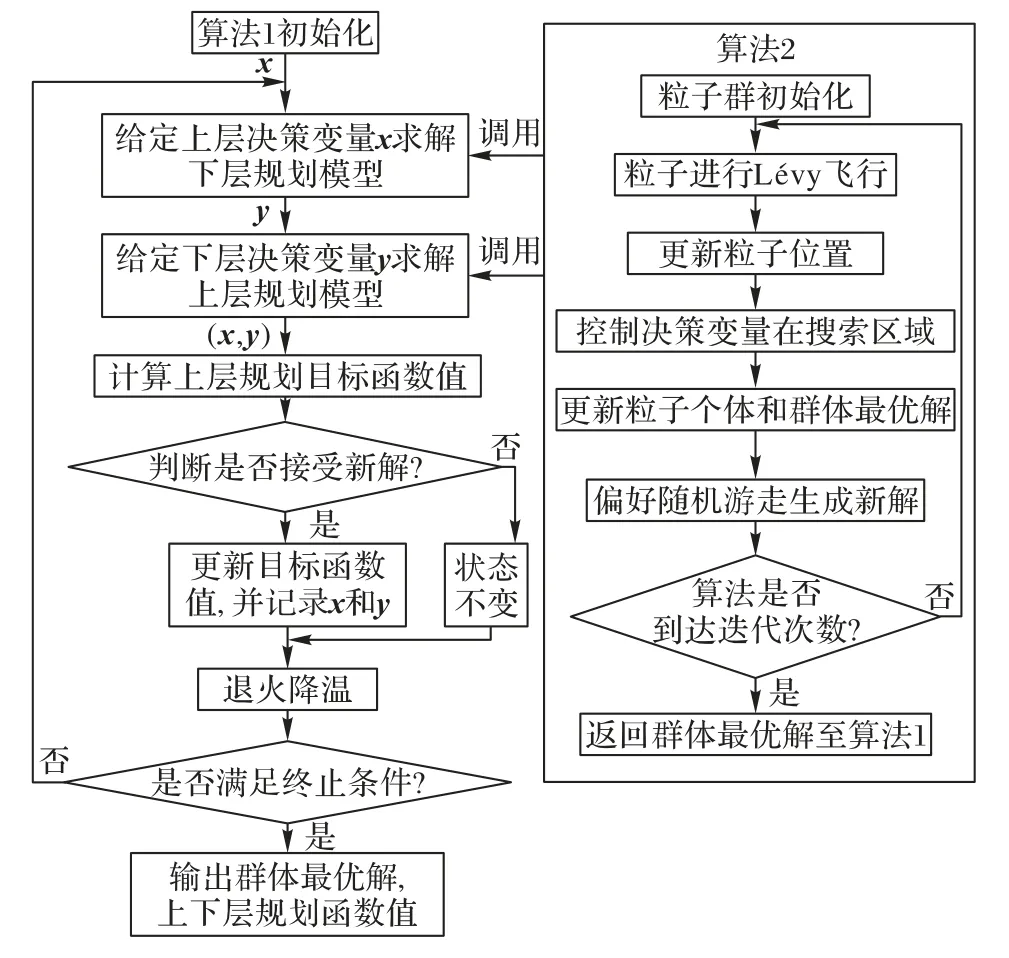
图1 ICSQPSO算法流程Fig.1 Flowchart of ICSQPSO algorithm

算法1 上层规划模型的求解算法。

1）初始化参数：最大迭代次数M1，迭代次数t1=0，初始温度TS、终止温度Tf以及温度衰减系数ς。

2）将上层规划模型的解x*j(t1)（j=1，2，…，n1）代入下层规划模型，调用算法2求得下层规划模型的最优解y*w(t1)（w=1，2，…，n2）。

3）将y*w(t1)代入上层规划模型，调用算法2 求得上层规划模型的最优解x*j(t1)。

4）将x*j(t1)与y*w(t1)代入上层规划的目标函数，计算目标函数值，按式（10）进行Metropolis 准则判断，若接受，则记为Fbest。

5）按式（9）进行退火降温。置t1←t1+1。

6）若t1≥M1，T(t1)≤Tf，则转至7）；否则，返回2）。

7）结束计算。输出群体最优解(x*j(t1)，y*w(t1))以及上层规划和下层规划的目标函数值。

算法2 下层规划模型的求解算法。

1）初始化参数：粒子群数目N，收缩-扩张系数βmax和βmin，步长缩放因子上下限αmax和αmin，最大迭代次数M2，迭代次数t2=0，惩罚因子S，发现概率p，每个决策变量的上下界；随机初始化粒子群中粒子的位置zi(t2)；将第i个粒子的pi设为该粒子的当前位置，并计算各个粒子的适应度，设pg为初始粒子群中最佳粒子的位置。

2）粒子按式（7）进行Lévy 飞行，并利用式（2）更新粒子的位置。

3）检查更新完后的zi(t2)中各个决策变量大小是否超过上界或低于下界。若超过上界，则将其控制在上界边界处；若低于下界，则将其控制在下界边界处。

4）更新个体最优解pi和群体最优解pg。如果粒子i的适应度优于其pi的适应度，则该粒子的pi更新为当前位置zi(t2)；如果粒子i的适应度优于当前pg的适应度，则pg更新为当前位置zi(t2)。

5）在一定概率p的条件下，利用式（8）对zi(t2)进行随机更新。置t2←t2+1。

6）若t2≥M2，则返回群体最优解pg至算法1；否则，返回2）。

3 算例和算法性能分析

本文选取了13 个算例来验证ICSQPSO 算法的有效性。算例既包括线性双层规划，也包括高度非线性双层规划，还有分式规划以及含有多个下层规划的双层规划。其中算例1～4选自文献［15］的例1、例2、例5、例8，算例5～7 选自文献［16］的例7～9，算例8 选自文献［17］的例11，算例9 选自文献［18］的例2，算例10～13选自文献［19］的例1～4。

ICSQPSO 算法参数设置：粒子群数目N=40，初始温度TS=10 000，终止温度Tf=0.36，温度衰减系数ς=0.95，收缩-扩张系数最大值βmax=1，最小值βmin=0.5，步长缩放因子最大值αmax=0.5，最小值αmin=0.01，最大迭代次数M1=200，M2=300，经过数值实验测试选定ta=150，惩罚因子S=100 000，发现概率p=0.25。图2 给出了算例1 的上层规划目标函数值的演进过程，可以看出，ICSQPSO 算法在求解过程中快速收敛，算法在其他算例中也表现出相同的效果。

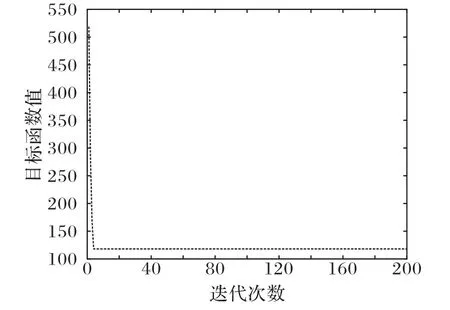
图2 算例1目标函数值的变化过程Fig.2 Changing process of objective function value of example 1

每个算例单独运行30次，记录30次运行中的上层规划函数F(x，y)最优值Fbest、下层规划函数f(x，y)最优值fbest、以及上下层规划函数最优值对应的最优解(x*，y*)。Fbest、fbest的 结果如表1 所 示，(x*，y*) 的 结果如表2 所 示，并 按(Fbest文献-Fbest本文)/Fbest文献计算了ICSQPSO 算法相比文献［15-19］算法所得Fbest的减少（优化）程度，计算结果如表1倒数第二列所示；同时，按相似方法计算比较了ICSQPSO 算法与文献［15-19］的比较文献算法的Fbest的减少（优化）程度，如表1 最后一列所示。这里，所谓文献［15-19］的比较文献算法，是指文献［15-19］用来与其所提出算法进行计算结果比较的算法。

本文将ICSQPSO 算法的测试结果与文献［15-19］算法进行对比。用于对比的算法有：文献［15］提出的PSO-CST（Particle Swarm Optimization with Chaos Searching Technique）算法；文献［16］提出的IBPSO（Improved Bilevel Particle Swarm Optimization）算法；文 献［17］提出的HPSOBLP（Bi-Level Programming based on Hierarchical Particle Swarm Optimization）算法；文献［18］提出的IPSO-BLPP（Bi-Level Programming Problem based on Improved Particle Swarm Optimization）算法；文献［19］提出的一种基于新编码方式的改进遗传算法。

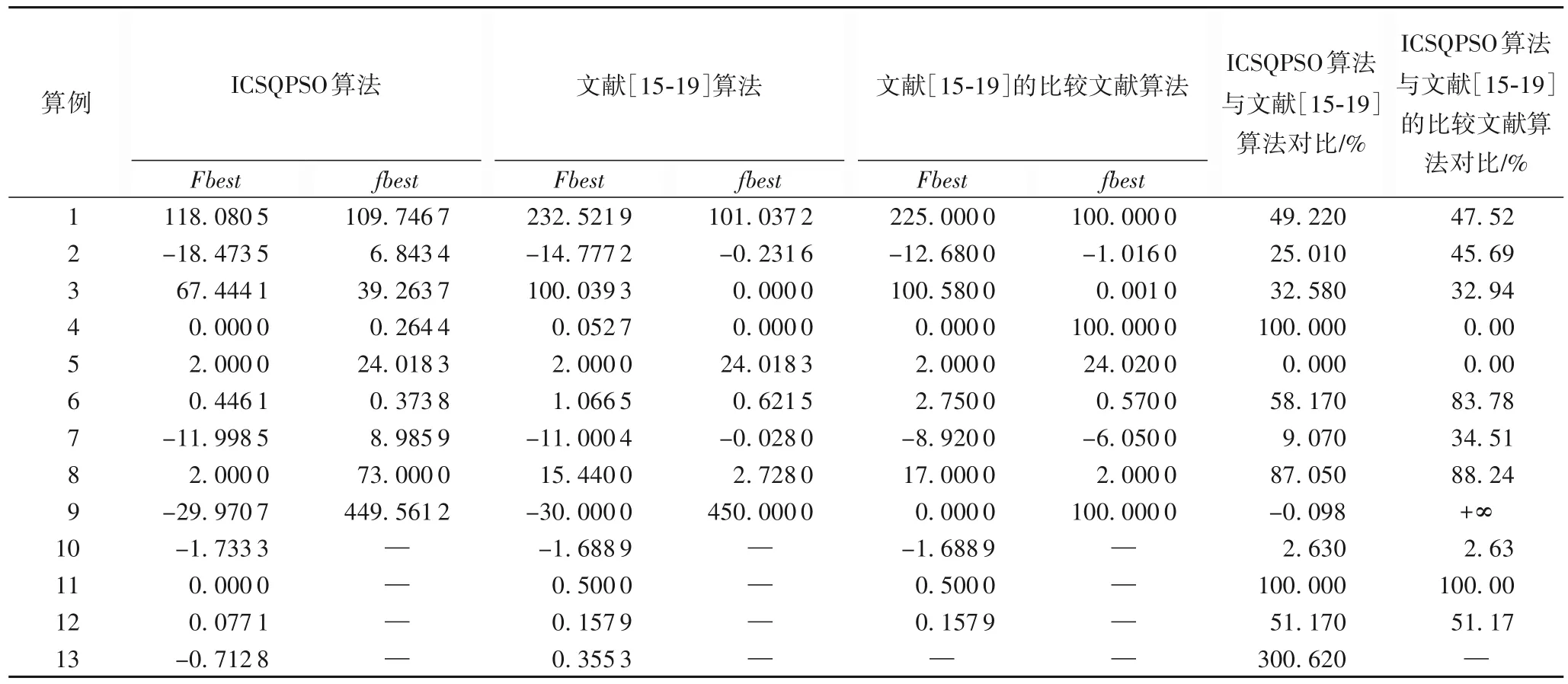
表1 目标函数最优值对比Tab.1 Comparison of objective function optimal value

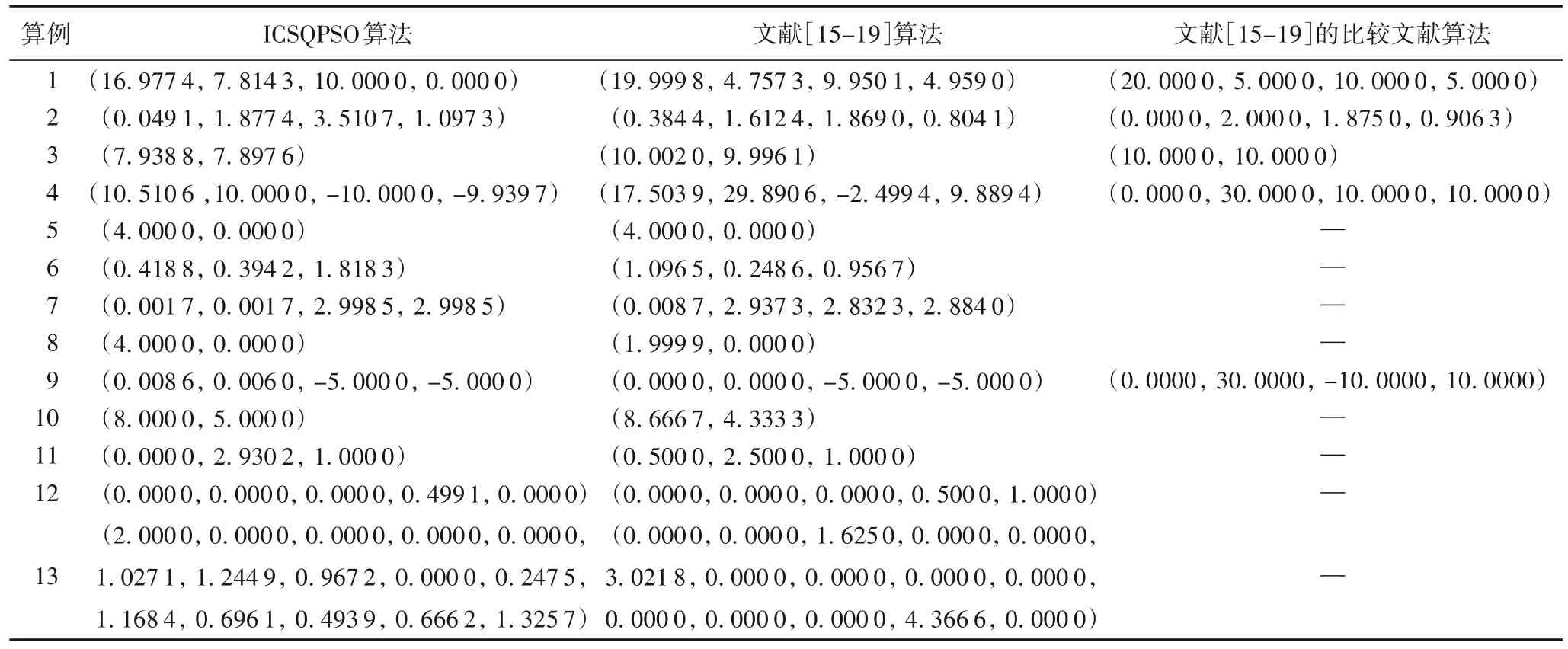
表2 不同算法之间决策变量最优解对比Tab.2 Comparison of optimal solutions of decision variables among different algorithms

从表1 和表2 可以看出，除了算例5 和9，本文提出的ICSQPSO 算法的计算结果均优于文献［15-19］的计算结果。其中对于复杂的非线性双层规划算例1，ICSQPSO 算法发现了一个优秀的解（16.977 4，7.814 3，10.000 0，0.000 0），其对应的上层规划目标函数最优值Fbest=118.080 5，较文献［15］的Fbest=232.521 9大幅减小了49.22%；对于高度非线性双层规划算例6，ICSQPSO 算法求得了一个出色的解（0.418 8，0.394 2，1.818 3），其上层规划目标函数最优值Fbest=0.446 1，较文献［16］的Fbest=1.066 5 减小了58.17%；对于包含多个下层规划的高维非线性双层规划算例13，ICSQPSO 算法能求解出比文献［19］的改进遗传算法更好的解，ICSQPSO算法求得Fbest=-0.712 8，而文献［19］求得Fbest=0.355 3，这表明本文算法在求解多下层分式双层规划时表现良好。

综上所述，对于大多数算例，本文提出的ICSQPSO 算法能找到比文献［15-19］算法更好的解，能有效地求解线性双层规划、单下层分式线性双层规划、多下层线性双层规划以及复杂的非线性双层规划。

4 结语

针对PSO 算法求解双层规划容易陷入局部最优解的问题，从增加粒子群多样性、增强粒子群跳出局部最优解的能力的角度出发，基于SA 算法中的Metropolis 准则，并将改进CS算法的动态步长Lévy 飞行和偏好随机游走机制嵌入QPSO 算法中，提出了一种ICSQPSO 算法。该算法具有保持种群多样性与提高全局搜索能力的优点：一方面，采用QPSO 算法代替PSO 算法，并引入Metropolis 准则，在求解过程中既能接受好解也能以一定的概率接受坏解，增强全局寻优能力；另一方面，改进CS算法中的动态步长Lévy飞行能使粒子群在优化中保持较高的多样性，保证搜索广度，偏好随机游走机制帮助粒子跳出局部最优解。对13 个具有典型代表性的算例进行数值实验，结果表明，所提出的ICSQPSO 算法能得到显著优于文献［15-19］算法的结果，对求解双层规划模型是非常有效的。