高二数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分.)

1.在(1+x)8的展开式中，含x2项的系数为( )

(A)28 (B)56 (C)70 (D)8

2.设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则(x,y)满足( )

(A)(x+1)2+y2=1

(B)(x-1)2+y2=1

(C)x2+(y-1)2=1

(D)x2+(y+1)2=1

3.一袋中装5只球,编号为1,2,3,4,5,在袋中同时取出3只,以ξ表示取出的三只球中的最小号码,则随机变量ξ的取值是( )

(A) 0,1,2,3 (B)1,2,3,4

(C) 1,2,3 (D) 1,2,3,4,5

4.函数y=2sinxcosx的导数为( )

(A)y′=cosx

(B)y′=2cos 2x

(C)y′=2(sin2x-cos2x)

(D)y′=-sin 2x

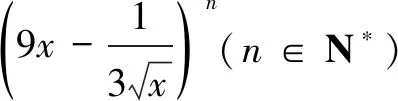
(A) 84 (B)-252 (C) 252 (D)-84

6.已知函数y=x2-x在x=2处的切线为l,则直线l与两坐标轴围成的三角形面积为( )

7.在(2x-3y)10的展开式中,奇数项的二项式系数和与各项系数的和的比值为( )

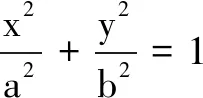
(A) 43 (B) 72 (C) 863 (D) 90

二、多项选择题(本题共4小题,每小题5分,计20分)

9.下列命题错误的是( )

(A)(-i)2=-1

(B)-i2=-1

(C)若a>b,则a+i>b+i

(D)若z∈C,则z2>0

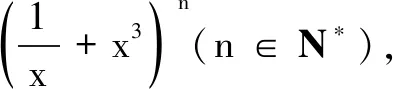
(A)存在n∈N*，展开式中有常数项

(B)对任意n∈N*，展开式中没有常数项

(C)对任意n∈N*，展开式中没有x的一次项

(D)存在n∈N*，展开式中有x的一次项

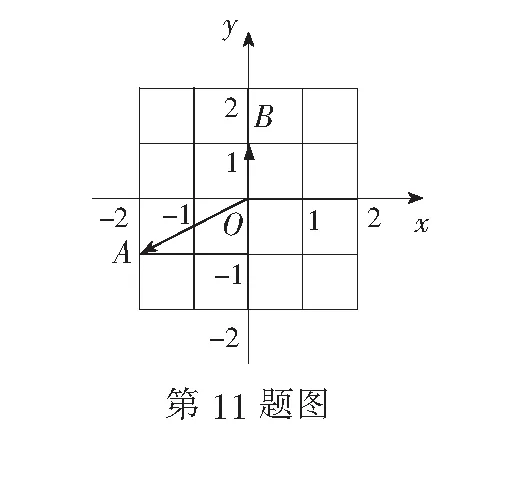
11.下列结论正确的是( )

(A)“z1,z2互为共轭复数”是“|z1|=|z2|”的充分不必要条件

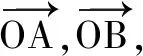
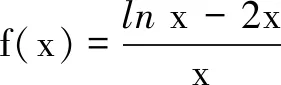
12.关于函数f(x)=sin|x|+|sinx|有下述四个结论,其中所有正确的结论是( )

(A)f(x)是偶函数

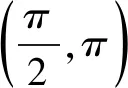
(C)f(x)在[-π,π]有4个零点

(D)f(x)的最大值为2

三、填空题(本题共4小题,每小题5分,计20分)

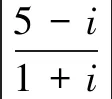
14.0,1,3,4四个数可组成______个无重复数字的不同的四位数(以数字作答).

15.已知函数f(x)=lnx+a(1-x),当f(x)有最大值，且最大值大于2a-2时，则a的取值范围是______.

四、解答题(本大题共6小题，计70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知i是虚数单位，复数z=2-i+(4-2i)i.

(1)求复数z的模|z|;

(2)若z+mz+n=1+3i(m,n∈R,z是z的共轭复数)，求m和n的值.

18.(本小题满分12分)(1)若离散型随机变量X的分布表为

X01P9c2-c3-8c

试求出常数c;

(2)一个袋子中有3个新球和7个相球，逐个从袋中取球，直到取到旧球时停止，记X为取球的次数，设袋中每个球被取到的可能性相同，每次取出的球都不放回袋中，求出X的分布.

19.(本小题满分12分)已知函数f(x)=ax3+bx2+x+1,当x=1时，函数f(x)有极值1.

(1)求函数f(x)的解析式；

(2)若关于x的方程f(x)-m=0有一个实数根，求实数m的取值范围.

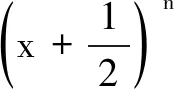
(1)求n的值；

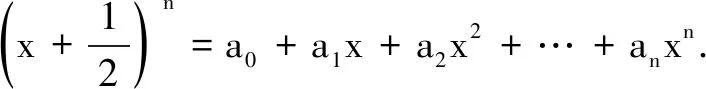
(i)求a5的值；

(ii)求a0-a1+a2-a3+…+(-1)nan的值;

(iii)求ai(i=0,1,2,…,n)的最大值.

21.(本小题满分12分)如图,以两条互相垂直的公路所在直线分别为x轴、y轴建立平面直角坐标系.

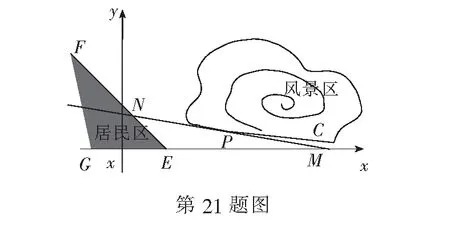
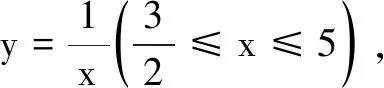
(1)设点P的横坐标为t,写出∆EMN面积的函数表达式S(t);

(2)当t为何值时,∆EMN面积最小?并求出最小面积.

22.(本小题满分12分)若函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数，试讨论

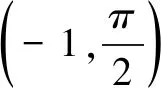
(2)f(x)的零点个数.

参考答案

一、单项题

1.A；2.C;3.C;4.B;5.A;

6.C;7.B;8.B.

二、多项选择题

9.BCD；10.AD;11.ABD;12.AD.

三、填空题

16.-20 160.

四、解答题

17.z=2-i+4i+2=4+2i,则

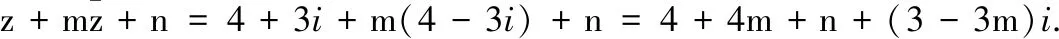
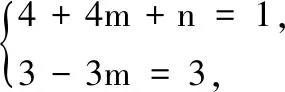
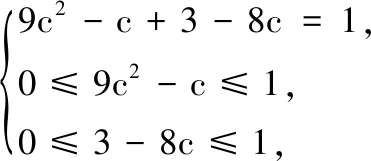
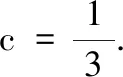
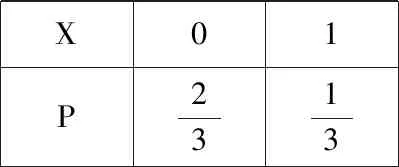
X01P2313

(2)随机变量X的可能取值为1，2，3,4.

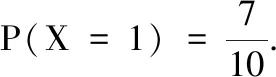
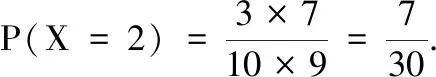
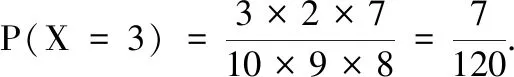
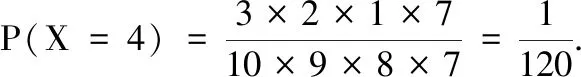
故X的分布表为

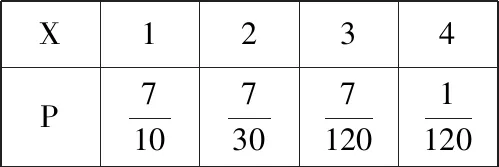
X1234P71073071201120

19.(1)由f′(x)=3ax2+2bx+1,得f′(1)=3a+2b+1=0;又f(1)=a+b+2=1,解得a=1,b=-2.

故f(x)=x3-2x2+x+1.

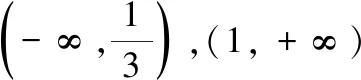
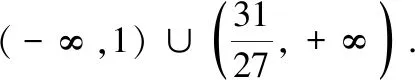
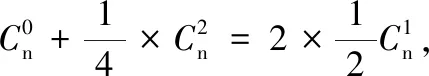
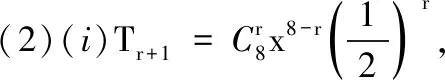
(iii)设第r+1项的系数为最大，则有

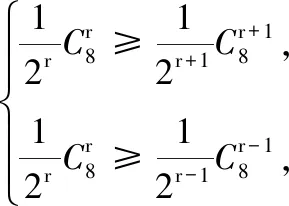
解得r=2或r=3.所以a1系数最大值为7.

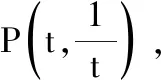
又E(1,0),∠OEF=45°，故直线EF的方程为y=-x+1.

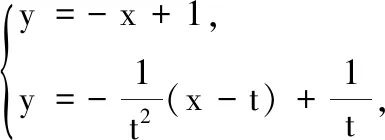
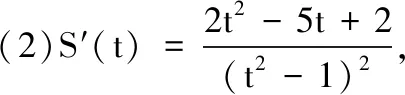
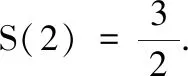
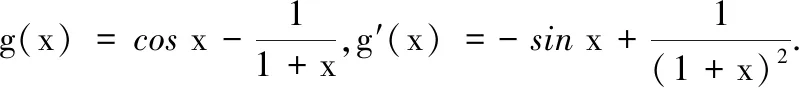
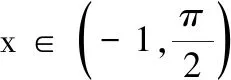
(2)f(x)的定义域为(-1,+∞).

(i)当x∈(-1,0]时，由(1)可知f′(x)在(-1,0)单调增，而f′(0)=0,故x∈(-1,0)时，f′(x)<0,f(x)单调减.又f(0)=0,从而x=0是f(x)在(-1,0]的唯一零点.

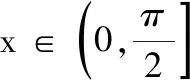
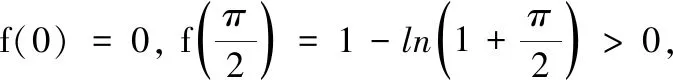
(iv)当x∈(π,+∞)时，ln(x+1)>1,所以f(x)<0,从而f(x)在(π,+∞)没有零点.

综上，f(x)有且仅有2个零点.