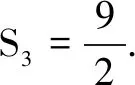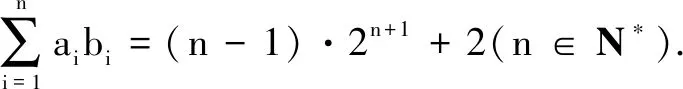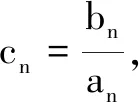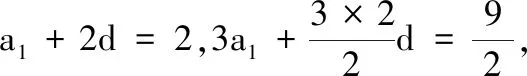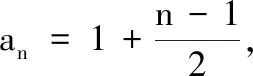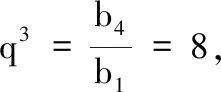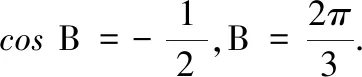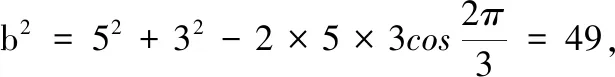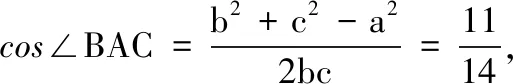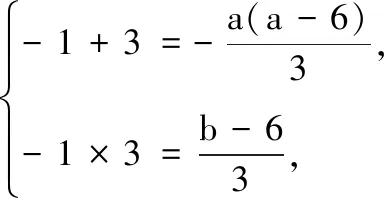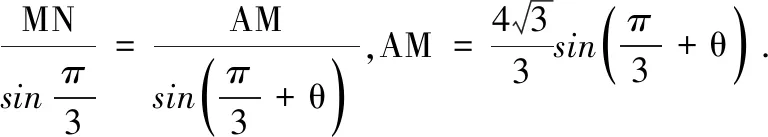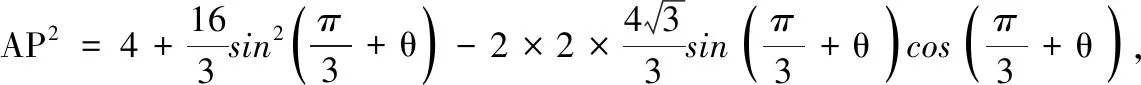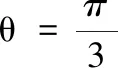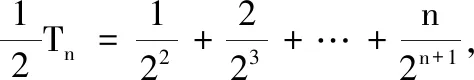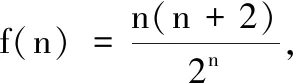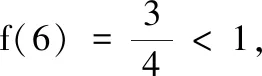高一数学测试
一、选择题(本大题共12小题,每小题5分,计60分)
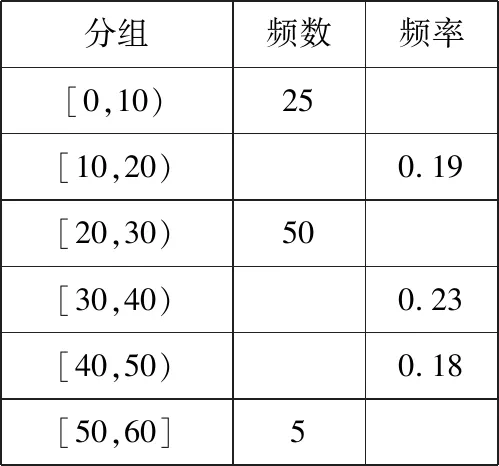
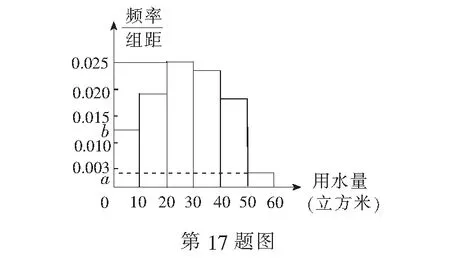
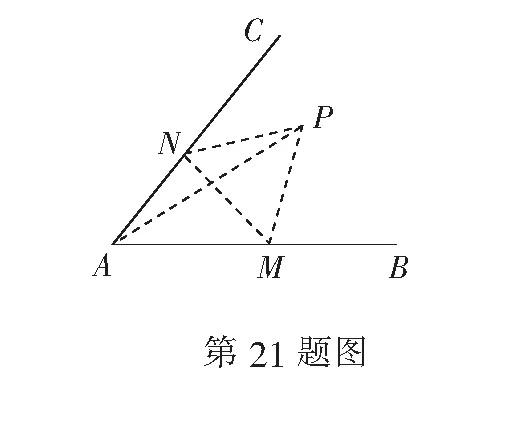
1.已知集合M={x|-4 (A){x|-4 (B){x|-4 (C){x|-2 (D){x|2 3.记Sn为等差数列{an}前n项和.已知S4=0,a5=5,则( ) (A)an=2n-5 (B)an=3n-10 4.已知一组数据6,7,8,8,9,10,则该组数据的方差是( ) 5.在∆ABC中,若sinA∶sinB∶sinC=3∶5∶7,则角C等于( ) (A)30° (B)60° (C)120° (D)150° 7.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) (A)1盏 (B)3盏 (C)5盏 (D)9盏 9.若不等式x2-2ax+a>0对一切实数x∈R恒成立,则关于t的不等式at2+2t-3<1的解集为( ) (A)(-3,1) (B)(-∞,-3)∪(1,+∞) (C)∅ (D)(0,1) 12.已知关于x的不等式x2-6x+a≤0的解集中有且仅有3个整数,则所有符合条件的整数a的值之和是( ) (A)13 (B)18 (C)21 (D)26 13.有A,B,C三所学校,学生人数的比例为 3∶4∶5, 现用分层抽样的方法招募n名志愿者,若在A学校恰好选出 9 名志愿者,那么n=______. 15.设Sn为数列{an}的前n项和,且a1=4,an+1=Sn,n∈N*,则a5=______. 17.(本小题满分10分)我们知道,地球上的水资源有限,爱护地球、节约用水是我们每个人的义务和责任.某市政府为了对自来水的使用进行科学管理,节约水资源,计划确定一个家庭年用水量的标准,为此,对全市家庭日常用水的情况进行抽样调查,并获得了n个家庭某年的用水量(单位:立方米),统计结果如下表所示. 分组频数频率[0,10)25[10,20)0.19[20,30)50[30,40)0.23[40,50)0.18[50,60]5 (1)分别求出n,a,b的值(a,b在频率分布直方图中); (2)若以各组区间的中点值代表该组的取值,试估计全市家庭平均用水量. (1)求数列{an}的通项公式; (2)设等比数列{bn}满足b1=a1,b4=a15,求数列{bn}的前n项和Tn. 19.(本小题满分12分)已知∆ABC的内角A,B,C的对边分别为a,b,c,且满足2c+a=2bcosA. (1)求角B的大小; (2)若a=5,c=3,边AC的中点为D,求BD的长. 20.(本小题满分12分)已知f(x)=-3x2+a(6-a)x+6. (1)若f(1)>-4,求实数a的取值范围; (2)若不等式f(x)>b的解集为(-1,3),求实数a、b的值. 21.(本小题满分12分)如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:km). (1)设∠AMN=θ,试用θ表示∆AMN的面积(不必化简),并写出θ的范围; (2)当工厂与村庄的距离最远时,工厂产生的噪声对居民的影响最小,求此时θ的值. (1)求数列{an},{bn}的通项公式; 参考答案 一、选择题 1.C;2.A;3.A;4.B;5.C;6.C; 7.B;8.A;9.B;10.D;11.B;12.C. 二、填空题 13.36;14.等腰直角;15.32;16.9. 三、解答题 17.(1)在直方图中,由第3组的高,可知其频率为0.25,则n=50÷0.25=200.故a=5÷200÷10=0.002 5,b=25÷200÷10=0.012 5. (2)平均数为5×0.125+15×0.19+25×0.25+35×0.23+45×0.18+55×0.025=5×(0.125+0.57+1.25+1.61+1.62+0.275)=5×5.45=27.25,估计全市家庭平均用水量为27.25立方米. 20.(1)由f(1)>-4,可得a2-6a-7<0,解得-1 22.(1)当n=1时,由S1=a1=2(a1-1),可得a1=2. 当n≥2时,an=Sn-Sn-1=2(an-an-1),得an=2an-1,故{an}是以a1=2,公比q=2的等比数列,通项公式为an=2·2n-1=2n. 由题意,有a1b1=(1-1)21+1+2=2,解得b1=1. 当n≥2时,anbn=(a1b1+a2b2+…+anbn)-(a1b1+a2b2+…+an-1bn-1)=[(n-1)·2n+1+2]-[(n-2)·2n+2]=n·2n,可得bn=n,即数列{bn}的通项公式为bn=n.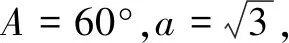
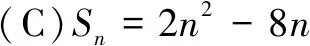

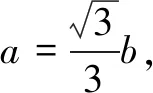
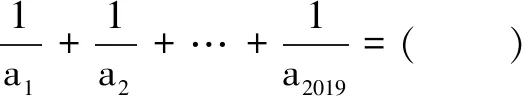
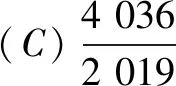
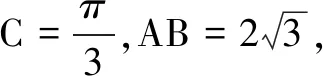
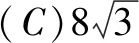
二、填空题(本大题共4小题,每小题5分,计20分)
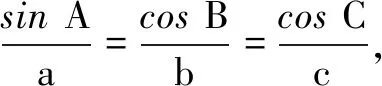
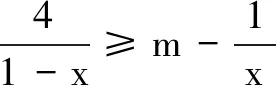
三、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)