基于ANSYS Workbench的大型香蕉筛动力学分析*

彭 飞

(唐山工业职业技术学院，河北 唐山 063299)

0 引 言

振动筛作为主流的筛选设备被广泛应用于选煤行业，主要用于煤块的分级、脱水和脱介。通常筛宽3.6m以上的振动筛认为是大型振动筛，大型振动筛能够有效提升处理能力，节省厂房面积，减少振动筛的数量和前期基建投入的费用，因此振动筛的大型化是振动筛的发展趋势之一[1-2]。

大型振动筛对整体结构性能的要求更高，尤其是加强梁、侧板等关键受力部件，往往容易发生断裂或者疲劳破坏，这就对其结构的精细化和优化提出了更高的要求。有限元分析作为较为成熟的分析方法，在振动筛的动态特性、疲劳强度等方面的分析发挥了重要作用。

本文以BVB3661振动筛为例，通过模态分析与谐相应分析，有效提高振动筛的可靠性，并为整体结构的优化和调整提供重要参考。

1 有限元模型的建立

1.1 有限元模型的建立

振动筛的零部件较多，在建模的过程中省略掉了一些对分析结果影响不大的零件，比如角钢连接板、横梁座板等。由于侧板、驱动梁、横梁等部件上的孔容易造成应力集中，在建模过程中也进行了省略。本文采用自由网格划分方法对轴进行划分，控制Body Sizing为100 mm。建立完的有限元模型共有1683864个节点，82922个单元，网格单元质量较好，能够比较精确的进行计算。各部分材料的参数设置见表1所列。

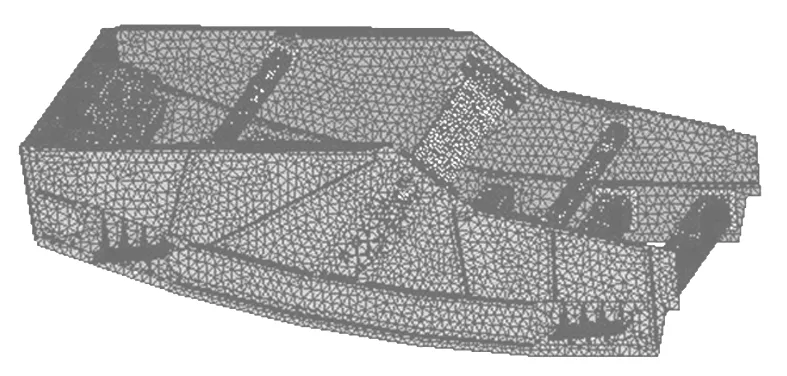
图1 振动筛有限元模型

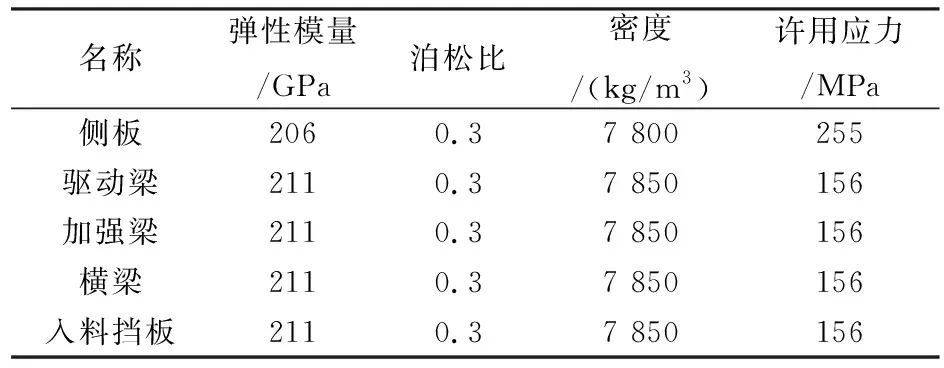
表1 材料物理特性

1.2 边界条件的设置

在振动筛前支座和后支座的位置以Body-Ground的形式添加四个弹簧，用来模拟振动筛的橡胶弹簧。在驱动梁的支撑架上方添加两个质量点，用来模拟箱式激振器的质量。并在质量点上添加远程作用点，激振力的作用点位于此位置。振动筛的激振力来源于激振器内偏心块的离心力。

P(t)=Σm0rω2sinωt

(1)

式中：P(t)为激振力；m0为偏心块的质量；r为偏心块的偏心距；ω为偏心块的角速度。

2 模态分析

振动筛是典型的振动机械，此文中对该振动筛进行了模态分析，得到其各阶振型和固有频率，以防止出现共振。进计算，得到振动筛的前12阶振型的固有频率如表2所示。

表2 固有频率计算结果

振动筛的激振力频率为13.8 Hz，由表2可知与激振力频率最相近的固有频率是15.8 Hz，与激振力频率相差14.5%，超过了设计要求10%，满足使用要求。从分析结果可以看出，前3阶固有频率接近0 Hz，主要是振动筛沿X轴、Y轴、Z轴的刚体平动，第4～6阶为振动筛绕X轴、Y轴、Z轴的刚体转动，第7～8阶为入料端和出料端的左右摆动，第9阶为筛箱整体的扭曲，第10～11阶为筛箱中后部加强梁和横梁部分的左右摆动，第12阶为中后部加强梁的扭曲。随着固有频率的增大，振动筛振动产生的最大位移也在逐渐增大。但是振动筛的工作频率较低，所以我们一般只关注振动频率附近的固有频率和振型[3-5]。图2列出了第7～10阶的振型图。

图2 模态振型图

3 谐响应分析

设置频率范围为0～30 Hz，间隙为30次，采用完全法进行谐响应分析。完全法相较于模态叠加法而言，其结果更加准确，且不局限于模态分析得到的阶数，但耗时略长。经计算，得到工作频率13.8 Hz下的等效应力如图3所示。可见整体应力分布较均匀，最大应力为17.95 MPa，位于驱动梁内部的加强筋上，如图4所示。除此之外，加强梁和侧板中后部分布应力相对较大。从振动筛Z轴位移分布云图5可以看出，振动筛在Z轴方向上位移接近于零，说明振动筛横摆很小，设计合理。从总体位移云图6看出，筛箱总体位移在4～5 mm左右，与设计振幅相符[6-8]。

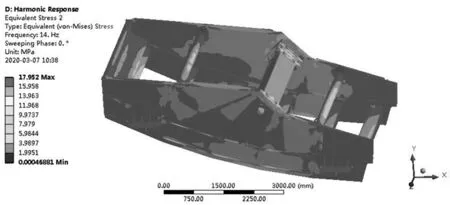
图3 13.8 Hz频率下振动筛应力分布云图

图4 驱动梁应力最大处

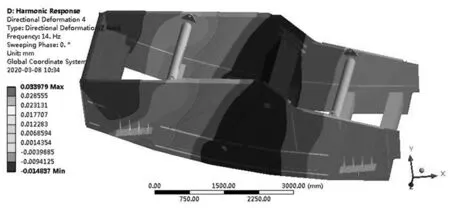
图5 Z轴方向的位移云图

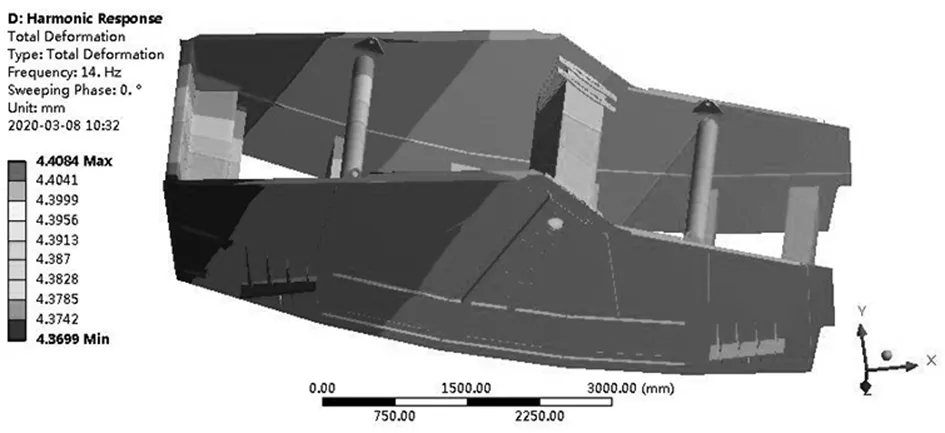
图6 总位移云图

4 组合分析

通过模态分析和谐响应分析可以得到不同频率的简谐力下的动态响应，这为我们分析振动筛的动态特性提供了参考。而要想得到任一时刻筛箱的应力分布，需要对振动筛做动力学分析，振动筛由于模型大、受力复杂，做瞬态动力学分析会对计算机提出较高要求，耗时也会较长。因此本文利用组合分析的方法模拟振动筛的应力分析。

由受力分析可知，振动筛在运行过程中主要受到激振力、惯性力、阻力、弹簧约束力及重力的作用，建立力学模型可知：

(2)

式中：{P(t)}为激振力；M为箱体和物料的质量之和；∑m0为偏心块质量之和；K为弹簧刚度；μ为阻尼系数，一般取μ=0.2～0.3。

将式(1)代入式(2)，得：

=∑m0rω2sinωt

(3)

由于振动筛是在激振力作用下做强迫振动的，仅考虑强迫振动因素，则式(3)的特解为：

Y=Asin(ωt-α)

(4)

式中：A为振动筛的振幅；α为位移滞后于激振力的相位差。

由式(4)可得：

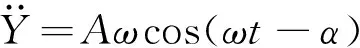
(5)

(6)

将式(4)、式(5)和式(6)代入式(3)得:

(7)

(8)

经计算，α≈0，由此可知位移滞后于激振力的相位差接近于零，而阻力相对于激振力和惯性力较小可以忽略。因此我们在分析时可以采用对筛箱在激振力、惯性力和重力作用下的组合来模拟其总体的受力情况。激振力和惯性力是简谐力，采用Harmonic Response模块，重力为恒力，采用的是Static Structural模块，然后添加Design Assessment模块，将几种情况进行组合求解。

由图7可知，重力作用下筛箱的最大应力为14.69 MPa，位于侧板与前支座结合的部分。由图8可以看出在惯性力作用下振动频率为13.8 Hz时，筛箱最大应力为1.29 MPa，位于筛箱侧板后下方的加强角钢上。筛箱的整体应力较小，这是由于惯性力不像激振力是集中作用在驱动梁上的，而是按质量分布作用于每个部分。由此也可以看出惯性力对于振动筛整体的应力分布影响较小。

图7 重力作用下的应力云图

图8 惯性力作用下的应力云图

将激振力、惯性力和重力几种工况在Design Assessment模块下进行组合求解，选择工作频率为13.8 Hz，并调整相位角，经计算得到组合工况下的应力分布如图9所示。可以看出最大应力为23.26 MPa，小于许用应力，符合设计要求。最大应力位于驱动梁支撑座上安装激振器的孔附近，此处同时受到激振力和激振器的惯性力的作用，因此出现了较大的应力。除此之外，各个横梁、加强梁处和侧板处应力分布较均匀，说明筛箱整体结构设计比较合理。

图9 组合工况下的应力分布云图

5 结 语

以BVB3661大型香蕉筛为研究对象，对其进行了模态分析，得到了前12阶振型和固有频率，验证了工作频率下不会发生共振。然后对其进行了谐响应分析，得到了13.8Hz工作频率下的振动筛的应力响应和位移响应，其数值能满足振动筛的强度和刚度要求。最后将激振力、惯性力和重力作用下的几种工况进行组合求解，进一步分析了筛箱的应力分布，验证了其强度符合设计要求，为筛箱结构的设计和优化提供重要参考。