地铁A型车轮对疲劳强度分析*
黄志丹
(兰州交通大学 机电工程学院,甘肃 兰州 730070)
0 引 言
近年来,随着地铁运营里程数的不断增加,地铁列车的安全性和可靠性也日渐受到人们关注。轮对作为地铁列车最关键的组成部件之一,不仅承载着车体、车内各种设备及乘客重量,还负责着地铁列车在轨道上的走行和导向,其“两轮一轴”利用过盈配合来传递扭矩和横向力的结构特性决定了轮轴强度对地铁列车运行的安全性和可靠性具有较大影响。
笔者以使用较广的地铁A型车轮对作为研究对象,采用结构有限元的方法[1-2]对其静强度和疲劳强度特性进行理论研究。建立地铁A型车轮对三维实体有限元模型,并对其过盈配合下轮轴强度进行校核计算,基于国际铁路联盟UIC510-5标准,采用疲劳极限法并参照车轮Goodman疲劳极限图,校核车轮疲劳强度。最后参照欧洲EN13103标准,计算车轴主要截面的疲劳应力,对比车轴材料的许用疲劳应力,考量该车轴疲劳强度是否满足设计要求[3-6]。
1 A型车轮对强度有限元分析
此文以A型车拖车转向架的轮对为分析对象,车轴材料为EA4T(屈服极限420 MPa,强度极限650 MPa[7-9]),车轮为整体辗钢轮,辐板为S形,踏面为LM型磨耗型踏面,车轮名义直径(滚动圆直径)为840 mm,允许磨耗到限直径为770 mm,车轮材料为R9T(屈服极限580 MPa,强度极限900 MPa,许用应力352 MPa[10])。A型车轮对有关技术参数如表1所列。

表1 A型车轮对技术参数
地铁A型车轮对利用过盈配合来传递扭矩和横向力,其原理是通过过盈量对接触面形成压力,从而使接触面间产生摩擦,轮对即可通过该摩擦力传递扭矩和横向力。轮轴通过过盈配合联接,接触区域已由弹性变形变为了塑性变形,接触面压应力呈现轴向方向上两端高中间低的分布规律。故基于UIC510-5标准,采用非线性的方法,对轮对过盈配合强度进行分析[11]。
建立A型车轮对的实体模型,再对轮对模型进行网格划分,模型离散单元数为372 359个,节点数为572 731个。处理后轮对离散模型如图1所示。

图1 A型车轮对实体模型及离散模型
国内标准规定铁道列车在运行过程中车轮与车轴不发生脱离或相对转动,轮轴之间需要保证足够的的接触压应力。最小接触压力计算公式如下:
(1)
式中:σ为接触面压应力;H为轮对所受横向力;R为轮毂半径;M为轮对所受扭矩;L为轮轨接触面长度;μ为轮轨接触面摩擦系数。
地铁A型车轮对相关参数为H=75.18 kN,R=92.25 mm,L=138 mm,M=12 348 kN·m,μ=0.15,由此计算出A型车轮轴最小接触压应力σmin=12.795 MPa。通常轮对的压装过盈量为0.2~0.3 mm,根据国内标准要求,轮对最小过盈配合时接触面最小压应力应大于上述应力值,且最大压低于材料许用应力,即轮对过盈配合紧固度满足要求[12-14]。分别选取轮轴过盈量0.2 mm和0.3 mm,接触模型选用增广拉格朗日乘子法对轮对过盈配合紧固度评估,σ0.2=22.049 MPa,且σ0.3=322.94 MPa,均符合国家标准要求。
国际铁路联盟UIC510-5标准中规定了车轮经过直线、曲线和道岔三种疲劳强度计算的载荷工况。如图2所示。各工况载荷垂向力和横向力值计算公式如下:
fz=1.25Q0
(2)
工况1:直线运行工况:
fY1=0
(3)
工况2:曲线运行工况:
fY2=0.7Q0
(4)
工况3:道岔运行工况:
fY3=0.42Q0
(5)
式中:Q0为轮重;Fz为轮轨垂向力;Fy为轮轨横向力。地铁A型车轴重G为16 t,由此可得轮重Q0=78.4 kN,根据公式(2)~(5)计算各工况载荷如下表2所列。载荷作用位置及方向如图2所示。

图2 各工况载荷作用位置及方向

表2 A型车轮对各工况载荷
依据UIC510-5标准对轮对加载,同时考虑过盈量对轮对静强度的影响,取最大过盈量0.3 mm。工况组合如下:
(1) 直线工况1:轮轨垂向力fZ1+最大过盈量0.3 mm。
(2) 曲线工况2:轮轨垂向力fZ2+轮轨横向力fY2+最大过盈量0.3 mm。
(3) 道岔工况3:轮轨垂向力fZ3+轮轨横向力fY3+最大过盈量0.3 mm。
按UIC510-5标准对轮对加载,同时考虑过盈量对轮对静强度的影响,选取最大过盈量0.3 mm进行计算。得出各工况下轮对应力最大值及其出现位置如表3所列,最大应力值出现工况(工况2)如图3、4所示。

图3 工况2轮对等效应力图 图4 工况2车轴等效应力图

表3 A型车各工况下轮对等效应力最大值及其出现的位置
从表3中可以看出各工况下应力最大值均出现在轮毂外侧边缘分别为323.89 MPa、338.79 MPa和335.54 MPa,均小于车轮所用材料的屈服极限(580 MPa)且有较大裕量;车轴各工况下等效应力最大值分别为147.23 MPa、283.62 MPa和147.4 MPa,均没有超过车轴所用材料的屈服极限(420 MPa)。故地铁A型车的车轮、车轴静强度均满足设计要求。
工况2下车轴最大应力出现在轴颈与防尘板座过渡区其值为283.62 MPa,车轴最大等效应力出现了一个较大的跳动,由此可见工况2(曲线工况)是地铁A型车轮对最危险的工况。建议在设计地铁A型车车轴时适当增大轴颈与防尘板座过渡区域的圆弧半径。
2 A型车车轮疲劳强度分析
承受交变载荷的工程构件,绝大多数是在随机载荷作用下服役,疲劳破坏是其主要的失效形式。
根据UIC510-5标准规定了基于无限寿命设计准则的疲劳极限法,用以评估整体车轮疲劳强度。其方法为:①分别计算上节所确定的3种工况载荷下各节点的主应力;②分别计算所确定的3种工况载荷下各节点的最大主应力;③分别计算所确定的3种工况载荷下各节点的最小主应力;④通过最大主应力和最小主应力计算各节点的平均应力和应力幅[1],公式如下:
(8)
(9)
式中:σmax为各工况载荷下疲劳考核部位节点的最大应力值;σmin为各工况载荷下疲劳考核部位节点的最小应力值;σM为各工况载荷下疲劳考核部位节点的平均应力值;σa为各工况载荷下疲劳考核部位节点的应力幅值。
按上述方式计算出各工况疲劳考核部位节点的应力参量后,判断车轮各部位的平均应力值和应力幅值是否均在Haigh-Goodman疲劳极限图(如图5所示)的包络线之内,即可评估车轮疲劳强度特性是否满足规定要求。

图5 Haigh-Goodman疲劳极限图
图中,σ0为车轮材料所对应的屈服极限(R9T材料为580 MPa);σb为车轮材料所对应的抗拉强度(R9T材料为900 MPa);σw为车轮材料所对应的疲劳极限(R9T材料车轮加工得到时为450 MPa,轧制得到时为315 MPa)。
确定直线、曲线和道岔三种疲劳载荷工况,同时考虑轮轴最大过盈配合的影响。以工况2为例,计算疲劳计算工况2下地铁A型车车轮的等效应力计算云图、最大主应力计算云图和最小主应力计算云图,如图6~8所示。

图6 疲劳计算工况2下地铁A型车车轮等效应力计算云图 图7 疲劳计算工况2下地铁A型车车轮最大主应力计算云图

图8 疲劳计算工况2下地铁A型车车轮最小主应力计算云图
根据各工况下车轮等效应力、最大主应力和最小主应力计算结果,提取车轮加载断面和顺时针绕过180°断面上主要节点(A1:辐板与轮辋过渡区外侧、A2:辐板与轮辋过渡区内侧;B1: S型辐板中间区域外侧、B2: S型辐板中间区域内侧;C1:辐板与轮毂过渡区外侧、C2:辐板与轮毂过渡区内侧;D1:轮毂孔轮轴接触面外侧、D2:轮毂孔轮轴接触面内侧)的最大与最小主应力值。并根据疲劳极限法,计算各节点的平均应力σM和应力幅σa。结果如表4(以工况2为例)所列。
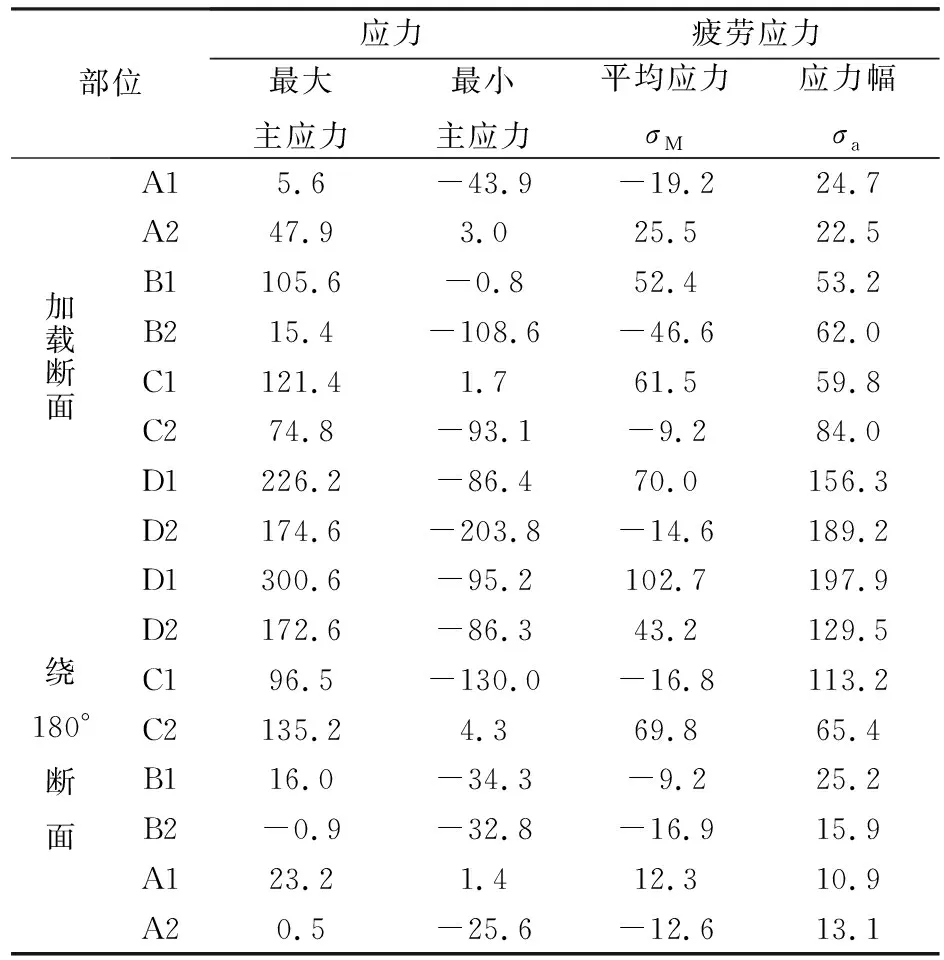
表4 工况2下地铁A型车车轮主要节点疲劳应力计算结果 /MPa
将各疲劳计算工况下地铁A型车车轮选取节点的平均应力σM和应力幅σa输入 Haigh-Goodman疲劳极限曲线图中,结果如图9所示为地铁A型车车轮Haigh-Goodman疲劳极限图。计算结果显示A型车车轮轮毂孔的疲劳应力是最大的,由此可见轮轴过盈配合对车轮的疲劳强度影响较大,在工况2时轮毂孔疲劳应力呈现最大,故可知车轮在受力较复杂的工况下时,车轮轮毂孔处的受力比其他区域要恶劣的多,因而在设计A型车车轮时应多考虑轮毂的疲劳强度。
由图9可知,地铁A型车车轮选取节点的疲劳应力状态均在该车轮材料(R9T)所对应的Haigh-Goodman疲劳极限曲线图的包络线内,故地铁A型车车轮满足无限寿命设计的要求,车轮疲劳强度足够。
3 A型车车轴疲劳强度分析
车轴通过过盈配合将两个车轮联接在一起组成轮对,共同承载着车体、车内各种设备及乘客的重量。本文根据欧洲EN13103标准规定的非动力车轴的设计规范,集合地铁A型车为踏面制动的特点得到各截面的计算方法如下(图10为车轴受力分析示意图,x轴为轨道纵向方向,y轴为轴向方向,z轴为竖直方向)。

图10 车轴受力分析示意图
对A型车非动力车轴进行分析,需要考虑以下两种类型的载荷:
(1) 运动质量载荷
(10)
(11)
(12)
(13)
由运动引起的弯矩计算公式如下:
踏面滚动圆外侧:
Mxx=P1y
(14)
踏面滚动圆内侧:
Mxx=P1y-Q1(y-b+s)+y1R
(15)
(2) 制动载荷
由制动引起的弯矩计算公式如下:
踏面滚动圆面外侧:
Mx′=ffτy
(16)
My′=0
(17)
Mz′=ffτy
(18)
踏面滚动圆面内侧:
Mx′=ffτ(b-s)
(19)
My′=0.3P′R
(20)
Mz′=ffτ(b-s)
(21)
合成弯矩计算计算公式如下:
(22)
A型车的车轴为实心轴,故车轴选取截面应力按式(29)计算:
(23)
式中:K为应力集中系数,对于圆柱面K=1,截面变化处K>1,如图11为两圆柱面过渡,图12为退刀槽过渡,参照EN标准计算公式如下:

图11 两圆柱面过渡 图12 退刀槽过渡
两圆柱面过渡:
(24)
式中:X=r/D,Y=D/d。
地铁A型车车轴材料为EA4T。轴重为16 t,轴颈直径为130 mm,防尘板座直径为150 mm,轮座平均直径为184.5 mm,轴身直径为158 mm。按上式计算车轴疲劳相关参数如表5所列。

表5 地铁A型车车轴疲劳计算相关参数
选取A型车车轴上的主要截面进行校核,包括轴颈,轴颈与防尘板座的过渡区,防尘板座,防尘板座与轮座的过渡区,轮座,轮座与轴身的过渡区和轴身,如图13所示。

图13 A型车车轴疲劳校核截面注:图1~10为车轴疲带校核截面编号,该编号配合表6说明截面位置。
计算车轴上运动引起的弯矩Mxx,制动引起的弯矩Mx′、My′、Mz′,合成弯矩MR以及各截面的应力σ。表6为A型车车轴各截面应力集中K参数,表7为A型车车轴各截面应力计算结果。表8为地铁A型车车轴(EA4T)不同位置的疲劳极限值。

表6 A型车车轴各截面应力集中参数
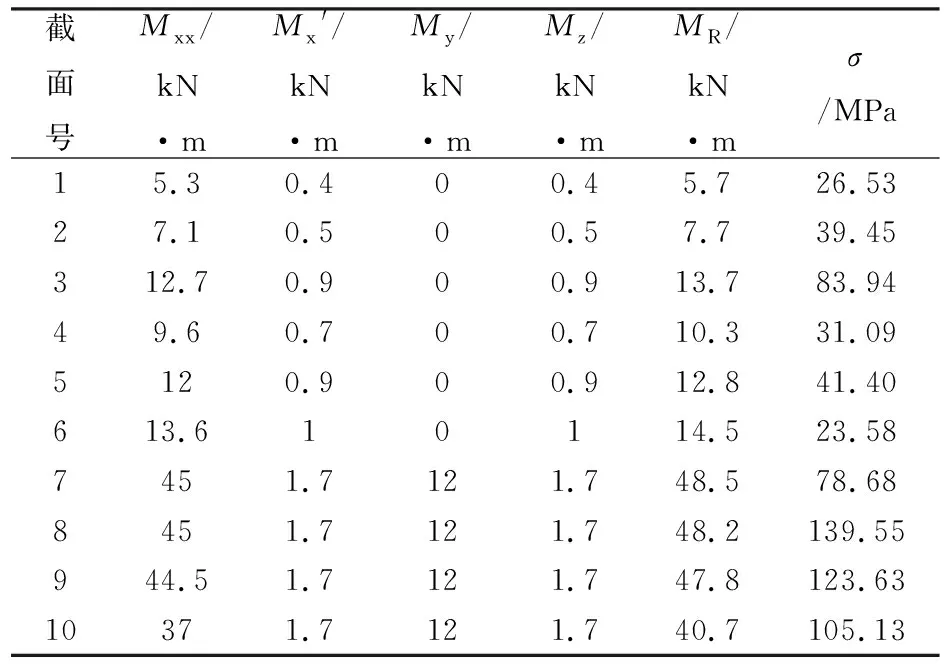
表7 A型车车轴各截面应力计算结果

表8 A型车车轴关键位置疲劳极限值(MPa)
根据表7地铁A型车车轴各截面应力计算结果,并参照表8地铁A型车车轴(EA4T)不同位置的疲劳极限值,可得以下结论:
(1) 车轴轴颈截面1、2、3处应力分别为26.53 MPa、39.45 MPa和83.94 MPa,均小于车轴对应位置疲劳极限值。
(2) 车轴防尘板座截面4、5处应力分别为31.09 MPa和41.40 MPa,均小于车轴对应位置疲劳极限值。
(3) 轮座截面6、7处应力分别为23.58 MPa和78.68 MPa,均小于车轴对应位置疲劳极限值。
(4) 轴身截面8、9、10处应力分别为139.55 MPa、123.63和105.13 MPa和,均小于车轴对应位置疲劳极限值。
(5) 截面3和截面8均为两段圆弧过渡,应力值分别为83.94 MPa和139.55 MPa,仍低于轴端压装表面疲劳极限值113 MPa和轴身疲劳极限值240 MPa。故地铁A型车车轴各截面应力计算结果满足EN13103标准规定,车轴疲劳强度符合设计要求。
4 结 论
以地铁A型车的轮对为研究对象,对其疲劳强度特性进行理论分析研究得到以下结论:
(1) 建立地铁A型车轮对的实体模型,并计算校核其过盈配合强度,结果表明,最小过盈时的接触压应力满足国内过盈配合标准,最大过盈时的接触压应力低于材料许用应力,轮轴过盈配合满足要求。基于国际铁路联盟标准UIC510-5中确定的3种计算工况对地铁A型车轮对有限元模型施加指定的约束和载荷,并考虑最大过盈配合的影响,进行轮对静力学强度分析,各工况下轮对最大等效应力均低于材料许用应力,轮对静力学强度满足设计要求。
(2) 参照国际上车轮疲劳强度分析的方法,基于UIC510-5标准确定的三种疲劳载荷工况对地铁A型车车轮进行有限元计算。采用疲劳极限法,求出在三种疲劳计算工况下车轮主要节点的平均应力σm和应力幅值σa,并将其绘画在车轮材料所对应的Goodman疲劳极限图上,这些点均位于该Goodman疲劳极限图的包络线内,因此地铁A型车车轮满足无限寿命的设计,车轮疲劳强度满足设计要求。
(3) 参照欧洲EN13103标准对地铁A型车拖车车轴进行疲劳强度评估。受力分析考虑了运动质量载荷与制动载荷的集合,选取车轴主要截面,分别求取其在两种载荷下垂直X、Y和Z轴平面的弯矩,利用合弯矩公式得到合成弯矩MR,从而计算出所选取截面的疲劳应力,其值均小于车轴材料的许用疲劳应力,车轴疲劳强度满足设计要求。

