三角桁架门式起重机结构的计算及测试分析
曹 明,胡静波
(南京市特种设备安全监督检验研究院,江苏 南京 210019)
起重机属于机电类特种设备,广泛用于交通、电力、建筑、港口等生产流通领域。门式起重机是起重机中最常见的型式之一,包括金属结构、运动机构、电气系统和安全保护装置等部分。其中金属结构一般占整机重量的70%以上,起到支撑整机和承载吊重的双重作用。
一直以来,对起重机金属结构安全性的计算、评价和研究都是业内关注的重点。传统上,对于起重机金属结构的设计计算是采用材料力学理论计算方法,但其中会有很多经验公式和简化算法可能会导致计算结果与实际情况的差别。近年来,随着计算机和仿真技术的发展,计算机有限元越来越多的应用在起重机金属结构的计算中。该方法可建立起重机的实际模型,通过设置不同的边界条件和载荷分布获得起重机的应力分布情况。但在使用这种方法时,考虑到计算机的算力问题,也会对模型进行一定程度的简化,同时边界约束条件的设定是否正确也直接影响计算结果的正确性。检验机构在对金属结构进行评估时,一般会采用现场应力测试,以电测法为主,通过在金属结构上贴应变片后现场加载的方式,可获得贴片位置结构的实际应力值,但该方法存在现场贴片难度大以及测点选择的随机性等问题。本文将这3种方式同时应用于金属结构的计算与分析中,并对其结果进行验证和比对。
门式起重机主梁类型分为箱型、桁架和型钢等3种型式。桁架结构具有良好的稳定性和较小的迎风面积,通常用于露天施工现场。本文选取MQ50-32A3型桁架式门式起重机为分析对象,其额定起重量为50t,跨度为32m,工作级别为A3,材质为Q235B。
1 材料力学计算
该起重机的主要参数如下:
起重量:PQ=50t;
大车跨度:L=32m;
小车自重:PXC=5000kg;
主梁自重:PZL=12580.5×2=25161kg;
桁架全高度:H=2315mm。
1.1 主梁截面特性
主梁截面如图1所示,根据此图纸尺寸计算主梁截面特性。
截面总惯性矩为:Ix=Ix1+Ix2+Ix3=2379696.87cm4;Iy=Iy1+Iy2+Iy3=257944.94cm4。
1.2 强度计算
计算小车在跨中吊起额定载荷的工况,对此时上弦杆、下弦杆和腹杆上各自的跨中部位即最大受力处进行分析。
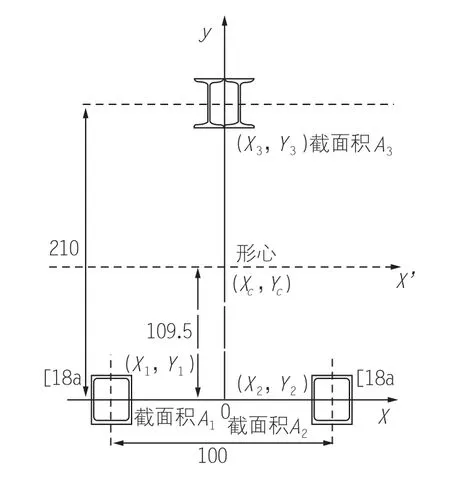
图1 桁架截面
(1)上弦杆。

(2)下弦杆。
最大受拉处结构强度
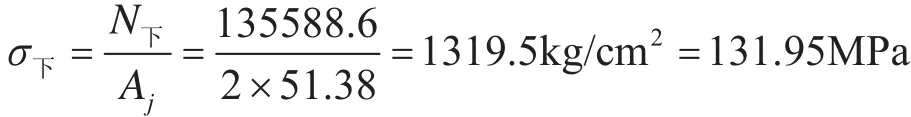
(3)斜腹杆。

2 有限元计算
2.1 模型建立
该起重机的主梁和支腿间采用高强度螺栓连接,为方便模拟计算,建模时可简化为刚性连接。主梁托架与支腿、支腿与拉杆、支腿与稳定杆之间的连接通过圆柱销连接,在建模时将圆柱销连接简化为刚性连接。按照起重机实际尺寸在有限元分析软件ANSYS中建立几何模型。
根据结构类型的不同,在软件中采用不同的网格划分方式:采用Sweep方式对起重机的上弦杆、腹杆以及小车轨道进行网格划分;采用hex-dominant方式对下弦杆、主梁托架、主支腿进行网格划分;对其他零部件选择自由方式划分。对于不同位置的零部件调节网格尺寸大小,最终划分后的网格模型包含2244880个节点、755760个单元,如图2所示。
2.2 边界条件及加载
按照Q235的常规属性进行材料设置:密度为7.85×103kg/m3,弹性模量为2.06×105MPa,泊松比为0.3。该起重机的主梁两端与支腿通过高强度螺栓连接,在有限元分析的建模阶段已经被简化为刚性连接,不需要再额外进行约束。在静刚度测试过程中,大车机构处于静止状态,在分析时可在大车车轮处施加不同的约束。在试验过程中,理论上大车车轮与轨道应当始终保持接触,因此固定约束所有车轮的重力方向自由度和沿轨道方向的自由度,约束一边支腿2个车轮垂直于轨道方向的自由度,另一边支腿不应约束该自由度。
因为在起重机静力试验时没有考虑到风载和振动等特殊载荷,因此在模拟仿真时也只需要考虑包括起重机自重载荷和额定载荷在内的常规载荷即可。主梁及附件自身质量作为自重载荷处理,小车质量和起吊的额定载荷一起作为集中载荷加载在小车的4个车轮处。
2.3 强度计算结果
考虑小车在跨中起吊额定载荷工况,计算后的整机Von Mises应力分布如图3所示,从该图可以主梁上弦杆以及下弦杆应力分布比较均匀,在跨中及附近位置应力比较大。主梁跨中上弦杆局部应力分布如图4所示,从图中可见除轮压处最大应力为146MPa外,其他应力都分布在100MPa左右;跨中下弦杆局部应力分布如图5所示。从图中可见,最大受拉处的应力为106MPa。
3 应力测试
采用电测法进行起重机现场应力测试。该结构为桁架结构,主应力方向明确,贴片方式采用沿主应力方向贴单片应变片。参考理论计算和有限元分析结果确定17个测点,测点分布如图6所示。
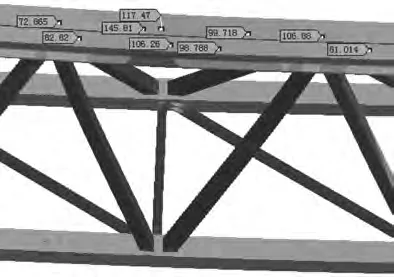
图4 主梁跨中上弦杆局部应力云图
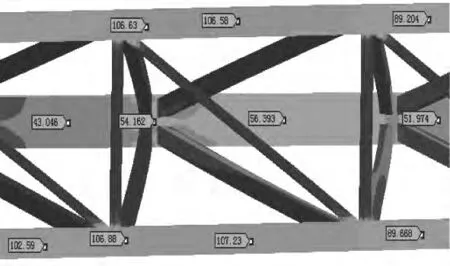
图5 主梁跨中下弦杆应力云图

图6 桁架应力测试测点分布图
应力测试选用静态应变测试仪作为测试仪器,采样频率为1s。电测法应力测试获得的应力为工作应力,因此需要尽量避免小车自重的影响。在测试过程中,首先将起重小车停在主梁端部,调整测试仪器,记录应变片空载状态下的读数;接着将起重小车开至跨中部位,起吊额定载荷,待数据稳定后,记录额载跨中时应变片读数。选取跨中部分测点的测试结果见表1。其中结构应力值为测试应力值加上结构自重应力的结果,结构自重应力可从有限元分析获得。负数代表测点受到压应力,正数代表测点受到拉应力。
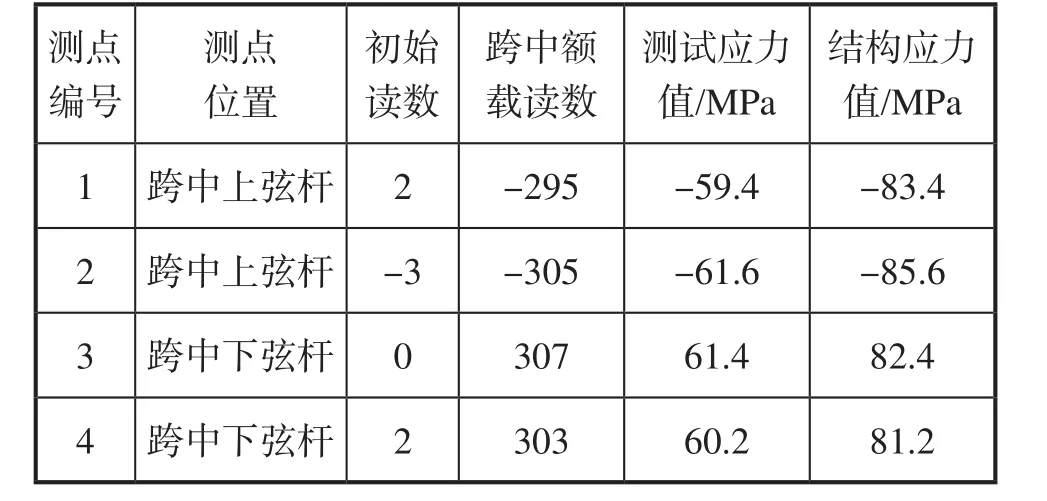
表1 部分测点静态应力测试结果
4 比较分析
根据起重机械设计规范,金属结构的安全系数为1.48。该起重机的金属结构材质为Q235B,其屈服极限为235MPa,则结构的最大许用应力应为158.8MPa。假定应力测试选点的测点1—测点4分别为理论计算和有限元计算中上下弦杆的最大应力点,则结构的允许值、材料力学计算、有限元分析和现场应力测试结果比较如图7所示。
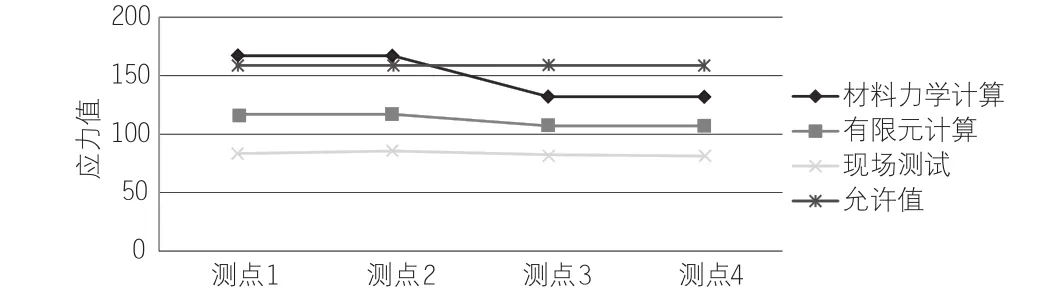
图7 3种方法各位置应力比较
从图7可以看出,材料力学计算方法的保守程度最大,现场应力测试结果相对偏小。以下弦杆受拉位置即测点3为例,材料力学计算结果为132MPa,有限元计算结果为107MPa,而现场应力测试结果为82.4MPa,应力测试与材料力学计算差值达37.5%。
材料力学的计算结果偏大是由于使用了较多的保守经验公式和简化方法,使得计算结果可能与现实情况有一定的偏差。计算结果偏于安全,这在设计中是完全可以接受的,但同时也有可能会造成一定的材料浪费。有限元计算结果与材料力学方法的结果偏差可能来源于模型的简化程度和网格划分的合理性,现场应力测试数据偏小可能是由于现场贴片的位置和角度与理论有所偏差。相对来说,有限元计算结果更接近结构现场的现实情况。
5 结束语
本文以材料力学方法、有限元分析和现场应力测试的方法对同一桁架门式起重机的金属结构进行了分析。通过3种方法结果的比较可知,有限元模拟分析方法对起重机金属结构进行计算更快捷和方便,但同时也应当采用理论计算和现场测试的方法对有限元分析方法的结果进行验证。本文的分析过程和结论可为同类型起重机金属结构的设计、检测和安全评估提供新的思路和途径。

