基于组合分类策略的个人信用风险评估研究

钟金宏, 邵晶晶, 李兴国

(合肥工业大学 管理学院， 安徽 合肥 230009)

0 引 言

目前，居民在消费类贷款、住房贷款、汽车贷款上的需求量不断增大。据国家统计局数据[1]显示,截至2017年年末,个人短期贷款达68 041亿元,比上年同期增加18 724亿元,个人中长期贷款达247 154亿元,比上年同期增加45 993亿元,个人贷款总额占全年境内各项贷款的31.58%。由此可见,个人贷款规模增长迅速,未来个人贷款业务有望成为中外金融机构竞争的焦点。由于个人贷款业务发展前景巨大,导致各种骗贷、套现、倒贷等欺诈手段层出不穷。根据中国银行业监督管理委员会(简称“银监会”)数据统计[2],2008—2017年银行业不良贷款余额如图1所示,说明近年来金融行业不良贷款余额总体呈上升趋势,且涨幅较大。因此,定位出不良客户、评估贷款人的信用成为当前亟待解决的问题。

图1 2008—2017年银行业不良贷款余额

信用评估是关于信用好坏的二元分类问题,目前已有很多分类算法应用到信用评估问题中,但不同的分类算法有着不同的适用场景,在不同数据集上不能全部展现理想的分类效果,无法适用一般情况。考虑到实际生活中个人信用数据会受不同国家和地区的影响这一特殊性,本文选取了信用评估中具有代表性的K最近邻(K-nearest neighbor, KNN)、随机森林(random forest, RF)、决策树(decision tree, DT)和支持向量机(support vector machine, SVM)等算法作为基分类器,通过组合分类模型评估贷款人信用,提高对实际信用数据更适用的基分类器在最终组合决策中的作用。该模型充分利用各个算法的优势,适合解决现实生活中的贷款人信用评估问题。

1 信用评估方法

在信用评估问题上,早期的评估模型分为如下2类:

(1) 基于专家评分。这类模型的特点是由专家列出评判贷款人信用的特征,再针对每项特征由专家对贷款人打分,根据得分确定贷款人信用好坏。文献[3]根据贷款人的能力、资金状况和个人条件,结合专家意见,分别从学历、职业、职称、工作稳定性;住房、交通工具、有价证券、银行存款、年收入;年龄、性别、婚姻状况、赡养人数、投保状况等评价指标量化贷款人的信用级别。

(2) 基于期权定价模型,常用的有Black-Scholes-Merton (BSM)模型、信用监测模型(credit monitor model, KMV)等。这类模型主要应用于个人抵押贷款或对公贷款的信用评估问题中,通过计算出个人抵押品价值或公司的股价、负债等市场价值总和来得到贷款人或公司的理论违约距离和理论违约率,以达到信用评估的目的。文献[4]通过实证分析表明KMV模型基本能够识别上市公司的信用状况,但识别能力有限,建议结合公司财务数据综合度量更加可靠。文献[5]在BSM模型基础上提出一种“B-S期权定价+预留协作+保证金”契约机制,进一步验证了期权定价模型可以得到理论违约率,保证电网公司收益的同时,降低市场价格波动带来的风险。

随着互联网金融的兴起和大数据时代的到来,早期评估模型基于其有主观依赖和时效滞后等缺点,难以适应现阶段贷款需求量大、产品种类多、贷款规则复杂等情况,而各种数据挖掘技术、机器学习算法被应用到信贷审批领域,能够克服传统统计模型的局限性,不但能处理海量数据,而且使信用风险得到识别和量化,在复杂的情况下展现了良好的效果[6]。

目前应用在信用评估问题上的常用分类器有KNN、逻辑回归(logistic regression, LR)、线性判别分析(linear discriminant analysis, LDA)、SVM、RF、DT、神经网络等。文献[7]展现了KNN在信用评估下的效果略优于逻辑回归,并认为KNN有较大的商业用途；文献[8]对比分类算法发现,RF适合处理非平衡信用数据集,对违约项目的识别能力较好；文献[9]证明运用决策树的ID3算法,建立信贷客户信用评估系统,能进行科学、高效的信用评估分类；文献[10]验证了SVM在不均衡、小样本、高维模式识别问题中具有较好的预测能力。

以上基于单分类器的信用评估方法虽简单易实现,但由于单分类器对数据较为敏感,这一类方法的不稳定性较大,相比之下,多分类器的预测准确率和泛化性能均优于任一基分类器。文献[11]组合神经网络和遗传规划方法,提出两阶段的信用评估模型,表明了组合分类比单个分类器分类结果精度更高, 可解释性更好；文献[12]组合多个SVM应用在信用评估中,该算法解决了非线性支持向量机的局限性,计算成本低、分类效果好,更适用于数据集大的情况；文献[13]基于LR、DT、人工神经网络和SVM 这4个基分类器,通过比较Bagging、Boosting、Stacking 这3种集成方法在信用评估上的效果后发现,组合可以极大地提高基分类器的效果。

综上可见,尽管目前已有很多组合分类算法应用到信用评估问题上,解决了早期评估模型的局限性和滞后性，但是不同的信用评估方法有各自的优缺点[14],主要存在以下问题:

(1) 不同的分类算法有着不同的适用场景,在某个数据集上效果较好的分类器,在另一类数据集上却不一定有较好的效果,因此对于不同的数据集,需要区别对待各基分类器。

(2) 现实中贷款人的信用数据受不同国家和地区的经济、文化、发展水平以及居民消费观念等诸多因素的影响,使得很多模型中用到的贷款人特征不能适应其他数据。

本文引入组合分类策略来获得最终分类模型,每个基分类器的最终决策度根据其在数据集上的效果来确定,最终模型选取的贷款人特征根据相关度高低来确定,使得各基分类器之间形成优势互补,适应各类真实信用数据。

2 基于组合分类的信用评估模型

组合分类问题中,基分类器的选择直接影响最终的分类结果。单一分类器适合的数据区域不同,优缺点不一。本文中基分类器分别选取KNN、DT、RF、SVM等。各基分类器的优缺点对比见表1所列,从表1可以看出,这4个基分类器分别适合不同的数据区域,组合可以达到扬长避短、优势互补的目的。

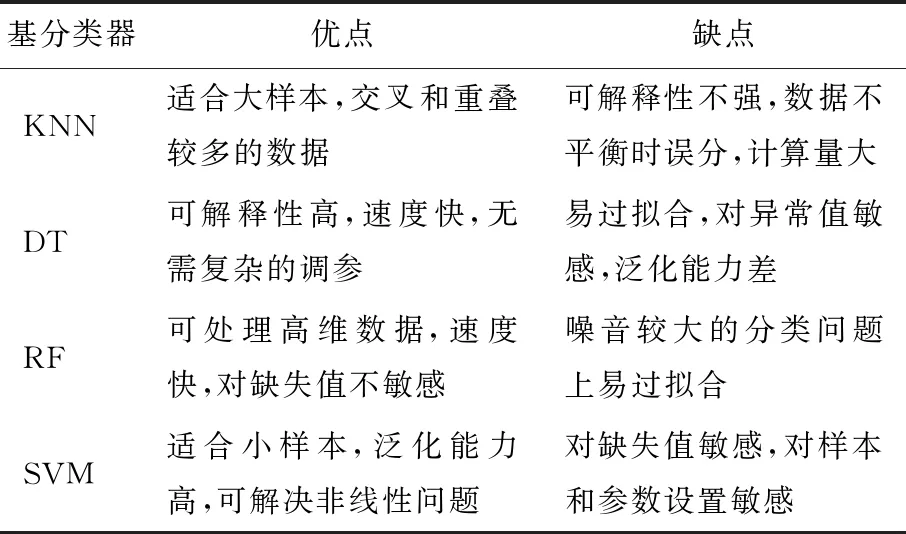
表1 各基分类器的优缺点比较

本文提出一种基于决策分值的多分类器组合(multiple classifier combination,MCC)模型，具体流程如图2所示。

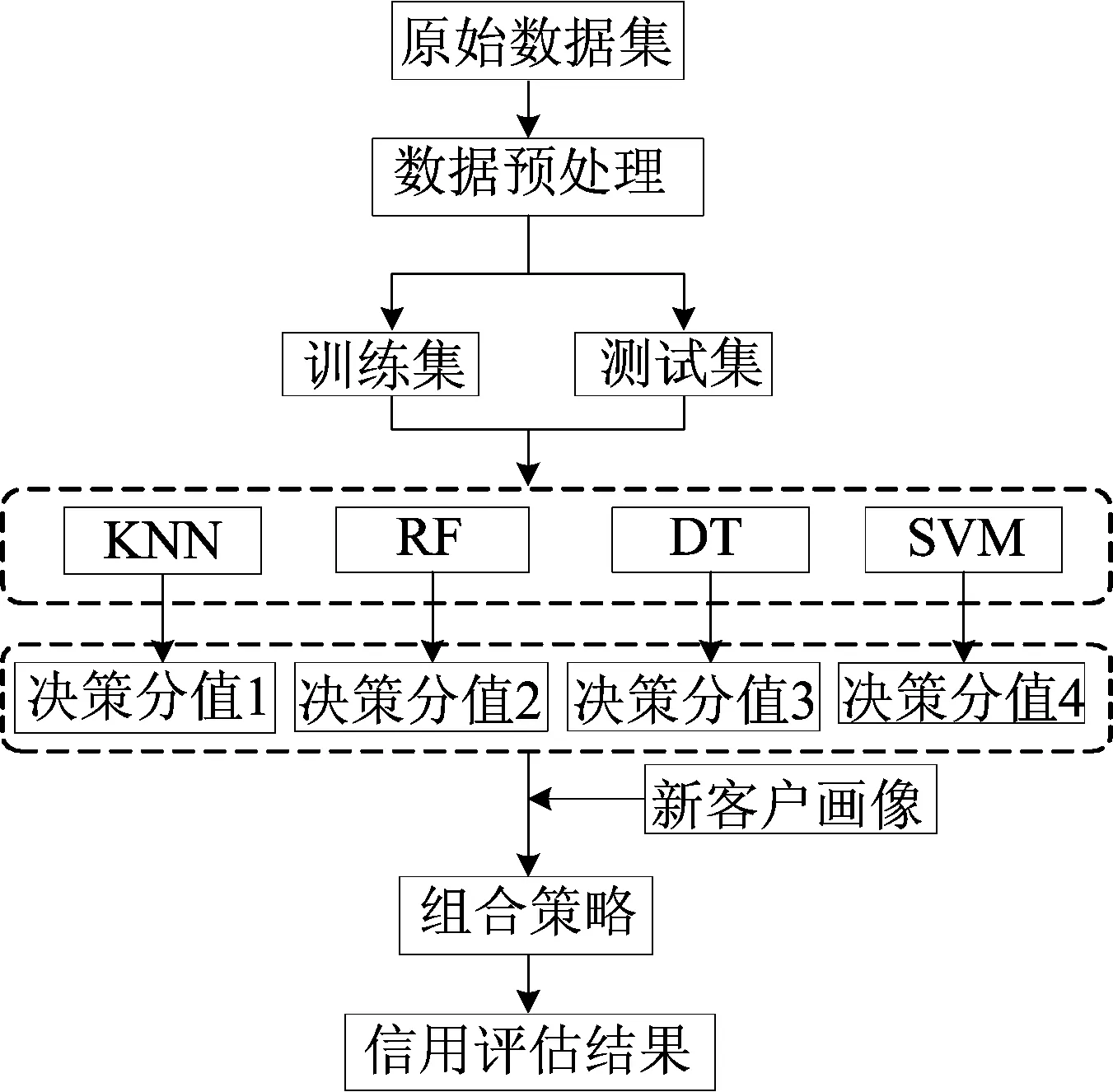
图2 MCC模型流程

该模型从2个维度量化单个分类器的可信度,并通过组合的方式进行分类器的融合,既可以提高整体分类的准确率,又能保证实际应用中的稳定性,满足金融机构判别贷款类新客户信用的要求。

2.1 决策分值

因为数据集不同,各算法对数据集的适用度也不相同,所以不同算法在同一数据集下的训练结果也有高低之分。对于多分类器而言,最终分类器决策需要提高可信度高的基分类器所占的比重,而降低相比之下可信度低的基分类器所占的比重。模型中引入决策分值的方法来量化提高或降低的比重,该方法从稳定性和准确性2个维度评判基分类器的可信度,因此模型中基分类器的最终决策分值ST(total score,)由该分类器的稳定性分值SS(stability score,)和准确性分值SA(accuracy score,)组成。

稳定性的考量是根据该分类器在同一数据集下相同规模的n份不同子数据集的训练结果计算得出,准确性的考量是根据该分类器n次训练结果的准确率高低确定的。MCC模型的决策分值计算流程如图3所示。

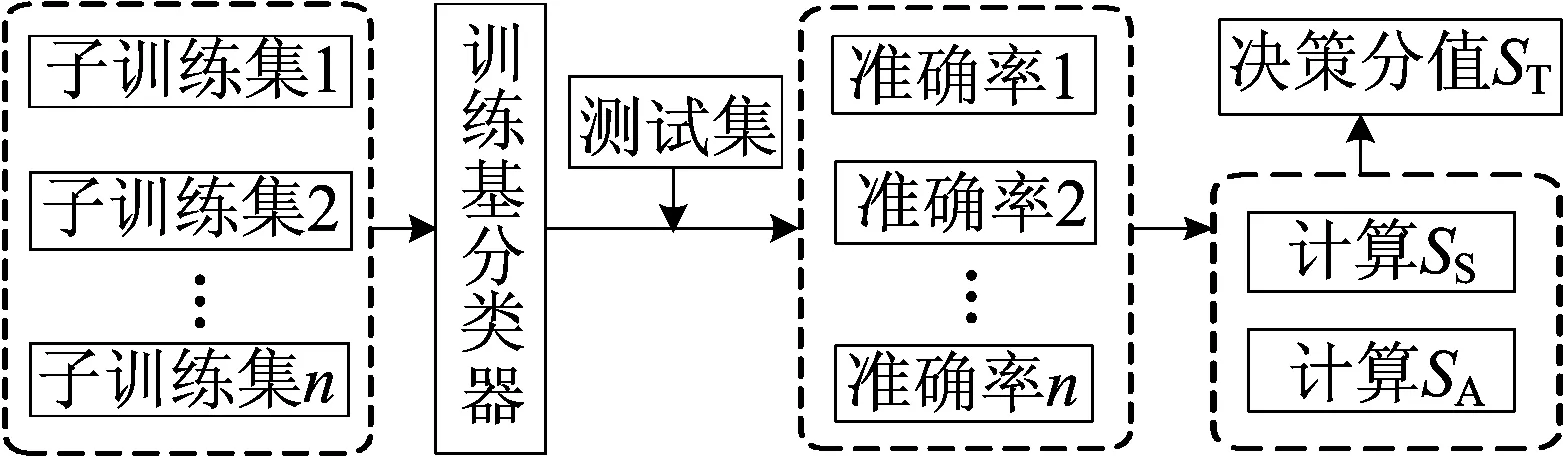
图3 计算基分类器对应决策分值流程

具体方法如下。

(1) 通过随机采样得到1份不放回的测试集和n份相等规模的平衡子训练集,测试集与训练集数量之比为1∶3。

(2) 逐个选取基分类器通过n次训练结果得出每次的训练准确率,根据公式计算出最终决策的分值,ST(ST∈(0，2))计算公式为:

STi=SSi+SAi

(1)

(2)

(3)

(4)

其中,t为分类器的个数(本文t=4)；n为子数据集个数(本文n=5);aij为第i个分类器在第j个子数据集下的准确率,j=1,2,…,n。

2.2 组合策略

在得到每个单分类器的决策分值ST后,可以直观地看出分类效果较好的分类器在最终决策中占比较大,但这只是相对而言,并且每个分类器也不可能达到100%的预测准确率。组合模型可以去除单个分类器偶然不准确的缺陷,且能充分考虑到有新用户在信用好坏临界处的现象。组合策略直接影响到最终模型的有效性,MCC模型的组合策略流程如图4所示。

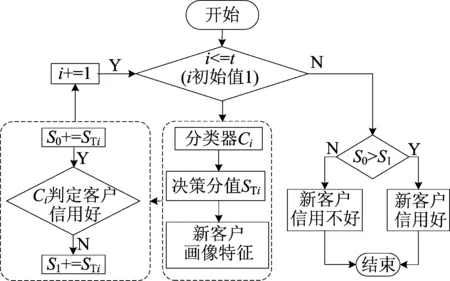
图4 组合策略流程

具体方法如下。

(1) 得到第j个单分类器的最终分值STi后,当有新客户的画像特征输入到分类器时,每个基分类器都需要判定客户信用好坏。

(2) 计算判定客户信用好的分类器决策总分值S0和判定客户信用不好的分类器决策总分值Si,计算公式为：

(5)

(6)

(3) 新客户信用f(x)通过比较S0和S1的大小来确定,公式为:

(7)

其中,m为t个分类器中将客户分为1的分类器个数；S1为所有分类器中将该客户分为1(即信用不好)的分类器总分值；S0为所有分类器中将该客户分为0(即信用良好)的分类器总分值。

本文将单分类器的优势互补,通过多组实验降低单次实验的偶然性,并从稳定性和准确性2个维度来确定各分类器在模型最终决策中的比重。

3 实验设计与数据处理

3.1 分类评估标准

分类评估标准是检验一个分类器是否能够有效分类的重要指标,本文使用准确率A、精度P、召回率R、F值4种评估标准,这4种评估标准都是基于混淆矩阵计算的,混淆矩阵见表2所列。该矩阵显示了分类算法在将输入数据分配给不同类时的性能[15]。

表2 混淆矩阵

准确率A反映一个分类器模型的总体性能,表示模型正确地分类了多少条数据,计算公式为:

(8)

精度P反映模型输出的可靠性，计算公式为：

(9)

召回率R展示了模型在实际欺诈交易检测中的有效性，计算公式为:

(10)

F值为召回率和精度的调和平均数，是一个综合评价的指标。因此F值是评价不平衡类数据的一个更可靠的指标，计算公式为：

(11)

3.2 数据集

本文选择信用评估中最具有代表性的3个数据集，分别是UCI机器学习数据库中的德国、澳大利亚、中国信用数据。原始数据集描述见表3所列。

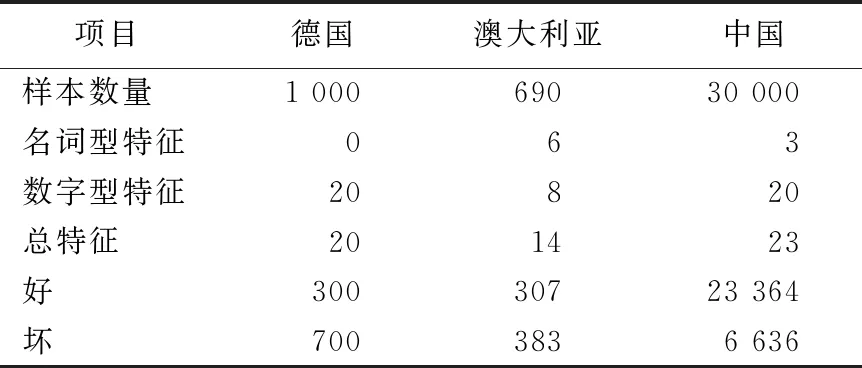
表3 信用数据集

由表3可知，3个数据集通过4个方面来描述借贷人的信息。由于澳大利亚信用数据涉及信用卡应用程序,所有属性名称和值都已更改为无意义的符号,以保护数据的机密性。本文给出了其他2个数据集的主要特征描述,具体见表4所列。

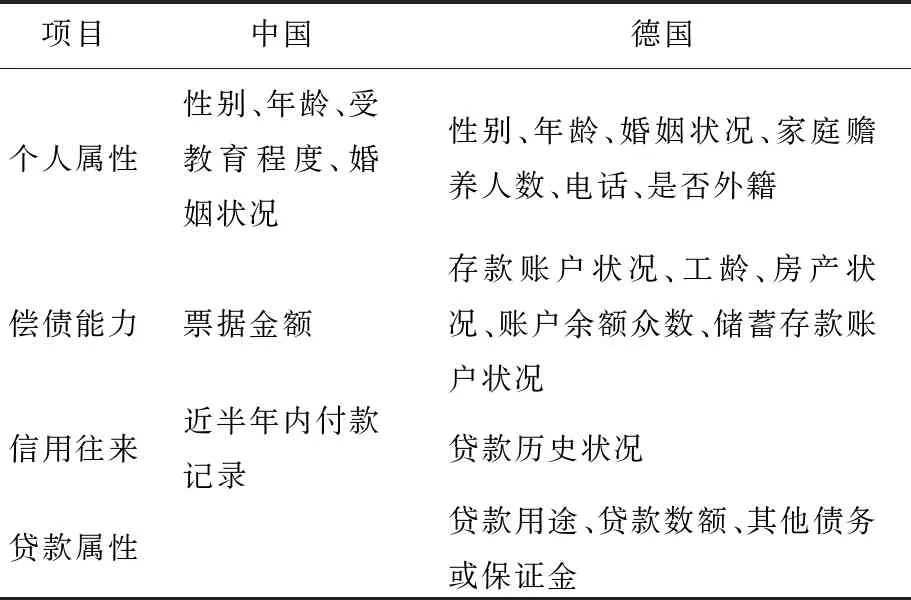
表4 数据集特征描述

3.3 数据预处理

本文首先从数据集的特征入手,3个数据集的客户画像特征分别有20、14、23个,这些属性如果全部选取,那么预测率并没有展现很好的效果,并且特征过多,也会降低模型的泛化能力,文献[16]提出了信用评估问题的关键是在考虑以往信用评分的客观事实和主观经验的情况下,客户的哪些特征对信用决策有意义。因此需要对这些特征进行加工,用最少的数据特征使准确率尽可能高。

在数据集特征选择上,本文首先根据数据集各个特征之间的相关性,尤其是各个特征与最终信用好坏的相关性。3个信用数据集特征相关关系如图5所示,具体可根据颜色深浅来直观反映各个特征之间相关性,颜色越浅代表特征之间正相关性越大,颜色越深代表特征之间负相关性越大。

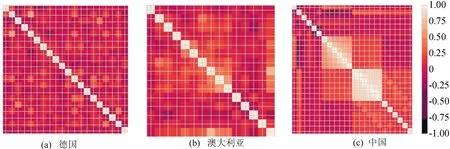
图5 各信用数据集特征相关关系

各个特征与最终信用分类相关值见表5所列。表5中的相关级别由1～7表示相关度逐级减弱。结合图5和表5可以看出,处于第1～2级别的特征相关度最高,处于第3～4级别的特征相关度较高,处于第5～7级别的特征相关度较差。根据统计发现,相关度高的特征集中在表4的偿债能力和信用往来属性中,而贷款人的基本情况、贷款属性与最终信用好坏无太大关联。本文中选择剔除相关度较差的特征,将余下特征进行下一步处理。

表5 各个特征与最终信用分类相关值

为科学评估个人信用风险,需进一步对剩下数据进行异常值检测。考虑到银行人员统计时出错或者客户避及隐私故意错填的情况,异常值的存在对于真实性数据集来说难以避免。但对于异常值敏感的算法(如决策树)来说,会产生有效性降低等负面影响。箱线图是检测异常值的一个标准,可以直观地看出正常数据是集中还是分散,通过观察各方盒和线段长短可以显示数据分布的偏态。3个数据集中存在的异常值箱型图如图6所示,由于数据集中异常值数量较少,本文选择剔除异常值数据,并将剩下的数据划分为训练集和测试集。

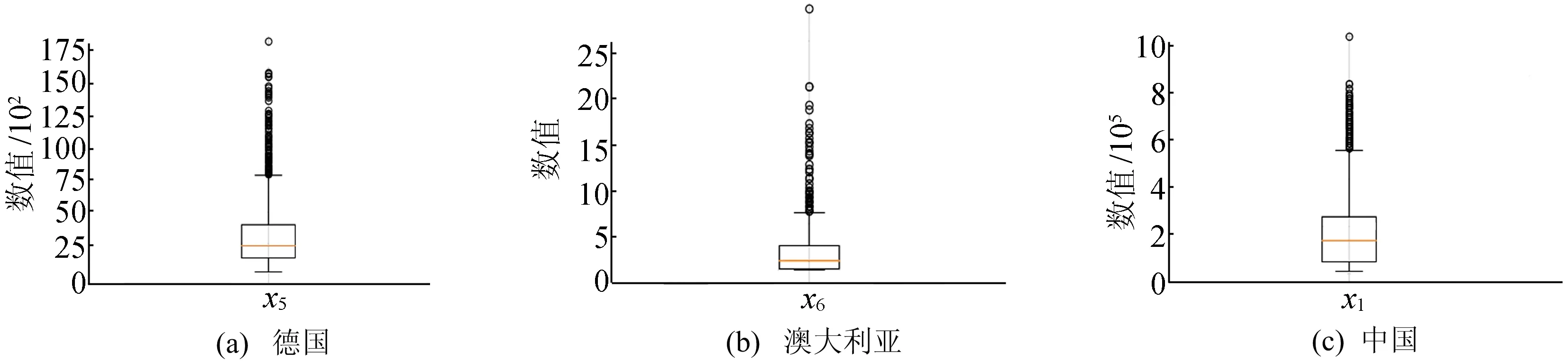
图6 各信用数据集中部分特征的箱型图

从表3可以看出,3个评估数据集均为不平衡数据集,这是由于现实生活中信用好的客户和信用不好的客户人数很难达到相等,并且大多情况下,信用好的客户人数多于信用不好的客户人数。组合分类方法与不平衡数据集具有很好的兼容性,处理不平衡数据集有多种方法,本文采用无放回的随机欠采样方法从原数据集中抽取了6份平衡子数据集,其中1份作为测试集,5份作为训练集,测试集和训练集的数据比例控制在1∶3。

4 实验结果分析

3个信用数据集下各分类器准确率及决策分值见表6所列,将决策分值对应各个分类器,在测试集下进行测试,最终分类器根据每个单分类器的判断对该客户进行信用好坏打分。

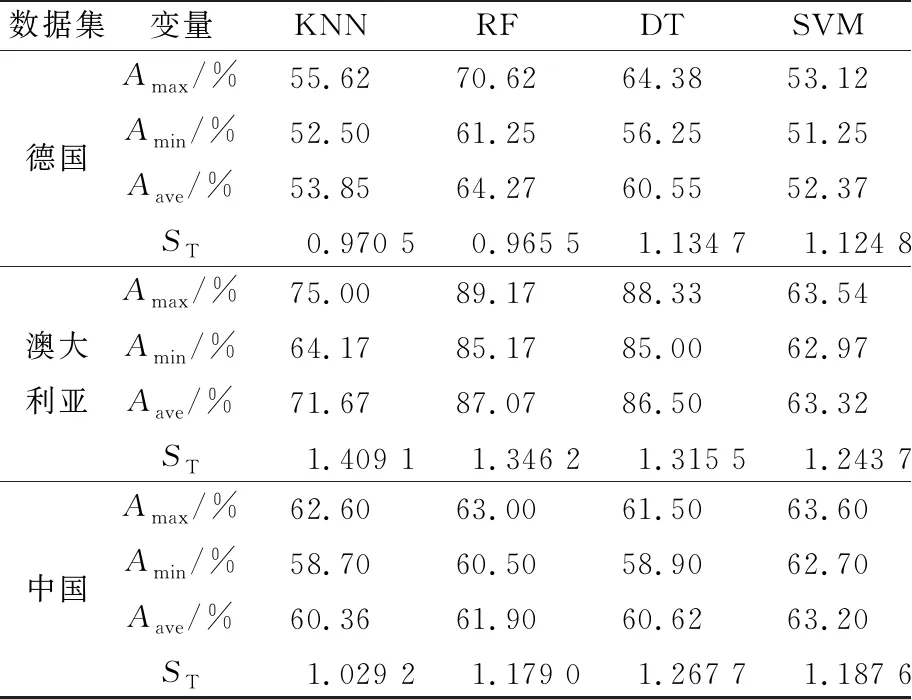
表6 各分类器准确率及总分值

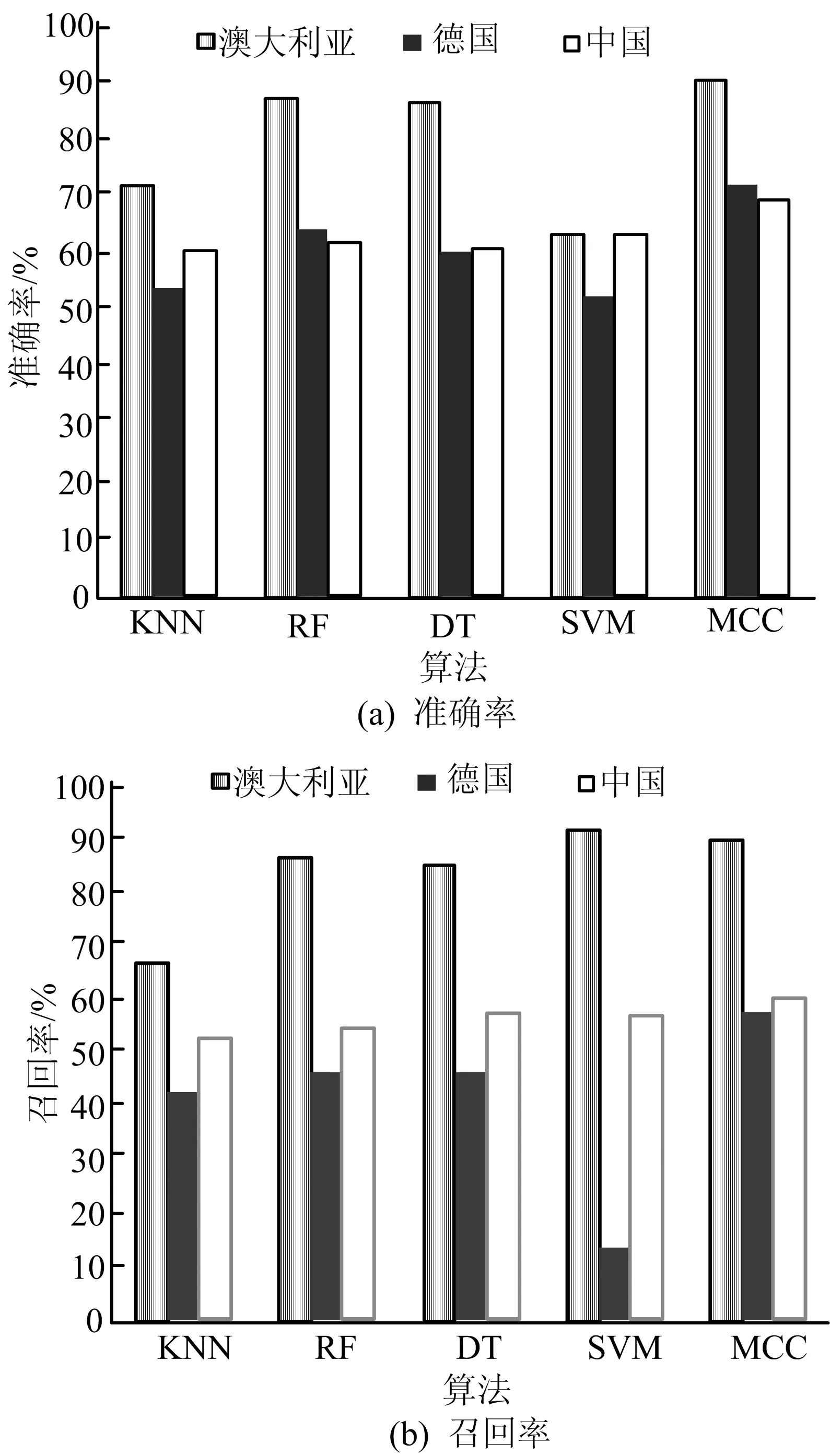
最终MCC模型与KNN、RF、DT、SVM等4个分类器的评估指标对比如图7所示,从图7可以看出,经过MCC模型的分类后,澳大利亚、德国、中国数据集的预测准确率分别达到90.40%、71.87%、69.3%,相比其他4个单分类器有了很大的提升。

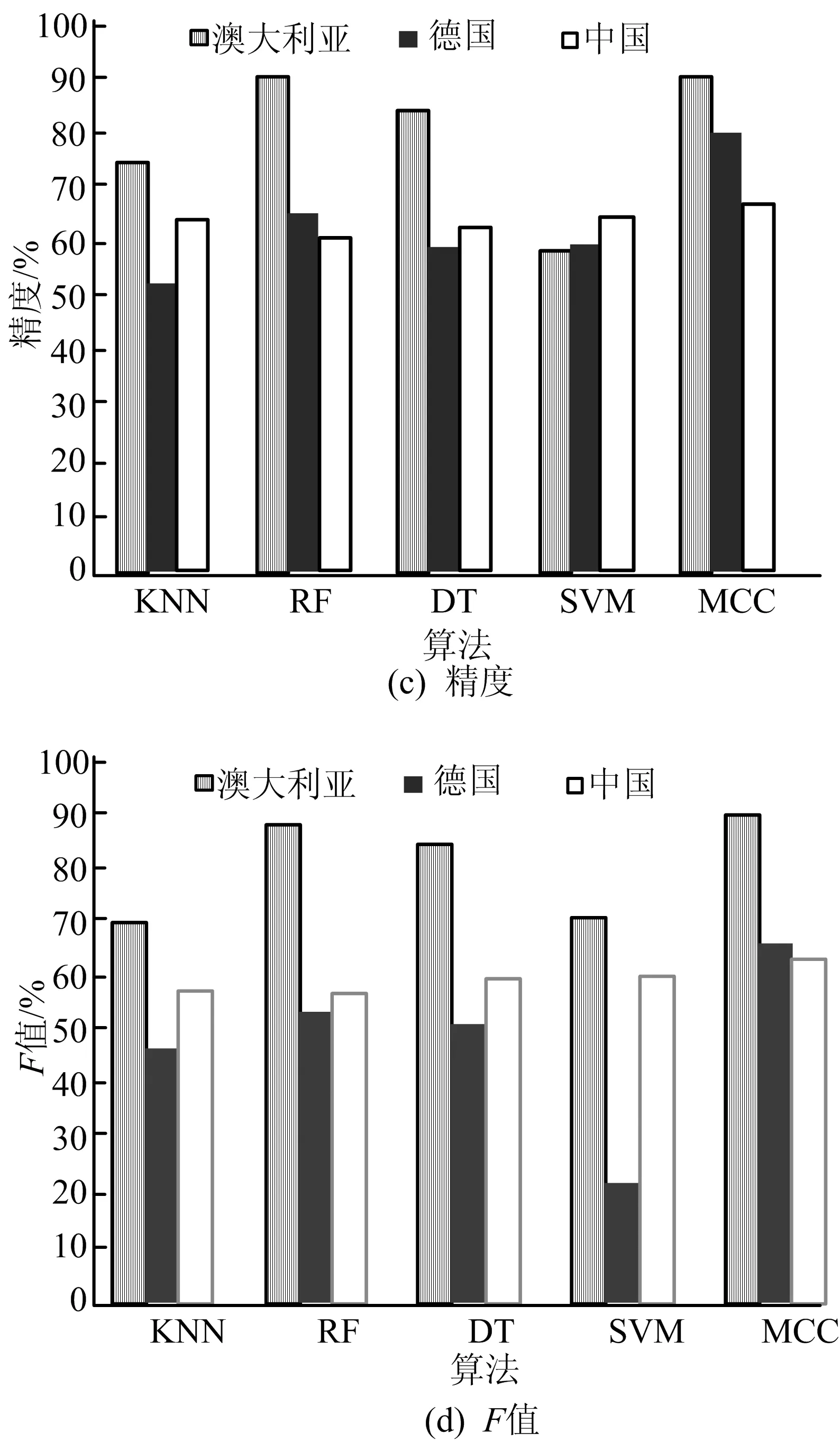
图7 各算法在数据集上的4个指标

再结合精度、召回率和F值这3个指标来看,MCC模型也表现了优良的效果,MCC模型应用在德国数据集上,相比单分类器下,准确率最少提高了7.74%,精度最少提高了14.63%,召回率最少提高了11.25%。

另外,结合KNN、RF、DT、SVM这4个单分类器的决策分值和准确率来看,决策树在信用评估问题上表现出良好的性能,其次是RF和SVM。同时也验证了前人的观点。

对于金融机构来说,即使是提高1%的预测准确率,也可以极大地降低风险和损失[17]。本文提出的MCC模型,将信用评估问题中4种常用的分类器进行组合,并且选择数据集中与最终信用好坏相关度高的特征,有效地减少了最终分类器的运行时间,提高了分类器的准确率。MCC模型将为银行等金融机构做出参考,应用到实际中去,减少人工作业成本,提高信用预测准确率,降低风险损失。

5 结 论

本文基于组合分类策略,并在组合模型中引入了决策分值的方法,将单分类器从稳定性和准确性2个维度上进行评判,避免了单分类器的不稳定性和单次实验的不可靠性。将MCC模型应用到UCI中3个真实数据集上,实验结果表明,组合后的模型准确率相比单分类器都有了明显的提升,证明了本文提出的MCC模型可以应用到实际中去,对金融机构有一定的参考作用。