基于射流冲击横流原理产生涡旋及其测量

李琪琪，梁彬烽，郭泳盈，曾 皓，苏掌旭，彭 力

(华南师范大学 a.物理与电信工程学院;b.信息光电子科技学院，广东 广州 510006)

射流是指从排泄口射出或靠机械推动射入另一流体域内的运动流体. 工业、农业和生活中的废弃流体，通常以射流的形式排放到环境流体中，例如：烟囱排入大气的废气，河流和海洋水域的污水排放，等等. 实验研究方面，Kamotani和Grebe[1]对流速比R(R为射流流速与横流流速之比)较大范围内的紊动射流宏观特性进行测量，主要结论是射流流速场和温度场不同导致射流轴线不同，并给出了射流基于速度和温度的轴线方程；Subramanya和Porey[2]，Pratte和Baines[3]系统地研究了射流轴线方程，侧重于射流的时均量研究；Andreopoules和Rodi[4-5]研究了射流的时均结构，重点测量高阶紊动量. 在流场显示方面，黄真理等[6]利用平面激光诱导荧光，对明槽水流中底孔排放的单孔和多孔射流浓度场进行了研究，观测到低速比时射流出现分叉现象和尾涡，并给出了马蹄涡结构沿水深的变化过程. 在数值研究方面,Sykes等[7]运用方程湍流模式，探讨在高流速比下横流中射流的涡动力学特性；Demuren[8]运用二阶动量矩湍流模式结合多重网格技术计算低流速比下射流的流场和温度场；彭文启[9]采用k-ε湍流模式，结合多重网格的混合有限分析法对流速比R=2的流场进行了研究，检验多重网格下混合有限分析法适用复杂流场. 目前国内外对射流冲击横流产生涡旋的实验方法，涡旋三维特征的测量研究还很少，并且多数实验为单点测量，较难捕捉到流场中大尺度涡旋结构的瞬时特征. 本文基于射流冲击横流原理，在水槽里产生了稳定的涡旋，并采用双摄像头和3D-PIV技术对涡旋的三维流场特征和结构进行研究分析，计算得到涡旋的速度环量、涡量场、线速度场以及黏度.

1 实验原理

1.1 射流冲击横流产生涡旋原理

Gaster和Crighton[10]应用了稳定性理论对射流进行分析，在流动显示中得出射流通过涡卷吸入环境水体. Pettersen(1978)[11]研究发现射流冲击横流会产生沿射流轴线运动的螺旋涡，并与涡环叠加. 所以当射流冲击横流时，在向壁面发展过程中射流边界存在涡旋的剪切层，在此区域射流与环境流体产生卷吸和混合. 射流到达壁面形成对底壁的冲击，在冲击区内流线弯曲并折转过渡到平行于壁面的壁射流流动形态，在这个过程射流与横流、固体壁面之间产生复杂的卷吸作用，从而在流动中产生了射流剪切层、横流绕流等复杂流动特征[12]. 环境横流遇到射流的阻碍形成绕流，射流由于前后边界存在压力差发生偏转，对环境水体为半无限水深情况，在水域的上下会存在压力差，导致产生涡旋.

下面利用RNGk-湍流模型[9,13]对射流冲击横流的结构进行分析. 图1为半无限横流紊动射流示意图.

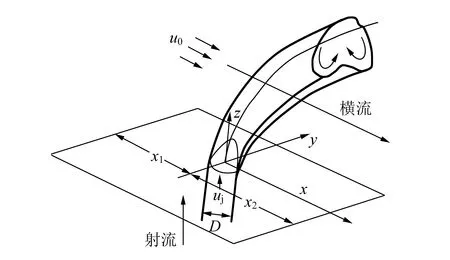
图1 半无限横流紊动射流示意图

1)在出口边界x=x2满足

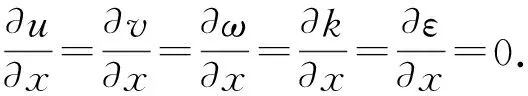
2)在底部边界z=0满足

a.当x2+y2≤D2/4时，u=v=0,ω=uj,φ=c0;

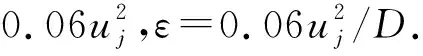
3)在上边界z=z2满足

4)在对称面y=0，v=0满足

5)在侧平面y=y2满足v=0,ω=0,u=u0,且

由RNGk-ε湍流模型的公式分析可知，在不同边界面上(例如出口边界、底部边界、上边界等)涡旋满足的条件不相同，说明不同的边界面会产生不同的涡旋结构. 而模型中的边界面是相对射流与横流的冲击起点而言的，如果将起点看做是射流的射水口，由此可知离射水口不同的位置会有不同的涡旋结构，即射水口的位置可以影响涡旋参量. 除此之外公式中涉及到了横流速度u0，射流速度uj，因此可知横流、射流速度可以影响涡旋参量.

1.2 3D-PIV技术原理

采用粒子图像测速(PIV)技术[14]获得速度场信息，进而根据速度场分析涡旋的速度环量、涡量场和黏度，可以避免测试装置对装置内原始流场的影响，还可以对空间瞬态流场进行实时测量，深入研究装置内液体流动特性. 为了实现三维粒子图像测速(3D-PIV)[15]，对左右相机各自连续2帧粒子图像进行运动分析. 首先对左右相机同一时刻的粒子图像作粒子匹配和融合后找到对应区域，然后根据同一相机前后不同时刻对应的粒子图像作相关性分析获得粒子在平面上的位移矢量信息，最后对矢量结果进行三维重构后得到运动粒子的空间位移.

在实验中，用CMOS相机替代PIV技术中常用的CCD相机，用细小泡沫替代PIV测速技术中的玻璃微珠作为示踪粒子. 用稳定光源照亮流场，并照像记录粒子图像. 由已知的时间间隔分析得到粒子位移，即可得到示踪粒子在某点的速度矢量. 如果示踪粒子在某个已知的时间间隔出内，由位置(x1,y1,z1)运动至(x2,y2,z2)，则由示踪粒子所在处的某流体质点三维速度分量u,v,w为

当Δt→0时，即

PIV记录粒子的Lagrange速度，当粒子对流体的跟随性非常好时，可认为此速度代表流体的Euler速度. 即PIV通过测得示踪粒子的速度矢量来定量显示整个流场的流动特征.

2 理论模拟

2.1 Autodesk CFD模拟方法

CFD计算流体力学(Computational fluid dynamics,CFD)从计算方法出发，利用计算机得到流体控制方程的近似解.

模拟过程为：

a.用solid works软件建立三维模型，该模型材料为PVC，厚度为8 mm，尺寸为800 mm×300 mm×400 mm，与实际的装置相同.

b.将三维模型导入Autodesk CFD，设置好模型实验装置的初始温度、压强、边界条件(即横流与射流的速度)以及运动的方向等，得出水流模拟的轨迹运动图像. 最后分析图像，找出流速比、水箱深度与射水口位置最佳参量.

CFD建立理想化的实验模型是通过改变初始条件和边界条件等参量即可得出不同情况下的模拟效果，这可降低探究实验成本，提高实际实验的可行性.

2.2 模拟实验参量设计

随着流速比的增大，涡旋近区范围内射流向下游的偏转程度有所减小，射流入水后射流主体两侧剪切涡间的相互作用对环境流体的卷吸作用明显，更加容易形成涡旋[16]. 在模拟的过程中，结合实际情况可达到的最大射流速度为8.00 m/s. 首先在模拟装置中装入20 cm高的水，再从口径为矩形的射水口设置射流，在模拟过程中，保持射流方向与横流方向一致，从左边射向右边. 模拟实验参量设置如表1所示.

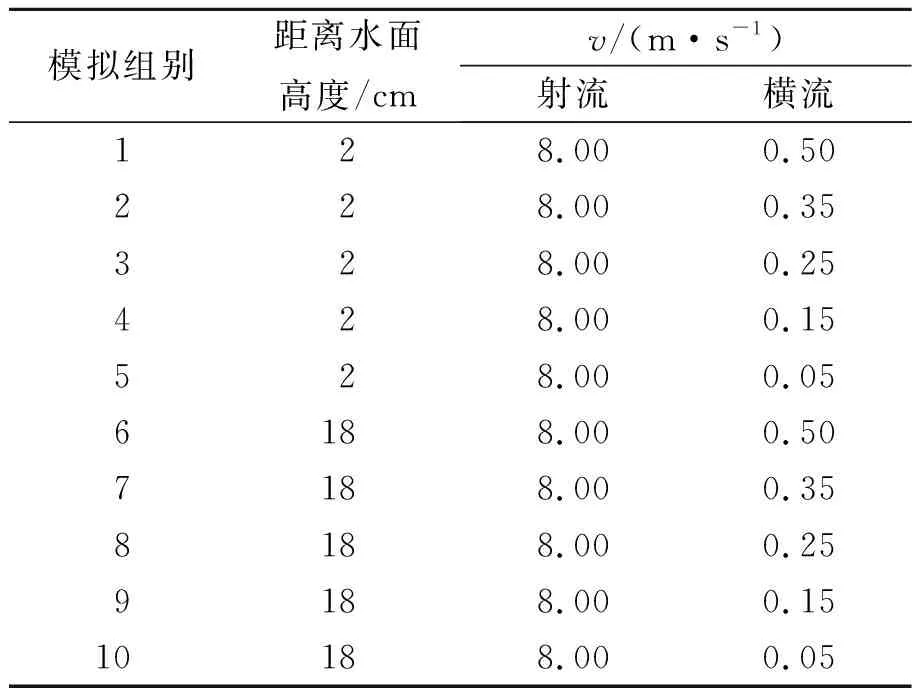
表1 参量设置

部分结果模拟如图2～3所示.三维坐标图中，不同颜色代表不同的速度，红色框内为形成的涡旋.

由图2的红色框内涡旋的形态、速度大小和明显程度可以看出：当射水口接近水面、射流速度为8.00 m/s时，横流速度越小，涡旋产生越明显，当横流速度为0.05 m/s时可以产生巨大而且稳定涡旋.

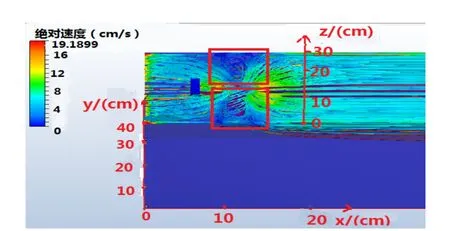
(a)横流0.50 m/s

由图3的红色框内涡旋的形态、速度大小和明显程度可以看出：当射水口靠近水底、射流速度为8.00 m/s时，横流速度越小，涡旋产生越明显，当横流速度为0.05 m/s时产生的涡旋更加明显.

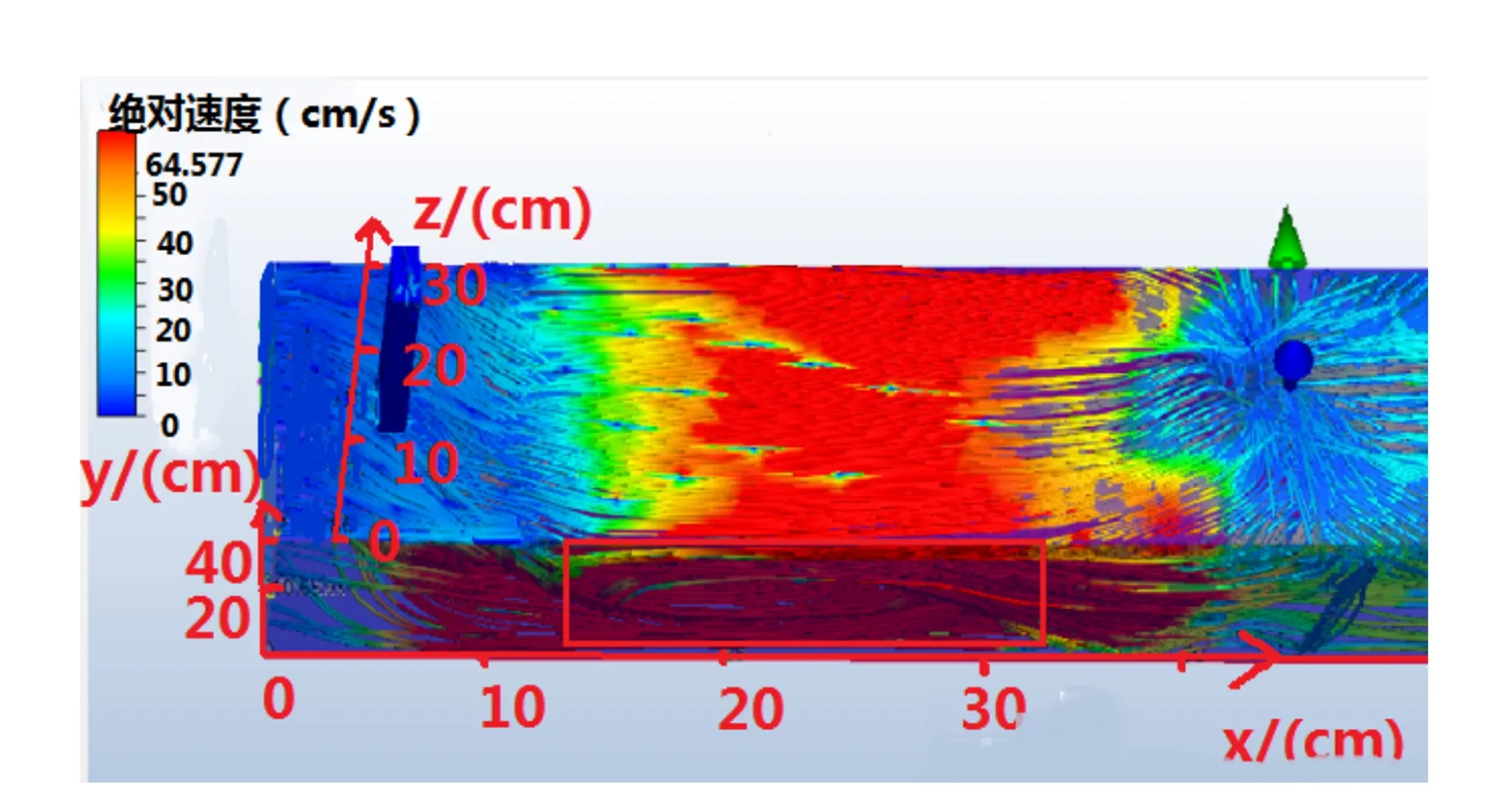
(a)横流0.50 m/s

2.3 模拟结果分析

当射流速度固定在8.00 m/s时，横流速度越小，即流速比更大，更易产生巨大稳定的涡旋，因此得到符合实验的流速为：横流流速0.05 m/s，射流流速8.00 m/s. 同时比较射水口位置接近水面和靠近水底的三维图像，可知射水口接近水面产生的涡旋在射水口两侧呈正立状态，射水口靠近水底时，产生的涡旋在水底下呈卧铺状态，考虑到涡旋的可视化和测量，最终实验选择射水口接近水面.

3 实验装置设计

3.1 涡旋产生装置

涡旋产生装置如图4所示，整体由水箱、隔板、水泵、水管、射水口和2个摄像头组成. 水箱和隔板使用PVC材料，厚度为8 mm. 水箱尺寸为800 mm×300 mm×400 mm. 隔板尺寸为400 mm×300 mm. 隔板均分水箱，使整个水箱呈回型结构，在尽量小的空间模拟环境横流. 水管连接射水口和水泵，水泵置于水箱角落，射水口置于对角的另角落，避免水泵吸水造成干扰，射水口距离水箱底部5～10 cm.

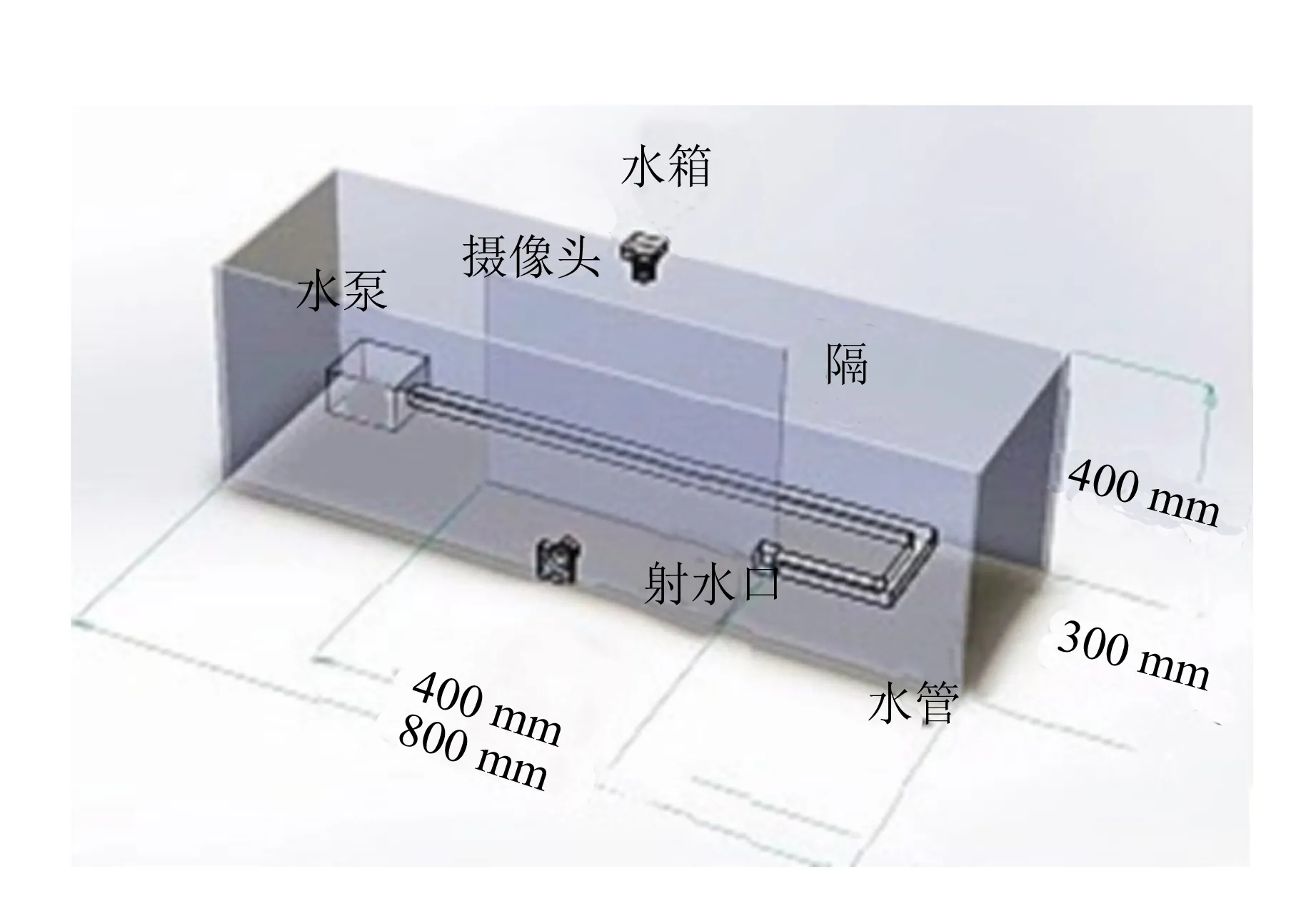
图4 涡旋产生装置整体效果图

3.2 涡旋测量装置

3.2.1 测量装置设计

使用红色泡沫为标记物，实验装置周围除了侧壁和顶部，其余部分均用黑色卡纸围住，来避免外部光源干扰. 摄像头使用普通USB摄像头，摄像头分辨率为1 280 pixel×720 pixel，帧数为20 s-1. 2个摄像头在同一平面上并保持拍摄角度垂直，分别拍摄装置侧视图和俯视图. 拍摄俯视图的摄像头距水面高度10 cm，距离侧壁15 cm. 拍摄侧视图的摄像头水平位置为侧壁与隔板的中心，即距离隔板7.5 cm. 2个摄像头通过2个USB接口与同一电脑连接.

3.2.2 测量算法设计

使用opencv颜色识别算法提取泡沫颜色(红色)区域，并且转为灰度图. 使用Sobel算子，在x方向求梯度并且进行threshold二值化处理，接着dilate膨胀1次、再erode腐蚀1次，最后再dilate膨胀1次，获得特征明显的细小泡沫区域图像.

通过findContours标记白色区域在图像中的像素点位置，并根据比例换算成实际空间坐标点. 根据2个摄像头分别获得的2组二维坐标点合成三维坐标点，并由三维坐标点判定涡旋中心坐标. 可由连续2帧图像所获得的三维坐标点计算速度向量场v. 计算某点到涡旋中心距离，并近似认为半径a. 根据速度场和以a为半径的圆计算速度环量Γ. 根据a、速度场v计算涡量场Ω. 再根据涡量场Ω计算时间t的偏导以及拉普拉斯算子▽2计算涡旋的扩散系数γ.

测量算法流程图如图5所示.

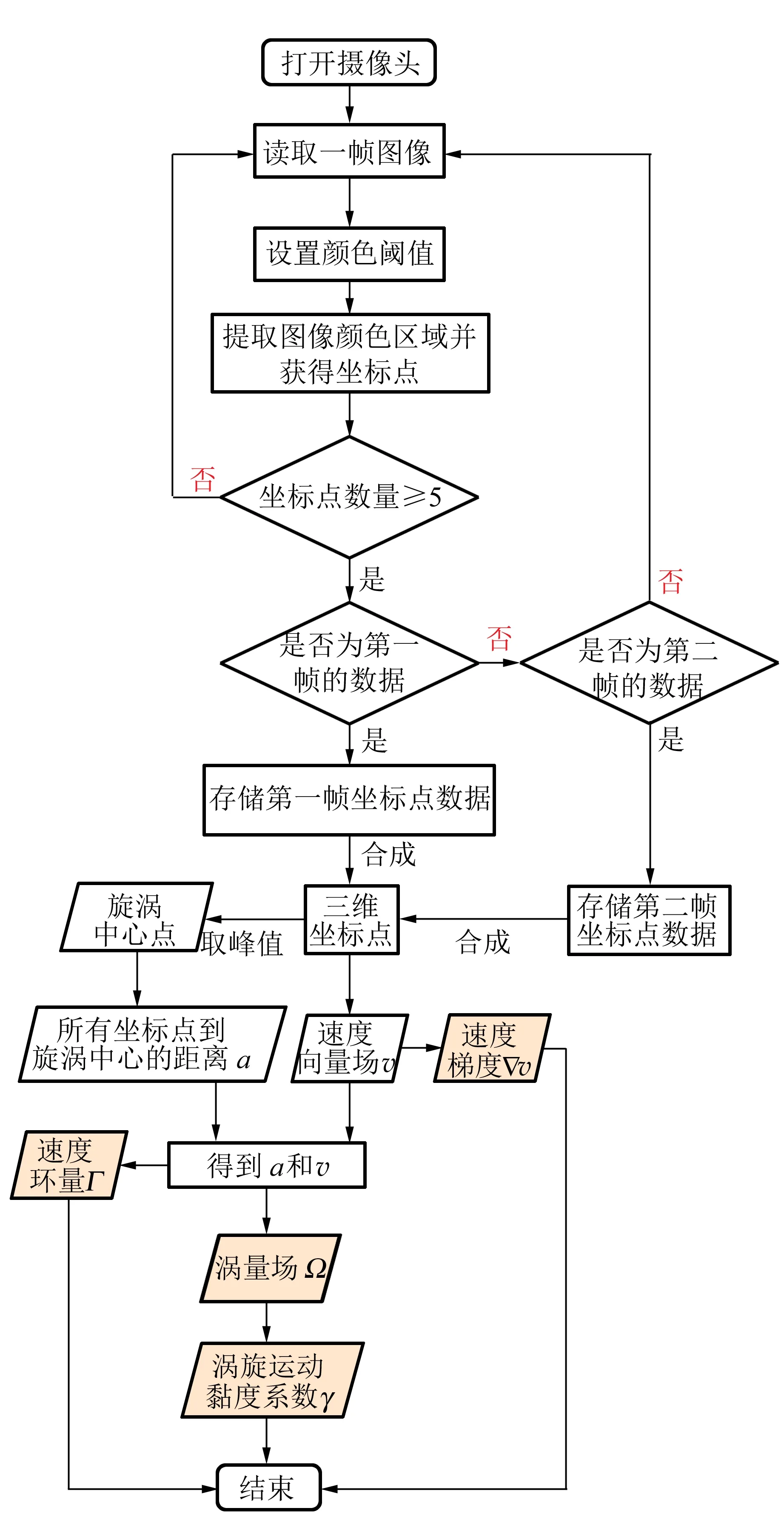
图5 测量算法流程图

4 实验操作流程

实验装置如图6所示.

图6 实际装置图

实验操作流程分为2部分：1)放入细小红色泡沫，用流速较大的射流冲击横流来产生可视化的巨大稳定涡旋；2)对巨大稳定涡旋进行相关测量.

4.1 射流冲击横流产生涡旋实验步骤

向水箱中注入20 cm高的水，加入用于可视化的红色泡沫.

打开水泵，射水口开始喷水，射水口喷射的水流速约为8.00 m/s. 水泵抽水和射水口所射出的水流会带动装置中的静水，最终使水箱中的水流速稳定在0.10 m/s，射水口喷水之后，再微调节射水口的深度和方向，直至等待一段时间后生成明显且稳定的大型涡旋，效果图如图7所示.

(a)

4.2 涡旋结构测量操作流程

打开2个USB摄像头，并连接到笔记本电脑上，根据摄像头拍摄情况来调整摄像头的焦距和位置，使2个摄像头的拍摄的图像清晰、互相垂直且宽度相等.

在生成涡旋且红色泡沫分布在涡旋附近时，点击运行涡旋测量程序，系统将自动处理该时刻的图像并获取速度环量场、线速度场、涡量场和黏度分布的数据和三维可视化图像，电脑的测量效果图如图8～9所示.

图8 带有红色泡沫的涡旋原图

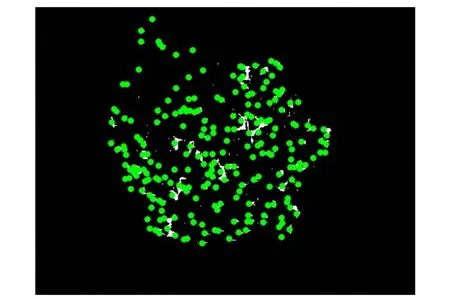
图9 坐标点标记图

5 实验数据结果与分析

经过设计的算法，系统自动对涡旋的坐标点进行处理，得到涡旋的参量.

图10是速度环量场. 速度环量是标量，有正负号，规定沿曲线顺时针绕行的方向为正方向，沿曲线逆时针绕行的方向为负方向. 图10中可看出涡旋各个标记点的速度环量，其中箭头表示方向，大部分的标记点沿着顺时针方向转动，方向向右，有小部分的标记点逆时针旋转，方向向左. 线段的长度表示速度环量的大小，由图10可知当标记点的半径越大时速度越大. 因为实验过程中用红色泡沫为标记点，标记点的运动是随机的，不一定总是沿着涡旋结构运动，所以导致标记点的运动方向并不统一，出现图10中有部分标记点运动方向相反的情况，说明测量结果的方向符合实际实验. 由于流体的黏性、斜压性以及无势外力将使速度环量随着涡旋的深入有数值上的减小，即速度环量随着曲线半径的增大而增大，因此图10的速度大小符合理论和实验结果，测量准确.

图10 速度环量场

图11是线速度场. 其方向沿运动轨道的切线方向，线段长度表示速度大小，可以表示涡旋标记点运动的快慢和方向. 由图11可以看出箭头方向沿着切线方向，涡旋外侧速度大于内部速度，这与图10中测量的速度结果相一致.

图11 线速度场

图12是涡量场. 图中线段长度表示涡量的大小，等于涡旋各点绕涡旋中心旋转的平均角速度的2倍，箭头方向表示环量方向，与涡旋的瞬时转动轴线重合[17]. 由图12可以看出涡旋各点的涡量方向都是竖直向上的，在实验中如果红色泡沫绕着涡旋做圆周运动，那么标记点的角速度方向用右手螺旋定则可知与转动轴的方向相同，即竖直向上. 由图12中还可以观察到涡旋中心轴的涡量最大，远离中心轴涡量变小，在实验观察中可知涡旋中心轴上的角速度最大，远离中心轴时角速度变小，因此参量结果符合实际实验.

图13是涡旋的黏度的测量结果. 实验中采用的液体是水，查表可知水的黏度在常温(取24.9 ℃)的标准值为[18]1 mm2·s-1，如图13红色线所画的数值. 实验中每个标记点的黏度的值由图13可知大部分集中在红色线附近，计算误差允许范围内的标记点的平均黏度为0.898 2 mm2·s-1，与水的标准值大致相同，实验测量结果接近标准值.

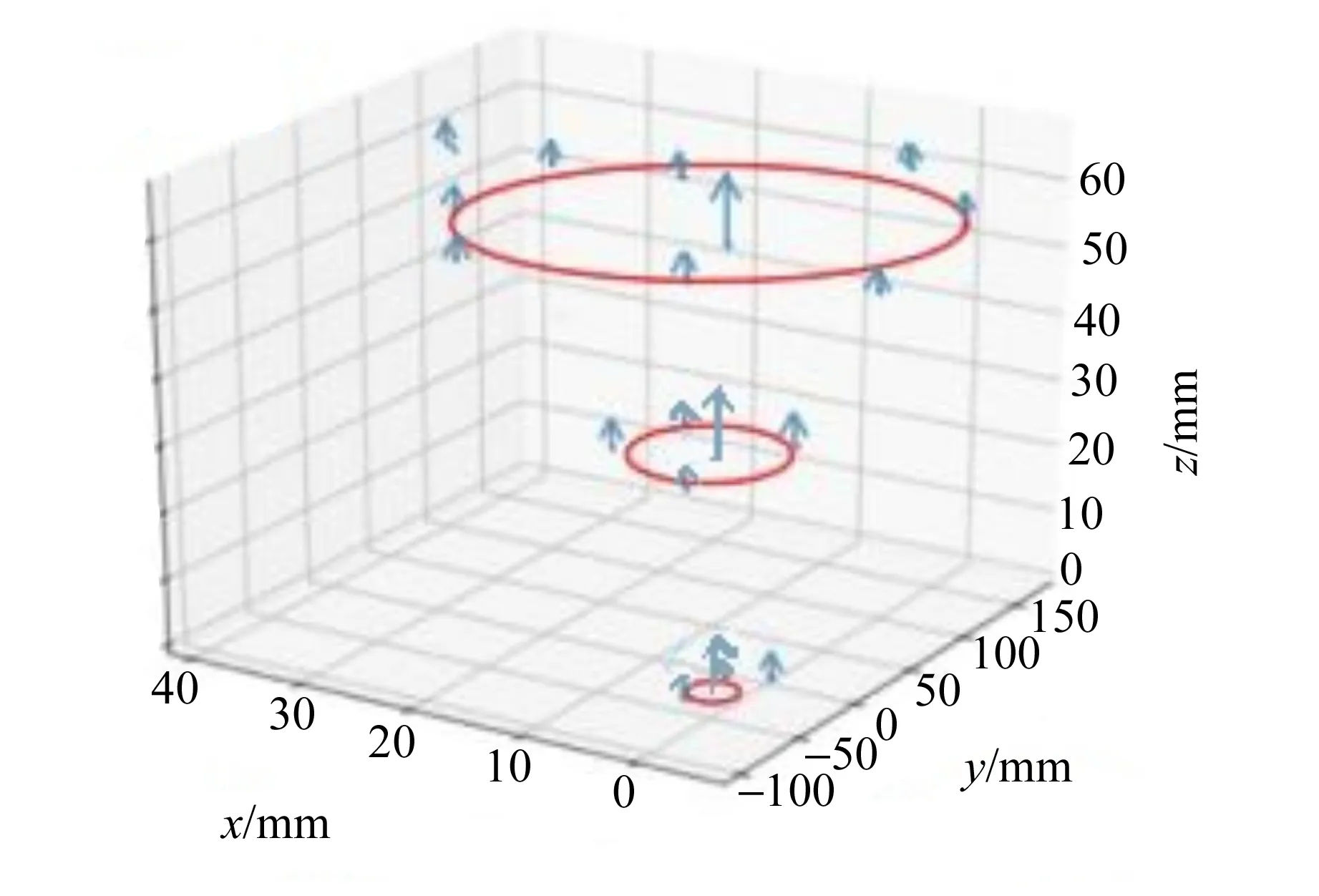
图12 涡量场

图13 黏度

6 结 论

利用Autodesk CFD软件对实验参量进行模拟，探究了横流和射流的流速比以及射水口的位置对实验的影响，并且最终确定当射水口的位置接近水面，横流速度为0.05 m/s，射流速度为8.00 m/s时的能产生巨大稳定的涡旋. 使用PVC材料搭建了尺寸为800 mm×300 mm×400 mm实验装置，利用射流冲击横流的原理产生涡旋，并在3D-PIV技术的基础上设计算法测量涡旋的三维结构，测量出涡旋的速度环量场、线速度场、涡量场以及黏度，分析发现速度环量场、涡量场符合理论和实际实验的情况，线速度与速度环量场结果一致，测得粒子的平均黏度为0.898 2 mm2·s-1，与水的标准值1 mm2·s-1大致相同.