转管武器机芯主滚轮滚动特性动力学分析
王海旭,张鹏军,杨一帆,余朝发
(1.中北大学 机电工程学院, 太原 030051; 2.陆军工程大学军械士官学校, 武汉 430000)
转管武器凸轮曲线槽主滚轮系统是一种典型的高速重载反圆柱凸轮系统,机芯运动加速度可达2 000~6 000 m/s2,速度可达10~30 m/s,且在极短的自动循环时间内存在供弹、开闭锁等复杂的受力状态[1]。机芯滚轮可以降低机芯与曲线槽之间的摩擦力,减少机芯与曲线槽之间的磨损。转管武器大多使用圆柱滚轮,这种滚轮在曲线槽中绕自身轴自由回转时,滚轮与曲线槽之间必须保证一定的间隙,间隙的存在会造成滚轮缺乏完善的约束,与曲线槽两侧交替接触,形成颤动现象,滚轮与曲线槽之间同时存在滚动和滑动运动[2]。此外,机芯运动状态改变时,因间隙的存在,滚轮在曲线槽中会发生失去接触的现象,待再次接触时会产生碰撞,引起剧烈振动,并产生噪声。碰撞时速度、加速度和接触力可能是无间隙状态下的几倍或者几十倍,称之为横越冲击现象[3]。薄玉成、徐健[1,4]等就高速反圆柱凸轮机构滚轮纯滚动动力学进行了分析,根据对凸轮体角加速度的判断和分析得到凸轮的运动状态,为尽量避免凸轮在运动过程中出现短暂非滚动状态提供了有效的解决途径。竺志超[5]等人研究了凸轮机构中滚子的纯滚动问题,导出滚子纯滚动的动力学条件,并以此为基础分析了机构结构参数、转速、外载、摩擦等对滚子纯滚动的影响关系。何雪明、张超洋[3,6]对横越冲击现象进行了动力学仿真和理论分析,并提出了防止横越冲击现象的方法。
文献[1]和文献[4]中对高速圆柱凸轮纯滚动条件的研究并没有考虑圆柱凸轮双面约束的特点,机芯开始减速运动时,机芯滚轮从一个约束面向另一个约束面横越运动,受力方向发生变化,滚轮运动是先减速运动,然后反向转动,文献[1]和文献[4]中忽略了这一特性,因此所给出的纯滚动条件具有一定的局限性。
通过对机芯滚轮运动特性进行理论计算与仿真分析,研究了机芯滚轮与曲线槽之间的力学关系,分析了转管武器机芯滚轮在曲线槽滚动和滑动的区域,以及机芯主滚轮的转速和角加速度变化规律。为转管武器凸轮结构优化设计提供依据。
1 机芯滚轮滚/滑运动分析
1.1 机芯主滚轮受力分析[7]
为方便受力分析,现将机芯简化,简化模型如图1所示。

图1 机芯简化模型示意图
参考文献[4]可得,机芯组件受力分析如图2所示,其中Fa为机芯轴向运动时受到的惯性力,Rfr、Rfc、Rfα分别为机芯翻转力造成的摩擦力、离心力造成的轴向摩擦力、启动加速度造成的径向力,N为滚轮与曲线槽法相正压力,Nτ为垂直机芯运动方向的推力,Nf为机芯运动方向的推力,β为曲线槽压力角,μr为机芯滚轮滚动时静滑动摩擦系数。可以看出,当约束面发生变化,摩擦力Nμr的方向不变,由于相对于滚轮的作用点发生变化,其对滚轮的转动力矩方向也发生改变。

图2 机芯组件受力分析
1.2 机芯滚轮滚/滑运动分析[1,4-5]
机芯主滚轮在曲线槽内的运动主要是滚动,在主滚轮纯滚动时,主要受到法向正压力N和静摩擦力Ff,相比法向正压力N和静摩擦力Ff,来自销轴的约束力是高阶小量,本研究中认为可以略去。机芯滚轮速度分解如图3所示。

图3 机芯滚轮速度分解
图中,vf为机芯滚轮速度的轴向分量,vt为机芯滚轮速度的周向分量。参考文献[8]中可得,机芯滚轮为纯滚动时:
(1)
(2)
式中:a为机芯轴向加速度;ω0为机芯滚轮转速;ε为滚轮角加速度。
当机芯由匀速段进入减速段,约束面改变,发生相对滑动摩擦时:
(3)
ω0=ω1-εt
(4)
式中:ω1为匀速段末滚轮转速。
第一,优化升级农村产业结构,大力发展农村特色产业。以市场需求为导向,立足当地自然环境条件、交通条件和特色农业,对农产品进行深加工,建立农产品生产、加工、销售一条龙发展路线,走产业化和集约化发展之路。第二,当地政府要对农民进行科学技术培训学习,提高农民的科学技术素养,鼓励农民在家创业就业[2]。因此,要改变传统农村经济发展模式,提高农村经济发展的质量和水平,实现农民就近就业和收入稳步增长。
2 数值计算与仿真分析
以某转管武器为例,其凸轮曲线槽为正弦加速度型,滚轮转动惯量J=1.587e-7 kg·m2,机芯中心回转半径R=32 mm,机芯组件质量Mb=0.35 kg,滚轮与曲线槽接触处摩擦因数μr=0.1,角速度ω=36 π/s。
经计算,滚轮与曲线槽法向正压力N的变化曲线如图4所示,压力方向由曲线槽指向滚轮,且定义当机芯轴线方向上的压力分量指向射击方向时,法向正压力为负值。
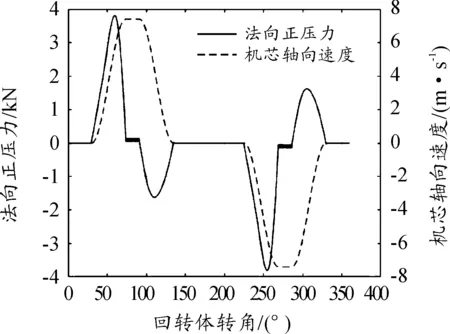
图4 机芯滚轮与曲线槽法向正压力变化曲线
由图4可以看出,机芯运动由匀速段进入减速段时,法向正压力N跨越0值,方向改变,此时,机芯发生横越现象,曲线槽对滚轮的约束面发生变化,由图2所示曲线槽不同约束面与滚轮的接触关系可以看出,滚轮受到与转动方向相反的力,此时,滚轮与曲线槽间发生相对滑动。
为滚轮运动时所受静摩擦力Ff和理论最大静摩擦力Nμr的变化曲线如图5所示,对比图4速度曲线可以看出,在非减速段,Nμr值远大于Ff,由式(3)可知,在这些区段内,滚轮能够实现纯滚动。当滚轮进入曲线槽减速段,滚轮与曲线槽发生相对滑动,滚轮受到的摩擦力值等于最大静摩擦力。

图5 静摩擦力Ff和理论最大静摩擦力Nμr
根据上述分析,结合现有曲线槽基本结构,运用Matlab软件编程计算出滚轮运动速度和加速度,如图6、图7所示。图6为机芯滚轮角加速度变化曲线,图7为机芯滚轮角速度变化曲线。在减速段前段,滑动摩擦力与滚轮旋转方向相反,存在一个迅速增大的角加速度。图7所示滚轮角速度曲线可知,滚轮转速迅速下降并反向旋转,直到达到反向旋转时的纯滚动条件。
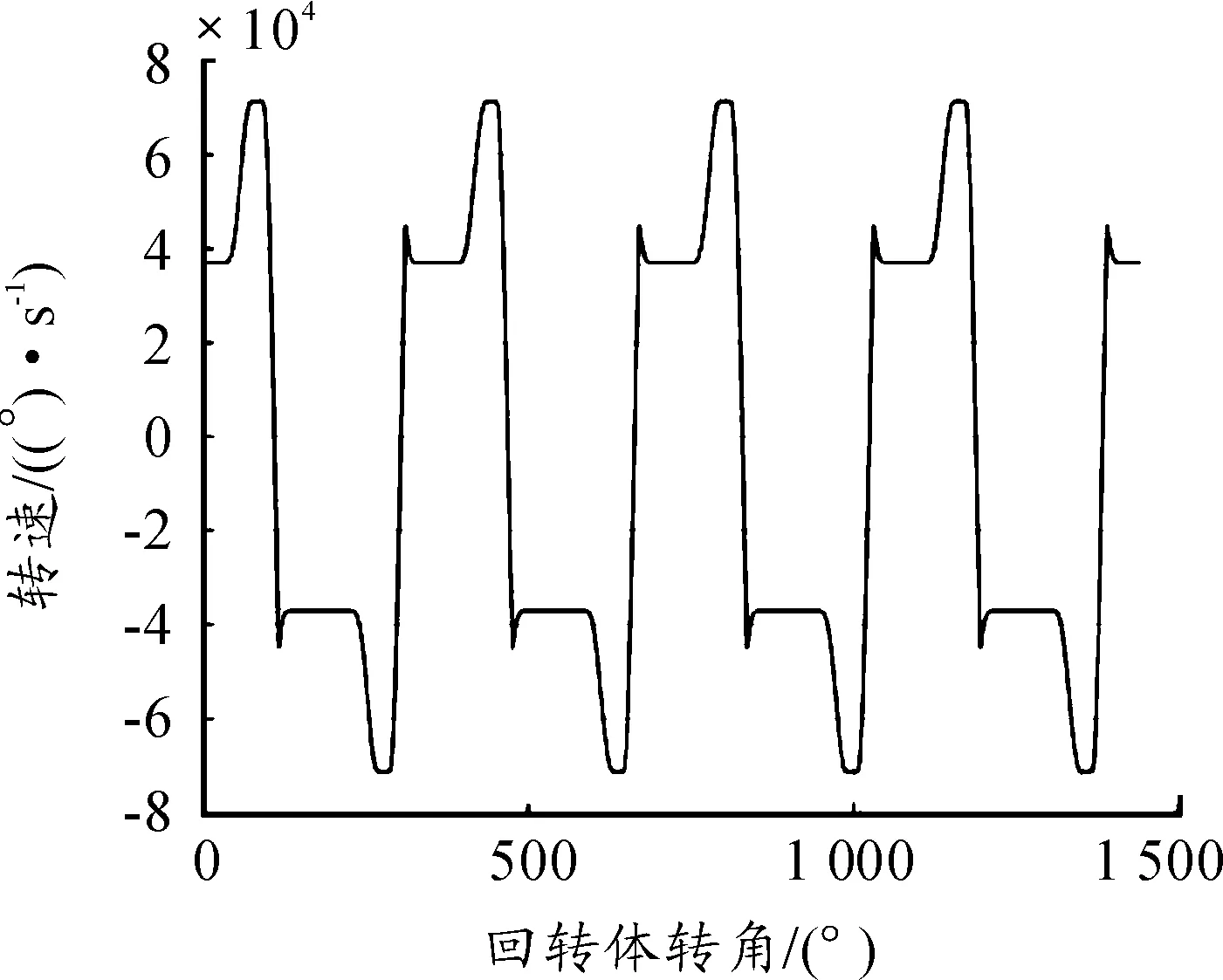
图7 机芯滚轮角速度曲线
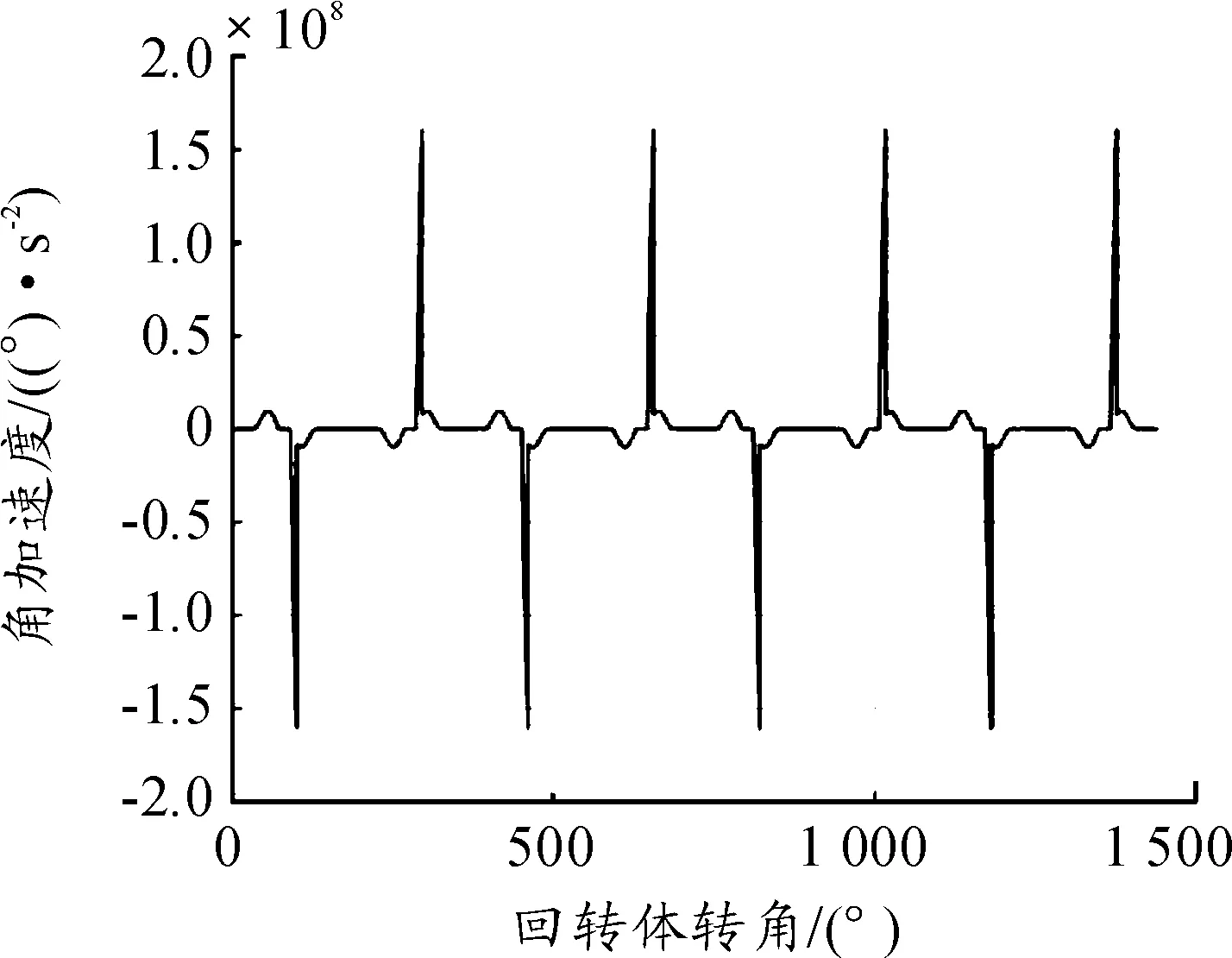
图6 机芯滚轮角加速度曲线
为了验证上述计算结果的准确性,通过Matlab构造转管武器曲线槽轮廓线,并将数据点导入UG软件,建立自动机曲线槽模型,然后将带有曲线槽的自动机虚拟样机模型导入Adams软件进行动力学仿真。机芯部件的约束关系模型、自动机虚拟样机模型,分别如图8、图9所示。

图9 自动机虚拟样机模型

图8 机芯部件约束关系模型框图
机芯滚轮角加速度和角速度变化情况的仿真结果分别如图10、图11所示。数值计算与动力学仿真结果对比分析如表1所示,机芯滚轮角速度与角加速度相对误差分别为3.26%、4.16%,两者基本相符。
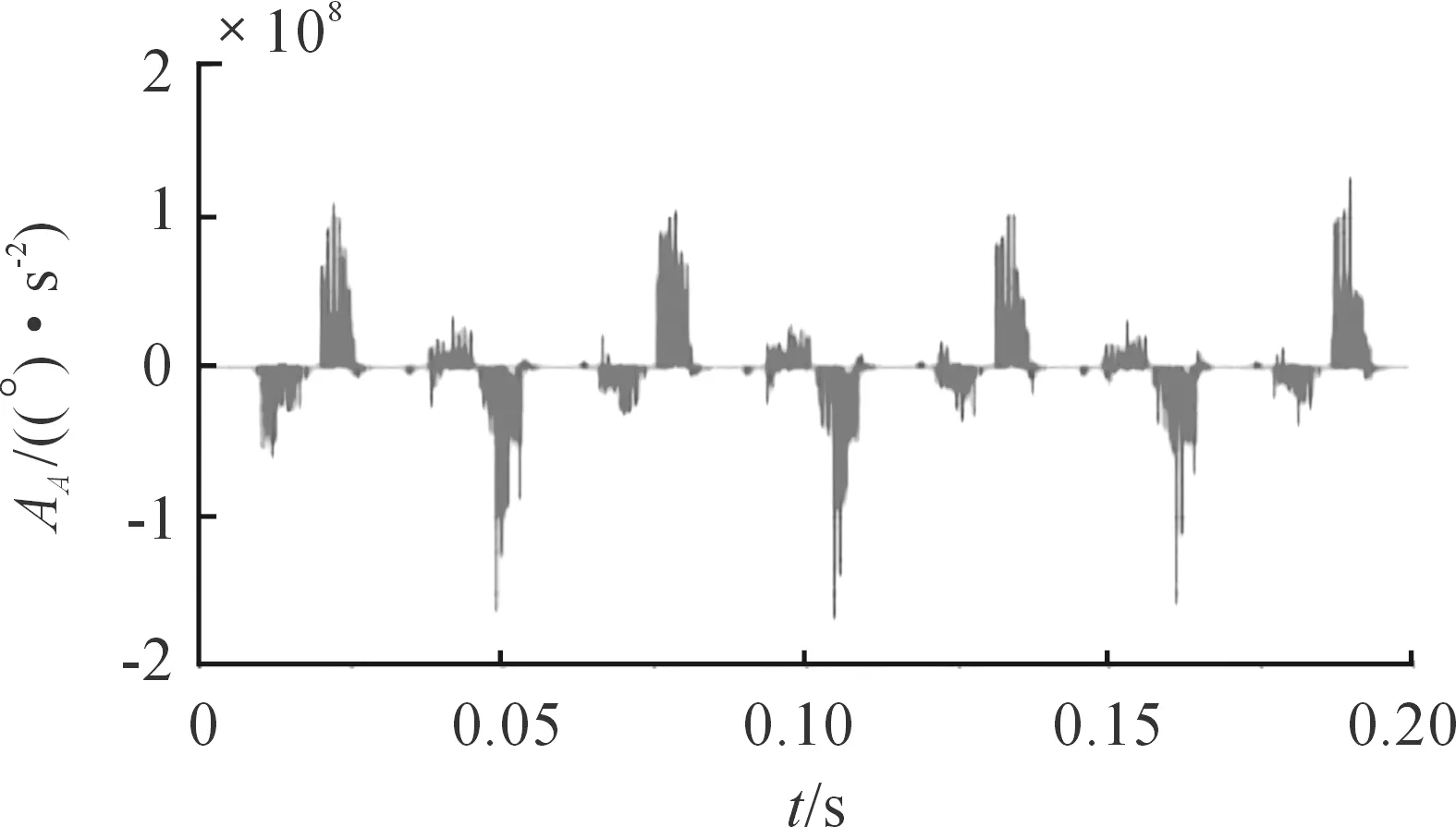
图10 机芯滚轮角加速度仿真曲线
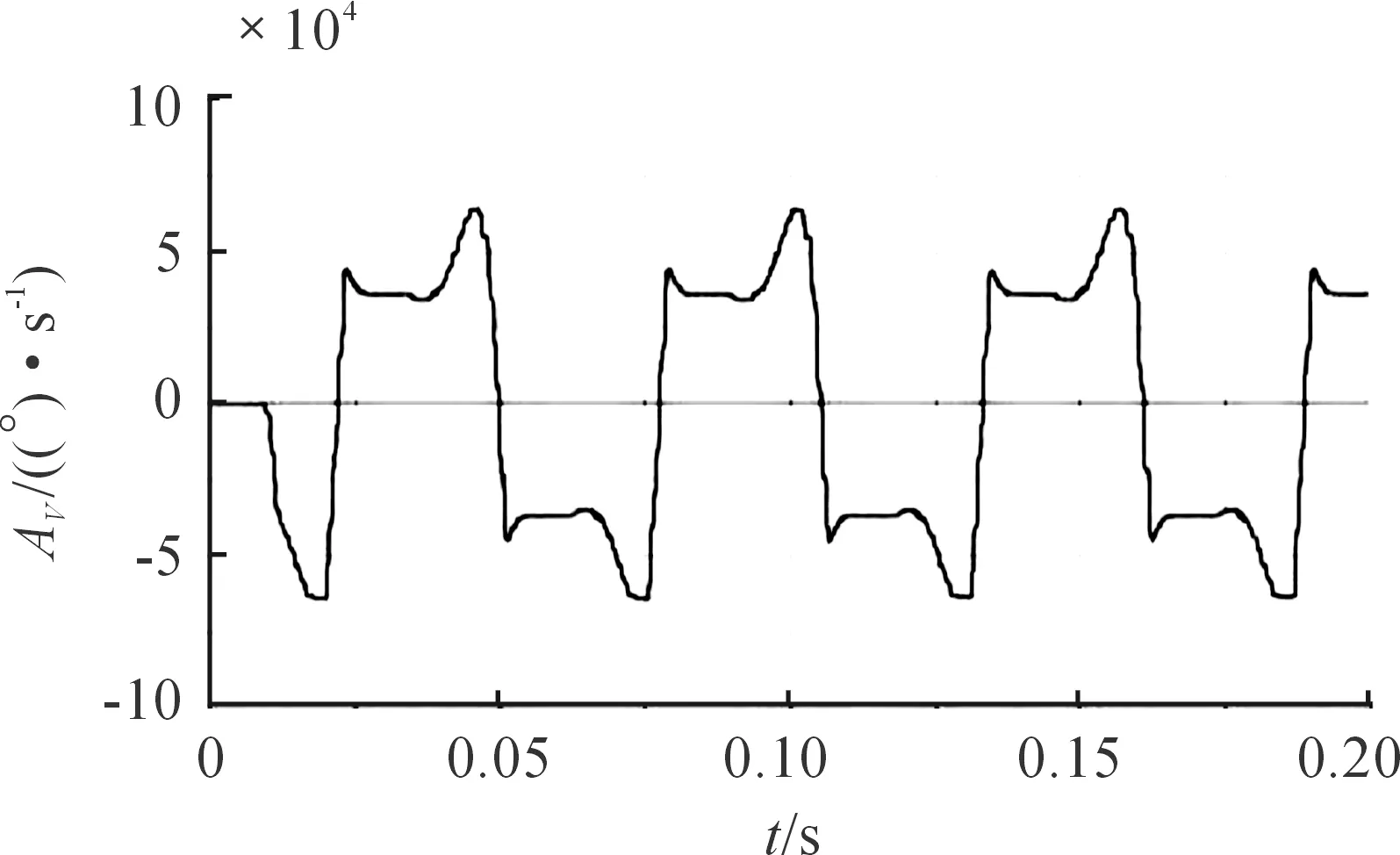
图11 机芯滚轮角速度仿真曲线
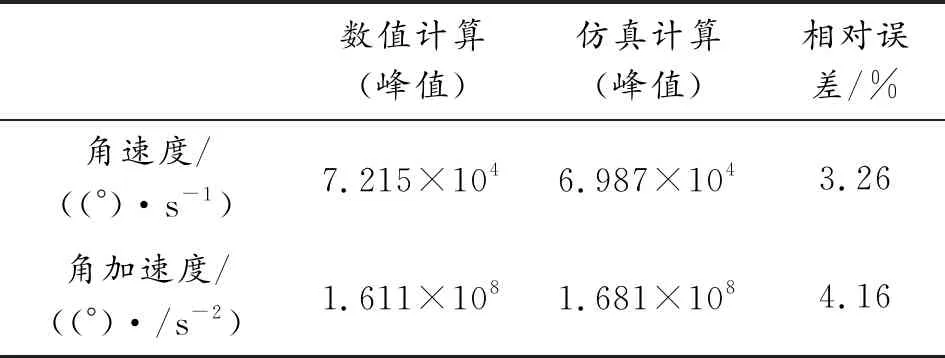
表1 数值计算与动力学仿真结果
根据仿真结果得出机芯滚轮在曲线槽内的滚动与滑动分布情况,如图12所示。
根据上述仿真结果可知,机芯滚轮离开后直线段后进入过渡段,在过渡段与斜直线段,滚轮与曲线槽后约束面接触,在这一阶段,机芯滚轮能够实现纯滚动。
当机芯运动到横越点,机芯滚轮约束面由后约束面变成前约束面,摩擦力方向与滚轮转动方向相反,机芯滚轮与曲线槽发生相对滑动,故此区域为滑动区。
在滑动区内,机芯滚轮角速度减小,当滚轮角速度下降为零,由于摩擦力的作用,滚轮反向旋转,此时,滚轮与曲线槽间存在滚动与滑动两种状态,故此区域为混合区。
如果有足够大的摩擦系数,滚轮经过滑动区和混合区,将会在当前过渡段内再次实现纯滚动;但如果当前过渡段内的摩擦系数很小,不足以使滚轮反向实现纯滚动,当前过渡段将只存在滑动区和混合区。
对于圆柱滚子凸轮,为了使滚子旋转,曲线槽与滚子之间必须有足够的间隙,在前直线段内,机芯不受轴向压力,但击发时的振动激励会使滚轮在曲线槽内振动,与两个约束面交替接触,出现转速的波动[3]。
当滚轮离开前直线段,机芯向后运动,由于开锁提供的较大轴向力,滚轮能在过渡段内实现纯滚动,在机芯向后运动过程中,滚轮将会重复上述过程。
3 结论
1) 机芯滚轮与曲线槽的法向正压力最大值出现在过渡段中部,适当增加过渡段摩擦因数,有利于减小滑动区与混合区宽度。
2) 转管武器凸轮结构优化设计时,应在较小压力处形成滑动或混合运动而在较大压力处实现纯滚动,有利于减小重载处的磨损,增加曲线槽的使用寿命。

