完全共享客户配送任务的供应商协同配送研究

金建靖，李益兵

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.武汉理工大学 湖北省数字制造重点实验室，湖北 武汉 430070)

协同配送作为近些年发展和积极实施的现代配送模式，是一种有效促进配送一体化的方法之一。它改善了原有独立配送的分散、低效和重复状况，在提高配送效率，减少配送成本，降低环境污染上卓有成效，因此成为了众多从业者和学者们关注和研究的焦点。

协同配送研究的一个重点是多配送中心的车辆路径规划问题。Wang等[1]提出了一种多中心协同车辆路径选择问题，该问题采用多中心协同的方式，实现了网络中车辆数量和运行成本的最小化。马云鹤[2]考虑存在充电续驶里程限制的基于电动物流车的多物流中心协同配送路径问题模型。廖伟等[3]针对客户需求不能被所有配送中心满足的情况，建立考虑客户需求差异性的多配送中心车辆路径优化模型。肖玉徽等[4]研究了多个配送中心协同配送下的车辆路径问题，建立了运力和时间窗约束下的成本最小化模型。针对拥有多个配送中心运力不均的情况，鲍春玲等[5]提出了一种考虑时间窗、碳排放成本和货损成本的多配送中心冷链物流配送路径优化问题。上述研究丰富了协同配送的研究成果，但没有充分研究考虑供应商在协同配送时为进行货物的委托必要的货物转交过程。因此笔者面向中小型供应商，提出完全共享客户配送任务的供应商协同配送模型，并考虑供应商的货物转交过程。设计了混合算法对模型进行分阶段求解，并通过算例对模型及算法的有效性进行了验证。

1 问题描述

完全共享客户配送任务的供应商协同配送是指供应商可以将配送任务委托给其他任意供应商[6-7]。协作时，供应商需要设法将货物进行转交给被委托供应商，常见委托方式主要有原地收货、沿途取货、集中取换货。为最小化行驶距离，采用集中取换货的货物转交方式。

完全共享客户下的供应商协同配送需要解决两个问题：

(1)供应商之间的配送任务重组。主要解决在满足各供应商运载能力约束和客户需求约束下的所有客户配送任务在不同供应商间分配的问题。

(2)路径规划问题。确定配送任务重组方案后，需要解决以下问题：①选取其中一个供应商(仓库)作为所有供应商的集货点，以便其他供应商先前往该集货点进行货物交换；②规划供应商从集货点出发前往相应的客户配送的路径[8-9]。

1.1 条件及假设

已知条件：客户对各供应商的货物需求，包括重量和体积；各供应商与客户的地理位置、最短行驶距离均已知；各供应商的车辆额定载重和体积。

假设条件：一旦供应商将某客户的配送任务委托给其他供应商，则订单下的货物全部被转交；各供应商配送车辆从仓库出发，最终回到原仓库；供应商载荷不能超过其配送车能力；无客户配送时间窗限制；各供应商车辆在取货阶段行驶速度相同。

文中涉及的符号及意义如表1所示。

表1 符号说明

1.2 目标与约束

目标为协同配送总距离最小，如式(1)所示：

(1)

约束条件为：

(2)

(3)

(4)

∀j,k≠i,r∈R

(5)

k≠i,r∈R

(6)

(7)

(8)

2 混合算法设计

笔者设计的混合求解算法为：改进的差分进化算法(differential evolution，DE)解决供应商之间的配送任务重组问题；类重心法确定作为集货点的供应商；经典蚁群算法(ant colony algorithm，ACO)求解各供应商最短配送路线。

2.1 改进的差分进化算法设计

2.1.1 编码方案

每一代种群中均有Z个个体，每个个体由n个m×1的列向量构成。一个个体表示一个完整的由m个供应商针对n个客户的任务分配方案。Xg,i表示第g代的第i个个体。对于第g代的第i个个体的第j个(j=1，2，…，n)列向量xg,i,j，表示针对第j个客户的供应商之间的合作方案。列向量每一行的值为0到m，同时辅以下标表示包含的供应商编号。

2.1.2 变异

(1)生成客户的供应商合作行向量。对于客户j(1≤j≤n)，其供应商合作行向量为Cj=[c1,…,cL,…,cm]，m为供应商数量，其第L列的数值cL满足0≤cL≤m，数值cL表示L号供应商将给客户j的配送任务委托给供应商cL。但当供应商L不是客户j的服务供应商时，cL=0，只能接受委托。

(2)生成客户的供应商合作矩阵。行向量Cj映射为一个m×m带下标符号记录的0-1矩阵Cj_matrix。Cj第L列的数值cL映射到矩阵Cj_matrix中，对应第L列第cL行的值1，该列其他行为0。

(3)生成客户的供应商列向量。0-1矩阵Cj_matrix乘m×1的单位列向量P，得到新的客户供应商合作列向量Cj_new。新的列向量将替代原个体Xg,i中对应客户的供应商列向量xg,i,2。对一个个体的所有列向量执行变异和概率替换操作后，得到新的个体Xg,im。

2.1.3 交叉

由变异得到的包含新的个体，与原父代个体在相应客户的供应商合作列向量随机交叉，组合形成新个体。交叉系数CR=0.5，r为0～1间的随机数。当r≥CR，xg,ic,j=xg,i,j；否则，xg,ic,j=xg,im,j。

2.2 类重心法

采用类重心法快速选取一名供应商作为取换货的集货点。[10]该方法将各客户及供应商看成是分布在某一平面物流系统内的已知点，各客户的需求总量，各供应商的配送总量分别看作物体的重量，选取重心使系统其他各点至重心的“距离×运输量”之和最小。当选取供应商si作为重心时，计算公式为Tsi=∑r∈Rwrdrsi+∑s∈Ssiwsdssi。因此，选取作为集货点供应商s0，满足s0={s|s0∈min[Tsi],si∈S}。

2.3 蚁群算法

蚁群算法是一种群体智能启发式优化方法，在求解单车辆路径问题时具有较高的求解效率。因此笔者用蚁群算法规划供应商从集货点前往各客户并返回原点的最短路径。

算法步骤如下：

霍克海默、阿多诺以及黑格尔对于启蒙理性的分析对于我们深入思考改革开放以来所出现的问题具有一定的启发意义。

(1)根据待优化路线的客户数量，初始化蚂蚁数量nant，最大迭代次数Gen，信息素重要程度α，启发式因子重要程度β，信息素蒸发系数ρ(0<ρ≤1)，信息素增强系数Q，循环次数gen。

(2)初始化各条路径的信息素含量，其初始值为Pheij=1/dij。根据求解的要求，对部分节点间距离采用非对称设计，以保证蚂蚁的搜索方向符合“集货点-客户-配送供应商原点”访问顺序限定，设定ds0s=1010，dss0=1010，drcis0=1010，dsrci=1010。

(3)设定供应商集货点为初始节点，配送供应商为终止节点，将nant只蚂蚁都放置在初始节点上，各蚂蚁以初始节点为中心，搜索下一个移动的客户节点。

(4)初始化禁忌表。将配送集货点放置在禁忌表tabu_list第一位。

(6)计算每只蚂蚁的路径长度，将本次循环中总长度最小的路径作为最优解。

(8)当gen=Gen，循环结束，得到最短路径；否则，清空禁忌表，转至(4)。

3 实例分析

通过选取江苏省某市区10个坐落于市内的供应商S1-S10，20家位于乡镇的客户R1-R20进行配送研究。表2为独立配送和协同配送的效果对比。从表2可知，协同配送模式下，不同供应商针对相同客户的配送任务，均被有效地重组整合，最终由一个供应商来完成配送，由此减少供应商的配送里程和需要访问的站点数量。其中，总行驶距离为546.26 km，对比传统独立配送总距离1 036.12 km，下降了489.86 km(47.28%)。同时，各供应商的行驶距离均有明显下降(13.5%～79.5%)。在供应商路线站点数量上，协同配送增加了9个供应商站点，但总客户站点数量之和由63个站点减少到20个站点，减少约2/3。因此，总站点数量下降了34个，超过1/2。

综上分析，说明该协同配送模式能有效整合配送需求，减少配送站点数量及里程。

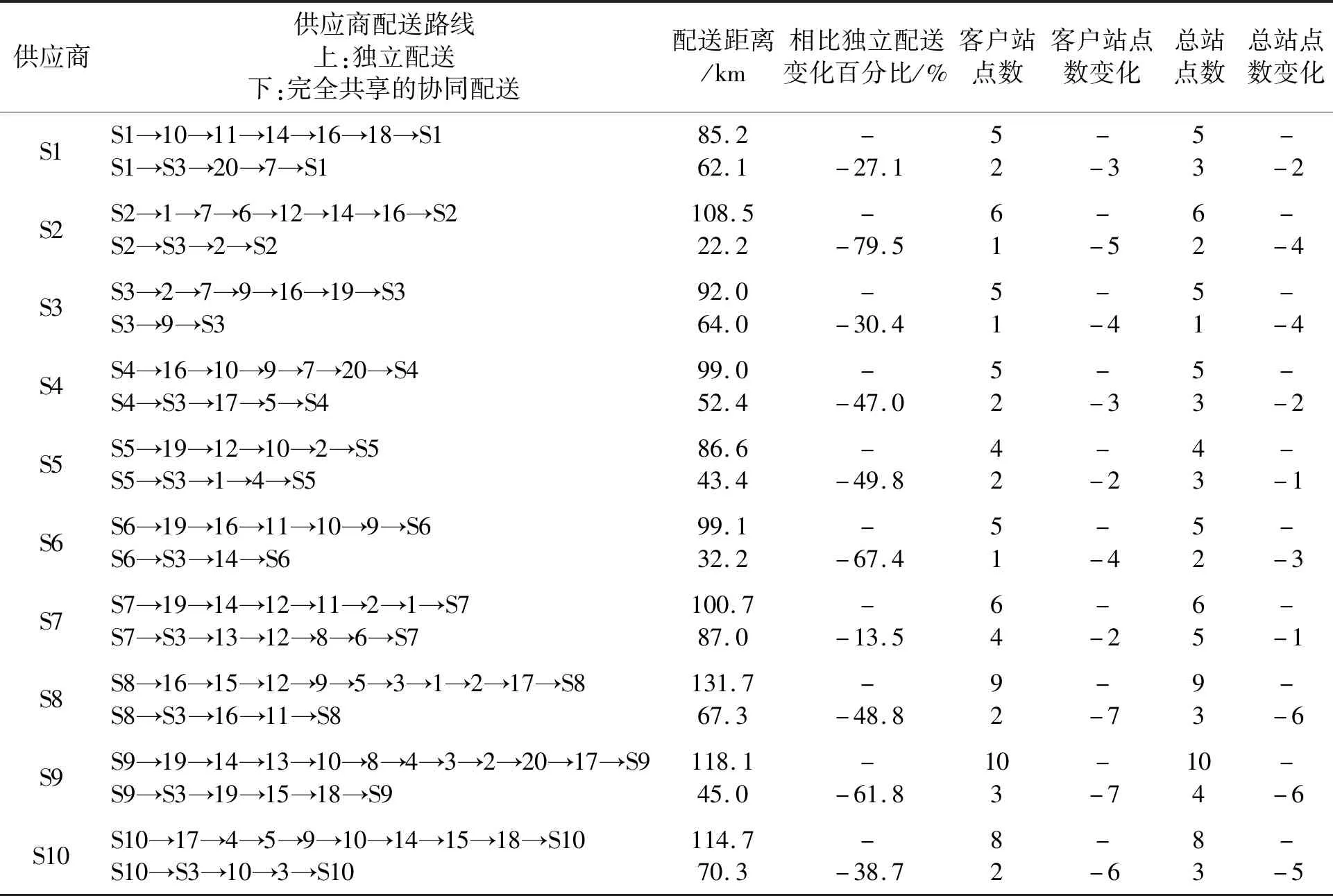
表2 最优解下各供应商的协同配送路线与独立配送对比

4 结论

在满足供应商运输能力约束和客户订单约束的条件下，建立完全共享配送任务的供应商协同配送模型，通过改进的差分进化算法，类重心法和蚁群算法的混合算法分别求解模型中的供应商组合问题、集货点选取问题和路径规划问题，并通过模拟实验验证了模型及算法，结果表明对中小型供应商，采用协同配送能有效缩减供应商的配送里程，减少站点数量。在今后的研究中，可以将客户对供应商服务选择的偏好、满意度等评价指标考虑到供应商的委托组合中，从客户的角度提高协同配送的质量。