考虑工件运输时间的绿色柔性作业车间调度研究

李香怡，何星月，王 磊，唐红涛

(1.武汉理工大学 机电工程学院，湖北 武汉 430070;2.武汉市第十五中学，湖北 武汉 430000)

随着全球制造业快速发展，控制机器加工时消耗能源而产生的碳排量是企业提高制造效率和行业竞争力重要手段[1]。

近年来，针对绿色柔性作业车间调度问题国内外学者展开了大量的研究。例如，赵宁等[2]基于领域搜索法提出了考虑运输时间的关键链法，以解决柔性车间调度问题。张国辉[3]在低碳策略下研究柔性车间调度安排，通过采用加工参数与调度方案同步方法构建优化调度模型。雷德明等[4]提出一种改进的帝国竞争算法用于求解低碳效应下并行机调度问题的多目标可行解。Xiang等[5]提出了一种分期界定算法用于解决考虑释放时间的柔性作业车间调度问题。姜天华[6]建立了以加工能耗和加工时间最小为目标的低碳车间调度模型，并将灰狼算法进行改进优化，以提高算法的局部搜索能力。蒋增强等[7]考虑能耗、最大完工时间、成本、质量等目标，建立了多目标柔性作业车间绿色优化调度模型，设计了基于血缘变异的混合非支配排序遗传算法进行求解。上述研究虽然有效解决了柔性作业车间绿色调度问题，然而随着制造水平的提高， AGV、生产机器人等先进的高智能作业设备逐步成为车间调度研究的新的方向和目标[8]。

笔者以低碳策略为核心，考虑生产实际中的因物料搬运对调度方案产生的影响，建立柔性车间调度模型。采用改进的粒子群算法，对种群基因前、后两段分别采用POX、RPX交叉方式，提高全局搜索能力，最后结合某柔性作业车间的生产实际案例对算法的可行性和优越性进行证明。

1 问题描述及数学模型

1.1 问题描述

在加工车间中，任意工件都需要经过若干道工序的加工，每一道工序都有相对应的候选机器集合，同时每台机器可以有序地加工多种工序，这样多对多的关系就产生了多种不同的工序-加工机器调度安排。结合不同生产实际的要求，使所有加工机器按照一定顺序加工最适合的工序，以满足不同的生产需求。

1.2 数学模型描述

基本变量和参数进行如下定义：i为工件序号，i=1,2,…,n，其中n为工件个数；j为工序序号，j=1,2,…,p，其中p为工件i对应的工序数；h为机器序号，h=1,2,…,m，其中m为机器总数。

1.2.1 决策变量

决策变量定义如下：

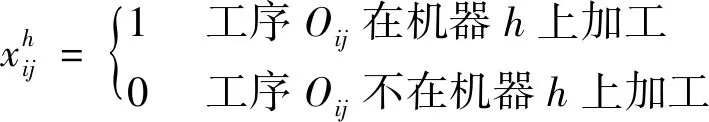
(1)

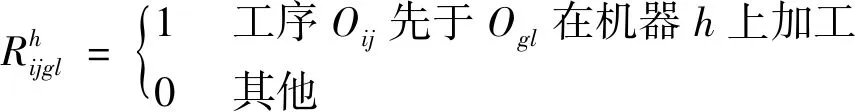
(2)

(3)

1.2.2 目标函数

(1)最小化最大完工时间。最大完工时间是指全部工件加工完成所需要的所有时间，减少最大完工时间可以使整个调度周期缩短。

minCmax=min(max{Ci|i=1,2,…,n})

(4)

式中：Cmax为最大完工时间；Ci为工件i的加工完成时间，以每一个工件的完成时间为计算对象来确定最大完工时间，其中：

(5)

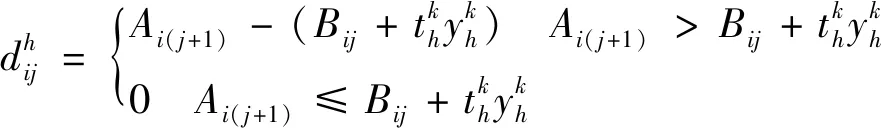
(6)

式中:Ai(j+1)表示工序Oij下一道工序的开始时间；Bij为工序Oij的结束时间。

计算每个工件的完工时间时，只需考虑工件等待时间，无需考虑机器等待时间。

(2)总排碳量最小。文中只考虑了机器加工过程中消耗的电能所产生的碳排放，通过折标准煤系数和碳排放系数将电能转化为碳排放量。

ZM|i=1,2,…,n,j=1,2,…,p)

(7)

式中：ph为机器h加工时额定功率；EF为碳排放系数,可以将各种能源在生产过程中所消耗总量转化为对应的碳排量；ZM为折标准煤系数,可以将不同品种、不同含热量的能源折合成为统一标准含量的能源，文中采用的折标准煤系数为0.123 kgce/(kWh)。

(3)最大机器负荷最小。机器负荷指加工过程中每一个加工机器的净加工时间，最小化最大机器负荷可以平衡各个机器加工时间，提高机器的耐用度，wh为生产过程中的最大机器负荷。

(8)

2 基于改进粒子算法的模型求解

2.1 染色体编码、解码

染色体的编码方式对粒子群算法有直接的影响，为使算法可以更快运行求解同时保证算法的计算精度，采用两段式编码方式：前n维部分表示所有工件的工序排列。后n维表示对应工序进行加工时选择的机器集编号，具体编码方式如图1所示。

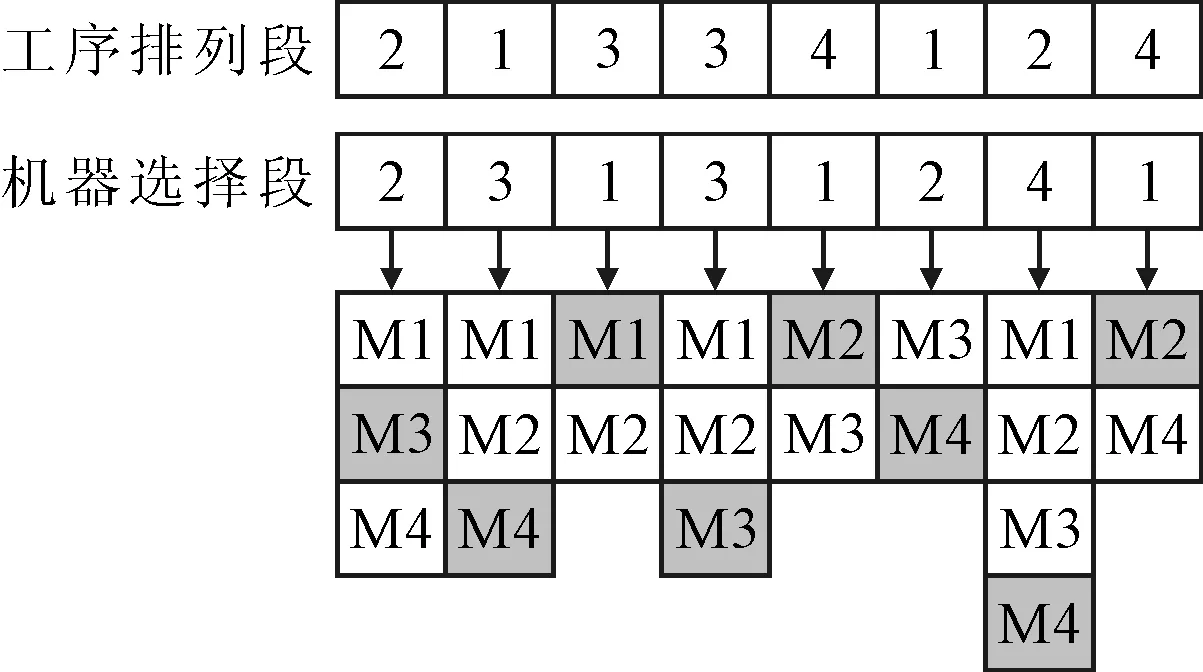
图1 基因编码方式

2.2 交叉操作

2.2.1 POX交叉规则

良好的交叉算子不仅可以使子代继承父代优良特性，还会提高子代种群多样性，使算法具有良好的全局收敛性。笔者在工序排列段采用基于工序解码POX[9]交叉算子，其交叉过程如下：

(1)随机选择若干个工件组成一个工件集G；

(2)将p1、p2中属于工件集G中的所有工序分别复制到c1、c2，同时保留它们的位置；

(3)将p1中不属于工件集G的所有工序按照其顺序复制到c2，p2中不属于工件集G的所有工序按照其顺序复制到c；交叉过程如图2所示。

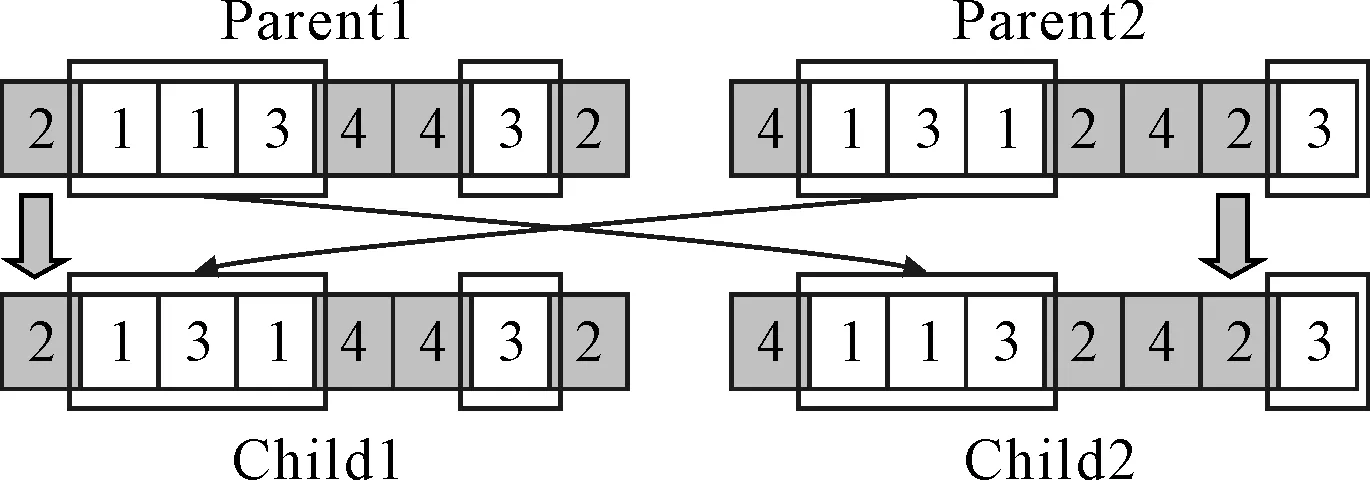
图2 POX交叉方式

2.2.2 RPX交叉规则

对资源选择段进行RPX交换[10]。首先随机产生在 [0,1]间的随机均匀值pf，标记父代p1中数值小于pf对应位置的工件工序，从p2的机器选择段中找出记录的p1中的工件工序对应的机器，并将其复制到子代中同时保留其位置，p1中未被记录的工件对应的机器按顺序放入子代中的剩余位置。如果假设pf=0.6，父代进行RPX交叉过程如图3所示。

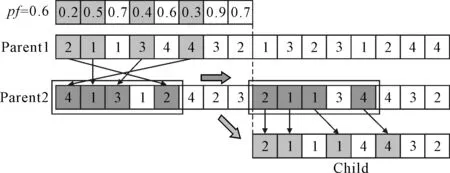
图3 RPX交叉方式

2.3 非支配排序

传统解决多目标问题方式多是将其转化为单目标问题，但是考虑到多个目标之间相互限制、矛盾，得出的唯一解并不一定适用，当前多目标问题最优解的选择主要采用非支配排序[11]。当对一种群进行多目标函数问题进行分层时，种群中每一个体都要与除自身以外的所有个体进行比较，每一轮对比都会找出当前种群中较为优良的个体并计入当前非支配层级，同时在下一轮比较将它们淘汰。通过不断比较，依次找到每一级非支配层中所有非支配个体，直到将所有个体分层。

3 案例应用与分析

3.1 案例描述

以某柔性作业车间为例，共有5个工件，并各有7道加工工序，车间内有11台加工机器可以进行加工作业，根据每个机器铭牌上的标注，每台机器工作的额定功率如表1所示。

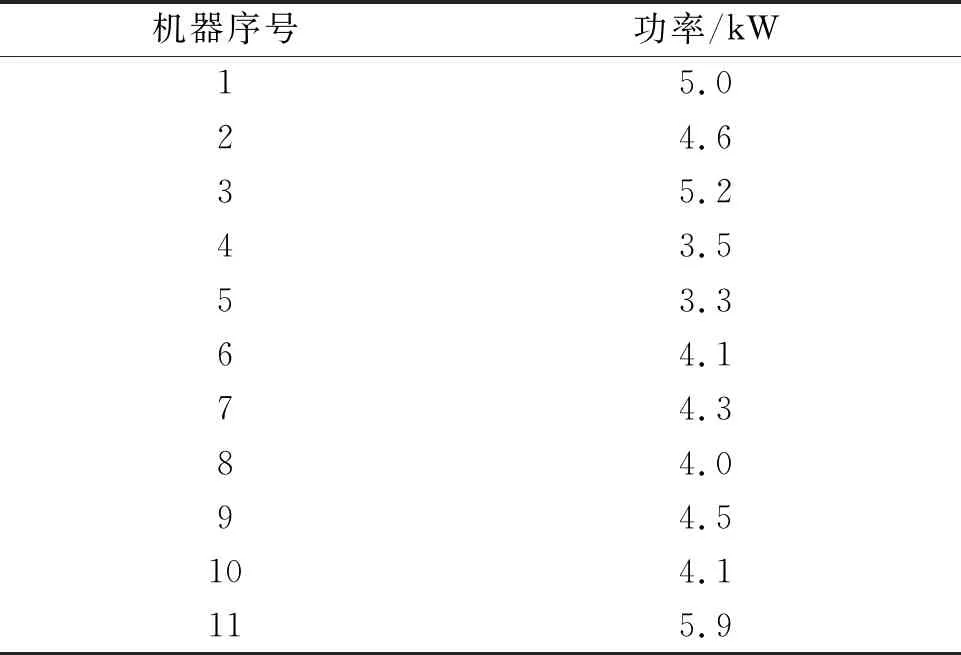
表1 每台机器工作的额定功率表

通过对加工过程中实际生产数据进行测量、简化和筛选之后，得到各个工序对应的可选机器集和相应加工时间的信息表，如表2所示。

表2 某精加工生产企业实际生产信息表

由于该企业车间设备规划问题，加工机器距离较远，相比于工件的加工时间，运输时间不可以忽略。采用生产车间原有的运输设备运输，对加工机器之间实际运输时间经行测量，以小时为单位，测得运输设备在机器间运输大约在0～0.4 h之间，假设运输工具在两机器之间的来回运输时间相同。

3.2 案例求解分析

将改进的粒子群算法在实验实施条件为MATLAB R2016a on an Intel Core i5 2.30 GHz PC with 8.00 GB of memory中运行。选取初始种群个数为50，迭代100次进行运算。采用结合了POX、RPX交叉方式的多目标粒子群算法，从运算结果中取出一个分布在最优解空间内部的解再对其进行解码，其结果甘特图如图4所示。

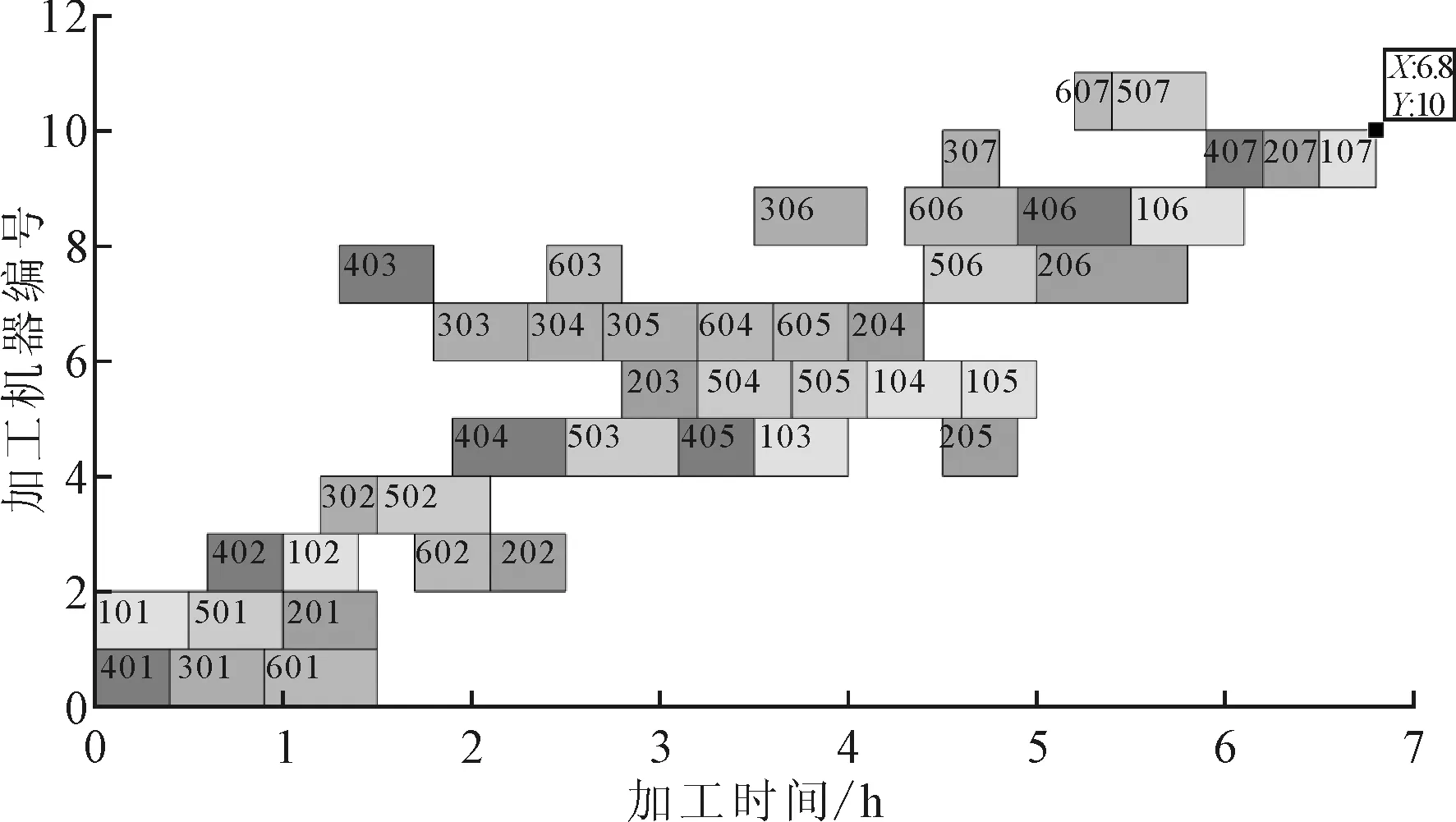
图4 改进粒子群算法调度甘特图

3.3 对比分析

将传统粒子群算法(multi-objective particle swarm optimization,MOPSO)、NSGA-II算法与改进粒子群算法运行结果进行对比，以验证算法有效性和优越性。由于元启发式算法每次运算都具有不确定性，参数的选取并不能保证是最优值，笔者采用正交实验设计法，通过多次实验组合选取最优参数，结果如表3所示。

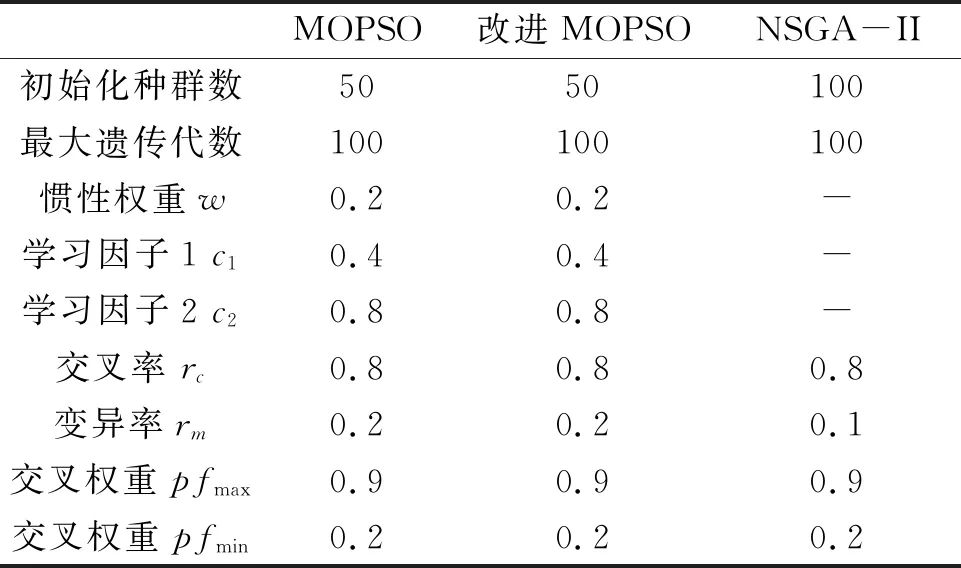
表3 MOPSO、改进MOPSO、NSGA-II设置参数

为减少算法运行中的偶然误差，对数据结果分析产生影响，将企业生产数据实例用3种算法重复运行10次，记录运行得到的Pareto第一前沿解集，通过算法绘制得到在各算法运行第一前沿解的分布三维分布图以及每两个目标相对应的二维分布图，如图5所示。图5中的坐标轴分别表示优化目标，坐标系中的粒子坐标则表示Pareto第一前沿解对应的目标函数值。

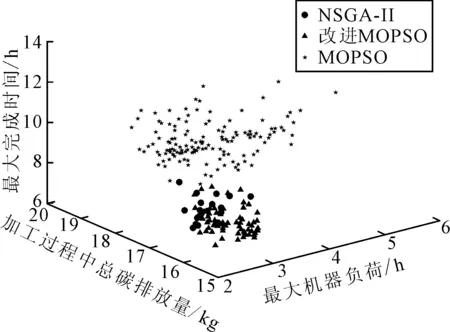
图5 Pareto第一前沿解的三维分布图

根据所得的Pareto第一前沿解三维分布，可看出采用POX和RPX交叉的粒子群算法所得的解的集合分布在三维坐标更靠近坐标原点的位置，说明改进的粒子群算法相较于其他两种算法运行结果更小，更加满足文中设置的3个最小化目标的要求。同时记录3种算法迭代过程中各个目标函数值的变化过程，绘制连续数据变化，结果如图6所示。

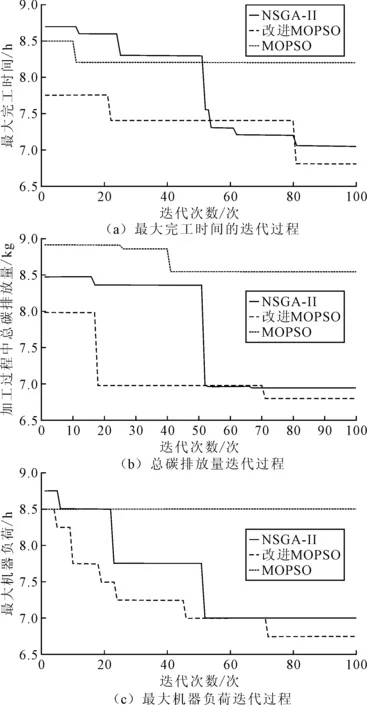
图6 不同算法的目标函数值变化过程

根据图6可知，采用的改进粒子群算法的各个目标函数值都可快速收敛于最优解，由于针对基因编码特点而运用两种不同的交叉方式，不仅保留父代的优良基因，还保证了种群个体的多样性，提高全局搜索能力，更易跳出局部最优陷阱同时收敛于最优解。

4 结论

笔者在考虑工件在加工机器之间的运输时间的基础上，算法设计上采用POX、RPX两种交叉方式的粒子群算法，同时利用非支配排序对3个目标进行综合协调，保证最优种群个体的多样性。在今后的研究中可对碳排放的控制范围进一步扩大，从生产原材料的选择采购、运输过程中运输设备的选用以及机器运转速度对生产碳排放的影响，实现碳排放在生产中的全过程控制。同时在模型建立中引入机器学习、数据驱动的智能技术，将机器故障预测、订单插入融合进车间调度问题中，使调度方案更加具有现实意义。