一种更具稳健性的计数控制图
杨佳靓


摘要:统计过程控制(SPC)技术已被证明在许多工业应用中是重要的,控制图是统计过程控制中最重要的工具。本文针对计数数据设计了一种更稳健的控制图。它对用于监视的小的过程转移非常敏感。我们将新设计出的统计量与EWMA相结合,并在不同的受控长度下进行检验。比较并分析该统计量在不同参数下的表现,结果表明其对泊松分布下的数据监测效果良好,其监测速度能够更快。
Abstract: Statistical process control (SPC) techniques have been shown to be important in many industrial applications, and control charts are the most important tool for statistical process control. In this paper, a more robust control chart is designed for counting data. It is very sensitive to small process transitions for monitoring. We combined the newly designed statistics with EWMA and tested them at different controlled lengths. By comparing and analyzing the performance of this statistic under different parameters, the results show that it has a good monitoring effect on the data of poisson distribution, and its monitoring speed is faster.
關键词:计数数据;控制图;稳健性
Key words: count data;control chart;robust
中图分类号:N945.13 文献标识码:A 文章编号:1006-4311(2020)17-0232-03
0 引言
统计过程控制(SPC)已成为监控和测量过程或产品质量的重要技术。如何改进产品质量成为了学术界讨论的焦点。早在20世纪,休哈特(Shewhart)就提出了过程控制理论监测的工具——控制图。统计过程控制(SPC)中的控制图可划分为计量控制图与计数控制图两类。其中计量控制图包括X-bar-R图、X-bar-S图;计数控制图包括N图、P图、C图、U图。Shewhart最早提出的控制图是产品不合格率的P图。现如今很多控制图都针对于正态分布数据,但实际情况中的数据并不一定服从于正态分布,例如产品缺陷,单位时间内的排队人数。因此对于计数控制图的研究就显得尤为重要。早在之前,Sheu 和Lin[1](2003)提出了一般加权移动平均(GWMA)控制图,提高了 EWMA 图的检测能力。Khoo[2](2004)推出了泊松移动平均控制图,为 c-chart 提供了更好的选择,并提高了计数控制图的监测能力。Shey 和Chiu[3](2007)利用了一般加权移动平均(GWMA)控制图来检测泊松分布过程均值的持续变化,这种控制图称为PGWMA 控制图。本文利用PGWMA控制图的统计量进行改善优化,并根据受控运行长度(ARL0)找到其最优化的监测方案。Chakraborty[4](2017)设计了GWMA-TBE 图表,这种图表在检测非常小到中等的变化方面优于著名的EWMA 和Shewhart 图表。Lu[5](2017)设计了混合加权移动平均控制图,这种控制图在大参数下具有很强的稳健性。Niladri[6](2018)提出了时间加权控制图,并表示该控制图性能优于其他控制图。Saghir[7](2018)基于辅助变量和重复采样的EWMA 控制图,用于监控过程位置。本文设计的计数型控制图将会结合EWMA控制图设计出一种新的控制图给计数数据进行良好的检测。
1 计数控制图的优化设计
在设计C控制图的时候,人们假设统计量的分布是服从泊松分布的,其均值和方差都等于它服从分布的参数。首先我们来计算平均运行长度(ARL),平均运行长度(ARL)是一个公认的控制图性能度量。ARL是检测到过程移位之前所获得的期望样本数。假设控制线参数为k,抽样比例为r,工序中发生偏移为d,则
(1)
我们可以先设定一个初始的ARL0和抽样比例r,于是就可以得出控制线参数k的取值
(2)
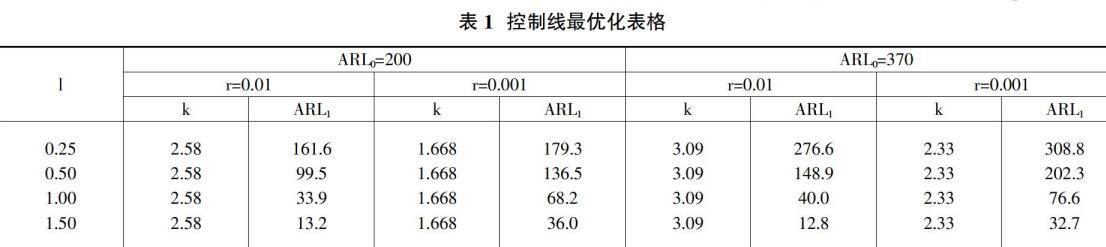
表1列出了在给定ARL0和抽样比例r,对于不同的偏移程度■,k的取值和ARL1的计算结果。根据表1我们可以得出,ARL0的增大导致ARL1的增大,r值的减小导致ARL1的减小。我们可以来用减小初始的ARL0和增大抽样比例r的方法来减小ARL1的值,增加控制图对偏移的灵敏程度。但是,ARL0的减小意味着错误报警率的增大,抽样比例r的增大意味着检验成本的增加,因此这两个参数的调整要根据实际工序的情况做出。而这里设计方案与前面讨论的计量控制图设计的不同在于,控制线参数k只根据ARL0和抽样比例r来决定,和偏移的大小无关。该方案对于比较大的偏移是敏感的,而对较小的波动较难发现,所以我们这种方法比较适合对大波动进行监控,而对于小波动,则应该结合EWMA图来进行探测和分析。
2 计数控制图的稳健性设计
本文介绍了一种用于监测计数数据的EWMA控制图,并分析了一系列监视流程的计数数据的方法。所研究的所有案例均涉及泊松EWMA控制图的变化。假设在时刻k采集相互独立且服从泊松分布的样本Xk1,Xk2,Xk3,Xk4…Xkn,k=1,2,3...,n为样本大小。本文通过对PGWMA的优化得到一种新的统计量
t=1,2,3…(3)
其中Y0和Z0取决于对象均值?滋0,?滋0是过程均值。其中权重因子■。q,a是控制图的参数。
通过结合Yt和Zt,可以得到一个更简便的式子
t=1,2,3…(4)
其中■。
3 表现评估
通过MATLAB仿真系统进行仿真。受控长度(ARL0) 是当过程处于控制状态时,检测到在失控状态之前获得的预期样本数。失控长度(ARL1)在过程平均移位后检测到在失控条件下获得的预期样本数。为了进一步了解此控制图的性能,以泊松分布为例,把受控长度(ARL0)分别设置为ARL0=200,370,500。并列出表现结果。
从表2可以得出,这个过程意味着在从?滋0=4移到?滋0=12(小的向上移动)。模拟了100次?滋0=4的连续泊松观测,取其结果均值并在表2中列出。表2展示了不同類型,参数q=0.7、0.8,a=0.5、0.6、0.7、0.8,和ARL0=200。在这个图表中,计数数据控制图检测到一个失控的信号远早于其他图表。
从表2、表3、表4的对比中可以得到当受控长度(ARL0)越小,检测的速度就会越高,但ARL0越小,受控状态下的错误报警率就会越高。在实际生产过程中可根据自身需要调节ARL0的大小。当ARL0固定时,q值不变,a值越大,监测速度越高,性能越好;a值固定时,q值越大,监测速度越高,性能越好。
4 结论
本文介绍了一种更具稳健性的计数型控制图,并提出了优化方案。该控制图可以应用于各种计数数据分布中,并有良好的监测性。结论考虑实际生产中样本存在的问题,本文提出的控制图用来监控过程均值的偏移,并给出了EWMA控制图中的最优决策变量和性能指标,仿真结果表明,该控制图可以应用于各种计数数据分布中,并有良好的监测性。针对不同的均值偏移大小,质量工程师们需要选择控制图的最优决策变量,可以更快速的检测到过程中的均值偏移,减少不合格品的产生。以上研究均假设过程均值和方差已知,如果当过程均值和方差未知时,此控制图的性能需要进一步研究。
参考文献:
[1]Sheu, S. H., Lin, T. C. (2003). The generally weighted moving average control chart for detecting small shifts in the process mean[J]. Qual. Eng. 16:209-231.
[2]Khoo, M.B.C.(2004). Poisson moving average vs. c chart for nonconformities[J]. Qual. Eng. 16:525-534.
[3]Shey-Huei Sheu & Wen-Chih Chiu.(2007).Poisson GWMA Control Chart[J]. Communications in Statistics—Simulation and Computation. 36:5, 1099-1114.
[4]N. Chakraborty, S.W. Human & N. Balakrishnan (2017). A generally weighted moving average chart for time between events, Communications in Statistics - Simulation and Computation, 46:10, 7790-7817.
[5]Shin-Li Lu(2017). Optimization Problems and Methods in Quality Control and Improvement,Quality and Reliability Engineering International, 33(8), 2397- 2408.
[6]Niladri Chakraborty, Schalk W. Human & Narayanaswamy Balakrishnan (2018)A generally weighted moving average exceedance chart, Journal of Statistical Computation and Simulation, 88:9, 1759-1781.
[7]Saghir, A., Ahmad, L., Aslam, M., & Jun, C.-H. (2018). A EWMA control chart based on an auxiliary variable and repetitive sampling for monitoring process location. Communications in Statistics-Simulation and Computation, 64(9-12),1625-1642.

