重复测量方差分析的数据检验在植物生长调节剂研究中的应用及程序实现

王鑫靓

摘 要：该文结合植物生长调节剂对草坪草生长的影响试验结果，阐述了在重复测量实验的方差分析中对数据进行检验的重要性，并介绍了应用Python语言实现检验的方式。

关键词：植物生长调节剂;重复测量;方差分析

中图分类号 S688.4文献标识码 A文章编号 1007-7731（2020）09-0177-04

Application and Program of Repeated Measures Anova Data Test in Plant Growth Regulator Research

Wang Xinliang

（School of Statistics， Renmin University of China， Beijing 100872， China）

Abstract： Combined with the experimental example of the effect of plant growth regulators on the growth of lawn grass，thispaper expounds the importance of testing the data in the variance analysis of repeated measurement experiments，and introduces the way to implement testing in Python.

Key words： Plant growth regulator; Repeated measurement; Analysis of variance

1 引言

在科学试验中，常常会遇到对试验对象进行同一个因素不同水平的处理，并在一段时间内观察处理组与对照组的差值变化情况。这种试验通常会使用设立对照组的重复测量设计，并通过方差分析比较不同处理水平组均值的直接差异情况[1]。例如，生物试验中为了解生长调节剂在不同浓度情况下对植物生长的影响，可以使用方差分析法去解决[2]。

重复测量（Repeated Measures）设计是试验设计的一种，是指对同一研究对象的同一因变量在不同时间或场景的重复观测值，其目的是研究不同处理间是否存在显著差异，同时也可以研究处理因素和时间之间的交互效应[3]。通常重复测量设计中的研究因素分为2个部分：（1）处理因素：根据不同的处理水平分组再加上对照组（组间因素），在试验设计中将分组因素作为组间因素考虑，分组因素的不同水平可以包括对照组及进行不同处理的分组（因素水平>2）;（2）重复测量因素：根据时间进行的N次测量（组内因素），将不同测量时间作为组内因素考虑，重复测量次数>3。重复测量的数据必须满足一定的条件才可以进行方差分析，因此，在分析前需要对试验数据进行检验[4]。

数据检验是进行统计分析工作的重要前提，由此得到的结论才可靠有效。在对生物试验数据的研究分析中，方差分析法是最常用的方法之一，但数据检验的重要性往往被研究者忽视。不同的试验设计和研究目的，需要不同的统计分析方法，对于数据的假设检验也会因此而有所区别。SAS、SPSS等统计软件是很多科研人员经常使用的工具，随着大数据时代的到来以及计算机技术的不断发展，程序语言逐渐替代传统的统计软件，成为数据分析的强大工具[5]。以R语言或Python语言为例，程序语言灵活的使用形式、强大的扩展能力以及丰富的结果展现方式，都是其优势所在[6]。本文在前人研究的基础上，详细介绍了对单因素重复测量进行方差分析时所需数据检验的原理、内容和方法，并提出了应用Python语言实现数据检验的方法。

2 试验设计

在研究植物生长调节剂对草坪草生长影响的试验中，将草坪草样本随机分成3组，每组20株。第1组设为对照组，该组草坪草不进行任何试剂处理;第2组设为处理组1，该组草坪草由100mg/L防落素与50mg/L烯效唑的复配组合处理;第3组设为处理组2，该组草坪草由100mg/L防落素与300mg/L缩节胺的复配组合处理。在处理样本草坪草后的30d内，定期测量样本株高，每7d1次，共计4次。

防落素为苯酚类植物生长调节剂，主要用于防止落花、落果，抑制豆类生根，促进坐果，诱导无核果，并有催熟增长作用。烯效唑为三唑类植物生长调节剂，是赤霉酸生物合成的拮抗剂，对草本或木本的单子叶植物均有强烈的生长抑制作用，主要抑制节间细胞的伸长，产生植物生长延缓作用。药物被植物的根吸收，在植物体内进行传导，茎叶喷雾时，可向上内吸传导，但没有向下传导的作用。同时，烯效唑又是麦角甾醇生物合成抑制剂，有4种立体异构体。现已证实，E-型异构体活性最高，它们的结构与多效唑类似，只是烯效唑有碳双键，而多效唑没有，这是烯效唑比多效唑残效期短的一个原因，同時烯效唑E-型结构的活性是多效唑的10倍以上。若烯效唑的4种异构体混合在一起，则活性大大降低。缩节胺为内吸性植物生长延缓剂，能抑制细胞伸长，抑制赤霉素的生物合成，延缓营养体生长，使植株矮小化，株型紧凑，能增加叶绿素含量，提高叶片同化能力。

3 试验数据及检验

对于2因素重复测量数据，可以使用Two-way Repeated Measures Anova进行分析，但需要对数据进行以下几种假设检验，并以Python语言实现。

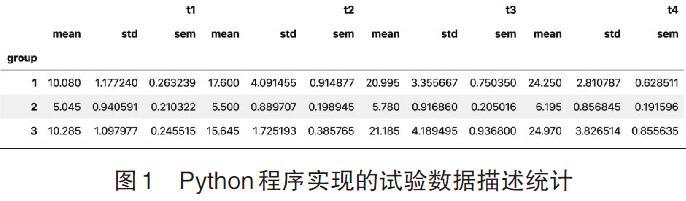
3.1 检验1：描述性统计检验 对收集到的试验数据进行初步分析，检验数据的完整性，即根据试验内容观察因变量（测量值）是否是唯一且连续变化值;组间因素的水平数（包括对照组）是否为3组;组内因素的水平数（测量次数）是否都有2个或2个以上;引例试验是否为4次。进一步查看数据的总体情况后，可通过Python程序实现数据的描述统计。确认数据的完整性后Python程序计算出4次引例试验中3组数据的均值、标准差及标准误，结果如图1所示。

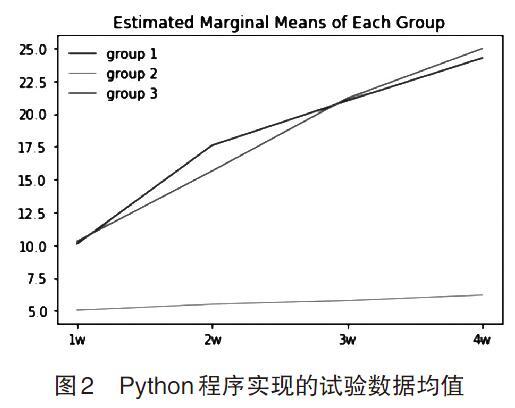
试验在不同时间点对样本进行了多次测量，可以通过绘制均值折线图描述每组数据的趋势，以初步分析数据的发展方向。通过Python程序实现的3组数据均值折线图如图2所示。由图2可知，第1组和第3组随着时间的推移，株高呈现明显的增长趋势，表明对照组和处理组2生长明显，且测量数值处于同一水平，猜测100mg/L防落素与300mg/L缩节胺的复配组合无法有效抑制草坪草的内源生长素。而第2组的生长趋势并不明显，且观察值与第1组和第3组相比少了很多，可以猜测，100mg/L防落素与50mg/L烯效唑的复配组合可以有效抑制样品的再生长。通过折线图可以对主效应和交互效应有初步的判断，但并不能因此做出差异推断，还需要对数据做进一步检验。

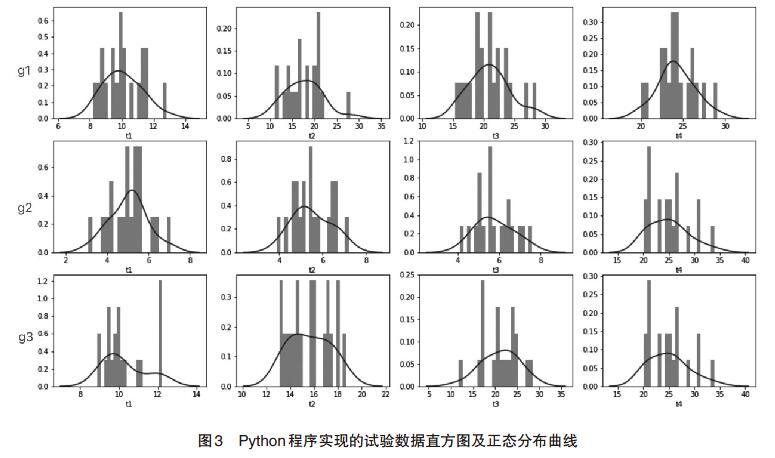
3.2 检验2：数据分布检验 各组数据之间的差异推断可通过单因素方差分析求得，进行方差分析之前需要做F分布，只有服从正态分布总体才适用于F分布的假设检验，否则，检验结果是没有意义的[7]。图示法（直方图、QQ图等）是正态分布常用的检验方法，具备简单和直观性，可采用直方图对样本测量数据进行检验，引例试验应用Python程序实现的直方图如图3所示。

除了图示法，S-W检验（Shapiro-Wilk）和K-S检验（Kolmogorov-Smirnov）也是正态分布常用的检验方法，这是比较频率分布f（x）与理论分布g（x）或者2个观测值分布的检验方法，检验功效一般随样本容量的增大而增大。S-W检验是一种基于相关性的算法，计算可得到1个相关系数，系数越接近1，表明数据和正态分布拟合得越好，适用于小样本场合（3≤n≤50）;K-S检验适用于样本量大于50的大样本场合。检验数据时通常会根据样本量的大小选择适用的检验方法，本试验中每组草坪草的样本量为20，所以选用S-W检验。计算结果返回2个值，一个是统计数（test statistic），一个是P值（p-value），如果p值小于显著性水平（P<0.05），则拒绝原假设，该分布可以认为是正态分布。引例试验各分组数据应用Python程序实现的正态检验结果如图4所示。

3.3 检验3：球性检验 在方差分析的F检验中，是以各试验组内总体方差齐性为前提的，因此，在对数据进行方差分析之前，还需对各个试验组内的总体方差先进行齐性检验。如果各个试验组内总体方差为齐性，且F检验的结果表明多个样本所属总体平均数差异显著，这时才可以将多个样本所属总体平均数的差异归因于各种试验处理的不同所致;如果各个试验组总体方差不齐，那么经过F检验所得多个样本所属总体平均数差异显著的结果，可能有一部分归因于各个试验组内总体方差不同所致[8]。

由于重复测量的试验是对同一组样本数据在不同时间点的测量，因此观察结果一般都存在一定的内相关性，由于这种内相关性不能满足一元方差分析法对独立性的要求，此时若仍然使用一元方差分析方法，会导致一类错误率增加。球形假设是利用协方差矩阵的球对称性来判断试验组内各水平的自相关程度。重复测量通常要求试验中有3次或3次以上的测量值，如果测量数据的协方差矩阵主对角线元素（即方差）相等，非主对角线元素（即协方差）为0，说明重复测量的各观测值之间没有相关性，即各变量间无关，这种情况下的数据满足球形检验的假设[9]。如果数据不能满足球性检验的假定，也可以对与时间有关的F统计量的自由度进行校正，常用的校正方法包括G-G法（Greeenhouse-Geisser）、H-F法 （Huynh-Feldt）、L-B下界法（Lower-bound）等，或不使用一元方差分析法，而改用多元方差分析方法。如果重复测量的数据之间实际上不存在相关性，则一元方差分析和多元方差分析的结果是一致的，此时称数据满足球性检验。因此球性检验是重复测量数据必要的检验步骤。

常用的球性检验方法包括巴特利特球性检验法（Bartlett′s Test of Sphericity），它是以相关系数矩阵为基础的。也就是说，巴特利特球性检验法的原假设H0为相关系数矩阵是一个单位阵，对于研究对象内因素的各个水平组合而言，即相关系数矩阵对角线的所有元素均为1，所有非对角线上的元素均为0。巴特利特球性检验法的统计量是根据相关系数矩阵的行列式得到的。如果该值较大，且其对应的相伴概率值小于指定的显著水平时，则拒绝原假设H0，表明相关系数矩阵不是单位阵，原有变量之间存在相关性;相反，则原假设H0成立，原有变量之间不存在相关性。

使用Python代码对引例试验的数据进行球性检验时，首先计算出数据帧均值的相关系数矩阵，然后再使用bartlett函数进行球性检验，得到的结果如图5所示。

Python程序计算结果显示，引例数据不满足球性检验，表明引例试验的分组因素和时间因素之间存在相关关系，即存在交互作用。这种情况下，单独分析主效应的意义不大，而应当检验处理分组的单独效应。本文引例试验中，在使用不同混合试剂对样本草进行处理后，不同的混合试剂在时间上反应出来的效应互有关联，并非独立性数据，此时，应当比较处理组和对照组在不同时间观测值的差异。

4 结论

数据检验是在进行数据分析前必不可少的步骤之一，不同的试验目的、试验设计均会影响到数据分析方法的选择。如本文试验引例中，对重复测量的数据进行方差分析时发现，数据检验的球性检验结果无法满足，此时可以在校正自由度后使用一元方差分析法，或者接受多元方差分析的结果。Python语言作为数据分析语言的代表，具有目的明确、操作简单的优势，在进行数据检验时，使用Python或其他程序语言可以更加准确有效的完成检验工作，以便进一步分析数据。

参考文献

[1]刘丽华，郭德金.方差分析中的分组比较[J].中国卫生统计，2004，21（6）：370-371.

[2]孙晓梅，张守攻，王笑山，等.生长调节剂对落叶松杂种生根和幼苗生长的影响[J].北京林业大学学报，2006，28（2）：68-72.

[3]楚洁，臧桐华，叶冬青，等.重复测量设计与随机区组设计原理及应用[J].中国卫生统计，2004，21（3）：174-175.

[4]Finney DJ. Repeated measurements：what is measured and what repeats？[J]. Statistics in medicine，1990，9（6）：639-644.

[5]Littell RC，Henry PR，Ammerman CB.Statistical analysis of repeated measures data using SAS procedures.American Society of Animal Science[J]. Journal of Animal Science，1998，76：1216-1231.

[6]肖明魁.基于python的單因素方差分析和两两比较[J].电脑知识与技术，2019（26）.

[7]刘加妹，彭景楩.生物实验数据的单因素方差分析[J].动物学杂志，2001，36（6）：34-37.

[8]潘晓平，倪宗瓒，殷菲.一种稳健的方差齐性检验方法[J].现代预防医学，2002，29：774-776.

[9]许卫华，温泽淮，王奇.重复测量资料的单独效应分析及多重比较[J].广州中医药大学学报，2017，34（5）：766-770.

（责编：张宏民）