自适应合并与分裂的多种群差分进化算法

王 浩 ，李 俊 ，周 蓉

1.武汉科技大学 计算机科学与技术学院，武汉 430065

2.智能信息处理与实时工业系统湖北省重点实验室，武汉 430065

1 引言

差分进化（Differential Evolution，DE）算法[1]是由美国学者Storn和Price等人于1995年提出的一种基于群体智能理论的优化算法。该算法通过模拟自然界“优胜劣汰，适者生存”的法则来实现种群内个体的合作与竞争，使得种群能够智能进行优化搜索。DE算法采用了变异，交叉和选择操作来实现模拟生物进化过程中的基因突变行为，将适应性最佳的个体保留下来以此寻求最优解。由于其易用性、稳健性和强大的全局寻优能力，在约束优化计算、聚类优化计算、非线性优化、控制神经网络优化等方面得到了广泛的应用。但由于差分进化是通过父代个体间的差分矢量进行变异、交叉和选择来实现寻优，与常用进化算法相类似，也存在易陷于局部最优、过早收敛和停滞的问题。

针对这些问题，国内外很多学者对DE算法进行了大量的改进，在控制参数和变异策略[2-4]的优化方面，Qin等人[5]提出了单一种群参数自适应的jDE（Differential Evolution algorithm withstrategy adaptation，jDE）。Zhang等人[6]提出了参数自适应和“current-to-pbest/1”策略的JADE（Adaptive Differential Evolution，JADE）。Wang等人提出了适合试验向量代数策略和固定参数CoDE（Differential Evolutionwith Composite trial vector，CoDE）[7]算法、变异策略和控制参数集合的EPSDE（Differential Evolutional gorithm with Ensembleof Parameters and mutation Strategies，EPSDE）[8]算法。Brest等人[9]提出了自适应DE算法SaDE，其算法根据历史经验选择成功率较高的变异策略和参数。彭虎等人[10]提出了一种新的基于三角的骨架差分进化算法（Bare-BonesDifferentialEvolution algorithm based on trigonometry，tBBDE），并使用随机泛函理论分析了算法的收敛性。算法采用了三角高斯变异策略以及三元交叉和交叉概率自适应策略对个体进行更新，并在收敛停滞时进行种群扰动。周新宇等人[11]提出了基于精英反向学习的差分进化算法。廖雄鹰等人[12]提出了基于自适应变异算子的差分进化算法。钱武文等人[13]提出了基于反射变异策略的自适应差分进化算法。在研究高效的算法架构[14-15]方面，此类优化从种群结构进行分析，将初始种群分为多个子种群，子种群间根据拓扑结构相互联系，并制订相应的个体迁移机制，形成分布式差分进化算法，分布式DE算法成为DE算法研究的重要分支，引起众多学者的关注。Tasoulis等人[16]提出了并行DE（Parallel Differential Evolution，PDE）算法，对算法的迁移策略、迁移频率、子种群数目进行了研究。王亚辉等[17]将种群分配为三个子种群，每个子种群为一种进化策略，然后根据每种策略动态地调整子种群规模。Kozlov等[18]对分布式DE算法提出了新的迁移机制，从而加快算法的收敛速度。Singh等[19]对分布式DE算法的参数、迁移周期以及迁移个体数目进行了详细的研究。DeFale等[20]采用了环形拓扑结构代替单向环的DDE算法。Weber等人[21]提出了一种缩放因子F自适应的分布式DE（“F”Adaptive Control Parallel Differential Evolution，FACPDE）。文献[22]提出了参数适应性分布式 DE（Adaptive Parameters Distributed Differential Evolution，APDDE）。

在现有研究中，DE算法仍存在收敛速度慢，容易陷入局部最优等问题，特别是在算法进化后期，种群资源分布不均、个体多样性差、算法无法跳出局部最优，很大程度地限制了DE算法的开采能力和搜索效率。针对以上问题，本文对差分进化策略、单种群进化模式两个方面进行了改进，以及加入了早熟判定，提出了自适应合并与分裂的多种群差分进化算法（Adaptive Combine and Split Multi-population Differential Evolution Algorithm，ACSMDE）。ACSMDE在进化前期很好地维持种群的多样性，保证了算法的寻优能力，同时有效地避免“陷入局部最优”，使尽可能地找到全局最优解；而在进化后期，ACSMDE能在全局最优解附近继续收敛，提高算法收敛精度。通过与其他6个具有代表性的算法在CEC201730个标准测试函数的实验结果表明，ACSMDE在算法收敛速度以及收敛精度上有较好的提升。

2 基本DE算法

DE算法是一种基于群体的全局自适应搜索优化算法[23]，进化流程与遗传算法（GA）[24]非常类似，其首先要随机初始化种群，然后借助种群个体间的差分信息对个体形成扰动进而搜索整个种群空间，最后利用贪婪机制选择下一代个体，寻求问题的最优解。差分变异、杂交、选择为DE算法的3个基本操作。最常见的差分变异策略有以下5种：

式中，为变异后的个体；为当前种群中随机选取的5个不同的个体；为当前个体；为当前全局最优个体；F为缩放因子；g为当前进化代数。

交叉作为差分变异搜索策略的一种有效补充，DE采用对于每个目标向量和其相应的变异向量进行均匀交叉，进而产生试验向量)，具体定义如下：

其中，Cr为交叉概率；jrand为[1,2,…,D] 的随机整数。

如果循环代数G超过了最大迭代次数或者精度达到要求则停止搜索，否则继续对种群执行变异、交叉和选择等操作。

3 自适应合并与分裂的多种群差分进化算法

3.1 子种群自适应组合与分裂

由于差分进化采取启发式搜索模式，种群的进化很容易被种群最优个体所操控，陷入局部最优，因此本文采用分布式差分进化算法[22，25]（DDE）架构，DDE算法开始时将种群划分为若干个子种群，在进化的过程中，每个子种群独立进化，子种群按照拓扑结构排列，使得每一个子种群只能向特定的子种群传递信息，同样，它只能从特定的子种群中接收信息。在满足给定概率的情况下，子种群间进行信息交流。从迁移种群选择最佳个体，替换掉被迁移子种群中随机挑选的一个个体，通过迁移，实现在子种群间的信息交流，此过程使得算法很好地从不同子种群的多样性中收益，图1为环形拓扑结构的迁移过程。

图1 环形拓扑迁移过程

DDE算法在算法前期很好地实现多种群间的信息交流，但是这种某子种群最优个体替换另一子种群的随机个体的操作，使得最后子种群的最优个体趋于统一，种群多样性降低，大量的种群资源不能得到有效的利用，在算法后期仍然不好解决陷入局部最优问题，因此本文提出了子种群自适应合并与分裂的策略，其子种群间的具体操作步骤如下：

步骤1设置一个最大子种群数pmax和最小子种群数pmin，在初始化种群过程中，将种群平均分配pmax个子种群，并为每个子种群设置一个种群优劣因子，来表示种群优劣性。

步骤2通过计算各个子种群的个体适应度值fit，找到全局最优个体及所在的子种群k，通过式（8）、（9）来更新各个子种群的种群优劣因子：

在算法迭代过程中，每一个子种群代表着一个小区域，子种群的优劣性会根据各个子种群中最优个体的适应度值进行比较，但是最优子种群的最优个体可能为局部最优，而全局最优个体可能存在另一个子种群所在区域内，只是还未探寻到，但传统多种群DE算法[26]随着子种群间的交流迭代最后种群趋于统一，多样性降低的同时也陷入局部最优，本文提出子种群优劣因子，在算法迭代过程中，子种群不会立即进行子种群间的交流，而是添加了一个阈值，当子种群的种群优劣因子达到此阈值时，才进行交流，让每个子种群有一定的时间在自己所属的区域内进行迭代寻优，保证个体多样性的同时也有效防止陷入局部最优。

在初始化时设置各个子种群的种群优劣因子为0；step设置为25；Dr设置为0.6。从式子可以看出，在每一次迭代更新过程中，只有拥有全局最优个体的子种群，其种群优劣因子才会增加，其他不包含全局最优个体的子种群的种群优劣因子会减少，当其减少为0或者小于0时则重新设置为0。

步骤3通过迭代更新后的子种群的种群优劣因子来判断是否进行种群间的组合和分裂，如果满足要求则进行组合或分裂操作。在算法迭代初期，为了保证个体尽可能存在于存在的极值点的区域内，需充分发挥算法的全局搜索能力来保证种群的多样性和公平竞争性，故采取随机平均分配种群个体，并设置种群数量相对较大，设为10。在算法迭代后期，为了尽可能地增强局部寻优能力，能够在当前区域内寻求到最优解，此时需将更多的个体资源用于提供给较优子种群，从而使其在最优值附近的小区域内进行探索，增强算法的开发能力，故一些种群优劣因子较小的子种群会被淘汰掉，将其种群资源合并到最优子种群，此时子种数会减少，但是为了避免最优子种群的最优解为局部最优解，故最小子种群数不能设为1，为了增强算法跳出局部最优能力，本算法将最小子种群个数设为4。

步骤4更新组合或者分裂后各个子种群的个体及相关数据，子种群交流结束。

组合就是在所有子种群中选出种群优劣因子最小的子种群，将其种群资源全部重新分配给种群优劣因子最大的子种群的过程，如图2，在初始化时设置所有子种群规模因子sizek=1，当某个子种群的种群优劣因子到达某个阈值T且子种群的数目不小于最小子种群数目Pmin时执行组合操作，从式（8）可知，只有拥有全局最优个体的子种群的种群优劣因子才会增加，所以每次执行组合操作只会合并最优子种群与最劣子种群，子种群个数P将会减少1，子种群将会被消除，并将其种群资源通过式（10）重新分配给子种群，得到合并的子种群的子种群规模因子通过式子（公式（11））来更新。

为最佳子种群的最优个体，为最佳子种群的两个随机个体。

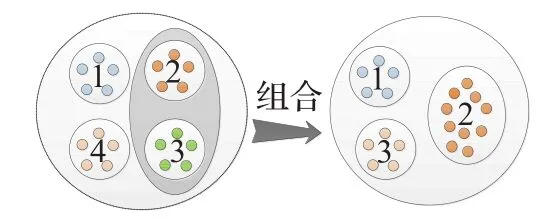
图2 子种群组合过程

分裂就是在种群迭代过程中通过判断子种群的种群优劣因子，若其等于0且种群规模因子sizek>1，则表示此种群占据太多资源但是不能寻找到更优的个体，所以会将其分裂并重新初始化。其分裂过程如图3所示，根据此种群的种群规模因子sizek将其重新平均分配为sizek个子种群，所有种群的个体通过式（12）进行初始化。

图3 种群分裂过程

3.2 精英池学习

在每一次迭代过程中，经过变异交叉后产生新的个体，根据适应度值进行优劣比较，获胜的进入下一代进行新的迭代，同时该获胜个体和所对应的缩放因子、交叉因子加入到当前子种群的精英池中，也就是说精英池用来保存每次迭代获胜的个体以及所对应的缩放因子和交叉因子。在算法进化初期，随着迭代次数的增加，精英池中存放的个体以及参数会随之增加，但由于更早进入池内的信息会随着代数的增加其对种群的价值会减少，针对此问题设置精英池容量Tank，并根据先进先出原则，当加入的信息溢出精英池时算法选择移除最早加入的精英信息。

个体的多样性主要由多种群的拓扑结构来保证，在每一个子种群内部，更多强调的是到达极值点的寻优能力，精英池只需保存最新产生的较优个体即可，而无需保存较早产生的个体，同时为了减少冗余使算法性能更优，本文将精英池规模设为当前子种群的1/2，初始化时精英池为空。若算法在解决复杂多峰问题时，需要更多的个体信息来增加开采能力，建议适当扩充精英池的容量甚至可以等同于当前种群规模。

标准差分进化算法的变异策略都会从当前种群中随机选择个体，以及约定好的缩放因子和交叉因子来进行变异和交叉。此算法对变异策略做了改进，种群通过在精英池中选择优良个体参与变异策略和更新缩放因子和交叉因子，通过式（13）、（14）进行变异策略，在精英池中分别产生服从正态分布的CRi和服从柯西分布的Fi来更新种群的缩放因子和交叉因子。

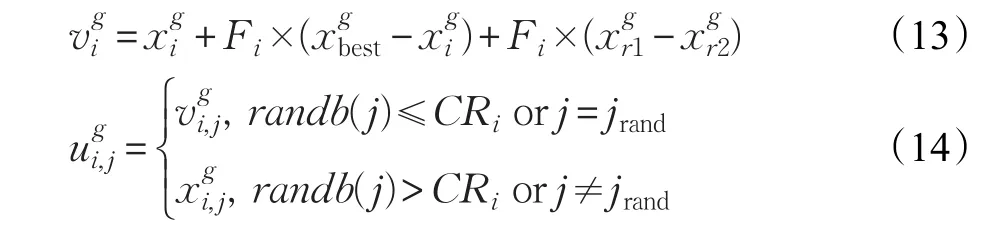
为变异后个体；为当前个体；Fi为当前个体对应的缩放因子；为精英池中选择的个体；为当前种群随机选择的个体为在交叉选择过程中的选择的第j维；CRi为当前个体对应的交叉因子；jrand为随机选择的变异维。

3.3 早熟判定及变异策略

在DE算法后期，产生早熟收敛的根本原因是随着迭代次数的增加和种群多样性的快速下降，个体间适应性的差异性越来越小，形成了个体聚集，陷入局部最优，从而难以收敛到更好的解。针对此问题，ACSMDE提出了早熟判定以及相应的变异策略。通过式（15）进行种群早熟判定：

其中，ε为早熟检验阈值，为第g代和第g+P代种群的最优个体的适应度值，本文中取P=100，ε=1E−6。算法每迭代P次后，进行一次早熟判定，若第g代和第g+P代种群的最优个体的适应度值的差值小于ε，表示算法陷入了局部最优或者搜索处于停滞状态。因为DE算法的本身局限性，在解决多峰问题时就很容易进入此状态，所以在DE算法中进行早熟判定具有很强的普适性[27]，即从迭代开始就进行早熟判定。当种群满足式（15）时表示种群陷入局部最优，则对最佳个体进行个体变异，本文选择拉格朗日插值法进行变异策略，其一般形式运用方法为：在平面上有(x0,y0),(x1,y1),…,(xn-1,yn-1)共n个点，xi为自变量的取值，yi为对应函数的取值，任意的两个xi互不相等，集合Bk是关于点(x,y)的集合，Bk={0,1,…,n-1}，对于任意的k∈Bk，都有lk(x)，Bk={i|i≠k,i∈Dn}使得：

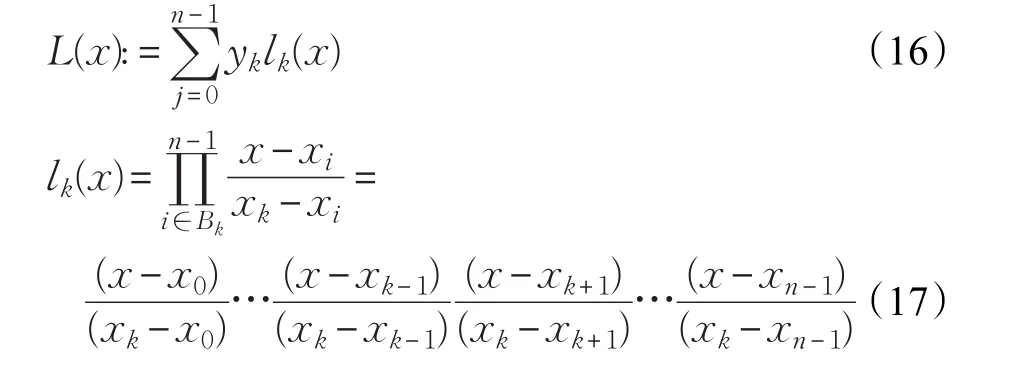
函数L(x)的图像经过这n个点，也就是说拉格朗日插值法可以给出一个恰好穿过二维平面上n个已知点的n-1次多项式函数（17），式（18）为n=3时的多项式函数。

(4)在最佳挡板高度的前提下，调节风门开度，使得炉排横向配风更均匀，其最佳风门开度(从风室进口到尾部)依次为100%、70%、50%、50%、50%，其配风不均匀系数为7%。

算法的变异策略如下：在当前种群的最优个体上选取某一维，希望通过拉格朗日插值构造出一个多项式函数，通过多项式函数来找到在此维度上适应度值最大的值。因为算法每次只在一个维度上的最优点进行变异，所以只需在此维度上产生两个临近值，用这两个值分别替换掉原来的值后计算适应度，由此又生出了两个点，将生成的两点和原来的点代入式（18）产生一个二次项函数，根据二项式函数的函数性质，当其最高项的系数不为零时为一个一元二次函数，当其最高项的系数为零时为一次函数，在根据其几何性质选取变异点。具体过程如下：找到在此当前种群最优个体为[xbest,1,xbest,2,…,xbest,D]，选取第j维并计算其两个邻近值，其计算式如下：

其中，Rj为在第j维上搜索范围，rand（0，1）为（0，1）内的随机数，N为种群个体数目。

将分别用和替换，得到两个新的个体x1、x2，计算三个个体的适应度值并按从小到大排序，依次记为，对应的三个点x0()、)、x2()，将这三个点代入拉格朗日插值公式（18）可得一个关于x的方程：

由平面几何知识以及二次函数极限的定义可知，在一个可导点的两侧各取一个相对靠近的点，其几何关系只能存在图4中四种情况，分析满足此条件三个点的几何意义，如图4所示。

图4 参数a与b不同取值下的

当a=0,b=0时，其几何图形如图4中的（1）所示，表示这三个点在一条平行于横坐标的直线上，取xmin～xmax中的任意一点。

当a=0，b≠0时，其集合图形如图4中的（2）所示，表示这三个点在一条倾斜的直线上，即为在范围内随机取的一个点。当a>0时，其集合图形如图4中的（3）所示，表示这三个点在一开口向上的抛物线上，取值为。

当a<0时，其集合图形如图4中的（4）所示，表示这三个点在一开口向下的抛物线上，若在对称轴左侧，即为在xmin～范围内随机取的一个点；若在对称轴右侧即为在～xmax范围内随机取的一个点。

将xbest的第j维用替代，得到新的个体[xbest,1,…,…,xbest,D]，计算x3的适应度值fit3通过式（27）进行更新种群。

最优个体依次从维度1到D进行拉格朗日更新，直到找到最优个体或者到达最高维为止。

3.4 算法实现过程

步骤1设置参数和初始化子种群以及初始化子种群优劣因子。设置最大子种群个数pmax，最小子种群个数pmin，初始子种群规模N，子种群合并阀值Tmax和子种群分裂阀值Tmin，子种群交流概率E1，种群更新系数Up和Dr，子种群规模因子SIZE，缩放因子最大值Fmax和最小值Fmin，交叉概率因子最大值Crmax和最小值Crmin，变量的上下界xmax与xmin变量维数D，种群最大进化代数Gmax，早熟控制周期P，早熟检验阀值ε。用式（12）来初始化各个子种群，计算出各子种群个体的适应度值，找到各个子种群适应度最优的个体xbest及对应的最佳适应值fitbest，并将各个子种群的种群优劣因子Fitg置为0，进化代数置为0，初始缩放因子和交叉概率因子都置为0.5。

步骤2变异交叉以及选择操作。本文使用式（13）的差分策略实现个体变异，式（14）实现交叉操作，通过比较原始个体与交叉操作后的个体的适应度值，选取较佳个体作为下一代的个体实现选择操作。

步骤3子种群间的合并与分裂。各个子种群先进行个体评价，找到最优个体来更新子种群优劣因子，通过子种群优劣因子来进行子种群间的合并与分裂。

步骤4更新精英池。在各个子种群中，将步骤3中寻找到较佳个体添加到精英池，并判断精英池是否溢出，当总个数超出精英池容量时剔除较早进入精英池中的祖代个体，并通过新的精英池来更新缩放因子和交叉变异因子。

步骤5早熟判定。如果判定为早熟则使用拉格朗日插值法进行变异策略。

步骤6判断是否到达最大迭代代数，如果是，算法结束，否则跳回步骤2。

4 函数仿真与分析

4.1 参数设置

ACSMDE算法的各项参数设置：在低维D=30情况下种群规模NP=150，最大演化代数Gmax=3 000；在高维D=100情况下NP=250，最大演化代数Gmax=5 000。

为了全面客观地对ACSMDE算法进行评价，本文将其与标准DE[1]算法（DE/rand/1）以及研究人员近些年提出的优秀算法JDE[5]、tBBDE[10]、RDE[28]、AM_DEGL[29]、APPDDE[22]在收敛精度，收敛速度以及时间复杂度上进行比较，各算法均独立运行20次。其他比较算法的参数设置均与原文献一致。实验环境为：处理器Intel®Core™ i5-7200U CPU@2.5 GHz RAM 4 GB，Win10 64位操作系统，MATLABR2016a。

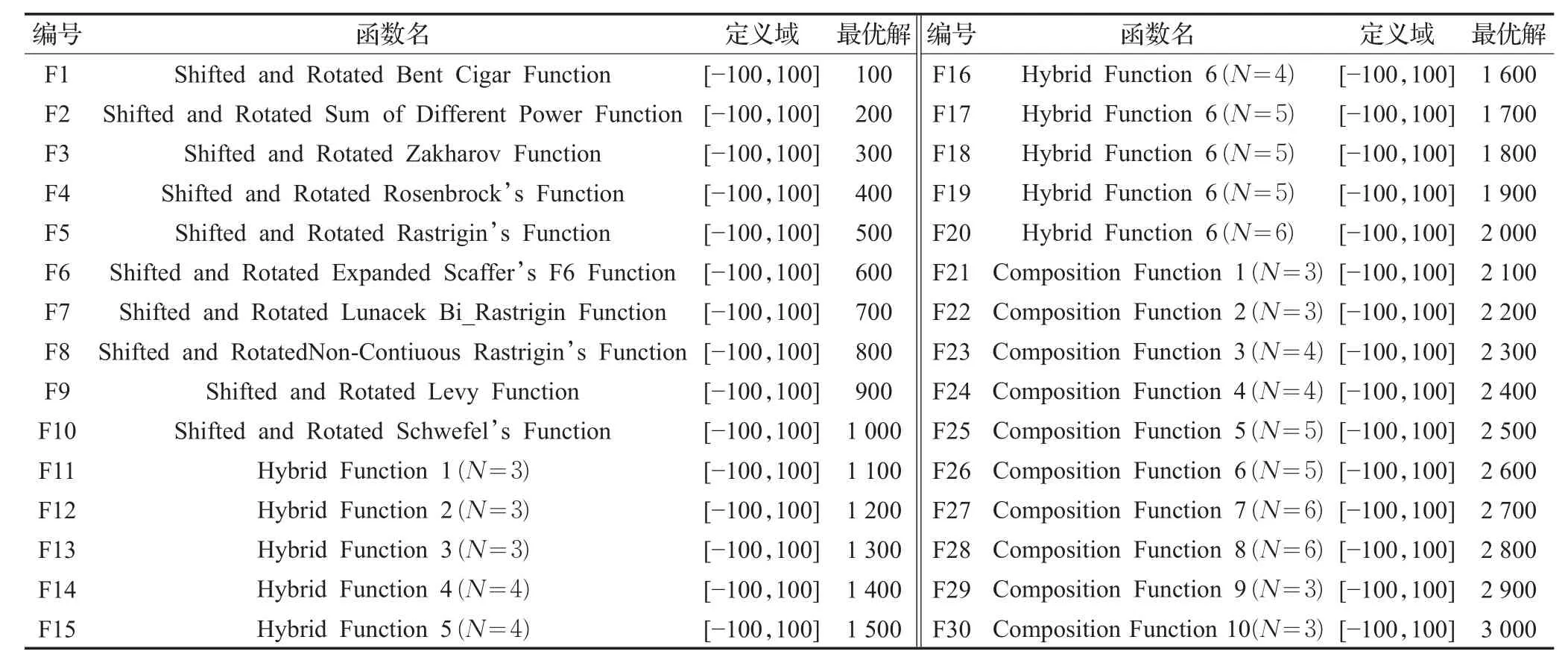
表1 标准测试函数

4.2 测试函数

为了测试本文算法的可行性，选择CEC2017[30-31]中的30个标准测试函数，具体定义如表1所示，其中，F1、F2、F3为单峰函数，F4～F10为简单多峰函数，F11～F20为混合函数，F21～F30为复合函数。

4.3 实验结果与分析

4.3.1 算法收敛精度分析

在表2、表3的数据中存在数据相同但并未加粗的情况，是因为数据在使用科学计数法进行数学统计时，四舍五入会使得很邻近的数据最后表示出来为相等数据，但实际上未加粗数据的真实值是略大于加粗数的真实值的，同时，在表2、表3中存在平均值同时加粗的情况，是因为对应算法都能达到测试函数的全局最优点或局部最优点。

表2为各算法在低维(D=30)情况下的平均值，方差的实验对比结果，其中最好结果已加粗标出。从平均值指标来看，对于F2、F3、F4、F5、F7、F12、F16、F19、F23、F27等9个测试函数，ACSMDE均达到了最优精度，无论是简单函数，多峰函数，还是复合函数，混合函数都能够在指定约束条件下达到最优，并且在其他测试函数F8、F13、F14、F20、F25、F26上仍然具有较好的精度，与对比算法中最优结果相差结果不大，说明ACSMDE算法具有较强的精度探索能力。并且在测试函数F2、F3、F4、F12、F19上，ACSMDE均达到各个测试函数理想的最优解，说明ACSMDE的具有很强的探索开采能力，同时，ACSMDE在测试函数F2、F3、F4、F17的方差指标上也能达到最小，在算法稳定性上也有一定的保证。

表3为D=100的情况下各算法的平均值和方差实验对比结果，其中最好数据已加粗标出。从表中的数据可以看出，当维度D=100时，从平均指标来看，对于F1、F2、F3、F4、F5、F11、F17、F18、F19、F20、F21、F23等12个测试函数，ACSMDE算法在精度排名上均排名第一。同时ACSMDE算法在测试函数F7、F11、F13、F26、F29等与最佳算法最优值差距不是特别明显，并且在较少的迭代次数上能够稳定地收敛到全局最优，同时对比表2和表3，随着问题维度的增加，ACSMDE算法搜索性能的优势进一步体现出来，无论是收敛精度还是收敛的稳定性在对比算法中有较大优势。综上所述，无论是在低维D=30还是在高维D=100，ACSMDE算法在与其他6个对比算法中均能取得较明显的优势，这说明自适应合并与分裂的种群结构，精英池学习以及早熟判定及变异策略确实能提高算法的寻优能力以及寻优精度。

表2 ACSMDE与其他算法的比较(D=30)

表3 ACSMDE与其他算法的比较(D=100)

4.3.2 算法收敛速度分析

为了进一步分析ACSMDE算法在不同函数上的收敛速度，分别进行了在不同维度（D=30和D=100）下30个测试函数与其他几个DE算法的比较实验。实验结果表明：在其他算法的收敛速度受到高纬度的限制时，ACSMDE算法无论是高维还是低维，在大多数函数上的收敛速度较之其他算法更快，都具有较高的收敛性能。图5给出了D=30和D=100时各算法在测试函数上的收敛曲线，其中lg表示以10为底的对数（限于篇幅，每种维度只给出具有代表性的3个函数）。

由图5可知，当D=30时，对应图中的（a）、（b）、（c），函数F5、F16、F22都能快速收敛，并且在算法后期同其对比实验算法相比达到更好的精度。特别是测试函数F5和F16，在保证算法快速收敛的同时也有高质量的解。当D=100 时，对应图中的（d）、（e）、（f），对于函数F1、F11、F17，ACSMDE在收敛性能够很好地超越其他算法，并能搜索高质量的最优解，对于F1和F17，算法不仅在前期与其他一些算法相当，并且在其他算法都达到收敛时，仍具有继续寻求最优解的能力，在能快速收敛的同时也有很好的收敛精度。

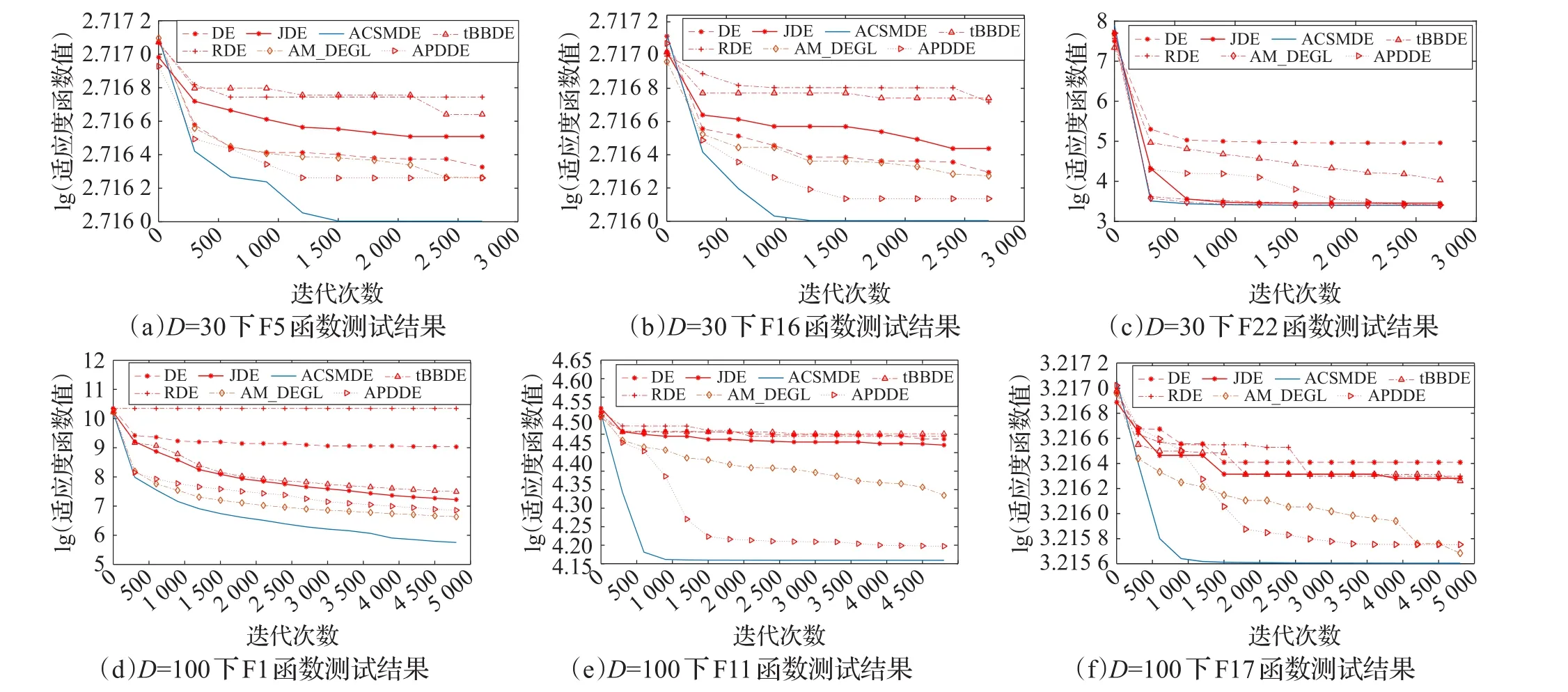
图5 算法的收敛性比较

4.3.3 算法复杂度分析

通过对算法实现步骤来分析ACSMDE的时间复杂度，其中种群规模为NP，问题维度为D，迭代次数为T。算法步骤1初始化种群时间复杂度为O(NP⋅D)，步骤2变异交叉操作为O(NP⋅D)，步骤3选择操作为O(NP)，步骤4合并与分裂子种群更新为O(1)，更新精英池（池子规模为O(NP)数量级）操作有从池顶加入新的精英个体以及池底移除祖代精英个体，其时间复杂度为O(NP⋅D)，早熟判定为O(1)，综上所述，ACSMDE算法的总时间复杂度为O(NP⋅D⋅T)，仅与NP、D和T有关，ACSMDE算法与标准DE算法时间复杂度一致，对算法的改进没有增加过多的计算开销。

总结以上实验分析发现，虽然ACSMDE算法在极少数函数的性能不佳，但对于绝大多数测试函数而言，基于自适应合并与分裂的种群结构，精英池学习，早熟判定及变异策略较大地提高了的DE算法收敛速度和收敛精度，同其他6种算法相比，ACSMDE算法的优化性能具有很大的优势，且稳定性更佳。

5 结语

本文提出了自适应合并与分裂的多种群差分进化算法ACSMDE，算法将种群分为多个子种群，在算法迭代初期，子种群个数较多，子种群间通过种群优劣因子来进行交流，保证种群多样性和个体多样性，有效加强DE算法的全局寻优能力和避免陷入局部最优能力；在每个子种群内部，采取了精英池学习的策略来保存较优个体和对参数进行动态更新，使算法在较优个体的附近继续进化，易于求得较好的解，极大地提高了算法的局部寻优能力。并设置了最小子种群数和种群早熟检测及变异策略，增强跳出局部最优的能力，同时也提高了算法的精度，通过对CEC2017的30个测试函数与几个有代表性的DE算法的对比实验，证明了本算法的适用性、有效性和准确性。