水下机械手电液伺服系统前馈补偿控制策略研究

王鸿飞，严 允，罗凌波，晏红文

（上海中车艾森迪海洋装备有限公司，上海 201306）

0 引言

机械手是作业级水下机器人最重要的作业工具之一，它不仅可以直接进行水下作业，还可操纵其他水下作业工具，从而协助完成水下样品采集、化学物理探测、水下打捞和装卸、水下电缆和管道铺设、军事布雷等多种民事和军事任务，其性能直接影响整个水下作业系统的实际工作性能。按驱动方式，机械手可分为电机驱动式和液压驱动式两类。目前大部分作业级水下机器人均采用液压驱动的方式；电机驱动式机械手虽然近年来也在快速发展，且在浅水和轻载场合已得到越来越多的应用，但在深水和重载作业场合，液压驱动式机械手更具竞争优势，短时间内仍无法被替代。

作业级水下机器人一般携带两个机械手，常见的配置是一个锚定机械手加一个高性能灵巧机械手。锚定机械手出力较大，用来夹持在水下基础上从而固定和稳定机器人的位置姿态，一般采用开关控制方式，对精度没有严格要求，结构和控制简单；高性能灵巧机械手通常有6个运动自由度，外加一个作业工具或夹持器，业界称之为七功能机械手，其常采用电液伺服控制方式，对稳态、动态控制性能要求较高。

电液伺服系统被广泛应用于航空航天、武器系统、船舶海工、机床、冶金、锻压和大型装备试验系统等领域，其主要特点如下：液压执行机构的功率-质量比（或转矩-惯量比）大，因此电液控制系统加速性好、结构紧凑、尺寸小、质量轻；电液控制系统刚度大（即输出位移受外负载的影响小）、定位精确，所以位置误差小、精度高；液压系统散热更方便，因为液压油是很好的载热介质，可以把系统中因功率损耗产生的热量通过管路分散到别处。这些特点使得电液伺服系统非常适合应用于体积和重量受限、控制性能要求高的水下机器人，但其具有很强的非线性且数学模型很难被精确建立，因此系统的控制实现较为复杂。为此，本文针对水下机械手的工作特点，以Titan 4水下机械手为例，进行电液伺服系统建模仿真研究并提出相应控制策略。

1 水下机械手系统结构组成与工作原理

目前业内所应用的高性能水下机械手一般为七功能位置控制机械手，其以高可靠性和灵敏性著称[1]，如Schilling公司Titan系列产品。图1所示为Titan 4水下机械手，其是一种结构紧凑、负载能力大、作业范围宽、操纵灵活、控制精度高的七功能机械手，采用主从位置伺服控制方式。

图1 Titan 4水下机械手Fig. 1 Titan-4 underwater manipulator

由于大部分的水下工作任务是针对海底或机器人前方垂直平台进行的，所以业内标准的机械臂被设计成反铲式（即肘部在上的结构形式），这样能使工作空间最大化、结构体积最小化。表1示出Titan 4机械手主要参数。

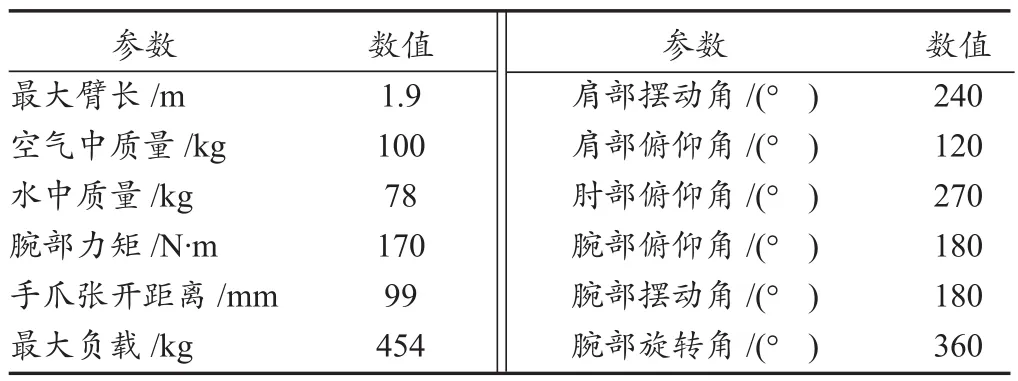
表1 Titan 4机械手主要参数[1]Tab.1 Main parameters of the Titan-4 manipulator [1]

1.1 水下机械手系统结构

Titan 4水下机械手系统[1]主要由主手控制器、从手、补偿器及管路线缆等组成（图2），可以直接由水下机器人本体的液压源对其供能。通过主手控制器发出指令信号来控制从手进行操作，主手的每个关节控制从手的相应关节。

图2 Titan 4水下机械手系统组成Fig. 2 System composition of Titan-4 underwater manipulator

机械手本体结构功能主要包括肩部摆动、肩部俯仰、肘部俯仰、腕部俯仰、腕部摆动和腕部旋转6个自由度功能以及一个夹持功能（图3）。

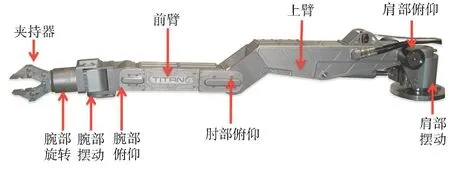
图3 Titan 4水下机械手结构组成Fig. 3 Structure composition of Titan-4 underwater manipulator

从驱动系统执行机构的结构形式来看，肩部俯仰和夹持功能是伺服阀控非对称液压缸，腕部旋转是伺服阀控摆线马达，肩部摆动、肘部俯仰、腕部俯仰和腕部摆动是伺服阀控摆动对称液压缸（图4）。

阀控摆线马达和阀控摆动缸可通过物理符号变换，等效转化为阀控对称液压缸的形式，所以此水下机械手执行机构可被简化为阀控对称液压缸和阀控非对称液压缸两种结构形式（图5），两种形式的基本控制原理是相同的。本文以阀控对称液压缸为研究对象进行分析。

1.2 电液伺服系统的闭环控制原理

电液伺服系统的闭环控制原理如图6所示。主手控制器发出的每个关节位置指令信号与从手对应关节的液压缸的位移输出反馈信号构成位置闭环。指令信号与反馈信号作差后经控制器调节产生对伺服阀的驱动信号，驱动信号由D/A板卡采集、转换后，经信号调理电路和功率放大器产生电流信号来驱动伺服阀运动。伺服阀根据电流驱动信号的变化来控制液压油的流量，从而控制液压缸按照指令信号运动。系统的位移反馈信号由安装在液压缸上的位移传感器测量，并经A/D板卡转换为数字信号后输入数字控制器[2]。

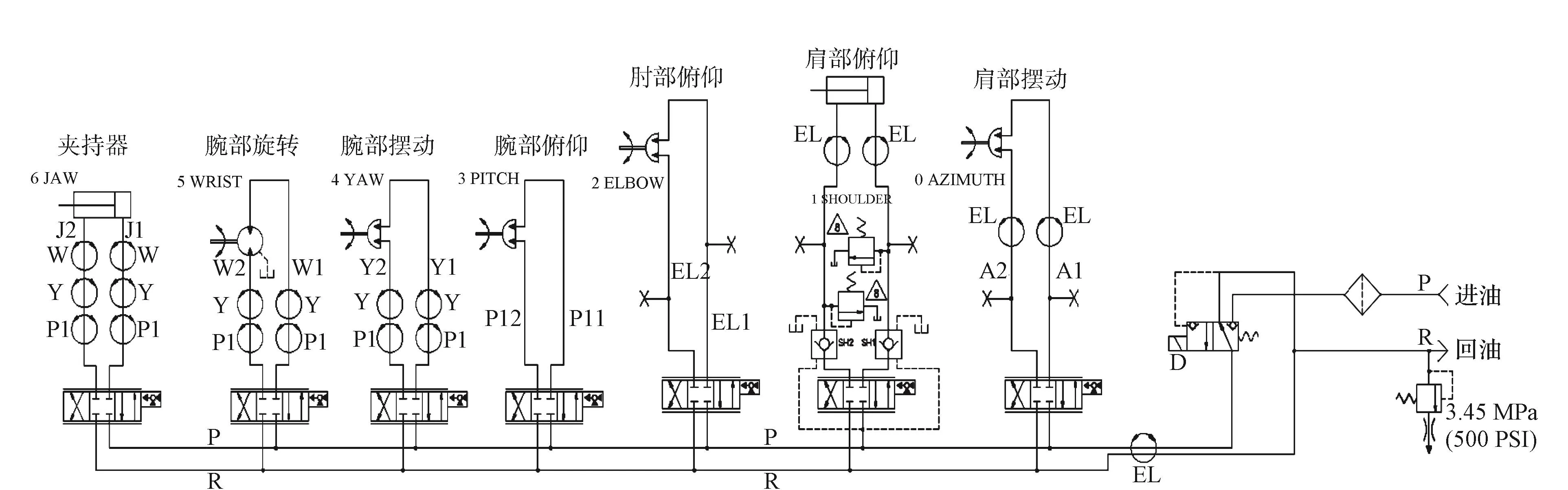
图4 Titan 4水下机械手液压原理[1]Fig. 4 Hydraulic schematic diagram of Titan-4 underwater manipulator [1]

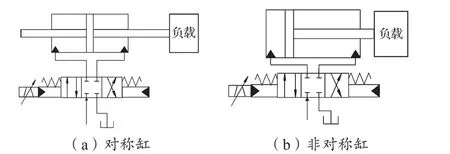
图5 阀控对称缸与阀控非对称缸Fig. 5 Valve-controlled symmetrical cylinder and valvecontrolled asymmetrical cylinder

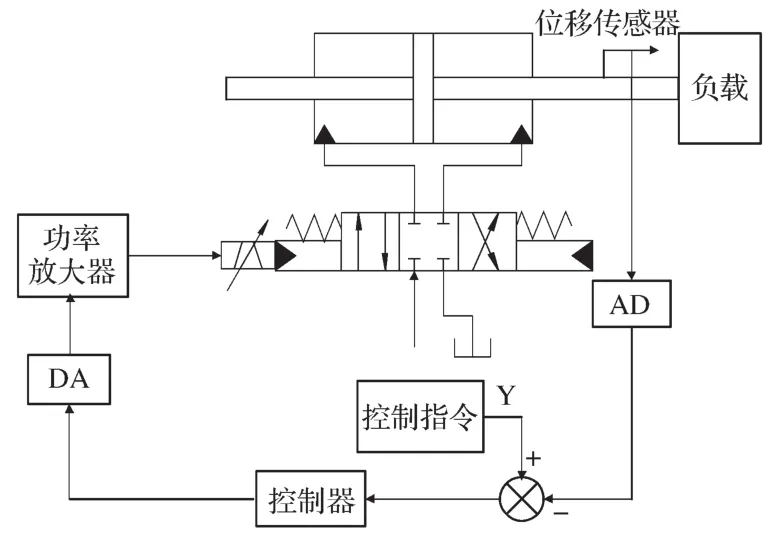
图6 电液伺服系统闭环控制原理Fig. 6 Principle of the closed-loop control for electro-hydraulic servo system

2 电液伺服系统数学建模

本文将对电液伺服系统的伺服阀和液压动力机构分别建立数学模型，为后续使用时域和频域法分析系统动态特性建立依据。

2.1 液压动力机构建模

伺服阀控对称液压缸的动力机构原理如图7所示。液压动力机构由四边滑阀和液压缸组成。滑阀是转换放大元件，它将输入的阀芯位移信号转换成液压信号（流量、压力）输出，并加以功率放大。液压缸是执行元件，其输入是压力油的流量，输出是运动速度（或位移）。滑阀阀体与液压缸缸体刚性联结在一起，构成反馈回路[5]。

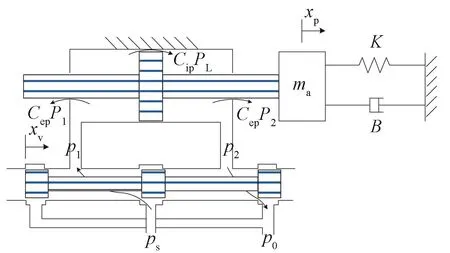
图7 伺服阀控对称液压缸动力机构原理Fig. 7 Principle of servo valve controlled symmetrical cylinder power mechanism

其基本方程涉及伺服阀滑阀流量、液压缸流量连续性、液压缸和负载的力平衡[3]，具体分别如式（1）～ 式（3）所示。

式中：qL——伺服阀的负载流量，m3/s；Kq——伺服阀的流量增益，(m3/s)/mm；Kc——流量-压力系数，(m3/s)/Pa；xv——阀芯位移，mm；pL——液压缸的负载压降，Pa。

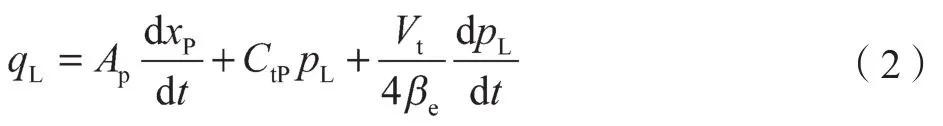
式中：Ap——液压缸活塞有效面积，m2；xp——活塞杆位移，m；Ctp——液压缸总的泄漏系数，(m3/s)/Pa；Vt——液压缸的总压缩体积，m3；βe——液压油的有效弹性模量。

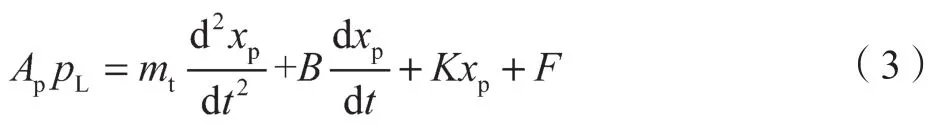
式中：mt——活塞和负载的总质量，kg；B——活塞和负载的黏性阻尼系数，N/(m·s-1)；K——负载的弹簧刚度，N/m；F——作用在活塞上的任意外力，N。

对式(1)～式(3)进行拉氏变换，可得液压动力机构控制原理，如图8所示，其中Qv为液压动力机构输入，Xp为该机构输出。

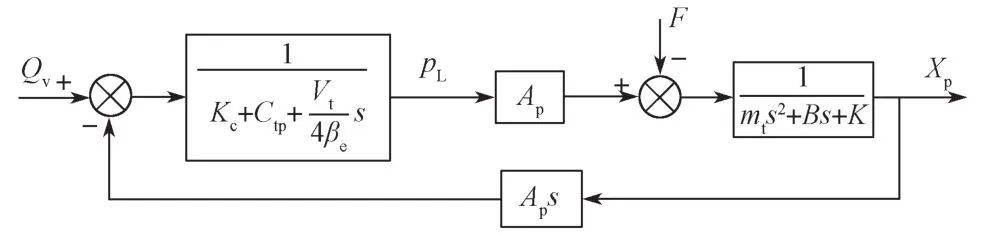
图8 伺服阀控对称液压缸动力机构控制原理Fig. 8 Power mechanism principle of servo valve controlled symmetrical cylinder

对于位置控制伺服系统，其主要负载为惯性负载 。为简化分析，本文忽略其黏性阻尼B和负载刚度K，并令外力F=0。由图8可得动力机构输入（Qv）和输出（Xp）的传递函数：

2.2 伺服阀建模

从控制的角度，伺服阀本身便是一个复杂的闭环系统，典型二级伺服阀的原理见图9。图中，K1为力矩马达增益，(N·m)/mA；K2为液压放大流量增益，(m3/s)/m；K3为滑阀流量增益，(m3/s)/m；Kw为反馈刚度，(N·m)/m；Kf为挡板的静刚度，(N·m)/m；A为滑阀作用面积，m2；ωsv为伺服阀一阶自然频率，rad/s；δsv为伺服阀一阶阻尼系数；I为伺服阀输入电流，A。

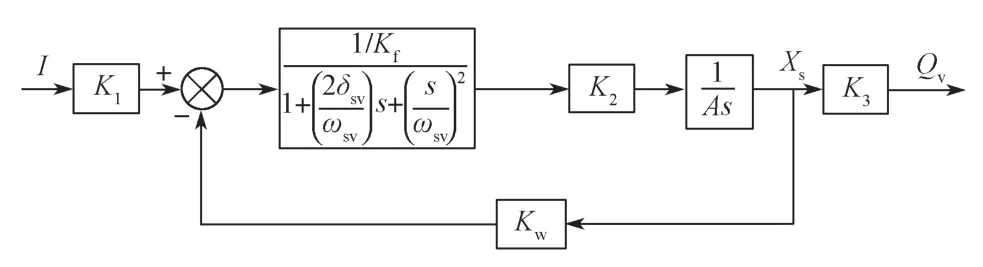
图9 伺服阀系统原理Fig.9 Schematic diagram of servo valve system

经过简化后的伺服阀传递函数仍可能高于二阶，但根据实测的动态特性曲线，起主导作用的是一对复数极点。从实用角度出发，工程上一般用传递函数来描述流量伺服阀特性：

式中：Ksv——伺服阀增益，m3/(s·A)。

Titan 4机械手采用Moog公司30系列军用标准伺服阀，其一阶固有频率达到814 Hz，远大于液压动力机构的固有频率，伺服阀最高响应频率达到200 Hz。因此该系统中伺服阀对系统动态性能的影响较小，可将式（5）简化为比例放大环节：

3 控制器设计与系统仿真研究

水下作业环境的多变性、水动力对潜水器本体与机械手运动的影响以及本体与机械手的运动耦合都使机械手的控制更具有挑战性，从手相对主手的跟随精度和响应速度直接影响到潜水器水下作业的性能和效果，因此，高精度和高响应的控制性能是主从控制的高性能机械手的重要指标。

对电液伺服系统而言，由于很难获得某些参数的精确值，如泄漏系数、黏性阻尼系数及压力流量系数等，故只能根据经验确定一个相对准确的估计值；而系统工作过程中存在很大的非线性，体积弹性模量、介质黏度、阻尼比等参数会随着压力、温度及阀开度的变化而变化，因此，很难建立精确的电液伺服系统数学模型。在系统建模时，一般会进行一些假设，忽略某些次要因素并对系统进行线性化处理，在此基础上进行控制算法设计，可取得一定的控制效果；但当系统的工作点在大范围内变化时，非线性带来的影响就会变大，此时线性模型就不再适用，因此电液伺服系统不易实现复杂的控制算法。

工程上应用较多的PID控制算法并不要求精确的被控对象数学模型就可在一定程度上达到较高的控制精度和良好的跟踪效果，因此，对机械手的各关节伺服系统来说，PID仍是首选的基本控制策略之一[4]。但对传统的PID控制算法而言，由于其不依赖于被控对象精确的数据模型，所以很难同时兼顾控制精度和控制速度。为满足机械手高精度和高响应的要求，需对系统进行补偿，以在保证精度和稳定性的前提下提高系统响应。基于此，本文在伺服系统PID控制的基础上，采用极点配置的方法对系统进行前馈补偿控制，以增加系统响应带宽，提高系统响应速度。

3.1 PID控制

PID控制是工业界技术最成熟也最常用的控制方法，其参数整定方便、易于实现、控制效果显著。PID控制器的控制律为

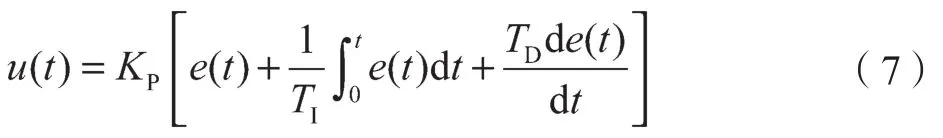
式中：KP——比例系数；TI——积分时间常数；TD——微分时间常数；e(t)——输入。

为了验证控制策略的有效性，利用Matlab/Simulink工具，构造电液位置伺服系统模型，并采用PID控制器进行仿真。当指令输入为20 mm、等效负载为50 kg时，系统的阶跃响应曲线和Bode图如图10所示，其上升时间约为0.1 s，稳定时间约为0.5 s，幅频响应-3 dB时频率约为3.25 Hz，带宽较低。

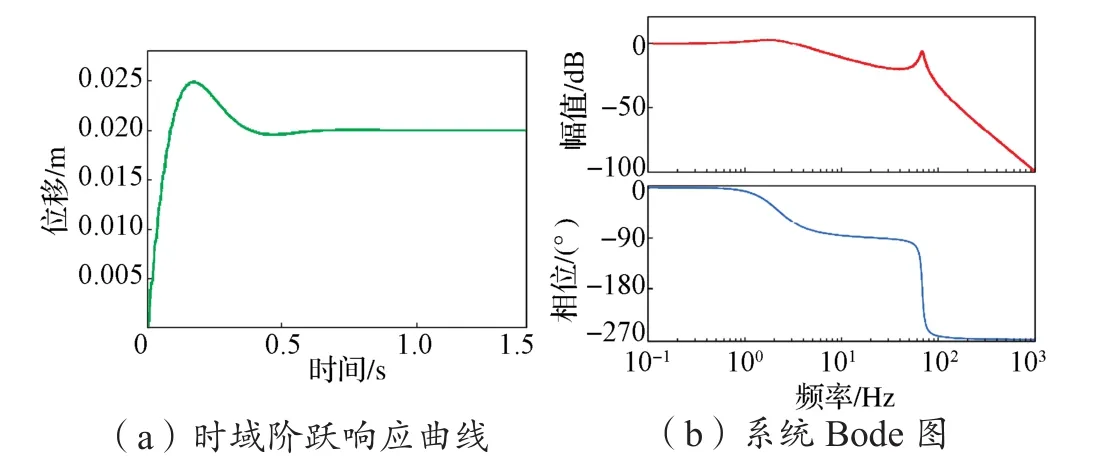
图10 PID控制阶跃响应输出曲线与Bode图Fig. 10 Output curve and Bode diagram of PID control step response

从Bode图中看出，系统在68 Hz左右（即液压固有频率处）有一个谐振峰，降低了系统幅值裕量。若要在不降低系统快速响应能力的前提下提高系统幅值裕量，或在不降低幅值裕量的前提下提高系统快速响应能力，需要提高系统阻尼比。

3.2 前馈补偿控制

由上述分析可知，液压动力机构的阻尼很小，使用PID方法进行控制时系统带宽较低，若要增加系统带宽，可使用极点配置的方法对系统进行补偿；但由于液压位置伺服系统的阻尼较小，其幅频特性在液压固有频率处有谐振峰，影响系统的稳定性，还需要设计结构滤波器来抵消谐振峰的影响。为此，本文借鉴在地震模拟振动台伺服控制系统中广泛应用的三状态控制技术[5]对机械手伺服系统进行控制。

地震模拟振动台要求具有较高的响应带宽和足够的稳定裕量，普遍采用的控制方法是三状态控制（包括三状态反馈和三状态前馈2个控制环节，见图11），应用极点配置原理对系统闭环极点进行重新配置，实现系统带宽的扩展和系统稳定性的提高。三状态是指加速度、速度和位移3种参量。一般振动台都需要采集负载的加速度和位移信号同时合成等效的速度信号，从而实现对系统的三状态控制。控制环节中，三状态前馈用来对消系统传递函数距离虚轴较近的极点以拓展带宽，三状态反馈则在位置闭环的基础上提高液压动力机构的阻尼比和液压固有频率[6]。但对于机械手伺服系统，由于只能得到其位移信号，因此无法进行三状态反馈控制。三状态前馈其实是一种前馈补偿控制技术，其作用是对消系统闭环传递函数靠近虚轴的极点：当系统具有二阶振荡特性时，对消其二阶振荡因子；当系统具有一阶惯性特性时，对消其一阶惯性因子[6-7]。因此，可以将三状态控制技术的前馈控制方法应用到机械手伺服系统中。

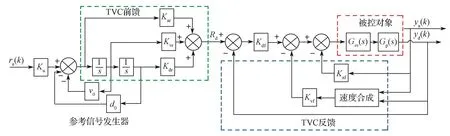
图11 三状态控制器原理图Fig. 11 Schematic diagram of the 3-state controller

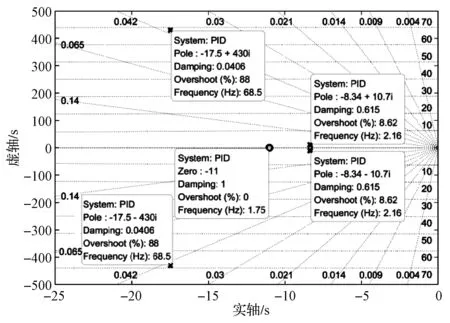
图12 PID控制闭环系统零极点图Fig. 12 Zero-pole diagram of closed-loop PID control system

图12 示出PID控制的闭环系统零极点图。可以看出，在2.16 Hz和68.5 Hz处有两对极点，其中2.16 Hz处极点距虚轴较近，对系统响应影响较大，本文将采用极点配置方法消除其影响；68.5 Hz即为液压系统固有频率，该处的阻尼系数较小（只有0.04），使系统幅频响应受到谐振影响，而该谐振与负载有关，故本文使用结构滤波器来消除其影响。

令三状态前馈控制器为

式中：Kdr——三状态前馈位移增益；Kvr——三状态前馈速度增益；Kar——三状态前馈加速度增益。

根据零极点分布图，加入三状态前馈控制，抵消2.16 Hz处的共轭极点。经仿真，系统Bode图如图13所示，可以看出，由于系统谐振的存在，系统是不稳定的。由于此谐振与系统负载相关，可使用结构滤波器消除其影响。

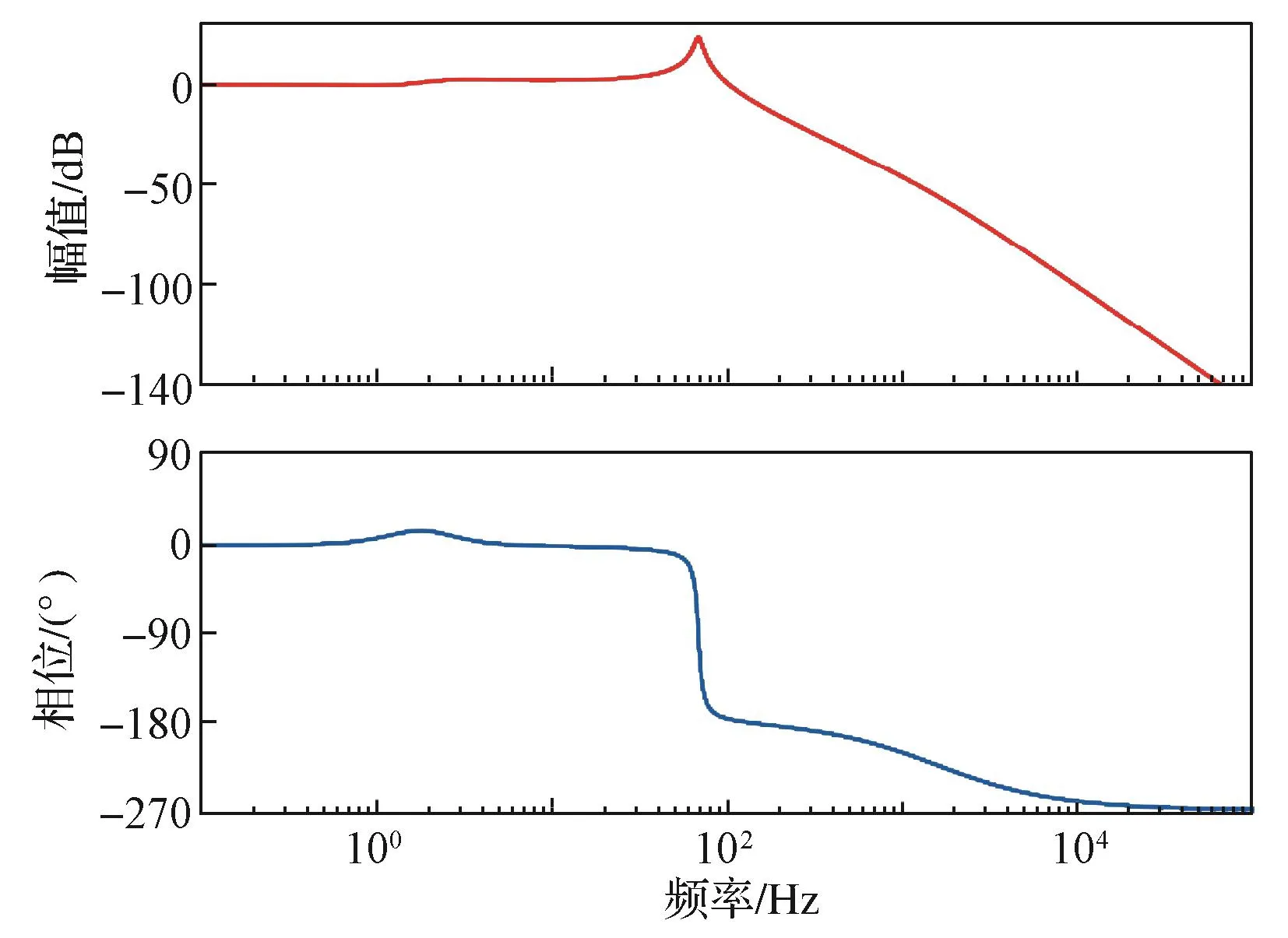
图13 加入前馈控制后系统的Bode图Fig. 13 Bode diagram of the system with feedforward control

3.3 结构滤波器

结构滤波器具有很深的零点，可通过设计滤波器的中心频率和深度来抵消系统出现的谐振峰[8-10]。本文根据伺服系统出现的谐振峰特性设计了一个简单的离线结构滤波器，以对系统进行补偿。

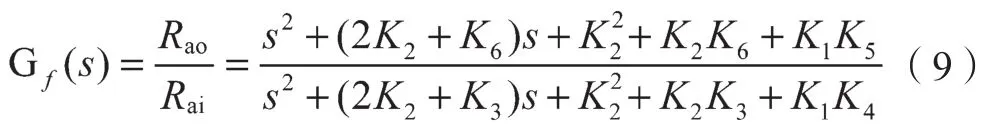
式中：K1——调节中心频率的参数；K2——调节宽度的参数；K3——调节深度的参数；K4——调节低频幅值的参数；K5——调节高频幅值的参数；K6——调节深度的参数，作用与K3相反；Rai——滤波器输入；Rao——滤波器输出。

设计了一个中心频率为68.5 Hz、深度为-21 dB的结构滤波器，其参数如表2所示，滤波器的频率特性如图14所示。

表2 结构滤波器参数Tab. 2 Structure filter parameters

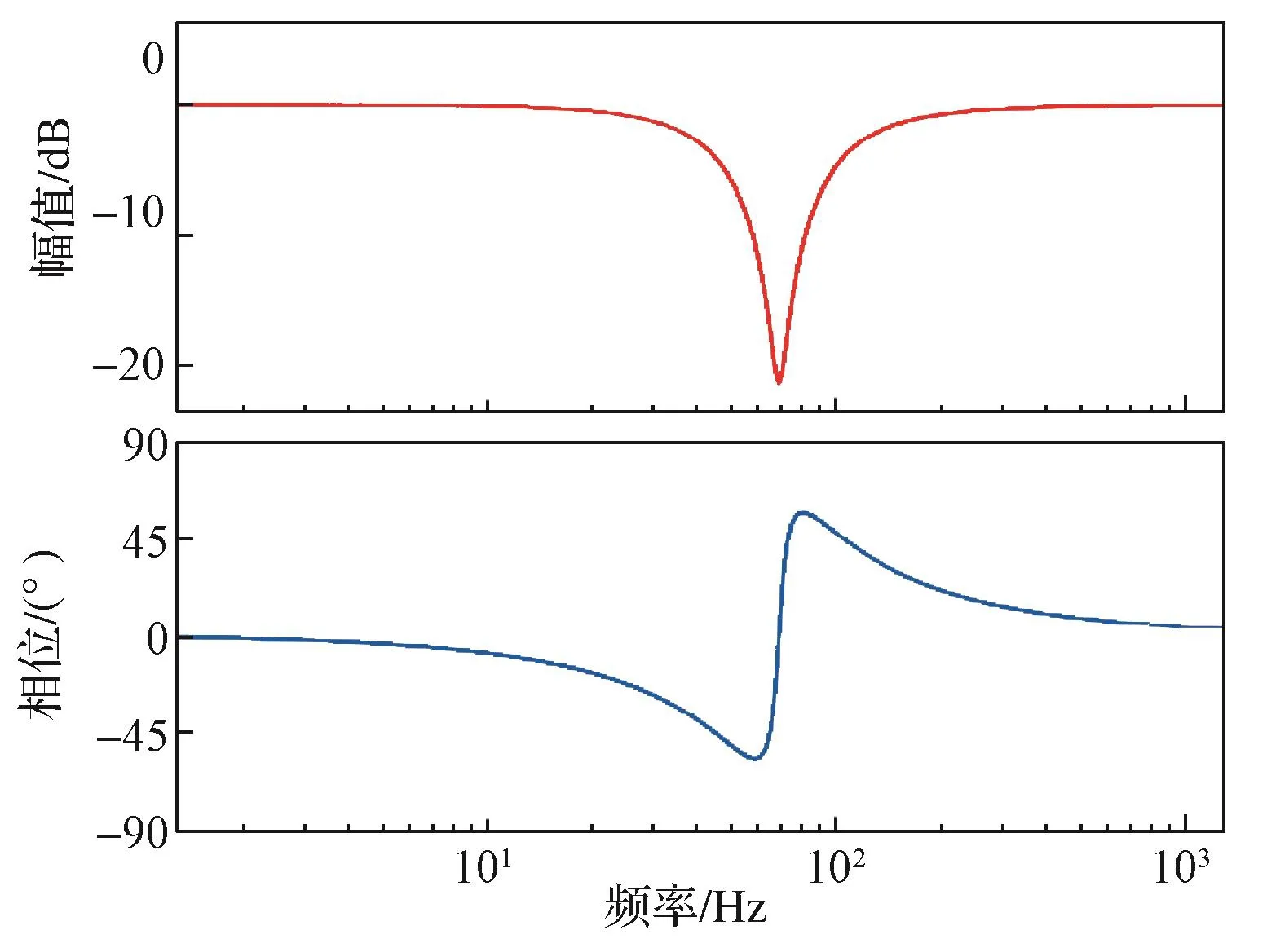
图14 结构滤波器Bode图Fig. 14 Bode diagram of structure filter

在系统前馈控制环节中加入结构滤波器，经仿真，可得系统阶跃响应曲线和Bode图（图15）。当指令输入为20 mm，等效负载为50 kg时，其上升时间约为0.05 s，稳定时间约为0.15 s，幅频响应-3 dB时频率约为83 Hz。与未加前馈补偿控制前的系统响应比较，控制性能得到很大的提升（表3）。

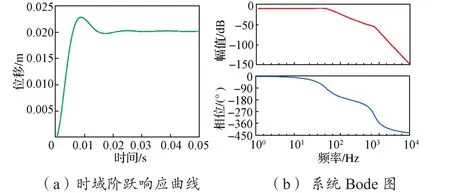
图15 加入结构滤波器后系统阶跃响应曲线和Bode图Fig. 15 Stepped response curve and Bode diagram of the system with structure filter

表3 系统性能比较Tab. 3 System performance comparison

需要注意的是，由于系统谐振与负载相关，本文所使用的离线结构滤波器只有针对特定的负载特性时才会取得良好的效果；当负载尤其是质量变化时，本文的结构滤波器将不再适用。因此，在设计结构滤波器时，要根据机械手最大额定负载进行设计，使结构滤波器适用于更大的负载范围。另外，还需对水下机械手的典型负载进行进一步的统计研究，以指导控制策略设计。

4 结语

由于水下作业环境恶劣、工况复杂、不确定因素多，要求水下机械手具有响应快、精度高等特点，对机械手伺服系统采用传统的PID控制不易取得较满意的控制效果，研究更先进、更实用的控制策略对提升水下机械手的工作性能具有重要意义。本文对水下机械手的电液伺服系统进行分析建模，根据地震模拟振动台常用的三状态控制技术，设计了一种前馈补偿控制器，取得了很好的控制效果，并通过仿真进行了验证。

无论是液压驱动还是电机驱动，对伺服系统来说只是其驱动方式不同，其基本的伺服控制原理是相同的。本文对典型的液压驱动机械手的伺服系统控制策略进行了分析，相应思路可推广至电动伺服系统控制策略的设计，为将来进行液压或电机驱动水下机械手的研发建立了理论基础。